圆筒形FPSO干拖运动特性计算研究

王家乐 吕津波 周 燕 孔德宇

（海洋石油工程股份有限公司，天津 300451）

0 引言

随着油气资源的开发逐渐向深远海迈进，海洋工程技术也随之高速发展，不仅在实际工程中得到应用的浮式海洋平台的种类越来越多，而且浮式平台的尺度与自重也越来越大。这就使浮式海洋平台的拖航过程得到了越来越多的关注与重视。浮式海洋平台的拖航一般分为干拖与湿拖2 种类型。其中，湿拖是浮式平台在自身浮力作用下浮于水中并由多艘拖轮进行拖航；干拖则是将浮式平台整体装载到大型驳船上，再由大型驳船运载到指定地点卸载。由于干拖对运输驳船要求较高，因此国内对干拖运输的研究在最近几年才逐渐增多。魏佳广等[1]与杨光等[2]利用MOSES软件对使用半潜驳船对张力腿平台进行干拖运输的完整稳性与破舱稳性进行了计算校核；吴波等[3]与李军等[4]基于波浪势流理论对大型结构物干拖运输中的运动响应和加速度进行了数值计算分析；于常宝等[5]以某大型FPSO 为例，对比了干拖、湿拖2 种方案下的总纵强度、稳性等关键考量点。该文以目前新兴的圆筒形FPSO为例，通过数值计算，在时域中分析了其在干拖运输过程中的运动特性，并与湿拖方案中的运动结果进行了对比和分析。

1 计算方法

1.1 数值计算模型

该文的研究内容为某圆筒形FPSO 平台的干拖过程，并以装载完成FPSO 的某半潜驳船为研究对象。其船体的主尺度参数见表1，同时将固连在一起的FPSO 和半潜驳船视作一个整体，其质量模型的相关参数见表2。

表2 FPSO 与驳船整体参数

通过数值分析软件MOSES 建立用于计算的圆筒形FPSO 及驳船的整体数值模型，如图1 所示。

图1 FPSO 及半潜驳船的数值计算模型

1.2 载荷及运动响应计算

针对干拖过程中的FPSO 平台与半潜驳船的整体模型，主要考虑波浪载荷与风载荷2 种环境载荷。其中，波浪载荷基于三维势流理论与面元模型。使用面元法这种常用于分析大型结构物的波浪载荷与运动响应的数值方法来进行求解，这也是进行数值模拟时的MOSES 软件的基本理论。

风载荷对整体模型的作用力矩则通过常用的近似公式来得到，如公式（1）所示。

式中：Mw为风载荷对整体模型的作用力矩；Cm为相应的风载荷系数，根据高度系数与形状系数确定；ρ为空气密度；V为流体速度；L为特征长度。

将整体模型视为刚体，其在环境载荷作用下运动的刚体运动方程如公式（2）所示。

式中：η为刚体的运动响应；[M]为刚体质量矩阵；[B]为黏性阻尼矩阵；[K]为刚度矩阵；Fwave为整体模型所受的波浪载荷；Fwind为整体模型所受的风载荷；Fg为整体模型自身重力。

基于三维势流理论与面元理论求解该方程，即可得到计算模型各自由度的运动响应结果。

2 干拖运动特性计算

针对FPSO 干拖整体模型在拖航过程中的运动特性，该文通过数值模拟对其各自由度运动进行了计算。首先计算了0°（随浪）至180°（迎浪）内各浪向上整体模型各自由度运动的RAO（幅值响应算子）。在对FPSO 本身及整体模型稳性的影响相对更大的垂荡、横摇与纵摇运动中，垂荡与横摇运动的极值出现在90°（横浪）工况，完全符合理论预期；纵摇运动的极值则出现在迎浪与随浪附近区间的多个浪向上，与常规船体RAO 结果不同。同时得到整体模型垂荡运动的固有周期为12s，横摇运动的固有周期为12.5s，纵摇运动的固有周期为15s。

然后在频域计算结果的基础上继续进行时域中各自由度运动极值的统计与分析。在时域模拟中，FPSO 干拖整体模型同时受到波浪载荷与风载荷的影响，该文根据其在拖航过程中会遭遇的实际海况进行了设置，即波浪谱选取γ=1.0 的Jonswap 谱，有义波高为4.89m，谱峰周期为9.97s，浪向为0°～180°，间隔22.5°；风谱选择NPD 谱，风向与浪向相同，将海拔10m 处1h 的风速设为17.7m/s。

应用上述工况参数计算9 个风浪同向的工况，每次模拟计算时长为3h。同时，为了分析运动响应对波浪谱峰周期Tp的敏感性，在其余参数不变的情况下增设了Tp=8.0s与Tp=12.1s 这2 个不同谱峰周期的时域计算工况。整体模型部分运动响应的时域计算结果统计值如图2 所示，图2统计的是多次计算的极值平均值。

图2 运动响应时域计算结果

根据图2 可以发现，垂荡与横摇运动的极值出现在浪向为90°（横浪）的工况，随着浪向角向0°（迎浪）或180°（随浪）变化，运动幅度逐渐变小，符合理论预期情况。通过不同谱峰周期下运动响应极值的对比可以发现，在其余参数不变的情况下，该FPSO 干拖整体模型的运动响应随着谱峰周期Tp的增加，其幅值明显增大，说明具有较高的敏感性。但同时也可以发现，随着Tp的增加，运动响应增加幅度逐渐变小，说明运动响应对谱峰周期的敏感性并非线性，谱峰周期越大，运动响应对其的敏感性就越弱。

运动加速度时域计算结果如图3 所示。图3 中的水平加速度是沿x轴加速度与沿y轴加速度的合加速度。同时需要注意的是图3 展示的加速度计算结果是FPSO 重心处的加速度，而非整体模型重心处的加速度。如图3 所示，水平加速度与垂向加速度都在横浪（90°）工况下出现最大值，而对比不同的谱峰周期可以发现，随着谱峰周期的增加，运动加速度的增加幅度逐渐变小，Tp=12.1s 工况下2种方向的加速度结果比Tp=9.97s 工况下增加的量极小，这说明运动加速度对谱峰周期的敏感性以比运动响应更快的速率逐渐降低，并在Tp=12.1s 时达到极限，运动加速度基本不再随谱峰周期的增加而增大。

图3 运动加速度时域计算结果

综上所述，圆筒形FPSO 干拖方案的运动特性主要受运输驳船船型的影响，FPSO 本身只是一种装载工况，其本身特点基本不会对运动产生影响，这也是干拖方案与湿拖方案的不同之处。

3 与湿拖运动性能对比

对于FPSO 的运输，除了上述的干拖方案，还可以采用湿拖方案，即FPSO 平台直接下水并通过多个拖轮牵引进行拖航。干拖方案应用较早、技术相对成熟，而湿拖方案流程更简单，在工程上两者各具优势。2 种方案在运动特性上存在的差别主要源于湿表面形状的不同：干拖方案中主要为驳船船型，湿拖方案中则为平台自身。为了研究2种不同拖航方案的适用性，该文针对同一个圆筒形FPSO，将2 种方案中的FPSO 运动性能进行了对比。

湿拖方案中FPSO 运动性能的计算是通过商业软件ANSYS-AQWA 进行的，完成圆筒形FPSO 数值模型的建立后，在与干拖方案相同参数的计算工况下进行了时域模拟，并统计了各浪向下运动响应及加速度的极值。将干拖方案中FPSO 的运动响应与湿拖方案的计算结果进行对比，部分对比结果如图4 所示。

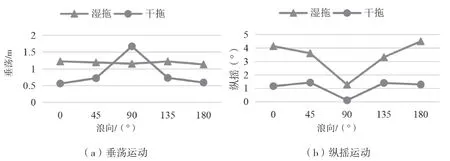
图4 2 种拖航方案的运动响应对比

在垂荡运动极值的对比结果中，湿拖工况下各浪向垂荡运动极值近似相等，这是因为圆筒形船体是对称的，所以垂荡运动大小与浪向无关；干拖工况大部分浪向下的垂荡运动极值低于湿拖工况，只是在接近90°浪向的小部分区间内会超过湿拖工况。对于纵摇与横摇运动极值的计算结果，湿拖工况下的圆筒形FPSO 由于相对于X轴和Y轴皆对称，因此横摇运动结果与纵摇类似，只是最大值出现的浪向相差90°；而干拖工况下，由于驳船在纵向上的尺度较大，因此纵摇运动在各浪向下的运动极值均小于湿拖工况且差距显著。

2 种拖航方案船体加速度对比如图5 所示。图5 中的水平加速度同样是FPSO 重心处沿X 轴加速度与沿Y 轴加速度的合加速度。可以看到，由于圆筒形FPSO 的对称性，因此湿拖工况下水平加速度与垂向加速度极值大小均与浪向无关；而在干拖工况中，水平加速度与垂向加速度均在90°浪向（横浪）下出现最大值。对比可以发现，在绝大部分浪向下，干拖工况的水平加速度远小于湿拖工况，仅在横浪周围的小范围区间内略微超过湿拖工况；而干拖工况的垂向加速度超过湿拖工况的浪向区间较大，且在横浪下更是显著大于湿拖工况。

图5 2 种拖航方案船体加速度对比

综上所述，干拖工况下FPSO 的运动性能在大部分情况下优于湿拖工况，从运动性能方面考虑，该文建议圆筒形FPSO 的拖航使用干拖方案，但在干拖中需要根据环境因素进行合理规划，尽量避免出现横浪工况。

4 结论

该文首先对某圆筒形FPSO 在干拖过程中的运动响应进行了模拟计算，并根据计算结果研究了其运动特性；其次对比了干拖、湿拖2 种拖航方案下该FPSO 的运动性能。经过上述研究，可以得出如下结论：1）FPSO 干拖过程中的垂荡运动与横摇运动极值均出现在横浪工况。2）FPSO干拖过程中的运动响应对波浪谱峰周期的变化比较敏感，而运动加速度对谱峰周期的敏感性较低。3）FPSO 干拖方案的运动性能比湿拖方案更优，但拖航过程中应避免出现横浪工况。