基于改进型偏最小二乘法的谐波源识别
2023-06-07张建明赵巧玲贾远温
张建明 赵巧玲 贾远温
(1.兰州倚能电力设计咨询有限公司,甘肃 兰州 730050;2.兰州资源环境职业技术大学,甘肃 兰州 730030)
0 引言
由于各种非线性负荷大量应用到实际生产中,因此一次谐波也日益凸显。谐波不仅会导致用电设备发生故障,而且还会影响整个电网的运行情况。
谐波源识别主要有2 种方法:1) 基于谐波状态估计法[1]。它可以通过计算系统各节点谐波电压及支路谐波电流来判断谐波源的位置。2) 将供电系统等效成系统U(Utility)和用户C(Customer),由相应等效电路模型确定谐波源的位置[2]。为了准确识别系统中各个谐波源,该文利用改进型偏最小二乘法[3]进行研究,用估计值代替实际测量值,同时结合阻抗法,通过谐波电流的大小来判断主要谐波源,从而识别谐波源的位置。
1 改进型偏最小二乘法原理
由等效电路模型确定谐波源的方法主要包括功功率法[4]、无功功率法[5-8]以及线性回归法[9-11]等。当采用传统的偏最小二乘法时,有可能出现遗漏一些成分的情况,这些成分可以很好地反应响应变量,从而使回归结果存在较大误差。因此,需要对其进行改进,即采用正交投影法消除解释矩阵中与响应变量没有统计学意义的信息。经过改进后,解释矩阵中的信息就全部与响应变量有统计学意义了,可以达到偏最小二乘回归法的要求,再采用该方法进行相应变换。实施方法如下 :1) 解出矩阵的全部特征值,解得q-1 个正交特征向量a1、a2、...、aq-1,这些特征向量与全部特征值0 有统计学意义。2) 得到矩阵BTXTXB的q-1 个特征值λ1、λ2、...、λq-1,同时得到各个特征值所对应的标准特征向量α1、α2、...、αq-1,再筛选相对较大的m个α1、α2、...、αm,使它们的和在所有特征值之和中占较大的比重。3) 设C=XBA,矩阵A=(α1、α2、...、αm),那么C就是要采用正交投影法去除的成分。4) 在C上对解释矩阵X进行投影处理,就可以得到公式(1),X0可以采用偏最小二乘法对因变量矩阵Y进行回归计算。5) 采用偏最小二乘法使Y对X0进行回归计算,得到Y1=X0、α=Xβ,那么β便是采用改进型偏最小二乘法对X进行回归所得的系数。
式中:B为回归系数的估计量;X为自变量矩阵;D为回归系数;Pc为回归系数矩阵;Ip为解释矩阵。
2 谐波源识别的基本原理
如果要识别系统中的谐波源,就要比较在公共耦合点处流向系统侧谐波电流与流向负荷侧谐波电流的大小。当从系统侧流出的谐波电流大于从负荷侧流出的谐波电流时,说明系统侧是主谐波源,反之就说明负荷侧是主谐波源。该文采用改进型偏最小二乘法对谐波阻抗进行估算,用估算得到的谐波阻抗判断谐波源电压或电流的大小,从而得到主要的谐波源。系统等效电路如图1 所示。
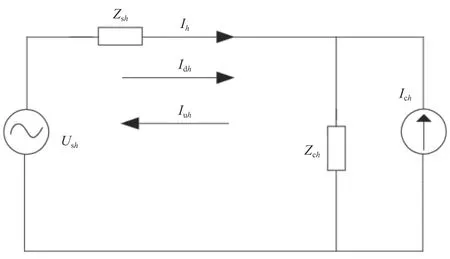
图1 系统等效电路图
由图1 可知,从负荷侧流出的h次谐波电流Iuh如公式(2)所示。
从供电端流出的h次谐波电流Idh如公式(3)所示。
比较Idh和Iuh的大小可以确定主谐波源。因为无法直接测量阻抗,所以该文采用改进型偏最小二乘法估算谐波阻抗。
改进型偏最小二乘回归法的主要内容如下:经测量得到公共耦合点的谐波电压信号、谐波电流信号,再通过测量值评估谐波阻抗和谐波电压的大小。
谐波源检测模型如图2 所示,根据模型电路图就可以得出相应的方程,如公式(4)所示。
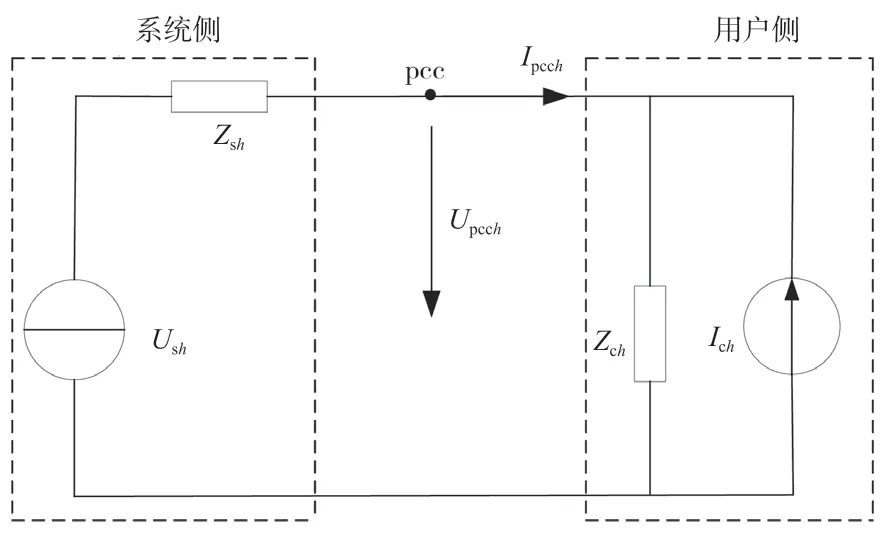
图2 谐波源检测模型
将公式(4)的实部和虚部展开就有公式(5)、公式(6)。
式中:Ushx为系统侧的h次谐波电压源的实部;Ushy为系统侧的h次谐波电压源的虚部;Upcchx为公共耦合点的h次谐波电压的实部;Upcchy为公共耦合点的h次谐波电压的虚部;Ipcchx为公共耦合点的h次次谐波电流的实部;Ipcchy为公共耦合点的h次次谐波电流的虚部;Zshx为系统侧的h次谐波阻抗的实部;Zshy为系统侧的h次谐波阻抗的虚部。
利用改进型偏最小二乘法对公式(5)、公式(6)进行回归计算就可以得到回归系数Ushx、Ushy、Zshx和Zshy,再根据回归系数求得系统谐波阻抗的平均值,如公式(7)所示。
式中:n为分段数;Zshxi为第i段系统侧h次谐波阻抗的实部;Zshyi为第i段谐波阻抗的虚部。
系统背景谐波电压平均值如公式(8)所示。
式中:Ushxi为第i段系统侧h次谐波电压源的实部;Ushyi为第i段系统侧h次谐波电压源的虚部。
同理,将用户侧等效为戴维南等值电路,如图3 所示。
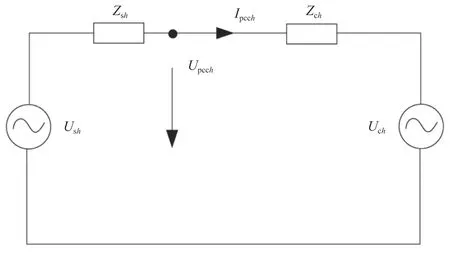
图3 系统戴维南等值电路
用户侧谐波阻抗平均值如公式(9)所示。
式中:Zchxi为第i段用户侧h次谐波阻抗的实部;Zchyi为第i段用户侧h次谐波阻抗的虚部。
用户侧谐波电压平均值如公式(10)所示。
式中:Uchxi为第i段用户侧h次谐波电压源的实部;Uchyi为第i段用户侧h次谐波电压源的虚部。
将公式(7)~公式(10)的值代入公式(1)、公式(2),然后比较Idh和Iuh的大小,就可以判别谐波源的位置。
3 试验分析
该文利用电力系统模块集进行仿真试验。假设在系统中存在1 个随机扰动的谐波源,建立试验仿真所需要的电路模型(如图4 所示),由测量可以得到公共耦合点的谐波电压和公共耦合点的电流,然后利用改进型偏最小二乘回归对测量出的谐波电压和电流进行分析,最终得到与原有设置值相近的估算值。
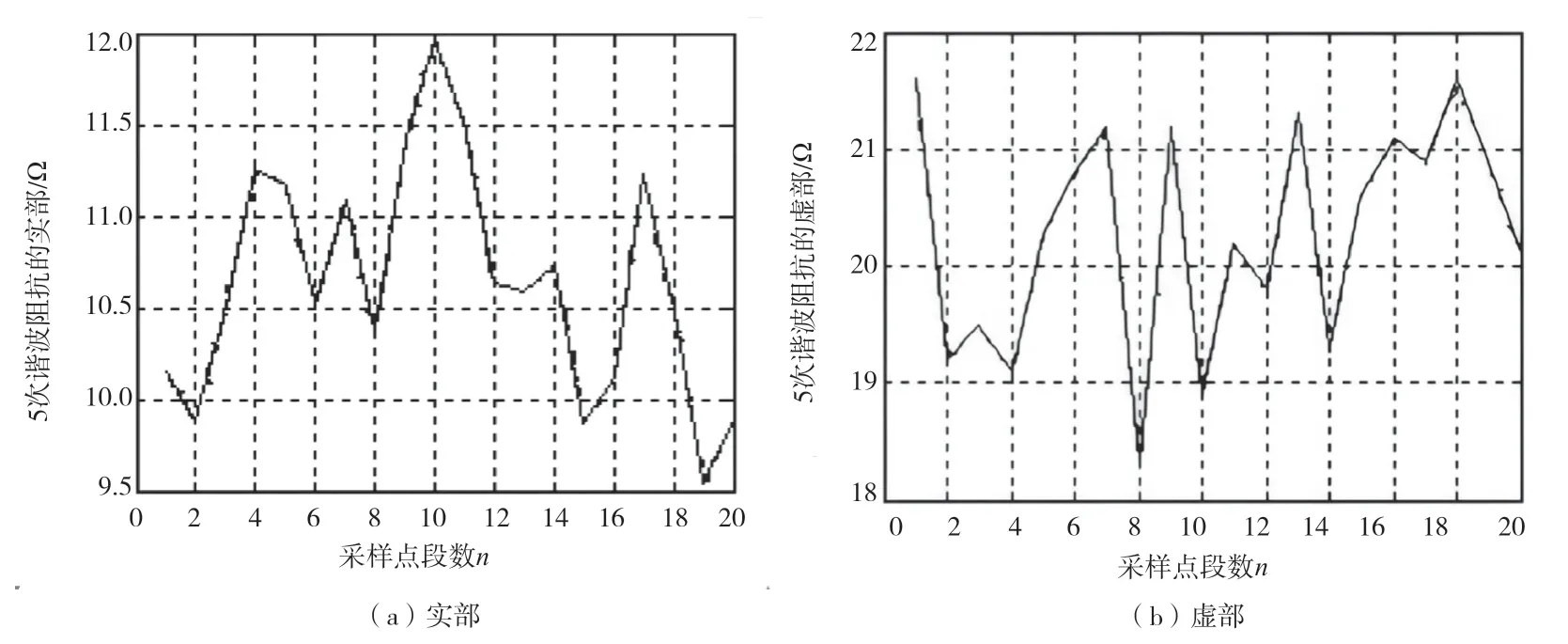
图4 系统侧的5 次谐波阻抗的实部和虚部
假设整个系统仅有5 次谐波,调整系统侧的谐波电压幅值,同时也调整用户侧的谐波源幅值,但是不能改变阻抗参数。系统侧对应的等值5 次谐波电压源Us为(5053°) V,用户侧对应的等值5 次谐波电压源Uc的平均值为(90+j780) V,系统侧对应的5 次谐波阻抗Zs平均值为(10+j20) Ω,用户侧对应的5 次谐波阻抗Zs的平均值为(50+j60) Ω。
在仿真的过程中,依次提取公共耦合点的5 次谐波电压和谐波电流,采样点数n为1 000 个(单位时间),总共分为20 段,每段有50 个点,然后对每段进行处理,即由改进型偏最小二乘回归法得到电源系统侧以及负荷用户侧的谐波阻抗,同时还需要计算谐波电压源对应的实部和虚部,将计算出的每段谐波阻抗的平均值作为该段的谐波阻抗,也可以看作是谐波电压源的实部和虚部(结果如图4~ 图 7 所示)。
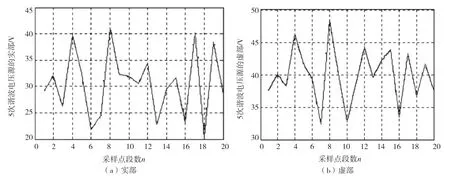
图5 系统侧的5 次谐波电压源的实部和虚部
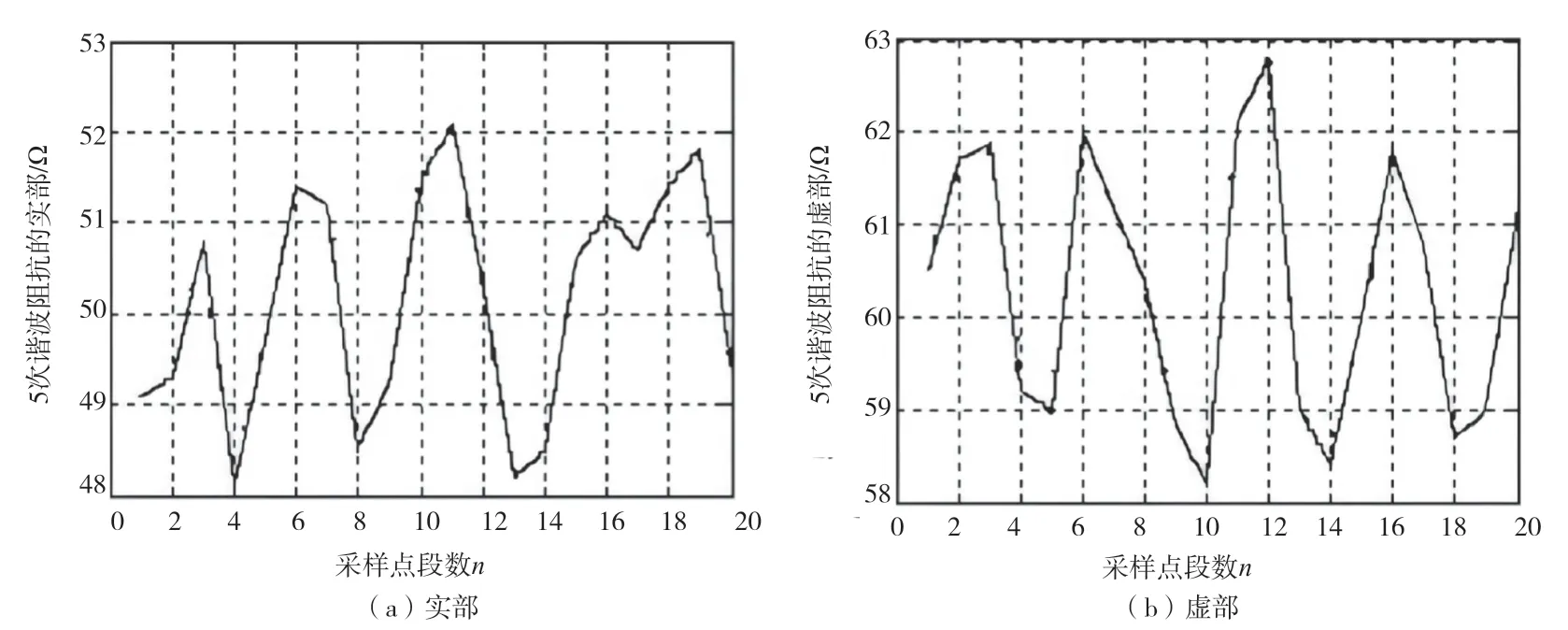
图6 用户侧的5 次谐波阻抗的实部和虚部
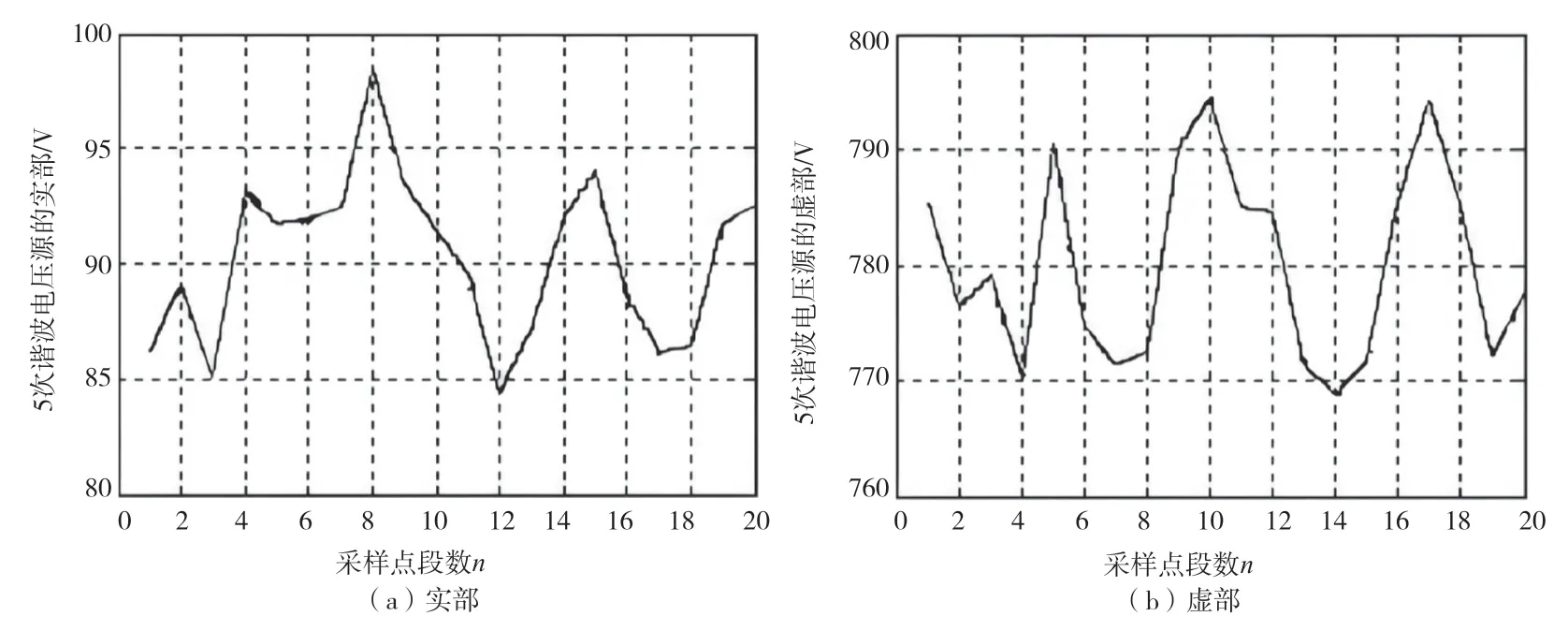
图7 用户侧的5 次谐波电压源的实部和虚部
运用改进型偏最小二乘回归法可以得到系统侧存在的5 次谐波阻抗Zs5的平均值,如公式(11)所示。
侧存在的谐波电压源Uc5的平均值,如公式(12)所示。
采用进型偏最小二乘回归法可以得到用户侧存在的5次谐波阻抗Zc5的平均值,如公式(13)所示。
由各个段估计获得的5 次谐波阻抗就可以得到用户侧谐波电压源Uc5的平均值,如公式(14)所示。
用户侧5 次谐波电流Ic5的平均值如公式(15)所示。
式中:Upcc5和Ipcc5分别为公共耦合点的5 次谐波电压以及5 次谐波电流。
将计算所得的数据代入公式(1)、公式(2)就可以得到从负荷侧流出的5 次谐波电流、从供电端流出的5 次谐波电流,分别如公式(16)、公式(17)所示。
因为|Iu5|>|Id5|,所以用户侧为主要谐波源。采用改进型偏最小二乘回归法进行仿真试验,主要针对系统的3 次谐波以及系统中其他各次谐波进行仿真计算,具体结果见表1。
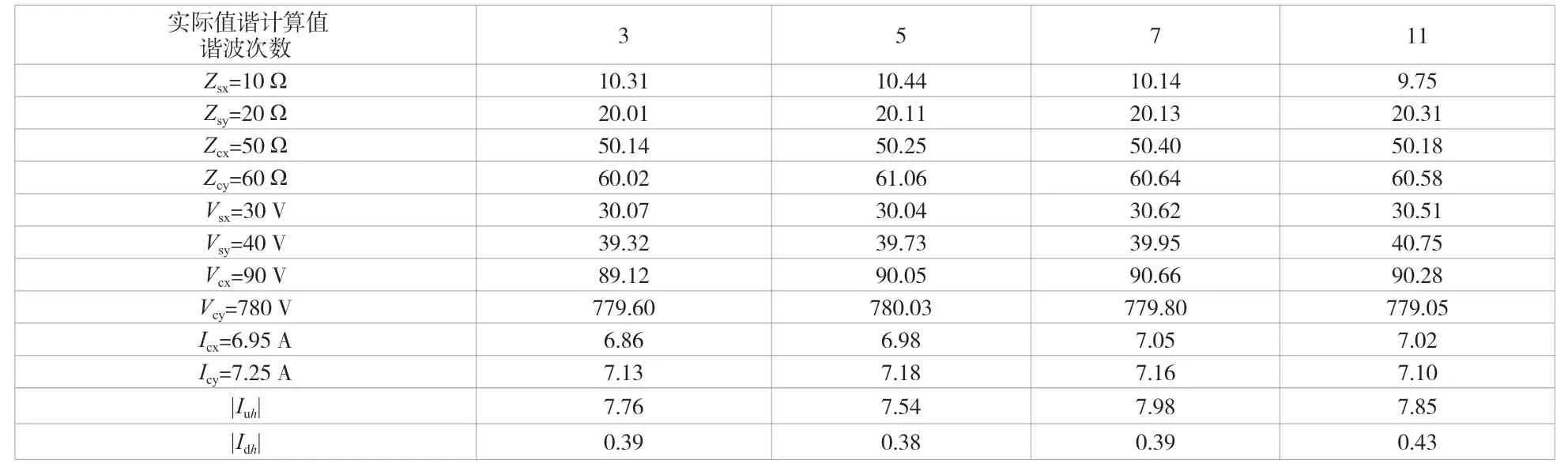
表1 各次谐波仿真计算表
由仿真结果可知,在谐波次数不同的情况下,当实际准确值与采用改进型偏最小二乘回归法计算得出的估计值较相近且|Iuh|>>|Idh|时,用户侧为主要的谐波源,该结果与最初设想的结果相同。
4 结语
该文将改进型偏最小二乘法应用于系统谐波源识别,利用正交投影法消除解释矩阵中与响应没有统计学意义的信息,解决了偏最小二乘法会遗漏与响应有关成分的问题,提高了估算精度。首先,利用改进型偏最小二乘法与阻抗法识别主要谐波源,最初采用改进型的偏最小二乘法进行回归计算,通过计算得出系统的谐波阻抗估计值。其次,与阻抗法相结合,得出谐波电流流出的大小,流出较多的一侧为主要的谐波源。最后,将通过试验仿真得到的数值与原有的设定值进行比较,从而验证了该文提出的方法能够快速、高效地识别谐波源。
