从学习视角对“教—学—评”一致性的理解与实践

陈永畅

《义务教育数学课程标准（2022 年版）》（以下简称“新课标”）强调要实现“教—学—评”一致性。华东师范大学崔允漷教授解读了“‘教—学—评三位一体”的理念，即在整个教学实践中，教师的教、学生的学以及对学习结果的评价之间的协调配合。围绕学习目标、学习活动和评价证据三要素，检验与判断学生要学会什么、怎样让学生学会、何以知道学会。那么单纯用原来教或学的视角都已不合适新时代学生的学习需求，必须找到教与学的平衡点和结合点，从学习视角来制定学习目标、开发学习活动、实施学习评价。在教的层面，要开发具有深度、能促进学生思维发展的学习活动，也要搭建起教材与学生的沟通桥梁，实现可持续发展；在学的层面，要突出学生的自主性、探究性和发展性，在教师的引领下领悟、迁移和归纳总结；在评的层面，要实现全面育人目标，满足学生多元化发展，因此要在练习上花心思、下功夫，实现链接、迁移和习得。

一、是什么：如何理解“教—学—评”一致性的内容要求

“教—学—评”一致性强调的是教学、学习、评价基于目标的协调一致，是将教师的教、学生的学以及对学习效果的评价有机融合，协同促进学生的学科核心素养发展。由此可见，确立清晰的学习目标是前提，设计促进思维发展的学习活动是媒介，制定科学合理的评价标准是保障。以新课标要求为纲领，将教材内容转化为学生的学习活动与任务，并设计辅以理解和升华认知的习题来检验学习效果，形成分阶的评价指标，再回头看是否达成了初期设定的目标。

例如，“倍的认识”一课中，教师可以根据教材和学情分析，从两个量的比较出发，引导学生理解“倍”的本质就是一个数中包含有几个另一个数作为目标。从教的视角考虑，简化了教材的情境图，动态化呈现教材的内容（如图1），把多余的数量关系去掉，只留下猴子和鸭子的数量，让学生从比较的本质入手；从学的视角考虑，探究活动中有两个已知量的比较，也有变化量的比较，甚至还有通过估测量的比较，从而让学生深度理解“倍”的变与不变；从评的视角考虑，我们的习题设计中，一阶是两个已知量的比较，二阶是变化量的比较，三阶则是估测量的比较，那么一阶是保底的，仅为原有认知的迁移，后面两个则是学生学习能力迁移和问题解决能力形成的很好的体现。那么，“教—学—评”一致性的实践本义应该是教中有学，学后有评，评中体现分层目标达成的一致性。因此教与学是辩证统一体，评则是两者效果实现的检验标准。

二、为什么：如何理解“教—学—评”一致性的实践价值

科学、合理实施“教—学—评”一致性，能够激发学生的学习动机，促进学生主体作用的发挥，提升学生的自主探究能力，真正让教学实现从“教师的教”到“学生的学”的转变，进而全面提升课堂教学的有效性和学生的核心素养。同时，其对小学數学课堂改革具有指导意义，也提供了一个新的研究视角。

（一）促进教学具有整体性

以前，有很多教师以课时目标来观照教学内容，有经验的教师可能也会以单元目标来观照教学内容，这样的教学设计思路还是有局限性的，也是造成学生知识储备零散、呈现点状的重要原因之一。新课标提出了要帮助学生搭建结构化思维，这需要通过结构化教学来达成，因此在教材解读和教学设计上须具有整体性观念。如“倍的认识”一课，在教学设计中教师从学生已有的两个量的“差比”经验入手，再到两个量的“倍比”过渡，然后再链接到“倍比”可以回归到乘法的意义，即“几个几”的本质来建构，不断地帮助学生建立一个知识网络，把一个个点连续起来，形成一个整体。教学中为什么我们要从乘法的视角来打开“倍的认识”呢？因为教材中还有一个目标就是让学生学会用除法来解决此类问题，而除法是乘法的逆运算，这样我们同样就能借助乘法帮助学生理解除法，同时学生建立了运算一致性的观念，也是教学整体性的体现。

（二）促进学习具有交互性

“教”的课堂不是时代主流，新课标明确指出要突出学生主体地位，即让学生参与学习过程，激活学生的思维，在交流分享、质疑思辨和探究归纳中形成认知。这需要在学习过程中体现交互性，只有相互对话和启发，才能真正产生智慧，提升学生的思维品质和核心素养。在设计“倍的认识”一课的学习活动时，师生通过梳理3 只猴子和6 只鸭子的倍数关系后，再引入12 只小鸟，那么小鸟的数量与鸭子是什么关系，与猴子又是什么关系呢？在比较红花和黄花的数量关系时，并不是给出整倍数的数量，而是要通过增加或减少其中的一个数量才能具有整倍数。把这些活动都设计“活”了，不再是知识的平行迁移，而是让思考“拐个弯”，才能增强交互性，才能真正让学生学会了，更会学了。在活动中，不仅是知识的习得，更有方法的掌握和思想的迁移，这就是基于“教—学—评”一致性设计的成果。

（三）促进评价具有进阶性

在当前的教学中，以“教”的视角思考已是一种惯性，因此教师可能会忽略评价的导学、导教功能。但实际上教学目标不再是培养只会做题的机器，而是要培养会思考、能解决问题的独立思想者。如何给予不同个体以不同的学习体验和思维进阶呢？通过习题分层设计来促进评价的个性化、多元化和进阶化已是势在必行。那么，我们在练习设计上就要对标分层评价，力求让每个学生都能在这一学习过程中收获知识和提升能力。在“倍的认识”教学中，笔者采用了基础练习对标知识迁移，检验学习效果，这是横向发展的；拓展练习对标能力迁移和思维发展，那么学生就要想办法增加数量、减少数量，或通过观测预估两个量的倍比关系，这是纵向发展的。一横一纵的评价倒逼我们的教学设计和学习设计都要指向学生的能力培养，因此就形成了三者的一致性。

二、怎么做：如何理解“教—学—评”一致性的实践运用

解决“教—学—评”一致性存在的问题，办法在于提高教、学、评的相关性，研究教什么、学什么、评什么的问题。新课标不仅明确了“为什么教”“教什么”“教到什么程度”，而且强化了“怎么教”的具体指导，如何落实“教—学—评”一致性的实践运用呢？下面笔者以“倍的认识”一课为例谈谈理解。

（一）聚焦知识结构，设计“教—学—评”的碰撞点

课的开篇，教师先出示4 只鸭子和3 只猴子让学生比较，学生会说鸭子比猴子多1 只，教师追问：那再增加1 只鸭子呢？这时，学生又会说鸭子比猴子多两只。这一过程就是为了激活学生的已有知识经验，把“比较”这把尺子调出来。当教师出示6 只鸭子和3 只猴子时，抛出的问题是：多出来的鸭子和猴子的数量是什么关系呢？然后，引导学生通过圈画，把3 只猴子当成1 份圈起来，那鸭子的数量就是这样的2 份，从而引出了“倍”。这就是帮助学生建立整体观念，梳理出知识结构：原来“倍比”是“差比”的进化，“倍”就是指一个数中包含了几个另一个数，那么1 份数对于“倍”的产生就特别关键。这里教师的教是为了学生的学铺垫的，学生有了这一次深度对话，真正地明白了倍的本质，并且能从“几个几”的概念上去理解，这样的教就会让学生在学时能有整体观照知识的习惯，教与学也就真正形成了统一体。

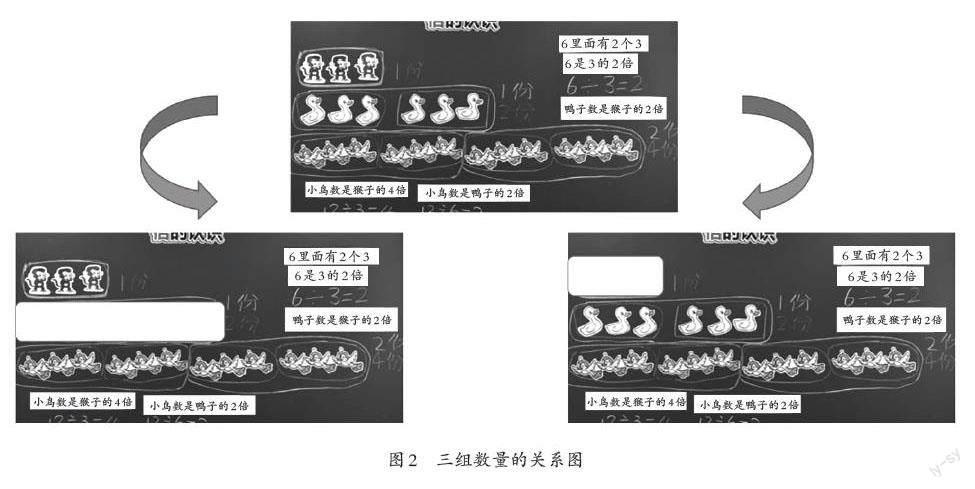
为什么这样说呢？在第二环节中，教师放手让学生去探究：如果现在又来了12 只小鸟，那么小鸟的只数是猴子的几倍，又是鸭子的几倍呢？同样是12 只小鸟，为什么它一会是猴子的4 倍，一会又是鸭子的2 倍呢？能通过圈一圈、比一比来解释你们的结论吗？（如图2）这里学的矛盾点在于1 份数的不同，因此倍数也就不同了。这是建立在第一环节教的基础上思考的，在第二环节多出一个干扰的比较量。教师引导学生再次理解：倍要聚焦两量比较，而且比的“标准”很重要。此外，这也为发展性的“评”奠定基础，学生学的不是死板的知识，而是灵动的、能促进思考的知识。如此一来，学生的知识形成是具有链接的，是网络状的，更是结构化的。教的时候，教师若只是打开一个碰撞点，在学的时候则需要以它为起点，不断地往深处挖掘，陆续扩大横截面，渐渐地往纵深发展。其实，有了这样的思维结构后，学生再学习“用分数表示两个量的数量关系”便水到渠成，因为分数就是对倍的拓展，它们的本质是一致的。可见，通过知识结构或思维落差这样的碰撞点，畅通学生的学习过程，丰富评价内容和标准，是培养具有思考能力的时代新人这一目标的重要一环。

利用结构化撬动“教—学—评”一致性，能找到教与学的契合点，体现学生主体地位，并汇聚成教学的有机融合体；能找到从教到学，再到评的一条主线，而且是逐步递进的主线，这样便能保持三者的一致。

（二）凸显主动探究，设计“教—学—评”的生长点学生是学习的真正主体，那么如何设计基于“教—学—评”一致性的探究任务，又如何深化学生对“倍”的理解呢？答案就是挖掘出知识的生长点、能力生长点和思维生长点。在教学中，我们设计了两个探究任务。

任务一：

1. 增加多少朵红花（图3 中上面一行），红花是黄花（图3 中下面一行）的2 倍？

2. 减少多少朵黄花（图3 中下面一行），红花（图3 中上面一行）是黄花的2 倍？这个任务将黄花当成1 份数，增加红花的数量，或者把红花当成2 份数，减少黄花的数量。这个设计通过一增一减，在不断地变化1 份数中理解“倍”的内涵，把“倍就是指一个数中包含有几个另一个数”这个本质也就再次巩固了。另外，也搭建了乘法和除法的沟通桥梁，打破了固定的关系比较，这就是生长点的体现，让学生打开分析问题、思考问题的视角，从而真正地从“教—学—评”一致性切入。

任务二：图形王国里，圆形哥哥说它的个数是三角形弟弟个数的3 倍，你能用你的智慧帮帮它们吗？请你画一画。

学生画出很多种不同的答案，有的画出了3 个圆形和1 个三角形，有的画出了6 个圆形和2 个三角形，有的画出了9 个圆形和3 个三角形……这时，教师再抛出一个问题：为什么会有这么多不同的画法呢？你们有什么想说的吗？让学生再次发现3 份数会随着1 份数的变化而变化，倍数是会被比較的“标准量”影响的。这样的探究活动设计就能在知识生长、思维生长和能力生长上给予学生强有力的支持。

不难看出，以上的教与学不再只是停留在单一知识层面，而是上升到学科素养层面，习题的设计也不再仅考查知识，而是有能力拓展，更有思维方式的培养，这就是具有“教—学—评”一致性、三者间相互呼应的高质量课堂教学。

（三）关注思维品质，设计“教—学—评”的延展点无论是教学过程还是学习过程，教师始终要关注延展性，即让学生能将习得的知识与技能迁移到问题解决中，会选择不同的解决问题的方式，会用融会贯通的思维去审视问题。那么，教师就需要抓住“教—学—评”一致性的关键，设计具有延展性的问题、活动或辨析。在前面几个环节里，在比较两个量的倍数关系时，学生都是可以通过观察直接判断或得出结论的，这不禁让笔者反思：对标新课标要求，这样已经足够了吗？答案显然是不够的，教师需要提供更多具有思维品质的问题、活动，让学生产生质疑、分歧，在辨析中深刻理解知识的内涵，更重要的是发展素养。为此，在课的最后，教师又设计了这样的一个环节：猜一猜下面的两个长方形存在什么倍数关系，两条线段间又存在什么倍数关系。（如图4）

看似很平常的一个活动设计，需要学生调动自己的原有经验，通过目测去给长方形和线段增加辅助线，然后再比较。这一过程不再是单纯地考查两个量的数量关系，学生的估测、量感和问题解决的能力都在这里有了新的生长点。这样的延展是基于学生素养发展全局来考虑的，这样的活动设计才不是为了学习而学习，而是真正地将素材的作用无限放大，激活学生思维，提高分析问题、解决问题的能力。这就是用评的方向来决定教与学，促进教与学的改革。此外，教与学需要更加开放，要聚焦问题开展讨论，呈现学生的生成，点燃学生的思辨。这样的课堂就体现了新课标要求的“教—学—评”一致性。

由此，在教育实践中高质量地实现“教—学—评”一致性，需要教师沟通教、学、评三者间的联系，在课前做足工作，基于新课标、学生学情以及知识结构体系，把握学科的知识本质，确立适切的学习目标，并围绕学习目标设计相应的探究活动。此外，需要教师研制评价检验的习题，让“教—学—评”融为一体，从而提升教学质量，优化学习模式，提升学生素养。

（责任编辑：杨强）