基于PSO-RF的冲击地压危险性等级预测研究

刘佳琪,杨超宇

(安徽理工大学 经济与管理学院,安徽 淮南 232000)

冲击地压(也称岩爆)是指在煤矿开采过程中,煤矿和岩体在一定条件下释放变性势能,而产生的突然猛烈释放,并伴随岩体突然爆裂、垮落或抛出等现象。通常具有很强的危害性、突发性、复杂性、诱发性等特点,是煤矿的主要自然灾害之一[1]。近年来陆续发生的山东龙郓、吉林龙家堡、河北唐山、山东龙堌、陕西胡家河等数起严重冲击地压事故灾害,造成了严重的人员伤亡和重大的经济损失,甚至威胁到我国能源的安全[2]。如何准确有效预测冲击地压危险性等级,已成为煤矿井下开采急不可待的问题。

目前传统的对冲击地压预测方法概括起来主要有:经验类比法、现场检测法、综合预测法等。上述方法虽然在实际运用中取得了一定的效果,但是都有一定的局限性。经验类比法主要是用来定量分析,但没有定性的理论公式支撑,反映出主观性较强,过于依赖经验等缺陷。现场检测法主要是依据前向传过来数据的变化规律从而判断冲击地压的危险性,代表方法有:微重力、微震法、电磁辐射法等[3]。该类方法的数据往往存在失真、缺失的现象。综合预测法主要是基于冲击地压样本数据和特征因子的距离判别模型、模糊均值评价等一些涉及多元统计分析的方法,另外还有粒子群(Particle Swarm Optimization,PSO)优化BP神经网络(PSO-BP)模型、广义神经网络(Generalized Neural Network,GRNN)模型、概率神经网络(Probabilistic Neural Network,PNN)模型等[4-9]。这些新理论与方法有其自身的优势,同时也存在一定的局限性。由于因子间受多种因素耦合影响、关键特征的描述不充分,这很大程度上影响着评价方法的客观性;再者,BP、GRNN神经网络模型客观上存在收敛速度慢、易陷入局部最优、需要对大量参数进行调试等缺点,对于冲击地压预测的小样本、非线性问题,这些模型的预测准确度并不高。

鉴于上述的理论研究,本文构建了一种能够真实刻画出输入变量与输出变量间关系、预测准确率高并具有极强的非线性逼近能力的粒子群优化随机森林(Random Forest,RF)组合模型。利用PSO优化RF建立新的冲击地压危险性等级预测模型,将与未经处理的RF模型、决策树(DT)和梯度提升分类模型(Gradient Boosting Classifer,GBC)、自适应提升算法模型(Adaptive Boosting,AdaBoost)等其他基于树的模型进行对比分析,选取准确率作为评价指标,并将各模型的准确率使用混淆矩阵可视化,验证PSO-RF模型在冲击地压危险性等级预测的优越性。

1 基于PSO的改进RF预测模型

1.1 RF预测模型

RF算法是由Breiman等于2001年提出的一种以随机方式建立的,包含多个决策树的非线性和非参数分类器[10]。通过自助重复采样技术(bootstrap)随机有放回地对样本进行抽样,抽取到的样本作为训练集,未抽取到的作为验证集,随机对样本特征进行抽样,利用基尼不纯度最小和信息增益最大的原则从这些信息集合中选择一个最优的信息来划分决策树,然后,重复上述步骤形成随机森林,分类结果取决于决策树的投票众数。RF模型的核心思想是决策树算法的改进,单个决策树的分类效果未必好,但由于依靠多棵树并行的训练方式,所以每颗子决策树能够保留部分样本及特征,这使得它具有很强的容噪声能力,数据集不会出现过拟合现象。

但是,因其自身结构的特殊性,这使得比其他类似树模型需要更多的训练时间,并且RF模型中的决策树数目、决策树最大深度及其他超参数的选取会对RF模型的预测造成很大影响。

1.2 PSO-RF预测模型构建

PSO算法是通过设计一种无质量的粒子来模拟鸟群中的鸟[11]。首先,在d维空间内随机初始化粒子的速度大小Vi∈(Vmin,Vmax)和位置大小Xi∈(Xmin,Xmax)两个属性,将RF模型中特征属性子集作为粒子群自己属性;其次,将RF模型的十折交叉验证的平均值作为PSO的适应度函数,并计算各个粒子的适应度值F_t、个体极值P_best以及全局最优解G_best;最后,迭代更新粒子的速度和位置,当RF模型十折交叉验证均值最小即适应度函数值最小时,可以得到模型在寻优条件下的最优参数。更新公式,如式(1)和式(2)所示。

(1)

(2)

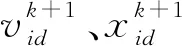
随机森林模型预测的精度和速度主要受子决策树的个数n(n_estimators)和决策树最大深度m(max_dapth)的影响,决策树n选取太小容易出现欠拟合,太大不能显著提升模型,最大深度m的选取好坏又会影响模型的训练速度。利用初始化后的粒子群模型对随机森林模型中的决策树的个数和决策树最大深度进行寻优,一方面,在提升模型的预测精度下,还能提高模型的泛化能力;另一方面,将决策树个数和决策树最大深度2个优化参数作为各个粒子的维度,即粒子只需在二维空间内搜索最优值,能够有效地减少粒子群寻优的时间,可以在保证模型预测能力的基础上,还能提升模型的预测时间。模型的预测流程,如图1所示。

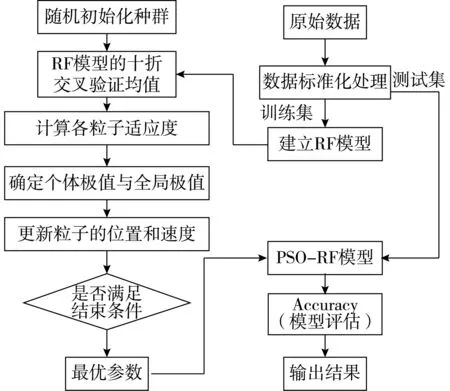
图1 PSO-RF模型的预测流程

2 数据预处理及特征分析

2.1 确定样本评价指标与等级

冲击地压特征的选取需遵循一定的可行性和适用性。特征选取过多,会造成信息重叠,影响模型效率,特征过少无法表现出预测的完整性和全面性。本文依据强度、能量、冲击倾向性准则,选取最大切应力(σθ)、单轴抗压强度(σc)、单轴抗拉强度(σt)、应力系数(σθ/σc)、脆性系数(σc/σt)、弹性能指数(Wet)6个物理力学特征作为冲击地压危险性等级预测评价指标。另外,按照应力状态和冲击显现强度的不同,本文将冲击地压的强度分为四个等级,即:第一类无冲击(None)、第二类轻微冲击(Light)、第三类中等冲击(Moderate)、第四类强烈冲击(Strong)。各冲击地压等级分级标准[12]如表1所示。

表1 冲击地压等级分级标准

2.2 获取样本数据

本研究在国内外研究冲击地压[13-15]的基础上,搜集了344条完整的冲击地压工程数据,部分数据如表2所示。在该样本数据集中,四类冲击地压分别占比情况为:无冲击14.5%、弱冲击35.8%、中等冲击28.5%、强烈冲击21.2%。

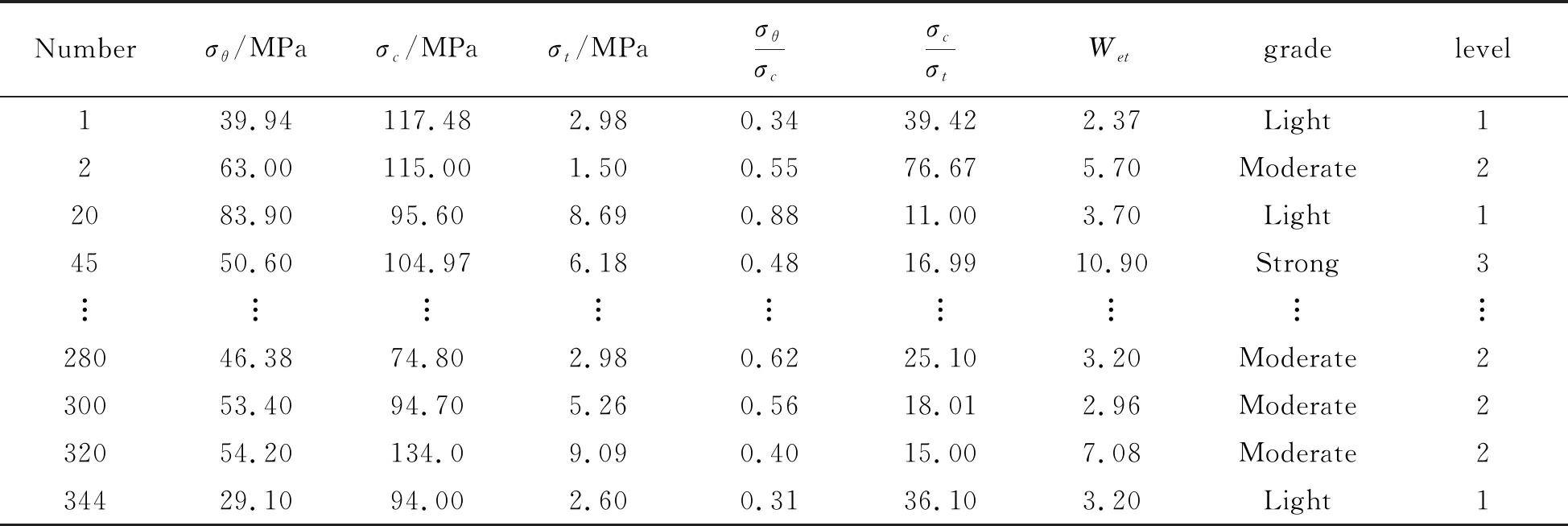
表2 冲击地压部分数据

考虑到表1中原始数据的量纲不同,使得数据差异较大,需对数据进行标准化处理。标准化公式如式(3)所示,标准化后的数据如表3所示。

表3 标准化后的数据

(3)

其中,xi和xi*分别为各指标第i个样本的值和标准化后的值,μ为该指标下样本的均值,σ为该指标下样本的标准差。

2.3 特征变量分析

为了分析各影响特征在不同等级下的分布情况,本文分别绘制了各个影响特征的核密度分布,如图2所示。

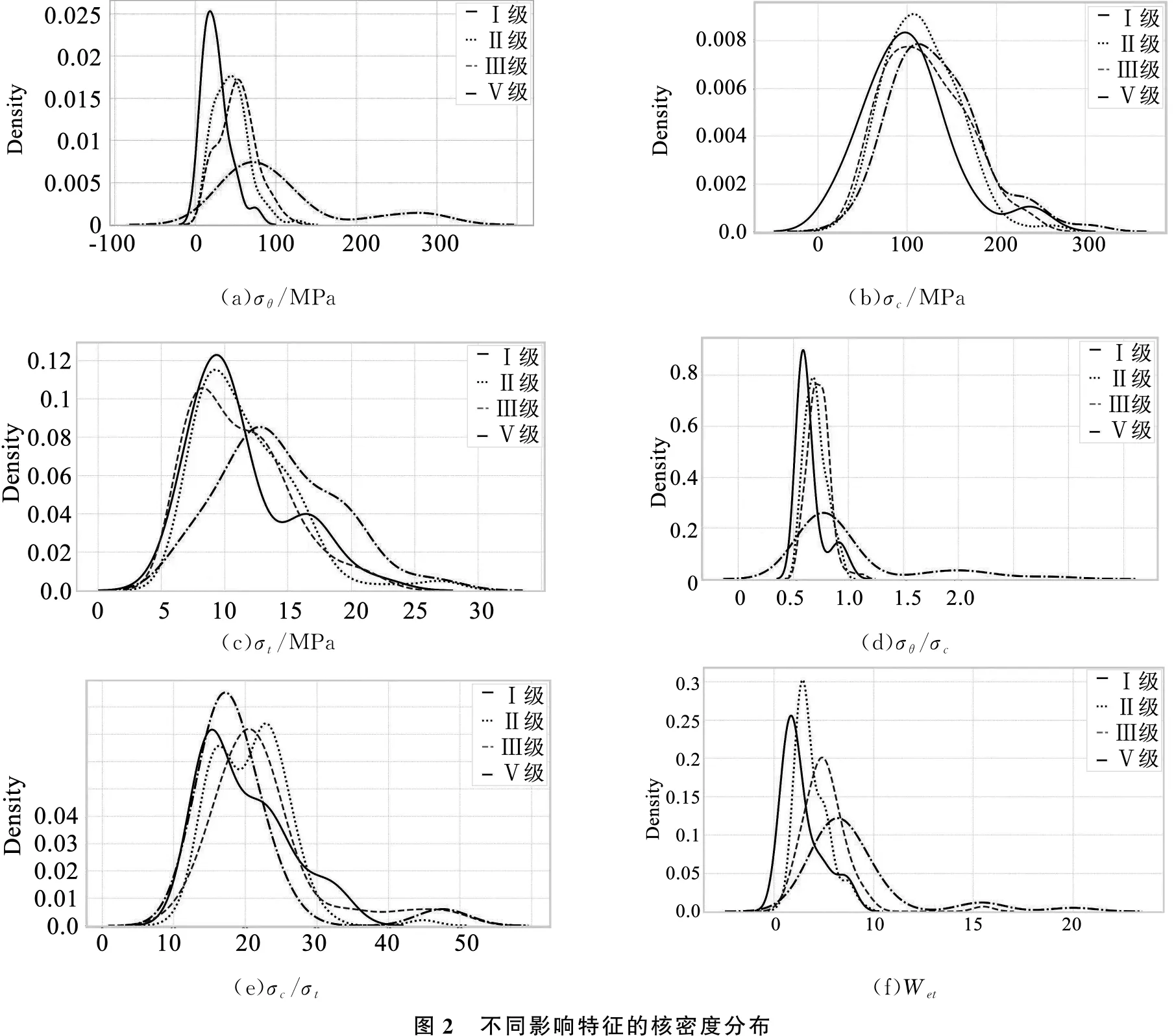
由图2(a)、图2(b)、图2(d)、图2(f)可知,其分布情况较类似,在不同冲击地压等级下呈正相关,冲击地压等级越强,最大切应力、应力系数越大。其中图2(a)对于无冲击、较弱冲击呈正态分布,对于中等冲击、强冲击分布较分散,图2(b)在不同等级都呈正态分布,图2(d)较弱冲击、中等冲击呈正态分布,在无冲击、强冲击中分布较分散,图2(f)无冲击、中等冲击呈正态分布,较弱冲击、强冲击分布较分散。图2中的(c)、(e)的分布情况较类似,与冲击地压等级的相关性不大,等级越高,对应的数值并非越大,其中图2(c)对于无冲击、较弱冲击、强冲击呈正态分布,对于中等冲击的分布较分散,图2(e)对于中等冲击和强冲击呈正态分布,在无冲击和较弱冲击中分布较分散。总的来看,虽然在不同的特征下,各个等级间的分布情况是有所差异的,具有一定的区分度,但是,有不少等级包含较多的离群值甚至出现范围相同的情况,而离群值的多少将直接影响预测的精度。因此,本文选用能够考虑各影响特征因素并且具有较高预测精度的基于树模型的随机森林模型进行预测。

3 实验及结果分析

3.1 模型训练

首先,将数据标准化后,按照8:2的比例将原始数据划分成训练集和测试集,并且训练集和测试数据中各类数据的比例和原数据集保持一样,减少因数据间不平衡而导致模型预测精度的误差。然后,将训练集数据进行初始RF模型训练,取十折交叉验证的平均准确率作为粒子群的适应度函数。最后,利用PSO对适应度函数进行迭代寻优,当准确率出现最高时,取出该模型的最优参数决策树个数n和最大深度m。具体结果如图3所示,当迭代次数在60次以后,适应度函数值趋近于稳定,此时搜索到的RF最优参数为n=22,m=45。

图3 PSO-RF参数优化

3.2 模型预测与对比分析

将测试集数据带入优化好的PSO-RF模型,验证模型的预测精度,同时为了更好地验证PSO-RF模型在预测冲击地压危险等级的优势性,本文将与未经处理的RF模型、DT模型、GBC模型、AdaBoost模型以及lightBGM等其他基于树模型的预测结果进行对比分析。另外,为了有效评估各模型预测冲击地压等级的效果,本文以准确率(accuracy)作为评价指标,并利用可以比较真实表达分类精度的混淆矩阵(confusion matrix)对预测结果进行可视化展示。各模型的准确率和混淆矩阵预测结果,如表4所示。

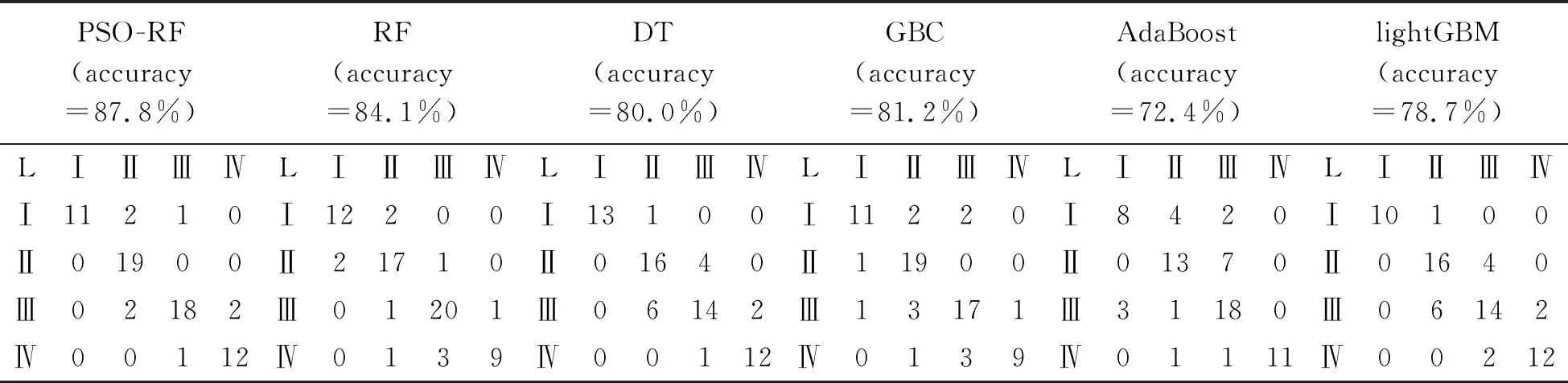
表4 各模型的准确率和混淆矩阵预测结果

通过表4中的实验结果对比可见,主对角线为预测正确的样本数,其他为预测错误的样本数,各模型的预测准确度从高到底依次为PSO-RF模型、RF模型、GBC模型、DT模型、lightGBM、Adaboost模型。相比于其他5种树模型,本文PSO-RF的预测准确度为87.8%,基于PSO-RF的冲击地压等级预测模型具有较好的预测效果。

4 结论

(1)利用核密度分布图对影响冲击地压危险性等级的特征进行分析,发现冲击地压等级与弹性能指数、最大切应力、单轴抗压强度等呈正相关,与脆性系数呈负相关。

(2)利用PSO算法对RF模型的最大深度m和子节点数n进行寻优,将得到的最优参数带入PSO-RF模型进行测试,并与未经优化的RF模型、GBC、Adaboost等其他基于树的模型进行对比分析,将准确率作为评价指标,利用混淆矩阵可视化各模型的预测结果,结果显示,PSO-RF模型、RF模型、GBC模型、DT模型、lightGBM、Adaboost的准确率分别为:87.8%、84.1%、81.2%、80.0%、78.7%、724%,PSO-RF模型的预测精度最高。