高保真中子输运程序HNET共振计算方法研究
2023-06-03朱雁凌郝琛张乐瑞
朱雁凌,郝琛,张乐瑞
(1.哈尔滨工程大学 核安全与仿真技术重点学科实验室,黑龙江 哈尔滨 150001;2.清华大学 核能与新能源技术研究院,北京 100084)
近年来,精细化中子物理计算是核领域兴起的一个技术研究热点。哈尔滨工程大学核科学与技术学院开发了全堆芯一步法高保真中子输运计算程序(High fidelity NEutron transport program for 3-D nuclear reactor whole core,HNET)。HNET基于多级加速理论,在三维并行、多级CMFD计算框架下,采用堆芯一维轴向先进节块计算方法或离散纵标法耦合堆芯二维径向特征线法的2-D/1-D方法开展全堆芯三维精细化中子输运计算。其中,共振计算得到的有效共振截面直接影响中子输运计算的精度,是HNET程序的重要计算模块。最初HNET版本中采用HELIOS程序的47群多群微观核截面数据库进行共振计算。应用更普适的核数据库,增加HNET计算程序的适用性,需要拓展新的数据库。但前提需要对于共振计算方法进行优化,确保基于新的数据库,可高效、精确地开展共振计算。
传统的共振计算方法主要包括等价理论方法、超细群方法和子群方法等。超细群法[1]将共振能区划分为上万群,可以准确地描述共振能群截面随能量的变化,但是计算效率较低。等价理论方法[2]具有较高的精度和效率,但是难以处理复杂几何问题。子群方法[3-4]具有较高的精度以及良好的几何适应性,在国际上被广泛应用,如HELIOS[5]、DeCART[6]、nTRACER[7]等程序,因此HNET采用子群方法开展共振计算。但是,传统子群方法在计算子群参数时,容易出现子群参数为负值的问题,并且没有考虑多共振核素之间的干涉效应,因此需要进一步处理和优化。Peng等[8]采用最优化拟合法生成子群参数;Joo等[4]采用本底迭代法计算有效共振截面;Bacha等[9]结合子群方法与共振干涉因子法与来处理局部共振干涉效应。此外,传统子群方法在开展共振计算时,存在频繁调用中子输运求解器以求解子群固定源方程的现象[10],会严重影响计算效率。
HDF5文件格式能够以灵活、高效的I/O功能支持各种海量、复杂的数据,具有读写速度快、便于用户快速进行数据查找等优点[11]。本文基于自主开发的HDF5格式69群截面数据库,研究并优化了子群共振计算方法,实现了精细化中子物理计算程序HNET的高效、精确共振计算,为后续中子输运计算提供了精确的多群共振截面。针对子群参数的计算,本文采用帕德近似法计算子群参数,并通过调整拟合点对其优化,使计算获得的子群参数符合物理意义,以确保子群参数计算的准确性。为提高计算效率,本文采用等效单共振群方法,并对共振核素进行分组,只对每组的代表性核素进行固定源方程求解以提高计算效率。最终,基于上述方法,开发了HNET共振计算模块,对无限均匀问题、燃料栅元问题及VERA基准题进行计算,并将结果与蒙特卡罗程序统计结果比较分析,验证了优化后共振计算模块的准确性。
1 理论模型
1.1 子群参数计算
子群方法的基本思想是将共振能群从截面的角度进行离散,通过子群截面和子群概率来描述剧烈振动的核反应截面值。子群形式的能群有效共振截面可表示为:
(1)
式中:g表示能群;N表示子群数目;σx,n和pn分别为反应道x的第n个子群截面和子群概率;φn为第n个子群通量。由式(1)可知,有效共振截面只与子群参数和子群通量相关。子群计算方法的流程主要为:先计算子群参数,然后采用输运求解器求解子群固定源方程得到子群通量,最后用子群通量归并子群截面获得有效共振截面。
应用子群方法开展共振计算时,忽略裂变源项及上散射项,且不考虑共振散射截面,在中间近似条件下,子群固定源方程[4]可表示为:
Ω·∇φg,n(r,Ω)+(Σa,g,n(r)+λΣp,g)·
(2)
式中:λ为中间近似因子;Σa,g,n为子群宏观吸收截面;Σp,g为宏观势散射截面,λΣp,g=∑λiNiσp,g,i,Ni和σp,g,i分别为第i个核素的核子密度及其第g群的微观势散射截面。从式(2)可以看出,子群通量反映了几何结构及材料组成对有效共振截面的影响,且子群固定源方程与多群输运方程在形式上相同,与高保真中子输运方法相容性好。由于子群固定源方程的源项与通量无关,可同时对多个子群固定源方程独立求解,提高计算效率。
在制作与背景截面相关的共振截面表时,假设无限均匀介质中只存在一个共振核素R,并忽略非共振核素的吸收截面[12],则由式(2)可得中子标通量计算公式:
(3)
式中:σb为共振核素R的背景截面,其定义为σb=λΣp/NR。当只有共振核素存在时,背景截面达到最小值λRσp,R,通量“凹陷”的程度较深。当背景截面非常大时,通量大小接近于1,此时共振核素对通量的影响很小。将式(3)代入到式(1)中,可建立中间近似条件下有效共振截面与子群参数和背景截面的关系:
(4)

(5)
式中:cn与dn为与子群参数相关的多项式,且dN-1的值为1。结合文献[10],将数据库中2N-1组背景截面及对应的共振截面代入(5)求解拟合系数cn与dn,进而得到子群吸收截面σa,n与子群概率pn。其他反应道(总截面、裂变截面等)子群截面的计算表达式为:
(6)
式中:ei为多项式系数,可通过最小二乘法或切比雪夫拟合法对不同背景截面下的其他反应道截面进行拟合求得。
如果共振核素R某一能群截面的波动较小,而选取的子群数目又过多,会导致拟合多项式的阶数过高,出现子群截面为负的现象。为使子群参数符合物理含义,在计算得到拟合参数cn与dn后,将式(5)拟合多项式因式分解(以子群数目N=3为例):
(7)
若|x1-y1|≤ε或者|x2-y2|≤ε(x1 (8) 若|x1-y1|≤ε且|x2-y2|≤ε(x1 为验证子群参数的准确性,将子群参数代入到式(4),反推数据库中不同背景截面下的共振截面,并将其与数据库比较,计算偏差可表示为: (9) 为避免出现子群参数为负值的情况,并保证子群参数的准确性,在计算子群参数时,需要不断地调整拟合背景截面点,直到计算偏差δerror小于1%且子群参数均为正值。为增加帕德近似法中背景截面点的选取方案,HDF5格式多群截面数据库提供30个背景截面点。 传统的子群方法需要分别对各个共振核素所有共振能群的每个子群截面所对应的子群固定源方程进行求解。为减少求解子群固定源方程的次数,可采用等效单共振群方法进行优化[4]。由式(2)可知,子群固定源方程的源项只与散射源项有关,且中间近似因子λ和势散射截面σp随能量变化的幅度很小,因此在求解子群固定源方程时,可将所有共振能群等效为一个能群。此外,子群固定源方程与子群概率无关,而与各个子群截面的值有关。在同一区域,如果不同共振核素的子群截面相同,即使它们的子群概率不同,它们的子群通量也会相同。因此,可以事先挑选一组子群吸收截面σm,只对这组特定子群截面所对应的子群固定源方程进行求解。特定子群截面的个数和取值应尽可能地代表实际燃料子群截面的范围,本文选取的10个特定子群截面分别为:0.1、10、50、100、200、300、500、1 000、2 000和10 000 b。 当某一区域存在多个共振核素时,各共振核素间的共振峰可能相互重叠,形成共振干涉效应。本文结合HELIOS程序[5]采用Bondarenko迭代方法[9]对共振干涉进行修正。同时,为了进一步提高计算效率,对共振核素进行分组以加速Bondarenko迭代方法。如表1所示,基于共振核素共振峰之间是否重叠,将共振核素分为若干组,并在每组中挑出一个代表性核素。认为同一组的共振核素间存在共振干涉效应,不同组间的共振干涉效应忽略不计。 表1 共振核素组别及代表性核素Table 1 Resonance categories and representative isotopes 基于上述方法,在开展共振计算时,只需针对各组代表性核素特定的子群截面进行子群固定源方程求解,减少了求解子群固定源方程所需的时间。以235U和236U为例,当特定子群吸收截面的数目取为5时,子群固定源方程的计算次数为5,而传统子群方法需要的计算次数为130(2×13×5)。此时,式(2)中的Σa及λΣp可由无限稀释条件下共振能群吸收截面对应的共振积分Ig,∞加权得到: (10) (11) 式中:下标i表示归属于第k组的共振核素;下标r表示第k组的代表性共振核素;σm为特定的子群吸收截面。 由于共振截面表是在均匀系统下制作而成,而实际情况多为非均匀系统。因此在求得特定子群通量φm后,通过逃逸截面Σe将非均匀系统的背景截面与均匀系统等价: σbm=σb+Σe(σm)/NR (12) 逃逸截面Σe的定义为: (13) 在求出与σm相应的逃逸截面Σe后,实际子群截面对应的逃逸截面采用对数插值获得,然后通过式(12)计算背景截面,最后将背景截面代入到式(3)计算子群通量。结合Bondarenko迭代方法,共振核素i的有效共振吸收截面[4]可表示为: (14) 式中:σx,i表示其他共振核素j的吸收截面对当前共振核素i的影响: (15) 由于σx的大小取决于σa的值,而σa的值又与σx相关,因此需要通过迭代计算获得最终结果。 本文采用基于ENDF/B-VII.0加工得到的HDF5格式69群截面数据库,其共振能群为第15~27群,共振能量范围为9 118~4 eV。为验证共振计算结果的准确性,将蒙特卡洛程序的统计结果作为参考值。在蒙特卡洛程序中设置500代计算,每代投入50 000粒子,前50代为非活跃代数。在获得蒙特卡洛程序的统计结果后,采用通量体积权重的方法计算出能群平均截面的参考值。 为验证子群参数的准确性,如表2所示设置仅由单个共振核素(235U或238U)和1H所组成的无限均匀问题,不考虑实际几何结构、材料非均匀性等因素。通过调整核子密度比例来改变共振核素背景截面的大小,其中1H与235U核子密度的比例选为1 000、500、100;1H与238U核子密度的比例选为10、5、1。 表2 无限均匀问题核素组成Table 2 Compositions for infinite homogeneous cases 当温度为600 K时,无限均匀问题有效共振吸收截面的相对误差如图1所示。由图1(a)可知,235U除了第27群(9.88~4 eV)外,各吸收截面都具有较高的精度,最大相对误差不超过0.2%。从图1(b)可以看出,随着1H与238U核子密度比例的减小,238U背景截面逐渐减小,各能群有效截面的相对误差在不同程度上都有所增大,尤其是在case 1~6(此时238U背景截面在20 b左右)。其原因主要是在计算子群参数时,并没有选取很小的背景截面作为拟合点,导致当238U的背景截面较小时,子群参数对截面的拟合精度有所下降。 图1 无限均匀问题吸收截面的相对误差Fig.1 Relative error of absorption cross sections for infinite homogeneous cases 图2对比了温度为293、600、900和1 100 K时,235U(case 1-3)和238U(case 1-5)有效共振吸收截面的相对误差。由图2可知,在所选的温度范围内,235U和238U吸收截面的相对误差在温度上没有明显的趋势性变化,温度变化对子群参数计算精度的影响比较小。总体上,在不同背景截面和不同温度下,单共振核素无限均匀问题有效共振吸收截面的相对误差均小于1%,这表明子群参数的准确性高。 图2 不同温度下吸收截面的相对误差Fig.2 Relative errors of absorption cross sections at different temperatures 为验证共振计算模块处理共振干涉效应的能力,针对只含燃料和慢化剂的单栅元问题进行计算,其中燃料棒半径为0.409 6 cm,栅元半边长为0.63 cm。如表3所示,将燃料的组成设置为238U、235U和16O,并根据富集度设置不同的核子密度。慢化剂由1H和16O组成,它们的核子密度分别为0.022 116 3×1024、0.044 232 6×1024cm-3。燃料和慢化剂的温度均为600 K。 表3 不同富集度下燃料组成Table 3 Fuel composition at different enrichment 图3显示了不同富集度下,燃料棒内共振核素棒平均吸收截面的相对误差。棒平均吸收截面是指采用通量-体积加权方式归并得到的燃料棒活性区平均截面。 图3 燃料棒吸收截面的相对偏差Fig.3 Relative errors of absorption cross sections in fuel rod 从图3可以看出,不论是235U还是238U,棒平均吸收截面的相对误差在共振能区低能段比高能段大,这是因为在低共振能群,235U和238U的共振干涉效应较为强烈。此外,238U的相对误差整体上要大于235U,这说明共振干涉效应对238U的影响更大。 由图3可知,235U第25群(27.70~15.97eV)棒平均吸收截面的相对误差最大。一方面,这是因为235U第25群截面存在若干个可分辨的共振峰,有明显的共振自屏效应,而且238U第25群截面存在孤立的大共振峰,导致这2个共振核素在第25群的共振峰出现严重的相互影响。另一方面,这是由于Bondarenko迭代方法在计算一个共振核素时,假设其他共振核素的截面都不随能量的变化而变化,在处理共振干涉效应时存在一定的误差[8]。整体而言,除了235U的第25群,235U和238U各个棒平均吸收截面的相对偏差均在3.5%以内,能够保持在一个较低的水平。 表4为不同富集度下燃料栅元问题keff的计算结果,表中keff参考值由蒙特卡洛程序提供。当富集度从1.8%增大到3.1%时,有效增殖因子的计算偏差略有增大,但结果仍在可接受范围内。总体上看,本文所实施共振计算方法能够较好地处理共振干涉效应。 表4 不同富集度下燃料栅元问题keff计算结果Table 4 Calculating results of keff for fuel pin cell at different enrichment 本文选择VERA系列基准题[13]中的单栅元问题和单组件问题对HNET程序的共振计算模块做进一步验证。从文献[13]可获得基准题的几何结构及相应的材料组成,其中VERA基准题1/4组件的结构如图4所示,由燃料棒、导向管和仪表管组成。HNET程序相关计算参数的设置如下:每个卦限选取64个方位角和3个极角,单栅元问题的特征线间距为0.03 cm,单组件问题的特征线间距为0.05 cm。 图4 VERA基准题1/4组件结构Fig.4 Geometry of 1/4 lattice for VERA benchmark 单栅元或者单组件各自的4个问题具有相同的几何结构,它们所不同的是燃料温度、慢化剂温度以及核子密度。表5和表6分别为VERA单栅元问题和单组件问题有效增殖因子的计算结果,表中keff参考值由文献[13]提供。由表5和表6可知,各基准题keff计算结果的最大偏差为109 pcm,总体上计算结果与参考值相符。 表6 VERA单组件问题keff计算结果Table 6 Calculating results of keff for VERA lattice problems 图5显示了基准题2B中1/8组件归一化功率相对误差绝对值的分布情况,功率分布的参考值由文献[13]提供。由图5可知最大相对误差绝对值为3.424%,且误差较大的燃料棒主要分布在组件外围。整体上归一化功率的平均相对误差为0.925%,功率分布的误差在可接受范围内。综合有效增殖因子和功率分布可知,在典型压水堆常规问题上,HNET程序的共振计算模块具有较高的计算精度。 图5 基准题2B归一化功率的误差Fig.5 Error distribution of normalized pin power of Problem 2B 1)针对所研究的单共振核素无限均匀问题,有效共振吸收截面的相对误差均小于1%,这表明优化后的帕德近似法可以保证子群参数的准确性。 2)Bondarenko迭代方法能够较好地处理不同共振核素间的共振干涉效应。 3)通过典型基准例题的计算分析,验证了有效增殖因子和归一化功率的准确性。这表明优化后的子群方法在保证计算效率的前提下,具有较高的计算精度,适用于典型压水堆常规问题。1.2 子群固定源方程优化

2 数值验证
2.1 无限均匀问题



2.2 燃料栅元问题

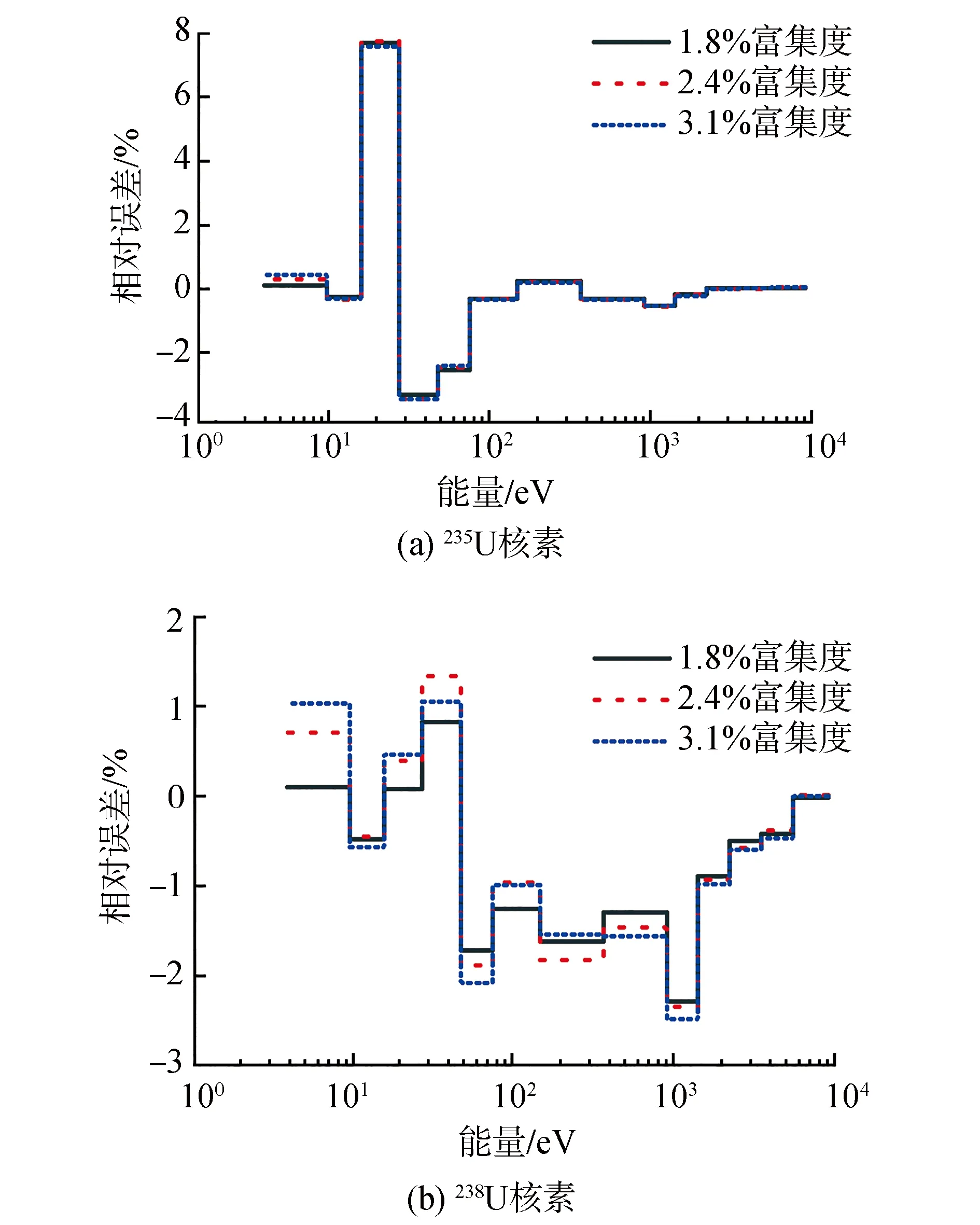

2.3 VERA基准题


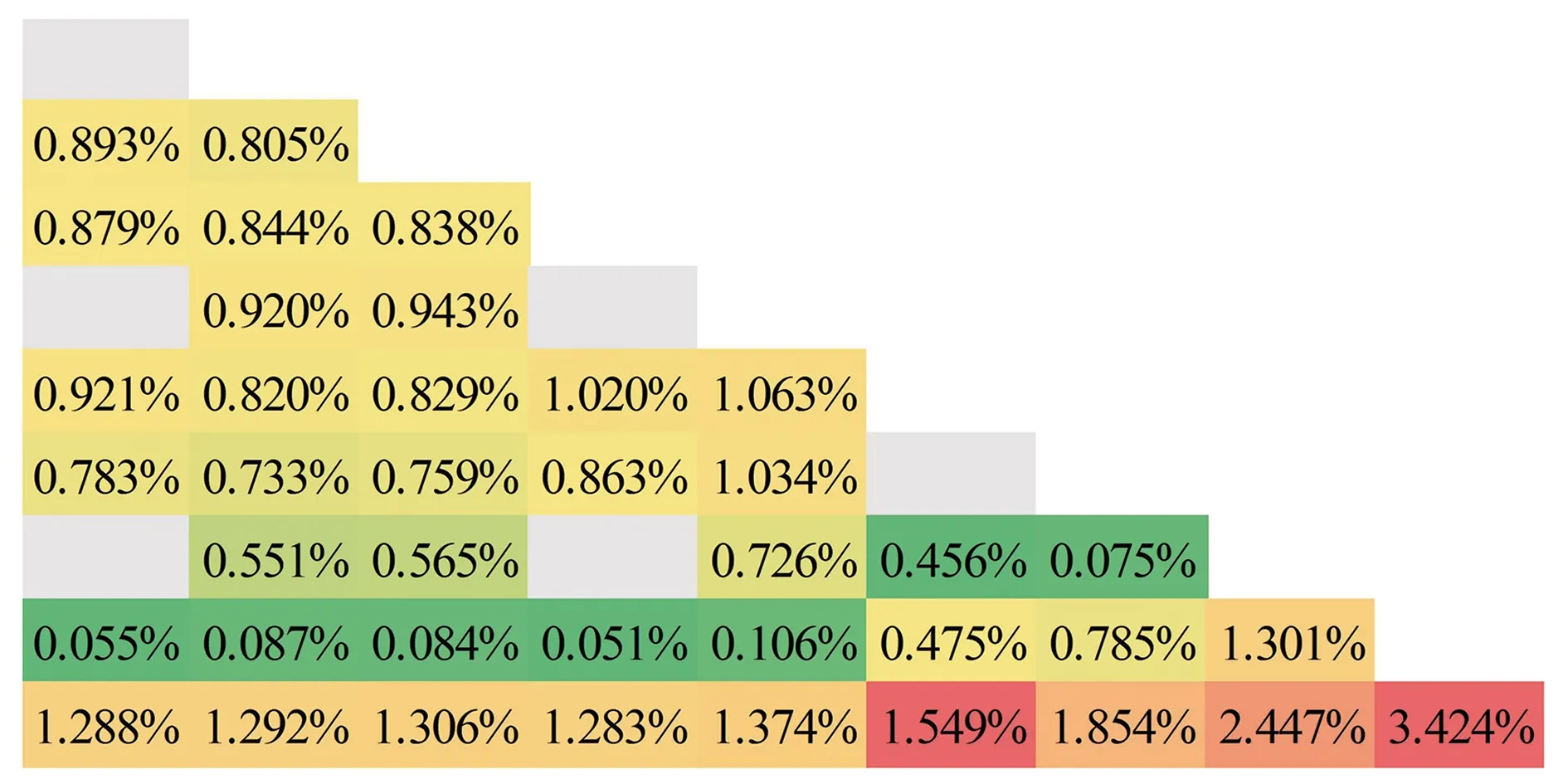
3 结论
