挖掘意外高效用项集的有效方法
2023-06-01姚银凤胡克勇
王 斌,姚银凤,周 伟,胡克勇
(青岛理工大学信息与控制工程学院,山东 青岛 266000)
1 引言
频繁模式挖掘(Frequent Patterns Mining,FPM)[1]作为关联规则[2]的一种具有代表性的方法,它因能够有效的找到模式之间的关系而被应用于各种现实问题。然而,传统的频繁模式挖掘[3]有一定的局限性。数据库项目不仅包括频率,还包括真实世界中的独特利润,这意味着频繁的模式挖掘不能反映现实世界的问题[4]。例如,数据库中有由钻石和杯子组成的事务。杯子比钻石有更高的频率,但钻石的利润高于几万个杯子,即钻石比杯子更有价值。为了克服这一缺点,提出了高效用项集挖掘(High Utility Itemstes Mining,HUIM)[5]。HUIM是一种流行的数据挖掘方法,用于发现客户事务数据库中的有用模式。它包括发现产生高效用(高利润)的项集,即高效用项集(HUIs)。除了客户交易分析外,HUIM在其它领域也有应用,如点击流分析和生物医学[6]等。HUIM可以看作是频繁项集挖掘问题的扩展,其中单位利润可以分配给每一个项目。然而传统的高效用项集挖掘在计算上具有很大的挑战性,这是由于其缺乏传统的频繁项集挖掘中的反单调特性。传统的HUIM算法还会产生大量的模式,对于用户来说分析大量的模式是困难和耗时的。此外,随着发现的模式的增多,HUIM算法的运行时间会变长,消耗的内存也越来越多。因此,高效的HUIM算法需要设计新的数据结构来提高算法性能。近年来提出的HUI-Miner算法[7]采用了效用列表的数据结构,一定程度提高了运行效率,但由于传统的效用列表占用内存过大,不适用于大型的数据集。最近提出的ULB-miner算法[8]采用了效用列表-缓冲区结构,能够有效地存储和检索效用列表,但随着大量模式的产生也会导致运行时间长及内存消耗大等问题。因此,有必要寻找一个更小的集合来挖掘高效用项集。
本文提出了一种挖掘意外高效用项集的算法,使用的UHUI-list数据结构能更加紧凑的存储项集的有效信息,并通过列表的重构及相互结合来进行挖掘工作。本文提出的UHUI-Prune策略能够有效减少搜索空间,最终寻找到特定子组中所有有意义的高效用项集。最终实验结果表明该算法性能优于当前先进的算法。
本文第2节介绍了的问题定义;第3节主要介绍了UHUI-list的构造和剪枝策略;第4节介绍了提出的UHUIM算法;第5节在真实数据集上进行实验并对结果进行分析;第6节进行总结与展望。
2 问题定义
本文目标是在表格式多维数据的事务维度子组中挖掘意外高效用项集。在本节中介绍意外[9]项集(Unexpected Itemsets, UI)及意外高效用项集的相关问题定义。
2.1 意外项集相关概念
多维表格数据集D由一组元组(也称为行或事务)组成,其中每个元组t都有一列称为唯一的元组ID(由TID表示),其它则是称为属性的列(由A={a1,a2,…,an}表示)。每个属性ai都有其值域Rg(ai),见表1。
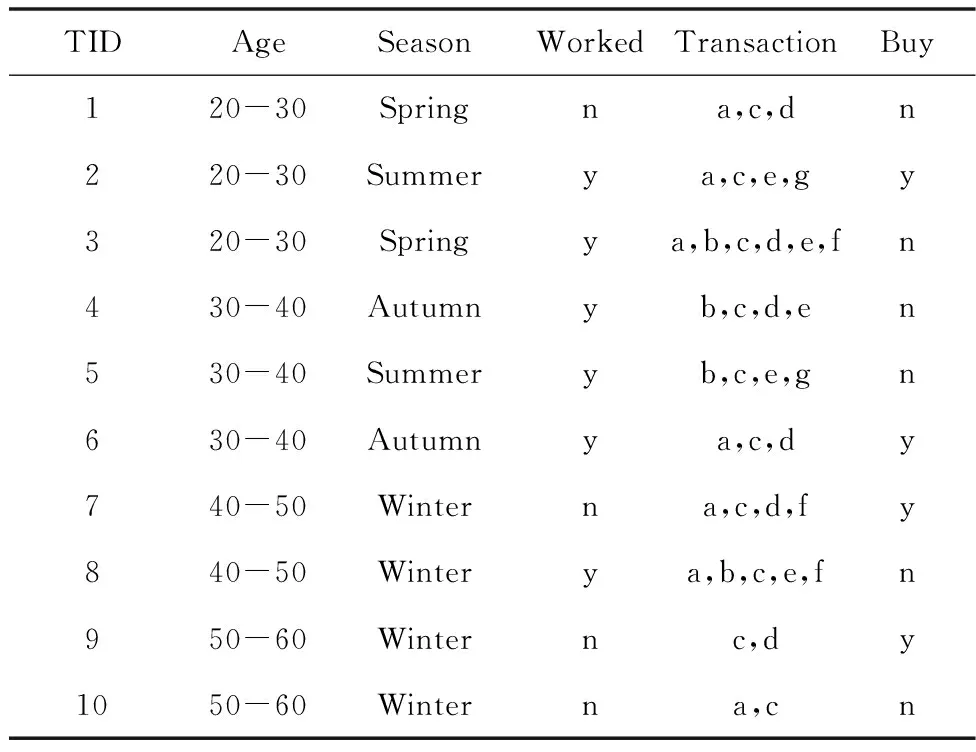
表1 某商品购买实例(其中n=no,y=yes)
D的多维项是一对(ai,vi)对,其中vi是Rg(ai)中可能的值。由Im表示的m级多维项集,它不包含重复属性。从形式上讲,有
Im={(ai1,vi1),…,(aim,vim)}
(1)
D上的多维项集Im的支持度被定义为包含Im的D中元组的百分比。例如,表1中多维项集I0={(season,spring)}的支持度为sup(I0)=0.2。下面需要研究D的切片上多维项集的支持度。给定用户指定的最小支持度阈值min_sup,如果sup(Im)>min_sup,则多维项集Im在D上是频繁的。
定义1:D的子组定义为k个多维对的结合,即S(k)={(ai1,vi1),…,(aik,vik)},子组中的属性值称为固定属性值(FVs)。
定义2:给定固定的k个属性值,通过S(k)中指定的多维对对D执行关系选择来获得S(k)的切片[10]。切片中非固定的属性值称为可变属性值(VVs)。
slice(S(k))=σ(S(k))
(2)
例如表1的子组S(1)={(season=winter)}的切片为一个包含TID={7,8,9,10}4个元组的子集,见表2。

表2 S=(season=winter). winter是一个FV
给定一个子组S(k),在后续对多维项集Im的探索中,不进一步考虑S(k)中的FVs。为简单起见,将在余文用S表示一个子组。
子组的覆盖范围为切片中的元组在整个数据集D中的百分比,表示为
cov(S)=|slice(S)|/|D|
(3)
如果一个子组的覆盖范围不小于最小阈值min_cov,则该子组是重要的。如果不存在满足S⊂S′的重要的子组S′,则S是最大的重要子组。
定义3:给定min_sup和min_cov,数据集D上的意外项集(UI)被定义为〈子组,多维项集〉对,由
给定min_sup=0.5和min_cov=0.2,很容易看出I1={(buy,y)}在原始数据集D(见表1)上不频繁,但在子组S1={(season=winter)}的切片(见表2)上频繁。因此,
通过对D进行切片操作而获得的子集被称为参考数据集D′。
定义4:给定一个min_sup,min_cov和D′=R(S),更具体地说,D′=R(S)=slice(S)。一个D′上的意外项集(UI)由
问题1:给定一个多维数据集D,一个用户指定的子组S,两个用户指定的阈值min_sup和min_cov,在对D进行切片操作获得的D′=R(S)上找到所有意外的项集
在D′=R(S)上,S={(season=winter)}。如果在D′上再执行切片操作,取S={(worked=n)},可得D′的切片,见表3。
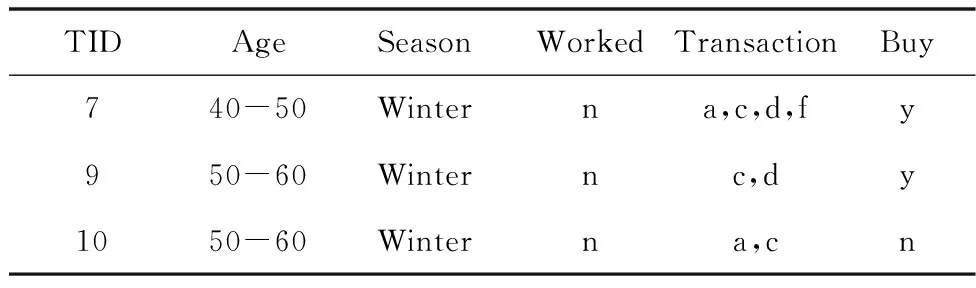
表3 D′=R(S)的切片S={(worked=n)}
2.2 意外高效用项集相关概念
本小节定义了意外高效用项集的相关术语。可见表1 中包含十个事务(Transaction,T),每个事务中包含一系列的项。其中项的频率是项的内部效用,用IU表示,见表4。项具有独特的利润,称为外部效用[11],用EU表示,见表5。
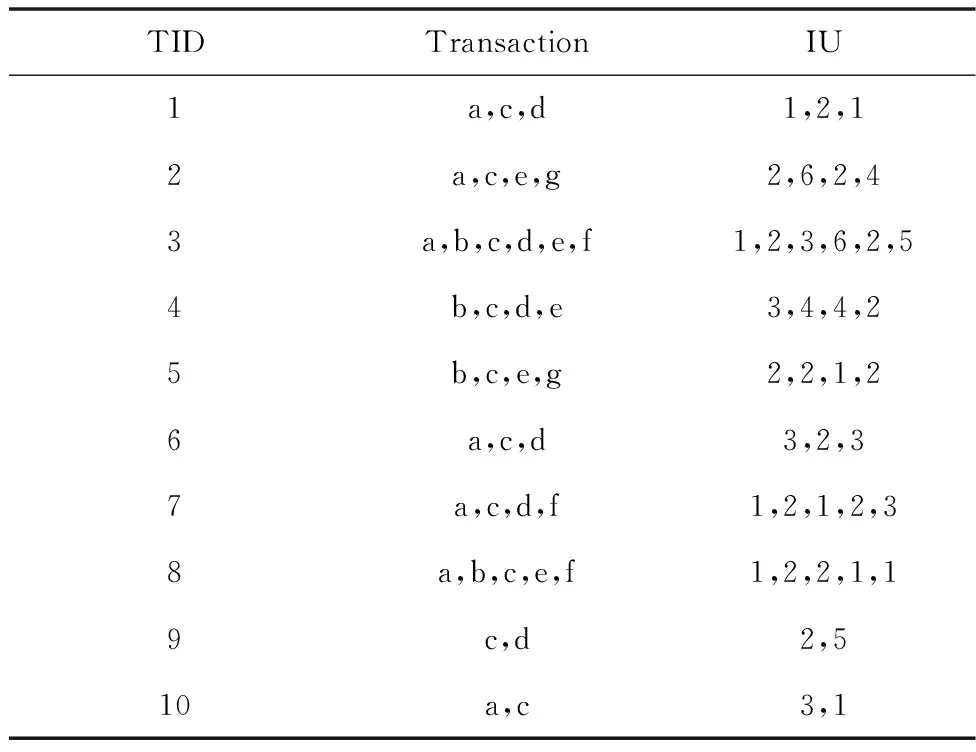
表4 运行数据集D上的事务和项

表5 项的单位利润表
在D′上,取事务一维进行挖掘,其中I={I1,I2,…,Id}是一组不同的项,事务Tj={xn∣n=1,2,3,…,Nj,xn∈I},其中Nj是事务Tj中项的数量。事务数据库D有一组事务,D={T1,T2,…,Tj},其中j是数据库中的事务总数。
定义5:xj∈Tj的效用,表示为U(xj,Tj),计算为事务中项的外部和内部效用的乘积。即
U(xi,Tj)=IU(xi,Tj)*EU(xi)
(4)
定义6:数据库中的一个子项集X的效用表示为U(X)。U(X,Tj)为项集X在事务Tj中的效用。

(5)
定义7:事务Tj的事务效用,表示为TU(Tj),定义为

(6)
定义8:项集X的事务加权效用[12]表示为TWU(X),定义为
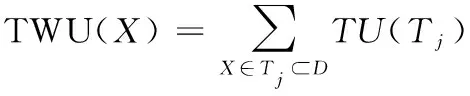
(7)
定义9:最小意外效用阈值表示为uminutil,它的计算方式为数据库D的总效用和用户定义的百分比值δ的乘积。

(8)
在本文中,表3仅包含T7,T9,T10三个事务,若给定δ=24%,则uminutil=24%*(16+18+19)=12.72。
问题2:给定一个多维数据集D,一个用户指定的子组S,三个用户指定的阈值min_sup,min_cov和uminutil,在D′=R(S)上找到所有意外的项集
定义10:如果项集X的效用大于等于最小意外效用阈值,则X为意外高效用项集,否则舍弃。
U-U(X)≥uminutil
(9)
例如,在表3中,U-U(f)=3<12.72,因此1-项集f不是意外高效用项集。
性质1:对于任意的意外高效用项集X,都存在其超集X′,使得TWU(X′)≤TWU(X)。
证明:设X′为项集X的超集,由先验属性[6]知
sup(X′)
∵U(X′)
得证。
性质2若项集X不是意外高效用项集,则其超集X′也不会是意外高效用项集。
证明:略。
3 基于UHUI-lists的UHUIs挖掘
本节介绍提出的UHUI-list数据结构以及UHUI-Prune策略来更有效地挖掘意外高效用项集。
3.1 UHUI-list的组成及构造
本文提出了一个新的数据结构UHUI-list来更紧凑的存储有效的项集信息,该列表包含一系列元组,一个元组包含了该项集所存在的事务的信息。利用UHUI-lists来挖掘意外高效用项集。
3.1.1 相关概念
定义11:在一个事务Tj中,最大效用就是事务T中所包含的项效用的最大值,记为umax(Tj)。
umax(Tj)=max({u(xi,Tj)|xi∈Tj})
(10)
定义12:对于项集X,包含X的所有事务的最大效用之和称为效用上限[13],记为uUB(X)。

(11)
定义13:事务Tj中项集X的剩余效用[14]记为RU(X,Tj)。
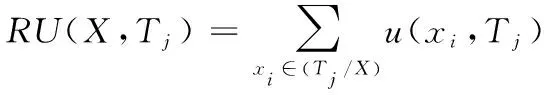
(12)
其中Tj/X表示为在事务Tj中位于项集X后的所有项的集合。例如,在表3中,RU(ad,T7)=3。
数据库D中项集X的剩余效用记为:RU(X)。
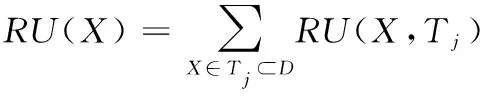
(13)
3.1.2 UHUI-list构造过程
项集X的UHUI-list记为UL(X),由UL(X).TWU和n个UL(X).tuplen两部分组成。UL(X).tuplen由以下三部分组成:事务标识符TID;项效用U,表示为UL(X).tuplen.u;剩余效用RU,表示为UL(X).tuplen.ru。UHUI-list的创建过程如下:
1)扫描D′的切片S={(worked=n)}并读取第一个事务T7。由表3可知,T7={a,c,d,f},从a项开始创建UL(a)。RU值初始化为0。将UL(a).tupleT7附加到UL(a),UL(a).tupleT7可表示为<7,5,0>。然后以同样的过程创建UL(c)等;
2)按照上述过程依次对T9,T10创建UHUI-list,直至所有事务的所有项构建完,见表6。

表6 构建UL(a)、UL(c)和uUB表
3)对所有的事务中的各项创建完UHUI-list之后,由定义8可得a、c、d、f的TWU值,由定义12可得uUB表。见表6。
3.1.3 UHUI-list重构
UHUI-list创建完成后,重构过程如下:
1)对上述创建UHUI-list的所有项按照uUB升序排序,结果为:f≻d≻a≻c,根据uUB升序对表3重新进行排序,见表7。

表7 按uUB升序排序后的S={(worked=n)}
2)由f≻d≻a≻c的最后一项c开始重构UHUI-list,由表7可重新计算RU值。在此过程中,各项的TWU值不变。RU值计算完成后,重构过程结束,见表8。

表8 重构的UL(a)、UL(c)和uUB表
3.2 剪枝策略及挖掘过程
当前的UHUI-lists包含按照uUB升序排序的1-项集,挖掘过程从含有最小uUB值的UHUI-list开始。
3.2.1UHUI-Prune策略
本文提出UHUI-Prune策略,即在用户定义固定属性值下得到的意外高效用项集的数据集DU上进行剪枝,该策略主要分四步进行剪枝:
剪枝1(U-TWU剪枝)在数据集DU上,若TWU(X)
剪枝2(U-uUB剪枝)在数据集DU上,若uUB(X)
剪枝3(U-EUCS′剪枝)在数据集DU上,若EUCS(X)
剪枝4(U-U剪枝)在数据集DU上,若RU(X)+U(X)
由UHUIs定义以及上述剪枝可知d,f两项不是UHUIs,由于d,f不满足U-TWU剪枝,故其扩展项有可能为UHUIs,但f项满足U-uUB剪枝,故剪枝掉f项。
3.2.2 从UHUI-lists中挖掘UHUIs
下面介绍UL(Xi)相互结合的过程步骤:假设重构后的项集排序为:X1≻X2≻X3≻…≻Xi。
1)检查X1是否为意外高效用项集,如果U(Xi)≥uminutil,则Xi为意外高效用项集;
2)检查X1的超集是否为意外高效用项集:若TWU(X1)≥uminutil,则X1的超集可能为意外高效用项集。经U-TWU剪枝策略过滤后,将剩下的项进行U-uUB剪枝,若uUB(X1)≥uminutil,则继续对X1进行挖掘;
3)对X1进行列表结合。首先与下一项X2进行结合产生X1X2,具体结合过程如下:先将UL(X1)与UL(X2)中具有相同TID的元组进行结合。假设X1和X2出现在同一个事务Tm中,则生成一组列表UL(X1X2).tupleTm;其次UL(X1X2).tupleTm.u的计算分为两种情况:
第一种,如果X1X2没有共同前缀,则
UL(X1X2).tupleTm.u
=UL(X1).tupleTm.u+UL(X2).tupleTm.u
(14)
第二种,如果X1X2有共同前缀X0,则
UL(X1X2).tupleTm.u=UL(X1).tupleTm.u
+UL(X2).tupleTm.u-UL(X0).tupleTm.u
(15)
接下来UL(X1X2).tupleTm.ru的计算如下
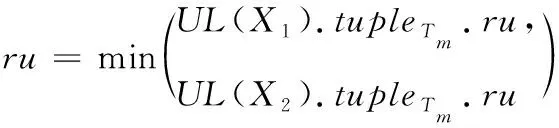
(16)
并对于X1X2的每个元组都执行上述过程;最后计算UL(X1X2).TWU:X1X2的TWU值为其所在共同事务中的事务效用之和;
4)在将两个UHUI-lists的元组组合起来后,下面将计算X1X2是否可扩展挖掘:先计算U-U(X1X2),如果U-U(X1X2)≥uminutil则X1X2为意外高效用项集;其次若EUCS(X1X2)≥uminutil,则X1X2的超集可能为意外高效用项集。
从X1到Xi重复上述所有过程以进行UHUI-lists的结合。如果生成具有前缀X1组合的UHUI-lists,则对这些组合的UHUI-lists执行挖掘过程,运用剪枝4:U-U剪枝。这个过程将递归地重复,直到基于最后一个项集的组合过程结束。最终挖掘结果为:{d},{dc},{dac},{a},{ac}和{c}为意外高效用项集。部分结果见表9。

表9 UL(dc)及UL(dac)
4 UHUIM算法
本节介绍UHUIM算法的伪代码。对于D的任何给定的切片,用(S,I)all表示切片S上所有意外项集的集合。
Algorithm 1(UHUIMmainalgorithm)
1)K=1
2)生成候选的1-Mitemsets集合I-1
3)基于I1生成重要的1-subgroups集合S1
4)Repeat
5)Sk+1=∅
6)for all significant k-subgroup S∈Skdo

8)Sk+1. add All(Snew)
9) K=k+1
10)untilSk=∅
11)kmax=k-1
12)for k=kmax-1 to1 do
13) for allsignificant k-subgroupS∈Skdo
15)∀I ∈(S,I)all,return (S,I) as 意外项集
16)将(S,I)存入集合(S,I)all中 ∥(S,I)all用于保存所有的意外项集
17)Generate_UHUIs((S,I)all,uminutil);∥生成意外高效用项集
18)End
Algorithm 2 (Generate_UHUIS)
Input:所有的意外项集(S,I)all
用户指定的最小效用阈值uminutil
Output:A list of unexpected high utility itemsets
A set of UHUI-lists of
1-length itemsets,UHUI-lists
2)A set of unexpected high utility itemsets,Result-Set
3)A table of upper bound of
1-length itemsets, uUB
4)Foreach 意外项集(S,I) ∈(S,I)all
5)For each 事务Transaction∈(S,I)
6)Foreach i in Transaction
7)If i not in UHUI-lists
8) insert i into UHUI-lists
9) Else
10) Update entry of I in UHUI-lists ∥更新UHUI-list
11) Calculate umaxof T and update uUB
12)Restructure(UHUI-lists, uUB)∥重构UHUI-lists
13) If user requests mining ∥如果用户请求挖掘
14)Mining(NULL,UHUI-lists,uminutil,Result-Set)∥执行挖掘操作
15) Return Result-Set∥返回意外高效用项集
5 实验
在本节中,评估了该挖掘方法的性能。为了客观地比较方法,UHUIM算法与当前最先进的两个算法ULB-Miner以及HUI-Miner进行对比评估。
5.1 实验设置
所有的算法都是由Java编程语言实现的。PC环境包括32GB内存、4.00GHzCPU和Window10(64位)操作系统。本文在3个真实数据集上评估三个算法的运行时间、内存使用及可伸扩展性性能。所有数据集均可从SPMF库[15]下载。数据集特征见表10。

表10 数据集特征
5.2 对运行时间性能的评估
本节比较了UHUIM,ULB-Miner及HUI-Miner三种算法在3个真实数据集上的运行时间性能。对于小型稠密的数据集chess,当uminutil为3500000左右时,UHUIM算法比ULB-miner算法的运行时间快一个左右数量级,当uminutil越小,运行时间越长。实验结果表明,3种算法的运行速度由快到慢为:UHUIM>ULB-Miner>HUI-Miner。见图1(a)-(c)。

图1 在不同uminutil值下的运行时间性能
5.3 对内存使用性能的评估
本小节对三种算法进行内存性能评估。大中型数据集chainstore及connect高于chess的内存使用。对于chainstore,在uminutil=1000000时,ULB-Miner算法比UHUIM算法的内存使用多大约5倍,HUI-Miner算法使用内存约为UHUIM算法的3.7倍。实验结果表明,UHUIM算法的内存消耗低于其它两种算法。见图2(d)-(f )。

图2 在不同uminutil值下的内存使用性能
5.4 对可伸缩性的评估
由图1、2可知,UHUIM算法在大小不同的3个数据集上运行时间差别不大,内存性能也高于其它两个算法。因此,UHUIM算法在各个数据集上的可伸缩性均优于ULB-Miner算法及HUI-Miner算法。
6 结束语
本文提出的UHUIM算法能够有效的挖掘意外高效用项集,给经营者带来意想不到的利润。本文采用新提出的UHUI-list结构更紧凑的存储项集信息,节省时间与空间。本文提出的UHUI-Prune策略能够有效的减少搜索空间,提高挖掘效率。经过在3个真实数据集上进行运行时间、存储空间及可伸缩性的实验评估,结果表明本文提出的UHUIM算法性能优于ULB-Miner算法及HUI-Miner算法。
在未来的工作中计划调整UHUI-list为UHUI-list-缓冲区结构,并研究在动态数据库中挖掘意外高效用项集的有效方法。
