基于子组行为关系的过程模型修复

李丽，方贤文

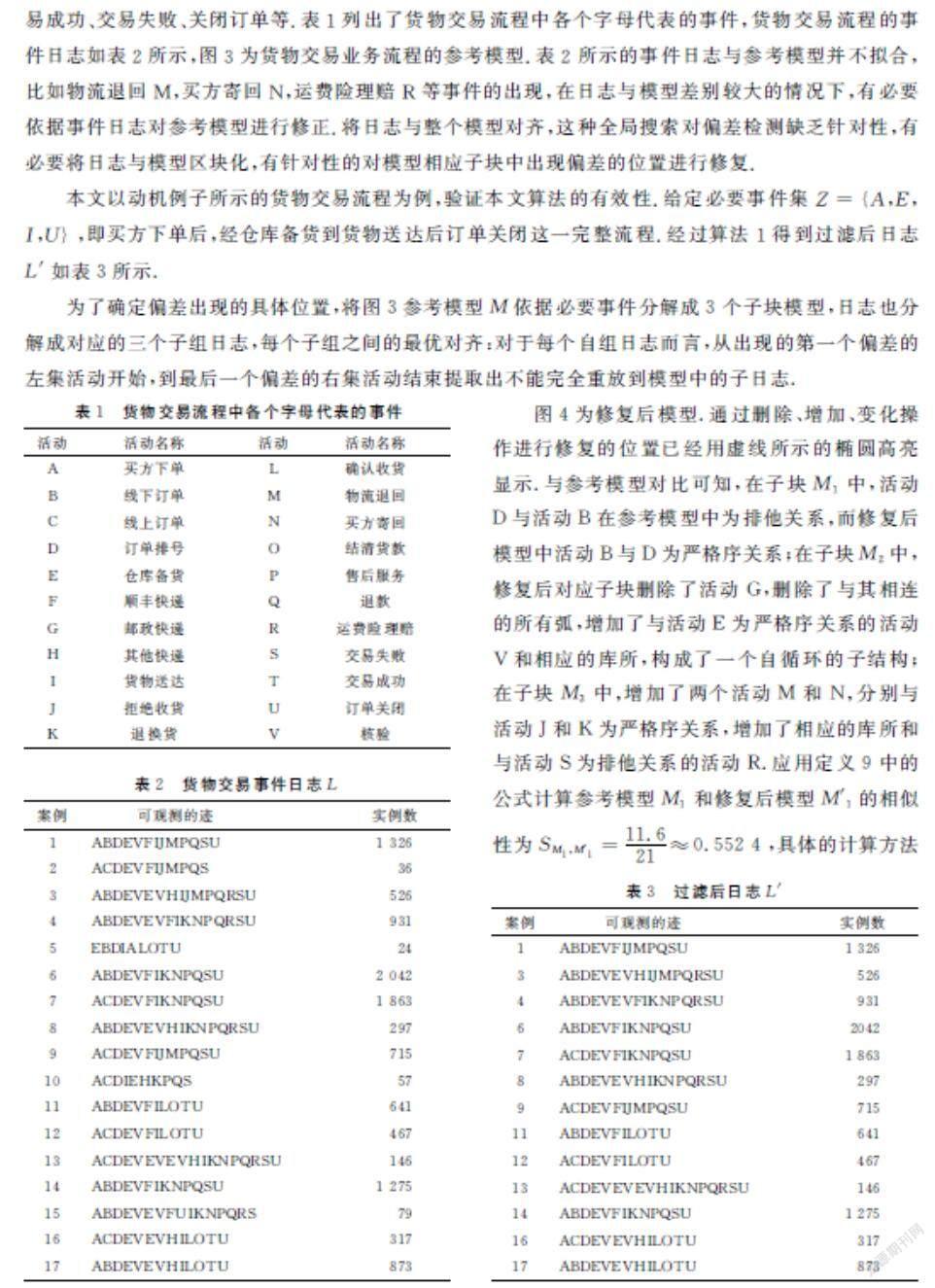
摘要：提出基于子组行为关系的模型修复方法.依据必要事件保序对日志进行过滤，将日志与模型分解成子组日志和模型子块;基于最优对齐提取子组日志中不拟合的子日志，分析子日志活动间行为关系;对于增加、删除的行为关系，在子块中插入、删除活动及相应的弧和库所;对于发生变化行为关系，在子块中改变相应的弧以支撑新行为.

关键词：模型修复;行为关系;子组;块结构

[中图分类号]TP301[文献标志码]A

Process Model Repair Based on Subgroup Behavior Relationship

LI Li，FANG Xianwen

（College of Mathematics and Big Data，Anhui University of Science and Technology，Huainan 232001，China）

Abstract：A model repair method based on subgroup behavior relationship is proposed.Filter the log according to the necessary event sequence，and decompose the log and model into subgroup logs and model sub blocks.Based on the optimal alignment，the non fitting sub logs in the subgroup logs are extracted，and the behavior relationship between sub log activities is analyzed.For the behavior relationship of adding and deleting，insert and delete activities and corresponding arcs and place in sub blocks.For changing behavior relationships，change the corresponding arc in the sub block to support the new behavior.

Key words：model repair;behavior relationship;subgroup;block structure

现代过程感知信息系统可以使用参考模型驱动软件工程方法设计.设计的参考模型在实际系统中很难精确实现，流程往往在系统的生命周期中发生变化，人们需要最新的描述流程的模型，通过分析系统的事件日志研究系统的真实行为，从而得到最符合真实流程执行的模型.Vander A H[1]等引入了一种能够处理不确定映射的概率一致性检查技术，通过考虑所有可能的映射，避免了选择单一映射的需要，解决了由于特定映射的使用直接影响到规范事件迹的一致性检测的问题.如果现有的流程模型不符合实际情况，原则上可以使用流程发现来获得符合实际情况的模型.Fahland D[2]认为，发现的模型很可能与原始模型没有相似之处，因此，对已有相关方法对模型进行修复，以得到更加完善的模型.王媛媛[3]等利用已有的一致性检测技术计算最优校准，通过标识所在库所定位偏差位置，解决现有模型修正方法仅考虑拟合度而忽略精确度以及简洁度等指标的问题.Zhang X[4]等通过LPN构建流程模型，研究选择结构中变迁之间的关系，以确定修复模型的位置，提出一种基于逻辑Petri网（LPN）的模型修复方法.Leemans S[5]等基于模型的块结构引入对不完备性不太敏感的概率行为关系，研究日志的不完备性对过程发现技术中经常使用的行为关系的影响.Y Xu[6]等考虑新活动与原始活动之间的关系，定义了新活动和原始活动间的逻辑并发关系和因果关系，构造梯形矩阵检测偏差，添加新活动与原活动构建并行关系，或插入原活动后构建因果关系实现对模型的修复.范涛和方贤文[7]利用因果关系矩阵进行过程挖掘，所得过程模型与事件日志的符合度更高.现有的模型修复方法基本是单线程从全局上进行修复，对检测的偏差位置与待修复区域之间的对应性考虑较少.本文依据必要事件保序，将模型和日志分解成子块模型和子组日志，基于最优对齐定位模型偏差位置，在对应模块中，多线程同时执行模型修复工作.实验分析结果显示，本文基于块结构多线程的模型修复工作较传统的单线程修复效率更高.

1基础知识

定义1标签Petri六元组LN=（P，T;F，ΦP，M0）称为一个标签Petri网，满足下列条件：P表示库所的有限集合;T表示变迁的有限集合;F（P×T）∪（T×P）为流关系，即有向弧的集合.L：T→Φ∪{ε}是标签映射函数，Φ为活动标签的集合.Petri网是一个包含库所和变迁的二部图，由有向弧相互连接，记为N=（P，T;F）.

定义2工作流网（WFN） 工作流网是一个具有一个起始库所和一个结束库所的Petri网，用来表示建模进程的开始和结束状态，其结构特性便于业务流程分析.工作流网所有节点都位于从开始到结束的一条有向路徑上.块结构工作流网是一个可以递归地划分为具有单个入口和出口子网的层次化工作流网.如图2中（c）流程可以划分为图1所示块结构工作流网的两个子网.

定义3迹、日志设流程活动的集合为A，事件e是指一个活动的发生，e∈A.迹σ可能是一个空的事件序列，用ε表示迹为空，有σ∈A*.日志L是一个有限非空的迹集合，用LA*表示.

定义4弱序关系设S=（N，M0）是一个网系统，其中，N=（P，T;F）为一个petri网，初始标识为M0.变迁对（t1，t2）∈（T′×T′）满足弱序关系，当且仅当存在一个由网系统N在初始状态M0下触发得到的执行序列σ=t1，t2，…，tn，即N（N，M0）[σ︿ ，且对于j，k∈N，1≤j≤k≤n，有tj=x，tk=y.

定义5[2]行为轮廓设S=（N，M0）是一个网系统，其中，N=（P，T;F）为一个petri网，初始标识为M0，任意的变迁对（t1，t2）∈（T×T）满足下面关系之一：

（1）若t1t2且t2/ t1，则称t1和t2为严格序关系，记作t1→t2;

（2）若t1/t2且t2t1，则称t1和t2为严格逆序关系，记作t1→-1t2;

（3）若t1/t2且t2/ t1，则称t1和t2为排他序关系，记作t1+t2;

（4）若t1t2且t2t1，则称t1和t2为交叉序关系，记作t1‖t2;将所有关系的集合叫做网系统的行为轮廓，记作BP={→，→-1，+，‖}.图2所示的流程（a）中，活动X和活动Y之间是严格序关系，那么，活动Y和活动X之间就是严格逆序关系.在流程（b）中，活动X和活动Y之间为排他序关系，那么，活动X和活动Y不会同时出现在同一条迹中，说明活动X和活动Y之间为选择发生关系.在流程（c）中，活动X和活动Y之间为交叉序关系，那么，活动X和活动Y同时出现在同一条迹中，但活动X和活动Y之间的发生顺序不唯一.

定义6必要事件依据活动对业务流程运行的影响程度以及考虑整个业务流程的完整性，将活动分为必要事件活动和一般事件活动.必要事件活动是指在业务流程运行过程中一定会发生的事件活动，必要事件之间的相对发生顺序始终保持一致;一般事件活动指在流程运行过程中可以选择发生的事件活动.

定义7[7]左集和右集设六元组WFN=（P，T;F，Φ，L，M0）为一个工作流网，TP为WFN中所有执行路径，对于a，b，c∈T，若存在σ=（…，ti-1，ti.ti+1，…）∈TP，使得ti-1=b，ti=a，ti+1=c，那么，b称为a的左集活动，c称为a的右集活动.a的所有左集活动称为a的左集La，类似的有，a的所有右集活动称为a的右集Ra.

定义8[11]最优对齐最优对齐是迹与模型中从初始状态到终止状态的所有完整路径进行对齐，基于成本函数下，将具有最小对齐成本的对齐结果称为最优对齐.设σ∈A*，且LN=（P，T;F，Φ，L，M0）为一个Petri网，γ∈（a>>，tτ >>）*是迹σ与LN网的一种对齐，在成本函数c的情况下，对齐成本为C（γ）.其中，C（γ）=∑|γ|-1i=0c（γi）.γopt为最优对齐，当且仅当任意的对齐结果的成本都大于等于最优对齐，即C（γopt）≤C（γ）.其中，C（γopt）表示最优对齐成本.

定义9[7]相似性令W1，W2为两个工作流网，若ti∈T1∧ti∪T2，则W1，W2关于活动ti的相似性SW1，W2（ti）=a·LW1ti∩LW2tiLW1ti∪LW2ti+β·RW1ti∩LR2tiRW1ti∪RW2ti，那么，流程模型之间的相似性为

SW1，W2=∑ti∈T1∩T2SW1，W2（ti）max‖T1|-2|，‖T2|-2|.

2基于子组行为关系的模型修正

本文提出基于子组行为关系的模型修复，将整个流程模型以必要事件为界限分解成几个块结构的子模型，对应地将事件日志以必要事件为界限分解成几个子组日志，然后将子组日志重放到子块中，提取出不能完全重放的子日志.分析子日志中活动间的行为关系，将新的行为关系取代参考模型中活动间的行为关系.依据更新后的子组行为关系，在对应子块的相应位置，对模型进行插入、删除、改变操作进行修复.

必要事件按照一定的顺序发生，从粗粒度的角度看整个流程执行，反映了整个流程的完整性.记录：日志中流程实际执行数据，会出现与参考模型不完全一致的情况，如插入新活动、删除一些原活动以及改变原来活动间的行为关系等.算法1描述了依据流程中必要事件间的保序过滤事件日志，以必要事件集合Z和日志L作为算法输入，对于日志中的每一条迹，依次访问迹中的每个活动，按顺序存储搜索得到必要活动集合Z′，直至迹中的最后一个活动（算法1中1～3行）;比较搜索得到的必要事件个数、元素以及它们间的相对顺序.当搜索得到的必要事件个数|Z′|与给定必要事件集合个数|Z|不一致时，直接抛弃当前迹;当|Z′|=|Z|时，比较集合Z中元素与Z′中元素是否相同，若不相同则抛弃当前迹，若相同则比较必要事件集合中事件间的相对顺序，若相对顺序保持一致则保留当前迹，反之则抛弃当前迹（算法1中4～9行）.

为了能够更有针对性地找到日志与模型中出现偏差的位置，根据必要事件集Z，将参考模型M和由算法1得到的过滤后日志L′分解成模型子块Mi和子组日志L′i，并提取模型子块活动间行为关系Bi（算法2中1～5行），将子组日志L′i与相应的子块Mi分别对齐.基于最优对齐，从出现的第一个偏差的前集活动到最后一个偏差的右集活动提取出子组日志中不能完全重放的子日志L″i，并分析得出活动间行为B′i（算法2中6～12行）.

利用算法2得到的子行为关系B′i，与模型子块活动间的行为关系Bi之间存在差别.算法3描述了依据子组行为关系对参考模型进行修复.以行为关系Bi和B′i作为输入，比较Bi和B′i中保留相同的活动间行为关系.若活动间关系发生变化，将B′i中的关系替代Bi中对应的关系，在模型中的对应子块中，对于发生变化的行为关系，删除维持原行为关系的弧和变迁库所，插入支撑新行为关系的弧和变迁库所（算法3中1～7行）;若B′i中出现的新的行为关系b′k，合并到Bi中，在对应子块模型中插入相应的活动和连接活动的弧（算法3中8～10行）;若Bi中存在B′i中没有出现的行为关系bk，从Bi中删除，在模型的对应子块中，删除相应活动和连接活动的弧，最终得到一个新的子组行为关系B″i和修復后的模型M′（算法3中10～15行）.

3实例分析与实验仿真

随着电商行业的崛起，传统的货品交易流程在一定程度上发生了变化.货物交易业务流程主要包括以下步骤：买方下单、订单排号、仓库备货、选择快递发出、货物送达、确认收货、退换货、结清货款、交易成功、交易失败、关闭订单等.表1列出了货物交易流程中各个字母代表的事件，货物交易流程的事件日志如表2所示，图3为货物交易业务流程的参考模型.表2所示的事件日志与参考模型并不拟合，比如物流退回M，买方寄回N，运费险理赔R等事件的出现，在日志与模型差别较大的情况下，有必要依据事件日志对参考模型进行修正.将日志与整个模型对齐，这种全局搜索对偏差检测缺乏针对性，有必要将日志与模型区块化，有针对性的对模型相应子块中出现偏差的位置进行修复.

本文以动机例子所示的货物交易流程为例，验证本文算法的有效性.给定必要事件集Z={A，E，I，U}，即买方下单后，经仓库备货到货物送达后订单關闭这一完整流程.经过算法1得到过滤后日志L′如表3所示.

为了确定偏差出现的具体位置，将图3参考模型M依据必要事件分解成3个子块模型，日志也分解成对应的三个子组日志，每个子组之间的最优对齐：对于每个自组日志而言，从出现的第一个偏差的左集活动开始，到最后一个偏差的右集活动结束提取出不能完全重放到模型中的子日志.

图4为修复后模型.通过删除、增加、变化操作进行修复的位置已经用虚线所示的椭圆高亮显示.与参考模型对比可知，在子块M1中，活动D与活动B在参考模型中为排他关系，而修复后模型中活动B与D为严格序关系;在子块M2中，修复后对应子块删除了活动G，删除了与其相连的所有弧，增加了与活动E为严格序关系的活动V和相应的库所，构成了一个自循环的子结构;在子块M3中，增加了两个活动M和N，分别与活动J和K为严格序关系，增加了相应的库所和与活动S为排他关系的活动R.应用定义9中的公式计算参考模型M1和修复后模型M′1的相似性为SM1，M′1=11.621≈0.552 4，具体的计算方法见参考文献[9].

若参考模型中平均有m个活动，平均每个活动对齐所需的时间为n，检测出所需修复偏差的个数为s，平均完成一次修复花费的时间为t，依据必要事件将模型分解成的子块个数为u，则一般单线程的修复工作所需时间复杂度为O（mn+st）.本文所提出的基于子组的多线程修复工作所需时间复杂度为Omn+stn，分解的子组个数越多，所需的时间越少，工作效率越高.

依据定义的必要事件，提出了基于模型块结构分段将事件日志与模型进行对齐，将单线程的对齐问题转换为多线程进行，在基于对齐的偏差检测阶段减少了所需时间.基于子组行为关系的模型修复工作也将以多线程代替原来的单线程工作，使修复工作更具针对性，提高了模型修复的效率.

4结束语

本文提出了基于子组行为关系的模型修正方法.笔者基于必要事件将日志转换为子组日志，将参考模型转换为对应模型子块.将子组日志与模型子块分别对齐，依据最优对齐提取子组日志不能完全重放到模型中的子日志，分析子日志中各活动间的行为关系，与参考模型对应子块的活动间行为关系进行对比，通过增加、删除、改变操作，得到新的子组行为关系.在对应子块中进行插入、删除变迁和库所及连接二者之间的弧，对模型进行修复.

参考文献

[1]Van der Aa H，Leopold H，Reijers H A.Efficient process conformance checking on the basis of uncertain eventtoactivity mappings[J].IEEE Transactions on Knowledge and Data Engineering，2019，32（5）：927940.

[2]Fahland D，Van der Aalst W M P.Model repair—aligning process models to reality[J].Information Systems，2015（47）：220243.

[3]王媛媛，杜玉越，祁宏达.基于逻辑Petri网的模型修正方法[J].计算机集成制造系统，2018，24（7）：17361746.

[4]Zhang X，Du Y，Qi L，et al.A Method for Repairing Process Models Containing a Choice With Concurrency Structure by Using Logic Petri Nets[J].IEEE Access，2019（7）：1310613120.

[5]Leemans S，D Fahland，Aalst W.Discoveonal Conference on Applications and Theory of Petri Nets and Concurrency. Springer，Cham，ring BlockStructured Process Models from Incomplete Event Logs[C]//Internati 2014.

[6]Y Xu ，Y Du，Luan W，et al.Repairing Process Models with Logical Concurrent and Casual Relations via Logical Petri Nets[J].IEEE Access，2018（99）：116.

[7]范涛，方贤文.一种基于Petri网和因果关系矩阵的事件日志过程挖掘方法[J].牡丹江师范学院学报;自然科学版，2020（4）：1014.

[8]段瑞，方欢.基于Petri网的电梯控制系统建模与分析[J].牡丹江师范学院学报：自然科学版，2018（3）：2428.

[9]李东月，方欢.基于活动发生关系的流程相似性度量方法[J].控制理论与应用，2020，37（9）：20112019.

编辑：琳莉