基于键合图的T型逆变器参数性故障诊断

樊鹏帅,帕孜来·马合木提,魏胜风

(新疆大学电气工程学院,新疆 乌鲁木齐 830046)

1 引言

逆变器在实际运行中,由于环境及内部应力的影响,元器件的标称参数会发生退化现象。当参数退化超出阈值即发生参数性故障(软故障)。此类故障发生后如果不能找出故障原因,故障会持续存在并诱发连锁效应[1]:可能使输出特性改变,影响电能质量;或演变为严重的结构性故障,造成人员伤亡和财产损失。为了确保逆变器系统的安全平稳运行,需要在严重故障出现之前对故障源进行隔离。然而参数性故障特征表现微弱,特征提取困难并且此类故障又是系统的一大安全隐患。因此,近些年对参数性故障诊断方法的研究已经成为研究热点。

三电平逆变器相较于两电平逆变器,具有较低的电压应力、高质量的并网电流及较小的电压谐波等优点,因而受到广泛应用。但随着三电平逆变器IGBT数量的增多,主电路也更加复杂且系统呈现出高非线性的特点,这不仅加大了故障出现的可能性也为故障诊断带来困难[2]。有关数据指出,在光伏电站运行过程中,逆变器系统故障比例占整体光伏电站常见故障的60%[3,4]。因此,对逆变器的故障诊断研究有着十分重要的现实意义。

逆变器主电路属于电力电子电路。目前,针对于电力电子电路的故障诊断方法多适用于结构性故障,对参数性故障诊断方法的研究相对较少,国内外的研究主要集中于拓扑结构相对简单的DC/DC电路及两电平DC/AC电路。文献[5]基于键合图理论得出电力电子电路的行为模型,实现了Buck电路的健康预测,但所研究领域局限于DC/DC电路。文献[6]基于BG理论实现了对单相全桥逆变器的故障检测和隔离,但单相全桥逆变器适用范围有限,随着系统复杂程度的加深,基于BG建模的难度随之增强。文献[7]基于解析冗余关系实现了对飞跨电容型逆变器的故障源定位,但并未综合考虑钳位电容退化下的多故障源定位问题。

本文提出基于BG理论来建立三电平T型逆变器混杂键合图模型。结合BG模型与测量信号推导出T型逆变器的GARRs,比较系统实际输出与无故障时的期望输出得到残差和一致性向量C,通过对比C与FSM实现了兼顾12个IGBT和2个钳位电容的多故障源的故障诊断。最后在20-sim仿真平台上验证了此方法的有效性。

2 T型逆变器

T型三电平逆变器拓扑结构如图1所示,其开关状态及输出电压如表1所示。

表1 开关状态及输出电压表

图1 T型逆变器拓扑结构

本文采用三角载波同相层叠PWM调制策略实现对T型逆变器的IGBT控制[8]。以三角波T1、T2作为载波,以正弦波Sine作为调制波。以A相为例,T型逆变器控制方式如图2所示。

图2 三角载波层叠调制仿真图

3 键合图理论

键合图(Bond Graph,BG),全称为功率键合图。BG理论自被提出以来,已经在电气、热力学、化学、流体、机械等工程技术领域中的动态分析与故障诊断领域得到广泛应用[9-11]。并且基于键合图的故障诊断具有建模容易、推理算法严谨且扩展性好、诊断效率高、故障隔离实施性强等优点。

BG理论核心思想是能量守恒,它能够以一种统一的方法对系统各部分能量的构成转换、相互间逻辑关系及物理特征等进行说明,从而实现对系统模型的充分且完备的定义描述[12-14]。

对逆变器这类混杂系统而言,键合图方法比一般的数学建模方法更容易、更准确,利用键合图可以建立系统的元件级模型,能够直观的阐明系统内各元件间的相互作用关系。因此,键合图建模方法也越来越多地应用于电力电子系统建模。

4 T型逆变器键合图建模

4.1 功率开关器件键合图建模

建立T型逆变器的键合图模型首先要对IGBT进行建模,IGBT是一个快切换的器件。为此本文在建模过程中引入受控结点[15,16]来对其进行描述。并同时使用布尔变量αi,(i=1,2…n,n为变量个数)用以区分结点的开关状态,当结点状态为ON时αi=1,否则αi=0。受控结点示意图如图3所示,可调转换器MTF用以接收控制信号signal。然后对IGBT进行等效电路转换[17],等效电路图如图4所示,当IGBT关断时,关断电阻为Roff=1MΩ;当IGBT导通时,导通电阻Req≈Ron·Roff/(Ron+Roff) ≈Ron=0.1Ω。由受控结点思想结合键合图理论建立IGBT键合图模型如图5所示。其中11结点为受控结点。

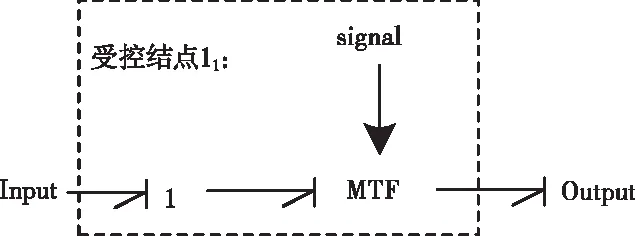
图3 受控结点示意图

图4 IGBT等效图

图5 功率开关器件键合图模型

4.2 T型逆变器键合图建模

以T型逆变器作为建模对象,由功率器件等效法结合节点[18]建模法,选取图6中O1至O9这9个节点作为0结点,建立的T型逆变器BG模型如图7所示。其中Cγi(γ∈{a,b,c,g};i∈{1,2,3,4})的取值趋于零值,它们存在的意义是作为辅助器件消除代数环,在推导GARRs时可以将其忽略,这对整个系统不会产生影响。

图6 T型逆变器节点选取图

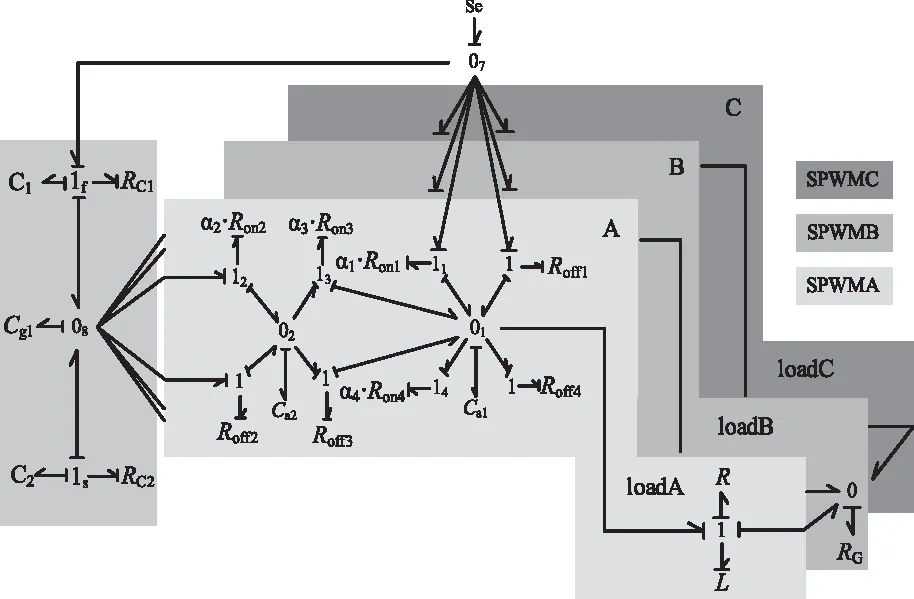
图7 T型逆变器键合图模型

仿真时直流侧输入电压设为600V,逆变器滤波前后相电压和线电压波形如图8和图9所示。

图8 A相滤波前相电压和线电压波形

图9 A相滤波后相电压和线电压波形

5 参数性故障特征分析

不同于结构性故障,参数性故障特征较为隐蔽,故障出现后虽不能使系统立即陷入瘫痪,但会使系统功能衰退陷入不确定状态,影响系统稳定,最终会逐步演化为严重的结构性故障。逆变器内部元器件发生参数性退化时主要表现形式为电容值C1、C2的减小和电容等效串联电阻Rc1、Rc2的增大;功率开关器件导通电阻Ron的增大等[19,20]。

图10～11给出了在0.02～0.07s时间段内注入参数性故障时的相电压和线电压波形与正常时的电压波形对比图。与正常波形相比,故障波形产生了微小畸变,且不同故障源故障特征区别不明显,对于此类特征,传统的故障诊断方法难以做出判断。

图10 电容故障时电压波形对比

图11 IGBT故障时电压波形对比

6 参数性故障诊断

基于键合图的故障诊断流程如图12所示。

图12 故障诊断流程

6.1 参数性故障检测

基于BG理论对系统进行参数性故障诊断时需要在键合图模型中加入势传感器De和流传感器Df来获取系统信号进而将其转化为诊断键合图(diagnosis hybrid bond graph, DHBG)。

以A相为例进行描述,首先对所有的对功率键和各个结点进行标号,然后在结点01、02、07、08处分别加入势传感器De1、De2、De7、De8,在结点1f、1s(普通1型结点)分别加入流传感器Df1、Df2。T型逆变器A相的诊断键合图如图13所示。最后在系统的B相和C相的03、04、05、06结点也分别加入势传感器De3、De4、De5、De6,用以推导能够描述整个逆变器系统内部各元器件间相互作用关系的GARRs。

图13 A相诊断键合图

6.2 全局解析冗余关系推导

GARRs是系统模型结合系统参数和测量信号推导而来,包含了系统已知条件的约束关系。当系统参数出现退化时,由约束关系就能得到系统相应变化。根据键合图元件间的因果关系和因果路径,由遍历路径法对每个结点列写本构方程[18],对于1型结点,所有键上的流变量相等,而势的代数和为零;对于0型结点,所有键上的势变量相等,而流的代数和为零。对A相进行分析说明,选定01、02、07、08、1f、1s这几个结点来推导GARRs,以01结点为例,存在解析冗余关系

f6+f7-f8-f9+f11+f12-f31=0

(1)

式中

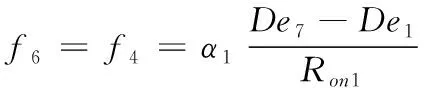
(2)

(3)

(4)

(5)

(6)

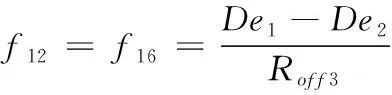
(7)

f31=0

(8)

综合(1)～(8)式,得到01节点的解析冗余关系式为式(9)

(9)

类似的,结点02、07、08、1f、1s的解析冗余关系式可以分别获得。同理,可进一步得到整个系统的GARRs。

6.3 残差与故障特征矩阵

残差r(residuals)是GARRs的数值评估结果,是由系统正常状态下的期望对比故障状态下实际输出而产生。正常状况下,r为0或趋于0。参数退化时,r做出响应不再是0。通过对r的监测,可有效检测到系统参数的变化,实现对系统的故障检测与隔离。残差数量和传感器数量一致为10个:见式(10)～(19)。

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

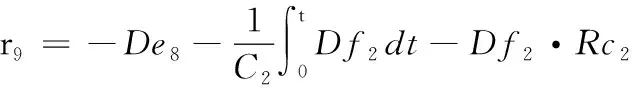
(18)

(19)

故障特征矩阵FSM反映了故障集合与残差集合的对应关系。矩阵元素由GARRs来确定,通用格式如式(20)所示。故障可检测性(fault detectability,Db)和故障可隔离性(fault isol-ability,Ib) 用{0,1}表示,当FSM行向量中至少有一个元素为1则Db=1,(即退化器件有相对应残差信号响应),否则为0;当FSM中行向量具有唯一性(即故障源可区分)时Ib=1,否则为0。系统全模式下的FSM如表2所示。由于Rc1、C1和Rc2、C2分别同时表征同一电容的健康状况,因此对应的Ib分析可将这两个参数结合起来考虑。

表2 故障特征矩阵表

(20)

式(20)中,ri:第i个解析冗余关系式,0

定义二进制相干向量C=[c1,c2,…,cn…,cm], (cn∈{0,1})来表示当前模式下的故障状态,当|r|超出阈值时cn=1,否则为0。当系统发生退化行为时,检测残差信号并生成C,匹配C与FSM的行向量,二者若一致,则准确定位到故障源θ。

7 结果分析

在20-sim平台上进行仿真验证,在0.02～0.07s时分别注入参数性故障(使Roni,i=1,2,…,12;C1、C2、Rc1、Rc1的参数退化5%),各残差响应如图14所示。

图14 系统各参数退化时的残差响应注:(a):正常情况下的残差 (b):C1、Rc1退化时的残差 (c):C2、Rc2退化时的残差 (d):Ron1、Ron5、Ron9同时退化时的残差 (e):Ron2、Ron6、Ron10同时退化时的残差 (f ):Ron3、Ron7、Ron11同时退化时的残差 (g):Ron4、Ron8、Ron12同时退化时的残差

在各元器件参数性故障未出现时,系统输出各残差均为0,对应C=[0,0,0,0,0,0,0,0,0,0]。注入故障时,相对应的r1～r9均作出响应且与FSM保持一致,以图15(b)为例说明:图15(b)对应C=[0,0,0,0,0,0,0,1,0,0] 匹配FSM将准确定位到故障源为C1、Rc1,表明是电容C1出现了参数性故障。同理,其它故障源出现时也可分别被准确定位并能够被区分开来。由此,验证了此方法的有效性。

8 结论

本文对三电平T型并网逆变器参数性故障时的特征及诊断方法进行了系统性研究。提出基于BG理论建立T型并网逆变器模型,通过结合混杂BG模型和测量信号推导出T型逆变器的GARRs,比较系统正常情况下与参数退化情况下的残差响应实现了兼顾12个IGBT和2个钳位电容的多故障源的参数性故障诊断,有效解决了T型三电平逆变器早期参数性故障诊断问题。