干法重介质流化床压力多尺度分析与流化质量表征

张赣苏 ，董 良 ，周恩会 ，周晨阳 ，段晨龙 ，赵跃民

（1.中国矿业大学 煤炭加工与高效洁净利用教育部重点实验室, 江苏 徐州 221116；2.中国矿业大学 化工学院, 江苏 徐州 221116）

0 引 言

煤炭是我国能源安全的压舱石和稳定器[1]。选煤是煤炭清洁加工利用的源头技术[2]。传统的湿法选煤技术极度依赖水资源，而我国主要产煤区域又干旱缺水，资源上的错配使得耗水量大的湿法分选技术应用受到限制[3]。同时，我国褐煤资源丰富，较低的变质程度使其具有遇水易泥化的特征。湿法带来的水分也会对严寒地区产品的装卸及运输造成困难。干法选煤是干旱缺水地区与易泥化煤炭高效分选提质的重要途径，在解决湿法技术痛点的同时，与湿法工艺联合协同发展，共同推动煤炭使用过程中的清洁高效利用。

干法重介质流化床通过上升气流驱动加重质颗粒流化形成一定密度的气固流态化床层，实现对煤炭按密度分选，床层密度均匀稳定性即床层流化质量是决定分选精度的关键。然而在分选过程中，流化床内存在大量非均匀的气泡结构，是床层密度扰动的重要来源之一[4]。附加上运动内构件、入料等多因素的综合影响，床层流化行为复杂多变，压力信号呈现出非均匀性、非线性、多尺度特征。这些多尺度的物理特征耦合在一起，以不同的权重反映于床层密度波动，最终影响着分选效率。通过测量产品灰分判定分选效果存在着一定的时间延迟，具有滞后性[5]。如果能够通过压力波动更精准地表征流化质量，就能在极短的时间尺度上实现分选密度在线调控，提高分选效率及其稳定性[6]。

现有的压力信号分析方法涵盖了时域、频域和状态空间分析[7]。然而不存在一种数据分析方法能够提取出所有的信息，只是从不同的角度对信号进行分析，从而提取出反映不同物理现象的特征量。二阶矩及高阶矩的处理能够提取波动幅度以及概率密度分布特征，但也丢失了时间尺度上的相关信息[8]。而更多的时域分析方法，如平均循环时间、概率密度函数、自回归模型参数估计、Hurst 指数分析等，存在各自适用的场景[9]。床层密度标准差仍是干法选煤工业应用中最普遍的评价密度稳定性的方法[10]。弛疏指数以及弛疏度也被引入评价干法分选效果，但缺乏一定的普适性[11]。流化质量指数被定义为平均压力振幅变化除以主频率，用来表征流化床性能。受此思路启发，将时域、频域等多种分析指数以不同的权重结合在一起形成一个混合指标，或许能够考虑到多尺度特征对于密度波动的影响，更能精准地表征流化质量。

综上所述，对干法重介质流态床的压力信号进行多尺度特征分析，建立结合时域和频域分析的混合性流化质量指标，综合评价床层均匀稳定性，为密度调控提供在线无时延且精确的目标函数。

1 试验设备与方法

干法重介质流化床试验系统如图1 所示。整个平台主要由供气系统、气流控制和调节系统、流化床分选系统，测量及采集系统组成。分选流化床是由有机玻璃制成的直径15.2 cm，高度为92 cm 的圆柱体。布风板采用烧结板，其孔径为10 μm。床层边壁均匀设置8 个测压铜管，其中最底端的铜管设置在布风板上方5 cm 处，其余测压管相邻间距为10 cm，用于采集床层密度的轴向分布特征以及稳定性。试验采用微压差传感器对床层压降进行测试，量程为0～5 000 Pa，满足采集工作的需要。为简便描述，下文把15～25、25～35、35～45、45～55、55～65 cm高度区间称为20 号、30 号、40 号、50 号、60 号、70 号，把最底端上方5 cm 处到床层顶部的高度区间称为总床层。

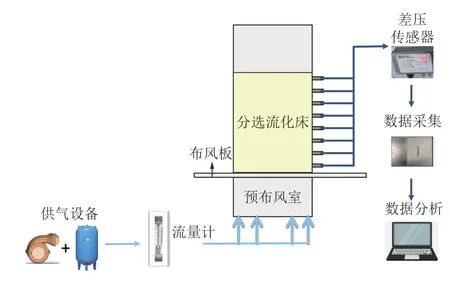
图1 试验设备示意Fig.1 Schematic of test equipment

目前，空气重介流化床选用主导粒级为74～300 μm的磁铁矿粉作为加重质。属于Geldart B 类颗粒，在煤炭的工业分选中应用成熟。但Geldart B 类的颗粒特性使得分选流化床内易兼并形成较大的气泡，严重影响了床层密度的稳定性，对操作条件存在一定的限制[12]。

探究 Geldart A 类重介质的使用可能性，具体性质见表1。展示的所有图均在静床高为70 cm 的情况下进行试验分析。

表1 颗粒参数性质Table 1 Parameter properties of particles

当流化床的横向尺度增加时，煤炭颗粒的分选并不会受到明显影响。但是随着床层高度的增加，煤炭颗粒分选效果变差，说明干法重介质流化床的压力信号具有轴向差异传递与横向等效扩散特性[13]。因此，着重研究了床层轴向压差波动特征，分析其中的多尺度特性，并对流化质量进行定量表征。

2 结果和分析

多尺度是从宏尺度、介尺度、微尺度3 个方面对系统进行分析。宏尺度指整体流化床系统的流动特征。在2.1 节时域分析中，通过总床层压降标准差反映床层密度波动，从宏观角度对流化质量进行表征。介尺度指流化床内气泡（或颗粒聚团/团聚物等）的运动行为，而微尺度指颗粒的运动。在2.2 节频域分析中，通过获取气泡运动频率（介尺度）和流化床自然振荡频率（微尺度），分析了2 个尺度对流化质量表征的影响。

2.1 时域分析

最为广泛直观且简单有效的时序分析方法是对压力信号偏离平均值的波动幅度进行定量描述。统计分析时间序列的二阶矩，如标准差和绝对平均偏差，是最主要的表征指标[14]。标准差的计算虽然简单，但也意味着数据分析并不耗时或复杂，适用于工业上的在线监测或调控，具有极强的普适性和通用性。因此，标准差的应用大体分为2 种：①流型识别，可用于最小流化速度的确定，或确定从鼓泡流态化到湍流流态化的状态转变。②流化床流体动力学的在线监测，例如确定颗粒尺寸或“流化质量”[15]。在信号处理的理想情况下，假设信号或噪声服从高斯分布，仅采用二阶矩便可提取并代表时间序列中蕴含的信息。但是现实系统中的信号，如鼓泡流化床中的压力波动，常常具有非高斯统计特性[16]。二阶统计量只表征信号中的单一信息，难以处理蕴藏在多相流系统的时间序列中的各种复杂的动态物理信息。对于非高斯信号，通常采用高阶矩，如偏度和峰度，以提取不同流型下压力信号的非高斯特性。

标准差的计算公式，如式（1）、式（2）所示：

式中：N为样本数量；x(n)为时间序列测量值；x¯为时间序列平均值：

总床层压降是气固两相流中的基本参数，是对系统流动状态的一种宏尺度描述。流化床中流动状态随表观气速而产生的各种变化，会映射为床层压降的相应变化，是合理评估床层流动状态的重要指标。在此，将布风板上方5 cm 处到床层顶部的压降近似视为总床层压降，并作出其标准差随表观气速的变化，如图2 所示。

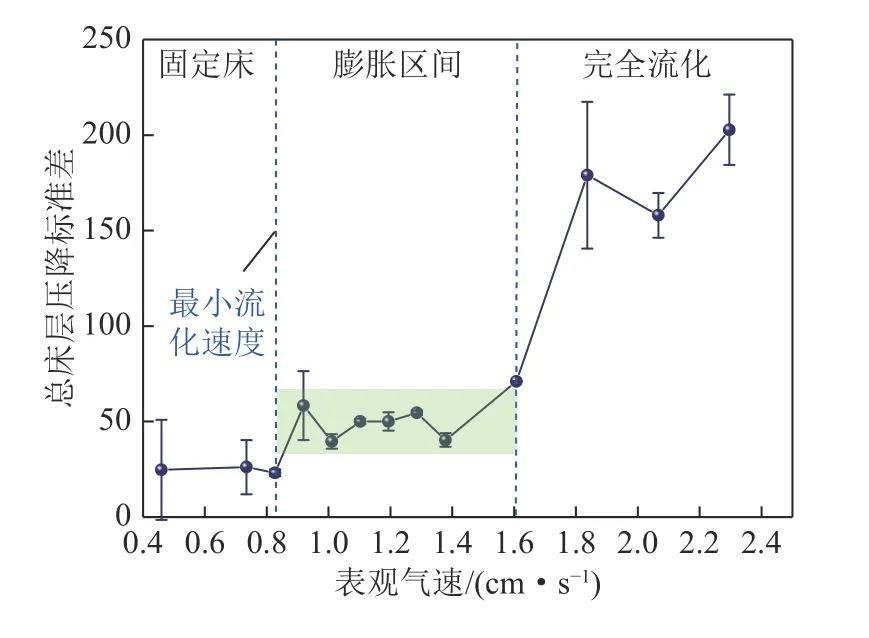
图2 总床层压降标准差随气速的变化Fig.2 Variation of standard deviation of total bed pressure with gas velocity

研究中，通过失流化试验，最小流化速度可以较为容易地确定为0.83 cm/s。而最小鼓泡速度的确定通常带有主观性与随机性，这是因为床层的非可视化特征使得难以观察到床层内部的真实情况。并且因为暂态空隙与气泡的模糊边界，气泡和无气泡系统之间的区别不是绝对的[17]。因此，最小鼓泡速度在不同研究者的眼中存在不同的定义，大体分为3种[18]。最常见的定义是基于视觉观察确定“第一个气泡”出现时的气体速度。第二个定义是基于流化床高达到局部最大值后出现收缩现象时的气体速度。第三个定义是根据关键变量（压降的标准差）发生突变时的气体速度。在此，依据第3 种定义分析总床层压降标准差的阶跃变化，对流态进行分类。

图2 显示，当气速低于0.83 cm/s 的最小流化速度时，床层流态处于固定床阶段，压降标准差基本保持在25 Pa 左右，波动幅度很小且稳定。当气速（区间为0.83～1.61 cm/s）超过最小流化速度时，压降标准差出现了一个小幅阶跃，保持在50 Pa 左右。在此区间内床层高度随着气速增大而增加，将其称之为膨胀区间，如图2 绿色区域。与固定床的基本稳定相比，膨胀区间内的压降标准差随气速有着一定程度波动，但并未随之增大而是维持在一个动态稳定范围，说明存在着某种因素稳定着床层波动。关于床层稳定性主导物理原因是颗粒间接触力或是流体动力学效应的争论由来已久，但可以确定的是，接触力贡献是在讨论气固两相流现象中难以回避的因素[19]。颗粒间接触力存在已经被具体试验证实，在稳定流化床膨胀的窗口中，存在与持续接触颗粒网络相关的屈服应力[20]，而颗粒间持续接触产生的屈服应力正是气固流化床进行稳定膨胀的最可能机制[21]。固定床中颗粒间互相紧密接触，稳定力起主导作用，因而保持基本稳定。当处于膨胀区间时，床层随气速升高而膨胀，床层浓度下降。由于颗粒间接触力与床层浓度呈正相关，接触力随气速降低。气流作用增强，稳定作用削弱，由此而来的不稳定性产生了不均匀的介观结构（气泡运动等），造成了一定程度的波动。然而，在膨胀区间内，稳定力虽然减小但并未完全消失。在其余留作用下，使得波动仍维持在一定范围内，而非随气速显著增加。当气速大于1.61 cm/s 时，压降标准差随气速增长出现了一个迅速拉升，波动幅度大于150 Pa。此时，流化床处于完全流化阶段，床层膨胀停止，空隙率的增大使得颗粒间的接触应力基本消失，对床层的稳定作用减小，气泡因此产生、生长、聚并、破裂，造成床内剧烈的波动。

偏度用来表征数据概率密度分布的不对称性，计算公式为：

当S= 0 时，数据概率密度分布关于均值对称，比如正态分布；当S＞ 0 时，概率密度分布右偏，数据出现右侧长尾，即众数小于平均数，数据的极端值在右边；当S＜ 0 时，概率密度分布为左偏，情况相反。

峰度F用来表征数据概率分布的陡峭程度，计算公式为：

当F= 0 时，峰值与正态分布相同；当F＞ 0 时，为高峰态，具有瘦尾，表示数据分布与正态分布相比较为尖锐；当F＜ 0 时，为低峰态，情况相反，且存在一个理论的峰度最小值为-2。

一般而言，将偏度和峰度相结合用来检验样本数据的分布是否满足正态分布。越接近正态分布，偏度和峰度越接近0。图3 和图4 显示了总床层压降的偏度和峰度随表观气速的变化。可以观察到，当流化床处于固定床与完全流化时，总床层压降的概率密度分布接近于正态分布。而当流化床处于膨胀区间时，偏度与峰度均呈现出显著大于0 的情况。此刻相较于正态分布，总床层压降概率密度右偏，且具有尖峰。说明床层固含率平均值右移，且有更大的概率出现极端值。因为颗粒间接触应力的存在使得颗粒分布具有维持接触的惯性，这才使得固含率的平均值偏大。极端值概率增大，并非是直观理解的气泡运动所造成的，而是因为在完全流化区间存在比膨胀区间更多的气泡，但其峰度仍回归于0。本文推测，这是颗粒间接触力的分布不均所造成的结果，局部颗粒间力的失效使得床层产生暂态空隙或气泡，更容易引起床层压降的突变。

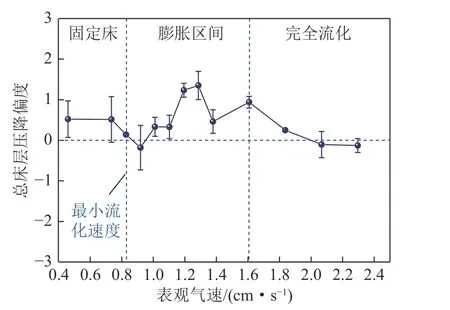
图3 总床层压降偏度随气速的变化Fig.3 Variation of skewness of total bed pressure with gas velocity

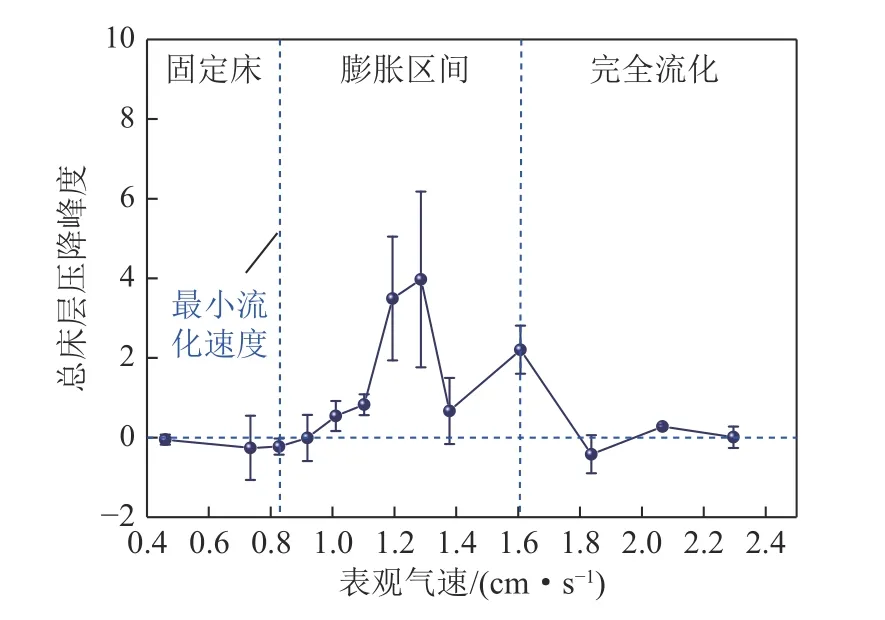
图4 总床层压降峰度随气速的变化Fig.4 Variation of kurtosis of total bed pressure with gas velocity

通过3 种时域分析表明，宏尺度分析只能在粗略范围上描述流化床的流动特征，但无法做到一对一映射。也就是说，同一个指标或许对应着不同的流动状态。若采用压降标准差进行表征，整个膨胀区间会被视为同等波动幅度的流动状态。而此时的偏度和峰度表明，在膨胀区间内，床层内部的流动状态随气速增长是具有显著变化的。这是因为床层波动的物理来源具有多尺度特性，复杂的介（微）观的波动耦合在一起，形成了近似的宏观波动。单纯的标准差分析难以区分膨胀区间的波动异同，而此区间处于调控干法重介质流化床分选密度的主要操作范围。因此需要将多尺度特征考虑进波动幅度的计算之中，从更介（微）观的尺度进行定量表征。

2.2 频域分析

频谱分析通常旨在获得时间序列中的主要频率，并将它们归属于各种物理现象。随着数字信号处理技术的高速发展，快速傅里叶变换及功率谱密度函数成为最常用的基本方法，在流化床的特征研究中发挥了重要作用[22]。通过功率谱密度函数提取出了风室中压力波动的3 个峰值频率，分别对应了气泡生成频率、气泡破碎频率和流化床的自然频率[23]。然而，傅里叶变换仅关注频率信息，对于频率随着时间变化的非平稳信号存在局限性。

压力波动通常是由床层振荡、气泡运动、和压力波传播等耦合作用产生的。研究中采集的压差信号反映的是测量间隔内的压力波动，等价于浓度波动。因此，影响因素主要为造成浓度变化的物理现象，如气泡行为、颗粒自激振荡等。而压力波的传播速度为10 m/s 量级，在10 cm 的传感器间隔中的差距忽略不计。研究中，需要着重关注的是对提取出的主要频率进行物理归因。虽然小波变换同时在时域和频域表示了信号，但也只能区分不同尺度的信号，而不能区分不同来源的压力信号。因此，采用功率谱密度函数提取主频并分析其产生的物理原因。

介尺度上，气泡引起的压力波动的特征频率通常为1～5 Hz。更具体地，不同剧烈程度的气泡所产生的特征频率也有所不同，见表2[24]。

表2 不同流化流态下的理想特征频率Table 2 Ideal characteristic frequency for different fluidization regimes

微尺度上，基于颗粒同相运动假设，浅层流化床中的颗粒受到重力和曳力的平衡束缚，在起始流化后存在自发的垂直简谐运动。该同相运动的假设只有在孔隙波能在半个周期内到达床顶时才成立，因此存在一个谐振最大床高，数量级约为几百个颗粒直径。对于深层流化床，振动不再是谐波，非简谐振动形成空隙。床越高，起泡模式越显著，自然振荡频率通常随着床层高度的增加而降低[25]。不少研究者从不同角度建立了深床的自然振荡频率理论方程，然而不少方程均低估了试验数据。将床层振荡类比于一端闭合另一端开放的风琴管，推导得出的方程如下，与试验数据较为吻合[26]。相关参数代入式（5）计算得到的理论流化床自然振荡频率见表3。

经过课程组2年多的案例库建设，案例库初步建成：独立编写了案例库框架；目前有具有装备特色的案例十七个，按照工艺特点分为铸造、锻造、焊接、机械加工四大类；收集大类工程材料、铸造、锻造、焊接、机械加工五大类动画、FLASH共有约1.5G。

表3 不同静床高下的理论自然振荡频率Table 3 Theoretical natural oscillation frequency of different static bed heights

式中：Hmf为临界流化时的床高；ρg为 空气密度；ρp为颗粒密度；φ为颗粒浓度；R为普适气体常量；T为绝对温度。

综合比较表2 和表3 所阐述的气泡特征频率和颗粒自然振荡频率，发现两者是比较接近的。流化床自然振荡频率的试验数据是通过将脉冲气流施加到在无气泡流化床上确定的。浅床作简谐运动而深床中的非简谐运动形成空隙，暗含了颗粒自然振荡与气泡频率的同源性。假设在临界最大床高时床层初始流化，理想情况下自然振荡频率与气泡频率相同。同时，考虑到上述提及的非鼓泡和鼓泡状态之间的非绝对性，气固流化床中存在小于气泡尺度的暂态空隙介观结构。如图5 红框所示，通过跟踪初始流化阶段的压力波动以确定暂态空隙的发展和湮灭。红框上的数字表示压力从谷值到右侧相对峰值的差值，这个差值是暂态空隙的快速经过所造成的，数字大小表征着暂态空隙的大小。红框连续跟踪了一个暂态空隙，它不像气泡一样随床高增长，而是在中间层达到最大值后衰减。因此，在实际情况中，推测床层颗粒振荡、暂态空隙、气泡之间存在一个演化关联。对比表2 和表3可知，当静床高小于40 cm 时，自然振荡频率与气泡频率在同一范围内，无法有效辨识。

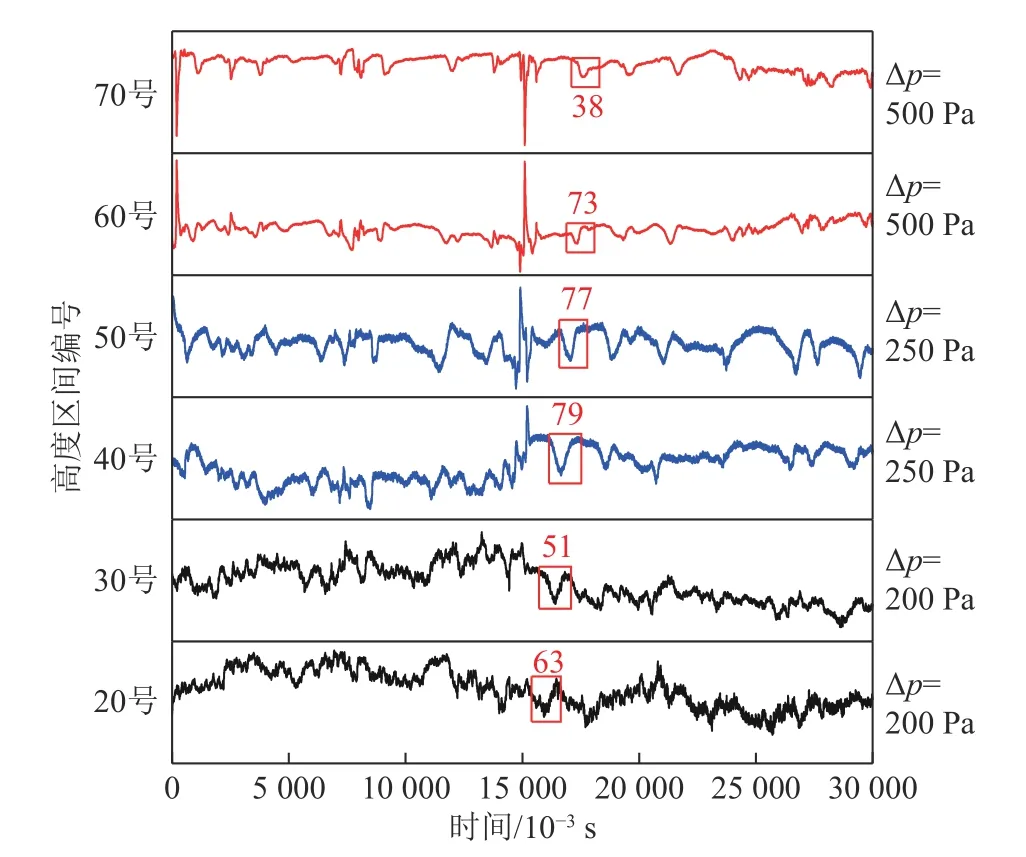
图5 初始流化时压差信号中的暂态空隙Fig.5 Short-lived void reflected in differential pressure signal during initial fluidization

因此，选取70 cm 静床高，测量不同床层位置的压差信号，以获得动态行为的完整描述，如图6 所示。

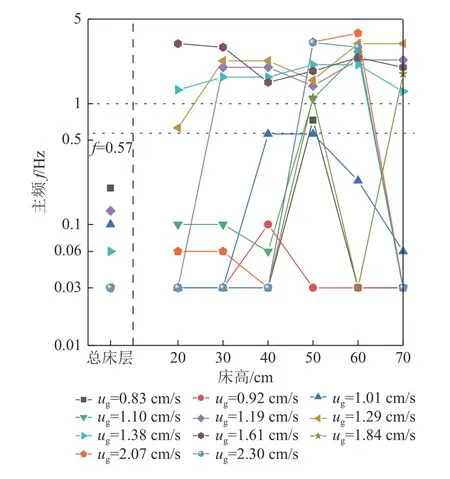
图6 床层压降主频随气速的变化Fig.6 Change of bed pressure drop frequency with gas velocity

图6 显示，各气速下的总床层压降主频均在0.2 Hz 以下，维持在一个相对稳定的波动范围。即便流化床进入完全流化状态，剧烈的鼓泡运动仅体现在局部波动频率，而对整体的影响不大。具体而言，除了在初始流化状态下，总床层主频偶尔为0.1～0.2 Hz之外，其余气速下的主频基本为0.03 Hz。对于局部的床层主频，大的波动始于床层中部。当0.83 cm/s ＜ug＜ 1.19 cm/s 时，流化床处于初始流化后的膨胀区间早期，40 号和50 号的床层主频从0.03 ～ 0.1 Hz跃升至到0.5 ～ 1 Hz，顶部与底部的床层主频大体不变。根据上文推测，床层自由振荡的频率为0.57 Hz，气泡的频率一般大于1 Hz，那么介于两者之间的暂态空隙频率应当在0.57 ～ 1 Hz。因此，在该阶段下的流化床主要受到暂态空隙的影响，与膨胀区间早期的实际情况相符合。当1.29 cm/s ＜ug＜ 1.61 cm/s时，流化床处于膨胀区间中末期，所有局部床层的主频都在1 Hz 以上，说明流化床在所有床高区间内均受到气泡控制。当1.84 cm/s ＜ug＜ 2.30 cm/s 时，流化床处于剧烈鼓泡下的完全流化状态，40 号和50 号的主频仍在1Hz 以上，而床层顶部和底部的主频回落到0.03 ～ 0.1 Hz。

值得令人关注的是，气泡主频仅在中末期的膨胀区间控制着整个流化床，而完全流化后的床层顶部与底部主频是相较稳定的，仅在中部受到气泡频率主导。气泡通常沿着床层向上发展演变，即在底部生成，在中部成长、聚并、破裂，在顶部喷发消散。据此，可以合理推测，床层局部的主频是基于事件的，与气泡的数量无关。在给定气速下，流化床底部的多分散小气泡与顶部的大气泡在相应位置所占据的气泡相体积比是稳定的。只有动态事件，如气泡生长、聚并和破裂，才会触发显著的浓度波动。

初始流化阶段存在的暂态空隙，受到接触应力的稳定作用，发展至床层中部达到最大值后衰减。气流在中层耗散，在此产生了0.5 ～ 1 Hz 的类气泡主频，而稳定作用下的床顶部和底部无此主频。当流化床处于膨胀中末期时，增大的气泡相驱动气流通过床层，使原本滞留在床层中部的气体逸出，且发展为继续增长的气泡。在2.1 节中描述了膨胀区间内床层偏离正态分布的不均匀情况，从侧面印证了颗粒间接触力的稳定作用抑制了床层流化，单泡作用是不均匀分布的结果。因此，在该状态下，整个床层的主频均大于1 Hz。而在完全流化的多泡状态，乳化相和气泡相在强烈的气体交换下维持着两相体积平衡，床的顶部和底部是均匀的，主频小于0.1 Hz。只有动态事件（气泡聚并、破裂）发生的中间层，导致床层浓度的剧烈波动，使得床层中部的主频大于1 Hz。

总结而言，压差信号分析在不同气速区间捕捉到的信号特征是不同，这对于今后探索空气重介质流化床如何精准密度调控提供了相应的科学指导。当流化床处于膨胀区间时，密度调控需要修正整个床层高度下气泡运动对分选密度的影响。而在完全流化的多泡区间，可以将关注重心集中在床层中部，重点研究动态事件造成的局部浓度波动对于分选密度的影响。同时，频域分析也体现出轴向差异传递，介尺度结构的发展在轴向高度区间存在不同的运动形式，能够依此作为定量评估多尺度结构对于床层浓度波动的影响幅值。

2.3 流化质量指数修正

从2.2 节可知，不同气速区间内的各轴向的主频存在不同的分布特征。即在膨胀区间内，全床层均受到气泡主频影响；而完全流化后，相对于床层上部和下部，气泡主频对床层中部的影响更大。虽然无法精准确定床层波动的物理来源，但可以知道介（微）尺度特征在轴向上的传递是具有差异性的。逆向思考，如果将轴向差异考虑进稳定性计算，等同于考虑了多尺度特征的影响。

因此，当描述流化床密度均匀稳定性时，不仅是简单地对总床层计算标准差，而是多段测量小跨度轴向区间内的波动，并将各轴向子区间内的主频作为此时床层标准差的权重值，得出了一个修正的流化质量指标，称之主频权重标准差，如式(6)：

式中：fi为轴向子区间内的压力波动主频；σi为轴向子区间内的压力波动标准差；n为划分的子区间数量。

将修正指数与原有的总床层标准差进行对比，如图7 所示。理论上如2.1 节分析，气速增高，稳定力削弱，气流作用增强，压降标准差表征的床层波动应随气速增加。但如图7 蓝色虚线框标识（比较了标准差上较为跳跃的点与修正后的情况），流化床的不均匀性会导致压降波动异常值，容易出现高于预期的波动，即气速低时的波动反而要比气速高时的波动大的多。这种异常的波动并非物理固有的，而是多尺度特征带来的系统性误差。图2 显示了通过多次试验取平均便能显著减少该误差的影响。若采用修正后的主频权重标准差，将2 种指标进行对比分析，可以直观地发现：修正指标下的波动异常值得到很好的抑制，随气速变化更具平滑性，且总体趋势与原有指标保持一致。可以得到结论，修正后的指标能够更具代表性地描述不同气速下的流化床的密度均匀性和稳定性，体现了多尺度特征对于床层波动的影响。

图7 流化质量指数修正与对比Fig.7 Correction and comparison of fluidization quality index

值得强调的是，流化质量指数表征的是床层稳定性，而并非分选意义上的指标。对于分选来说，稳定性只是调控的因素之一。固定床虽然稳定性高但不能达到所需的分选密度要求，单谈论稳定性是缺乏工程意义的。膨胀区间才是调控的主要操作范围。此时，分选密度基本达到要求，而床层稳定性高度影响着分选效率。然而在此调控区间内，复杂的物理因素使得精准评估床层稳定性是困难的。在此工程背景下，促使建立一种更精准的稳定性评估指标。

综上所述，标准差表征床层密度波动之所以不够精确，是因为仅提取了压力信号的时域特征，且在不均匀的多尺度特征的影响下，通常会表现出异常值，需要多次采样以消除系统误差。然而，要是精准地考虑不同物理现象所造成的波动及其波动幅度并进行叠加计算是困难的。同时考虑了时域和频域信息，并基于轴向差异传递特性，将多尺度问题简化为空间问题，定义出在多尺度分析下的流化质量表征指数。

3 结 论

1）Geldart A 类空气重介质流化床处于固定床与完全流化时，总床层压降的概率密度分布接近于正态分布。而当流化床处于膨胀区间时，由于颗粒间接触力的分布不均，局部处的颗粒间力失效使得床层产生暂态空隙或气泡，引起床层压降的突变，偏度与峰度均呈现出显著大于0 的情况，偏离正态分布。可知同一个标准差能够对应着不同的流动状态，通过标准差表征床层密度波动无法区分膨胀区间内的不同多尺度特征。

2）气泡主频在整体流化床中的体现存在于膨胀区间的中末期，而完全流化后的流化床仅在床层中部受到气泡频率主导。床层局部的主频是基于事件的，与气泡的数量无关。给定气速下的流化床内气泡相体积是相对稳定的，只有动态事件如气泡生长、聚并和破裂，才会触发显著的浓度波动。频率特征不仅体现在气速变化上，也在轴向传递上表现出差异性。

3）综合使用时频域分析方法，基于轴向差异传递特性，将多尺度问题简化为轴向空间差异从而引入流化质量指标。提出了以轴向主频为子区间标准差权重值的修正的流化质量指标。修正指标趋势与总床层标准差保持一致，并在此基础上有效地抑制了异常波动值，更具代表性地描述了干法重介质流化床的密度均匀性和稳定性。