响应变量随机删失时函数型非参数分位数回归模型的估计
2023-05-30杨锦涛凌能祥
杨锦涛, 凌能祥
(合肥工业大学 数学学院,安徽 合肥 230601)
0 引 言
近年来,随着收集和存储数据技术的进步,人们越来越多地收集到具有函数特征的诸如曲线、曲面、图像等数据,称之为函数型数据。函数型数据广泛存在于生物学、化学计量学、计量经济学、医学、气象学、神经科学等领域,如何进行函数型数据分析(functional data analysis,FDA)受到很多学者的关注。有关FDA的背景、建模理论和方法见文献[1-3]。
分位数回归是研究解释变量与响应变量之间关系的主要统计方法之一,自文献[4]的开创性工作以来,很多学者在此方向开展了研究。这种方法与传统的最小二乘回归相比,有许多优点,对于异常值的处理比均值回归更加稳健,因此有更好的估计效率。事实上,分位数回归模型已经应用于分析函数型数据。例如,在函数型线性分位数回归模型中,文献[5]利用光滑样条基重新表示函数型协变量,并给出估计量的收敛速度。同时,主成分逼近方法被广泛应用于研究函数型回归模型[6]。此外,非参数统计方法在函数型数据方面的研究进展见文献[7]。
在很多实际情况中,如抽样调查、生存分析、药物追踪测试和可靠性测试等,收集的数据可能是不完全的,如响应变量随机删失。最近,文献[8]提出函数型删失分位数模型,扩展经典截尾分位数回归中基于鞅的估计方法,以适应具有截尾响应和函数协变量的部分函数线性分位数回归模型,并给出估计量的渐近性质;文献[9]提出了响应变量删失时部分线性分位数回归模型。本文基于逆概率加权的方法,进一步研究响应变量删失时函数型非参数分位数回归模型的估计,并建立估计量的渐近正态性。
1 模型与方法
对于给定的分位数τ∈(0,1),考虑如下的随机删失响应函数型非参数分位数回归模型:
(1)

其中:ρτ(u)=u(τ-I)(u<0))为分位数损失函数;Kh=K(u/h)。
然而在删失响应变量的机制下,本文得到不完全的样本{(Xi,Yi,Δi),1≤i≤n},此处Xi被完全观测。本文提出mτ(χ)的逆概率加权分位数估计如下:

其中:Di=I{Y(i)≤y,Δ(i)=0};Δ(i)为对应于Y(i)的删失示性变量;Y(i)为{Y(i),i=1,2,…,n}的第i个次序统计量。
此外,本文提出的估计涉及到半度量,选取如下半度量[1]:
2 理论结果与假设
2.1 符号和假设条件
设B(χ,h)={y|d(y,x) 假设2 存在最大值L和常数c1>0,使得 假设3 存在c2>0和α>0,对于任意u,v∈F,有|mτ(u)-mτ(v)|≤c2d(u,v)α。 假设4 存在c3>0和c4>0,且φ(h)∈(0,∞),对任意χ∈F,有 0 假设5 当χ∈F时,存在1个确定的非负有界函数f1和趋向于0的非负的实函数φ,满足 (1)Fχ(t)=φ(t)f1(χ)+o(φ(t)),t→0; 假设1为核函数常见的假设[11];假设2为删失数据分析中常见的假设[7],确保对任意个体没有删失的概率都是正的;假设3~假设5为删失变量函数型数据分析中常见的假设[12];假设6为生存函数G(·)的常用的性质[11]。 定理1设假设1~假设6都成立,则有 其中 针对索拉非尼治疗失败的二线靶向药物的研究结果继续支持瑞戈非尼可作为肝功基础及体力状态评分较好晚期肝癌患者的二线靶向治疗药物。美国西奈山医学院Llovet等(摘要270)报告了两项使用雷莫芦单抗(RAM)的全球多中心3期临床研究,提示RAM作为HCC接受索拉非尼治疗后进展或不耐受的中晚期HCC且AFP≥400 ng/mL的二线治疗药物,mOS为8.1月,具有良好的安全性和显著的临床获益。瑞戈非尼作为二线治疗有效的药物,mOS为10月。该研究进一步支持了上述结论。 本节通过蒙特卡洛模拟研究文中所提估计方法的实际表现。考虑如下的模型[6]: (2) 表1 不同删失率下估计量的偏差和根均方误差 然后,设 引理1 设假设1~假设6都成立,则有 φ(h)(Mkf1(χ)+o(1)),k=1,2, 且 M1f(0|χ)+o(1)。 引理1的证明类似于文献[13]中引理1的证明。通过引理1和Lindeberg-Feller中心极限定理,得到如下引理2。 引理2 设假设1~假设6都成立,则有 N(0,σ2(χ)),n→∞。 其中 (3) 与文献[12]引理6的证明相似,有如下等式: (4) 根据文献[6],可以证明 (5) 由(4)式和(5)式可得: 其中,Wn是均值为0、方差为 的正态随机变量。根据文献[14]的理论结果,有 结合引理2,得到如下结论: 其中 本文基于随机删失逆概率加权的方法,提出响应变量随机删失时函数型非参数分位数回归模型的一种估计方法,并且给出估计量的渐近正态性,模拟实验验证了所提出方法的优越性和可行性。

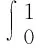

2.2 主要结果

3 模拟研究


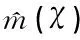
4 定理证明
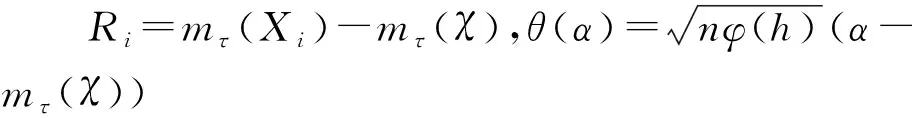
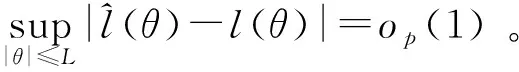
5 结 论
