碳纳米管填充聚合物复合材料电导率仿真研究

孙雪虎, 潘亭亭, 卢柏声, 刘彩霞, 鲁迎春

(1.合肥工业大学 微电子学院,安徽 合肥 230601; 2.合肥工业大学 物理学院,安徽 合肥 230601)

碳纳米管填充聚合物复合材料具有良好的力学性能[1]、电学性能[2]和热性能[3]等优势,在加固结构、加热元件、高电荷存储电容器、传感器等方面[4-5]被广泛使用。碳纳米管填充聚合物复合材料电学性能主要与电导率有关,其电导率依赖于多个参数,包括碳纳米管体积分数、长径比和空间分布等[6-8]。考虑诸多参数对电导率的影响,设计高性能的碳纳米管填充聚合物复合材料是一个具有挑战性的课题。仿真分析可在研究过程中灵活变换条件,实现填料在三维模型中的不同分布,为研究复合材料电学特性提供高效的低成本方法。文献[9]采用蒙特卡洛方法预测炭黑/碳纳米管混合填充复合材料的渗流阈值并分析填料尺寸变化的影响,但渗流阈值并不能完全反映聚合物的电学特性;文献[10]构建了填充直线型碳纳米管的复合材料模型,基于直线型填料假设研究碳纳米管长径比和电导率对复合材料电导率的影响,然而复合材料中碳纳米管多处于弯曲状态,形态变化会改变碳纳米管有效长度和复合材料中导电网络结构,从而影响复合材料电导率。

本文依据碳纳米管在复合材料中的实际形态,采用蒙特卡洛方法模拟弯曲碳纳米管在聚合物基体中的分布情况,构造碳纳米管填充聚合物复合材料三维模型,结合三维模型以及碳纳米管填充聚合物复合材料导电机理生成碳纳米管间电阻矩阵,应用大型纯电阻网络等效电阻计算方法求解电阻矩阵,得到复合材料电导率仿真结果。将仿真结果与实验数据进行对比,验证本文构建的电导率仿真模型的准确性,并研究碳纳米管长度和直径对复合材料电导率的影响。

1 复合材料电导率仿真模型

1.1 三维模型构建

碳纳米管填充聚合物复合材料被建模为三维代表体积单元(representative volume element,RVE), RVE是复合材料电导率仿真的最小单元,如图1a所示。RVE为正方体,表示分散着一定数量碳纳米管的聚合物复合材料。

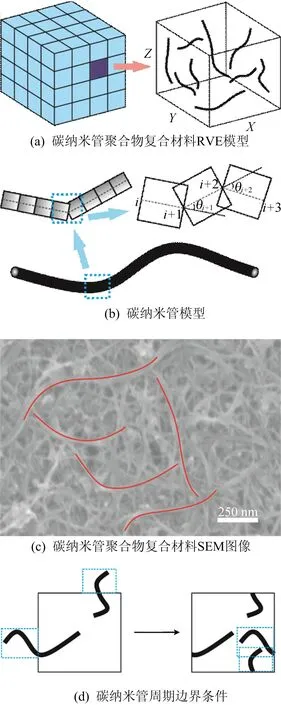
图1 碳纳米管聚合物复合材料RVE模型构建过程

考虑到复合材料中多数碳纳米管可弯曲,碳纳米管被建模为一系列通过连续节点相连的小线段,如图1b所示。根据碳纳米管物理性质,为了在不发生原子破坏的情况下,保持碳纳米管完美六边形结构[11-12],将2个连续小线段之间节点的旋转范围限制在120°以内。

本模型中,单根碳纳米管纤维长度L和直径D为实验中使用的碳纳米管平均长度和平均直径,构成碳纳米管纤维的每一根小线段长度与纤维直径相同。碳纳米管纤维在复合材料中分布的扫描电子显微镜(scanning electron microscope,SEM)图像如图1c所示,通过对比可知,本文建立的纤维模型与碳纳米管在复合材料中实际形态一致。

根据给定的碳纳米管体积分数,在RVE中随机放置足够数量的弯曲碳纳米管模型。考虑到管间短程范德华力相互作用,碳纳米管之间不能相互重叠。在RVE中创建一根弯曲碳纳米管纤维时,每根小线段根据其在碳纳米管中的位置顺序依次生成。第1根小线段被随机生成在未被其他碳纳米管占据的RVE空间中。若后续小线段与预先存在的碳纳米管不重叠,其生成位置与前一根小线段保持在同一直线上。若第i根小线段候选位置已存在其他碳纳米管,则在与第(i-1)根小线段相连节点旋转范围120°以内随机选择方向重新生成,避免碳纳米管彼此重叠。RVE中碳纳米管分布满足周期边界条件,即对碳纳米管超出RVE边界的部分,将其重定位放在RVE另一侧边界内,过程如图1d所示。

为研究不同碳纳米管体积分数下复合材料电导率变化,通常需要生成一系列RVE模型。模型中碳纳米管体积分数不同,碳纳米管长度、碳纳米管直径和RVE边长等参数保持不变。采用随机填料去除法可缩短这一系列RVE模型的生成时间,其过程分为如下2个步骤:① 给定碳纳米管长度、碳纳米管直径、RVE边长等参数,生成一个包含最大体积分数碳纳米管的RVE模型,将此模型称为主模型;② 为产生碳纳米管体积分数不同的RVE模型,根据所需体积分数在主模型中随机选择相应数量的碳纳米管,将其余碳纳米管从主模型中移除。

采用随机填料去除法生成不同碳纳米管体积分数RVE模型的过程如图2所示,图2中:主模型碳纳米管体积分数为10%;生成的RVE模型碳纳米管体积分数分别为1%、2%、5%。

1.2 电导率计算

碳纳米管填充聚合物复合材料导电机理的主要机制为量子隧穿,即电子通过隧道效应在碳纳米管间传输[13]。聚合物复合材料体系中碳纳米管间距离足够小时,即使纤维间没有直接物理连接,仍可通过量子隧穿实现导电。导通的碳纳米管间存在接触电阻Rcontact,计算公式[14-15]为:

(1)

其中:h为普朗克常数;e为电子电荷;M为填料-聚合物体系的导电通道总数;T为电子传输概率。

电子传输概率T与碳纳米管间距离有关,可通过求解具有矩形势垒的薛定谔方程[16]近似估计,其表达式为:

(2)

(3)

其中:d为2根碳纳米管之间的最短距离;D为碳管的直径;dtunnel为两碳纳米管之间的隧道距离;dvdw为范德华分离距离;dcutoff为隧穿截止距离;ћ为约化普朗克常数;me为电子质量;ΔE为聚合物与填料之间的功函数差。

根据泡利不相容原理,两碳纳米管之间的最短距离不小于范德华分离距离dvdw。(2)式中:当管间最短距离小于dvdw时,电子传输概率为定值,接触电阻与距离无关;当两碳纳米管间的最短距离在(dvdw,dcutoff)范围内时,接触电阻随距离增加而增大。若两碳纳米管间距离大于隧穿截止距离dcutoff,则应忽略隧道效应的影响,此时两碳纳米管看作未接触。根据(1)～(3)式计算碳纳米管间接触电阻,设dvdw为0.34 nm,dcutoff为1.4 nm,碳纳米管间电阻Rcontact与碳纳米管间距离d的关系曲线如图3所示。

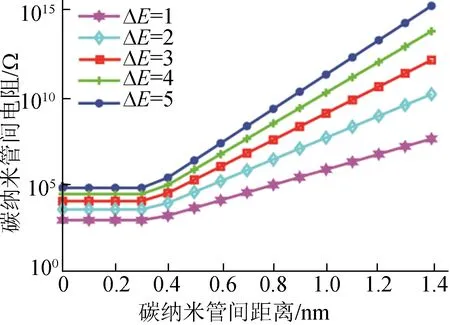
图3 碳纳米管间电阻与距离关系曲线

对于RVE模型中任意2根碳纳米管纤维,计算属于各自纤维的小线段之间距离,以此确定2条纤维之间的连通性。根据碳纳米管网络中每条纤维的连通情况识别跨越RVE的纤维渗流簇。每个簇从接触RVE左侧面的碳纳米管纤维开始,通过与这些纤维导通的其他纤维向右侧逐渐扩展。如果一个簇同时接触RVE左侧面和右侧面,那么这个簇将充当电流的传导路径,被称为一个渗流簇,如图4所示。

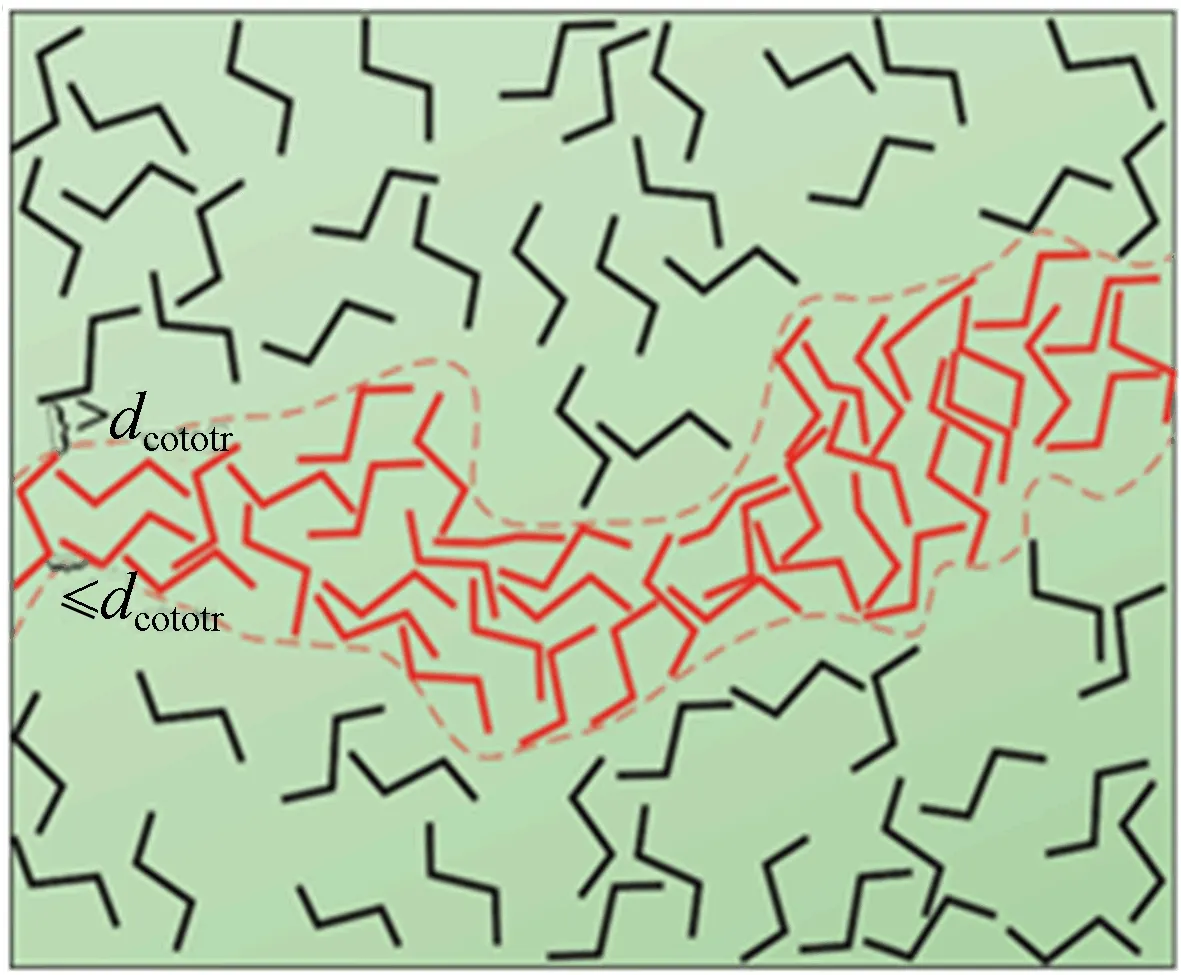
图4 碳纳米管聚合物复合材料中的渗流簇

图4中虚线范围内为渗流簇。属于非渗流簇的纤维不充当电流的传导路径,在计算RVE模型的等效电阻时被排除在外。

对于所有属于渗流簇的碳纳米管,构造碳纳米管间最短距离矩阵,即

(4)

利用碳纳米管间电阻(1)式计算所有碳纳米管纤维间电阻,根据最短距离矩阵生成碳纳米管间电阻矩阵,求解电阻矩阵得到复合材料总电阻。

根据无限电阻晶格结构中任意2个晶格点之间有效电阻计算的一般理论[17-18],将电阻矩阵代入大型纯电阻网络等效电阻计算公式,可得:

R=Gα α+Gβ β-Gα β-Gβ α

(5)

其中:R为RVE代表的碳纳米管填充聚合物复合材料总电阻;G为对电阻矩阵变换得到的求解结果;下标α、β分别代表RVE左侧面节点和右侧面节点。复合材料电导率σ的计算公式为:

σ=1/(Ra)

(6)

其中,a为RVE边长。

2 复合材料电导率计算模型验证

上述建模和计算过程构建了碳纳米管填充聚合物复合材料电导率仿真模型。选取合适的RVE边长,验证RVE各向同性并选取合适的电导率测量方向,对比仿真结果与实验数据,验证模型的准确性。依照多壁碳纳米管/环氧树脂复合材料实验数据[19-20],碳纳米管直径设为50 nm,长度为5 μm,聚合物基体电导率σ0设为10-6S/m,聚合物与填料之间的功函数差ΔE设为6 eV,导电通道总数M设为460,范德华分离距离dvdw设为0.34 nm, 隧穿截止距离dcutoff设为1.4 nm。

为选取合适的RVE边长,仿真中碳纳米管体积分数设为1%,研究碳纳米管填充聚合物复合材料电导率平均值与RVE边长的关系。随着RVE边长增大,实验重复20次复合材料电导率平均值变化如图5a所示。由于尺寸效应,RVE边长较小时电导率与边长成正比;随着RVE边长增大电导率趋于定值,在RVE边长与碳纳米管长度比值大于2.5时电导率基本不变,尺寸效应不影响复合材料电导率仿真结果。考虑到仿真结果准确性和仿真速度,碳纳米管长度5 μm时RVE边长设为12.5 μm。

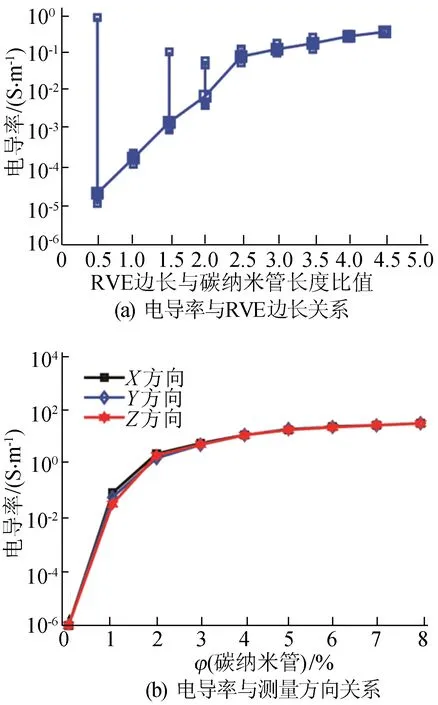
图5 碳纳米管聚合物复合材料电导率计算模型参数

为验证RVE各向同性,研究碳纳米管填充聚合物复合材料电导率与测量方向的关系。对于X、Y、Z3个测量方向,复合材料电导率与碳纳米管体积分数的关系如图5b所示,3个方向的电导率高度一致,表明复合材料电导率与方向无关。基于此,仿真中选择X方向作为电导率测量方向。

本文采用多壁碳纳米管/环氧树脂复合材料的电导率实验数据[21]作为对比,验证电导率仿真模型的准确性。碳纳米管填充聚合物复合材料电导率仿真结果如图6所示。由图6可知,碳纳米管体积分数较低时,复合材料中碳纳米管间距离大于隧穿截止距离,复合材料电导率接近聚合物基体电导率;随着碳纳米管体积分数增大,碳纳米管间距离减小导致接触电阻降低,复合材料内部形成导电网络,电导率急剧增大;碳纳米管体积分数达到一定水平时,复合材料内部导电网络密度变大,电导率趋于稳定。图6的仿真结果表明,本文构建的电导率仿真模型能够预测不同碳纳米管体积分数下电导率变化趋势,仿真结果与实验数据高度一致。

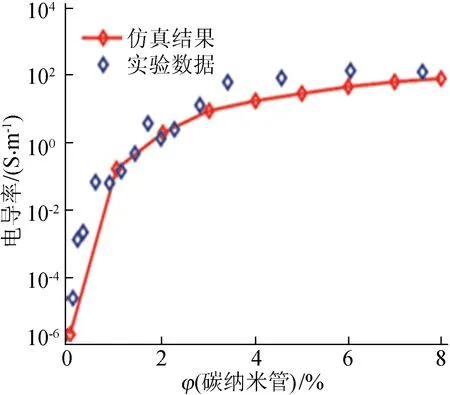
图6 碳纳米管聚合物复合材料仿真结果与实验数据对比

3 长度和直径对复合材料电导率影响

借助电导率仿真模型,研究碳纳米管长度和直径对碳纳米管填充聚合物复合材料电导率的影响,除碳纳米管长度和直径外,仿真中其他物理参数和几何参数与模型验证部分一致。

随着碳纳米管体积分数的增加,直径50 nm、不同长度碳纳米管的复合材料电导率变化如图7a所示。

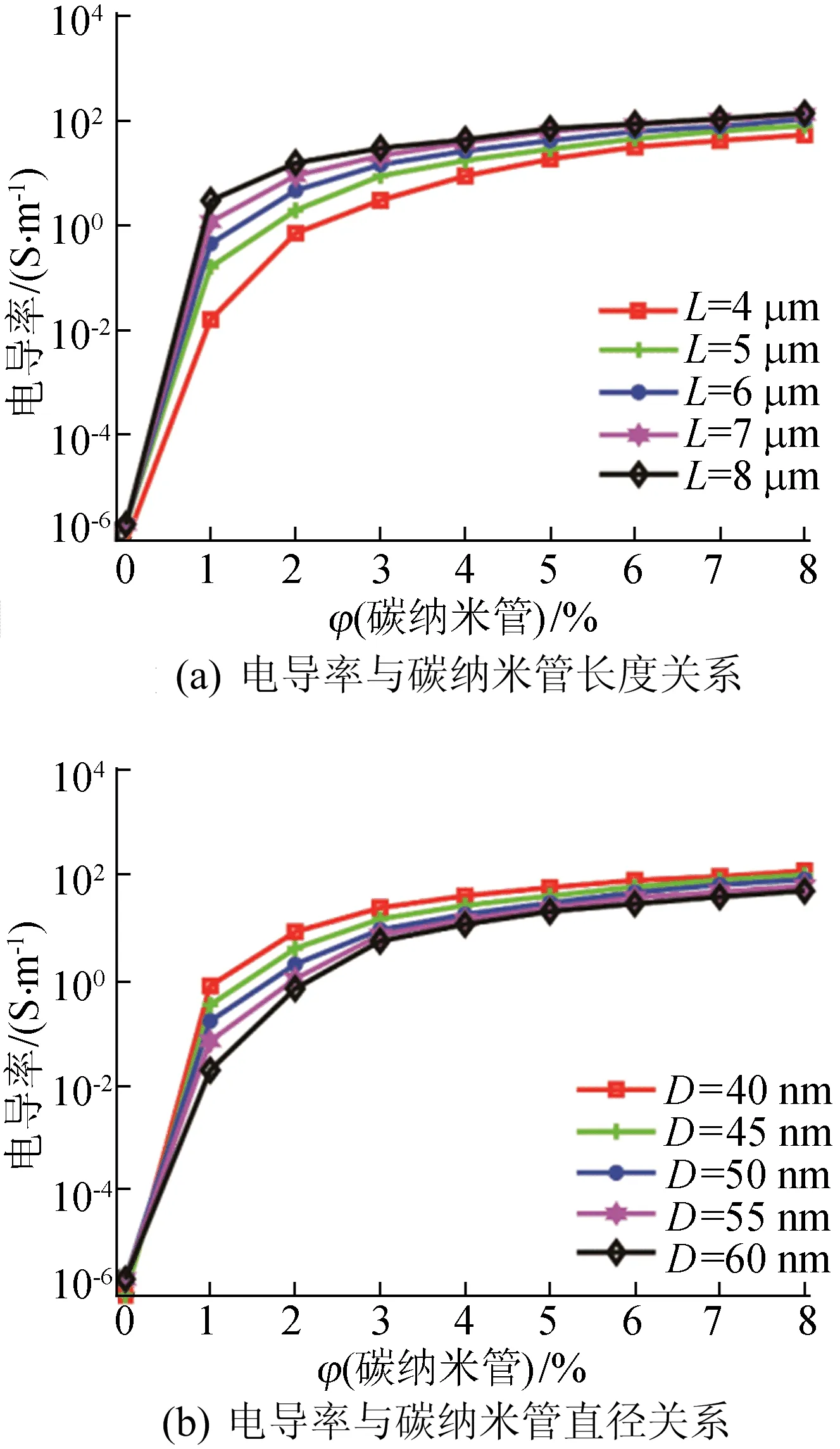
图7 长度和直径对碳纳米管聚合物复合材料电导率影响

由图7a可知,相同体积分数下,随着碳纳米管长度增加,复合材料渗流阈值减小,电导率增大。随着碳纳米管体积分数增加,长度5 μm,不同直径碳纳米管复合材料电导率变化如图7b所示。由图7b可知,相同体积分数下,随着碳纳米管直径增加,复合材料渗流阈值增大,电导率减小。综合图7a、图7b可知,随着碳纳米管长径比增大,碳纳米管间形成导电网络概率增加,复合材料电导率提高。碳纳米管长径比的增大有助于复合材料渗流阈值的减小,随着碳纳米管长径比增大,复合材料更快地从绝缘转变为导电。

4 结 论

本文构建碳纳米管填充聚合物复合材料电导率仿真模型,预测复合材料电导率,研究影响复合材料电导率的因素。仿真结果与实验数据对比表明,本文构建的电导率仿真模型可预测不同参数碳纳米管填充聚合物复合材料电导率。借助电导率仿真模型研究碳纳米管长度和直径对复合材料电导率的影响,相同体积分数下复合材料电导率随碳纳米管长径比增加而增大。本文建立的仿真模型可以为设计高性能的碳纳米管填充聚合物复合材料提供理论指导,同时为其他碳系复合材料电导率预测提供参考。