基于模型预测控制的四旋翼无人机双闭环控制

杨举 郑建立

摘 要：针对欠驱动非线性的四旋翼无人机轨迹跟踪问题，本文提出使用模型预测控制方法来解决小型四旋翼无人机的位置航向控制问题。在建立无人机动力学模型的基础上，采用双闭环路控制结构，对外环（位置控制环），MPC控制器旨在跟踪输入的参考轨迹；对内环（姿态控制环），为了实现对姿态的快速响应，将姿态子系统化为LPV表示，提出LPVMPC控制器使用二次规划求解。通过仿真验证了所提出的控制方法的有效性。

关键词：四旋翼无人机；模型预测控制；轨迹跟踪；线性变参数系统

现如今，四旋翼无人机无论是在军用还是在民用领域，四旋翼无人机都被广泛使用［12］。相比于大型无人机，四旋翼无人机价格低廉、操作简单、便于维修。四旋翼无人机系统具有六个姿态状态、四个电机，为典型的欠驱动、非线性、强耦合的系统［3］。

四旋翼无人机的飞行控制一直是无人机研究的重点［4］，内蒙古科技大学的江杰［5］使用准LPV法对四旋翼无人机系统建立了线性空间方程，设计了PID控制器；南京航空航天大学的周杰［6］设计线性扩张状态观测器对四旋翼外部阵风干扰进行估计，基于四旋翼无人机模型信息建立了模型预测控制器，实验结果表明算法有效且满足实际工程需要；武汉科技大学的程欢在他的硕士论文中，提出了外环模型预测控制（MPC）方法以实现位置跟踪，内环（姿态环）采用PID控制器以实现姿态跟踪，达到良好的控制效果［7］；武汉科技大学的杨艳华［8］扩展状态卡尔曼滤波估计了风力扰动，通过反馈将姿态动力学模型线性化，设计了ESKFMPC控制器；华东交通大学的许雪松［9］针对四旋翼无人机带负载时，负载重量、转动惯量不确定性的问题，提出了自适应载荷补偿的模糊自抗扰控制系统；华侨大学的林哲［10］在内环姿态外环位置控制中，利用模糊扩张状态观测器，对外部总扰动在线估计后设计非奇异快速终端滑模控制器，得到较好的控制效果。

本文提出了一种基于模型预测控制的双闭环轨迹跟踪控制方法。首先，建立一个四旋翼无人机的动态模型，在外环设计了基于MPC控制器对四旋翼位置的控制；其次对四旋翼无人机模型按准IPV方法变换，设计了基于MPClPV的姿态控制内环。最后，在MATLAB中进行仿真，位置和姿态轨迹跟踪控制的仿真结果证明了所提方法的有效性。

1 四旋翼无人机动力学数学模型

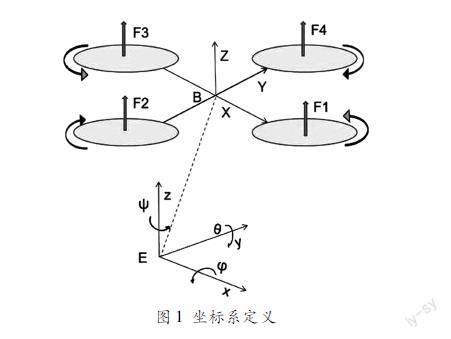
本文假设飞行器为刚体且质量为常数，飞行器几何外形对称，且内部质量对称。并且地面坐标系为惯性坐标系，重力加速度不随飞行高度而变化。定义四旋翼无人机的欧拉角θ φ ψ，其中θ定义为俯仰角，角度范围为-π2<θ<π2；φ定义为横滚角，角度范围-π2<φ<π2；ψ定义为偏航角，角度范围为-π2<ψ<π2。

根据四旋翼无人机的机理原理，可由牛顿欧拉方程得到：

mζ¨=F

Iη=-η×Iη+τ（1）

式（1）中，m为四旋翼无人机的质量，ξ=xyzT为四旋翼无人机在大地坐标系的位置，F为四旋翼无人机所受合力；I=diagIxIyIz代表惯性张量对角矩阵，η=pqrT代表四旋翼无人机的机体角速度，τ为四旋翼无人机所受合力矩。

四旋翼无人机旋翼产生的总升力Uf1为：

Uf1=F1+F2+F3+F4（2）

其中Fi代表四旋翼无人机所受第i个旋翼所产生向上的力，大小与转速的平方成正比。为了便于控制，飞行的状态被分为四个：上下，左右，前后，偏航。上下控制变量为U1，当U1大于机体重力时，四旋翼无人机向上运动，反之则向下。与上下飞行状态类似，其他三个变量定义如下：

U2=lF4-F2=λlω24-ω22

U3=lF3-F1=λlω23-ω21

U4=μω24-ω23+ω22-ω21（3）

式（3）中λ为升力系数，μ为扭力系数，l为无人机质心到旋翼中心的距离，ω2i为第i旋翼转速的平方值。

四旋翼无人机在飞行中产生的陀螺力矩表达式为：

τg=Ipη×0 0 ωTT（4）

其中，Ip为四旋翼无人机的转动惯量，ωT为旋翼的相对转速。ωT可写为：

ωT=ω4-ω3+ω2-ω1（5）

最终可以得到四旋翼无人機的合外力矩，整体表达式如下：

F=REB∑4i=1FTi-m00gT

τ=-τg+τT（6）

忽略四旋翼无人机机体和旋翼的陀螺效应，可得四旋翼无人机的一般动力学模型如下［11］：

x¨=cosψsinθcosφ+sinψsinφU1m

y¨=sinψsinθcosφ-cosψsinφU1m

z¨=cosθcosφU1m-g

φ¨=Iy-IzIxψθ-IpIxθωT+U2Ix

θ¨=Iz-IxIyψφ+IpIyφωT+U3Iy

θ¨=Ix-IyIzθφ+U4Iz（7）

2 四旋翼无人机控制器设计

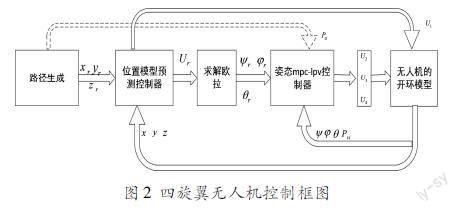
本文采用双环模型预测控制方案来进行四旋翼无人机的轨迹跟踪控制，其中，内环为姿态控制器，外环为位置控制器。首先根据参考轨迹和位置控制器求出U1，将U1代入求解出另外两个位置控制变量uxr和uyr；然后逆向求解欧拉角得到三个参考角ψr、φr、θr。再由姿态控制器求出U2、U3、U4；最后将U1、U2、U3、U4代入四旋翼无人机模型中，将四旋翼实际位置、姿态状态变量，反馈到各自的控制器，从而形成双闭环控制系统。

2.1 外环位置控制器设计

在此我们假设四旋翼无人机模型是一种线性定常离散时间的状态空间模型，虚拟参考状态空间模型在没有外部干扰，并且四旋翼无人机高度稳定的情况下，得出：

U1r=m·z¨r+g，uxr=x¨r·mU1r，uyr=y¨r·mU1r（8）

fξk+1=A-k·fξk+B-k·u～ξ（k）（9）

式（9）中矩阵A-k表示与fξk相关的雅克比式矩阵，矩阵B-k表示与uξk相关的雅克比式矩阵，将其分为高度误差模型和x，y误差模型。

四旋翼无人机高度误差模型为：

fξzk+1=Azk·fξzk+Bzk·u～ξz（k）（10）

式（10）中，Az=1Δt

01，Bz=0

Δtmcosθkcosφk，Δt为采样时间。

针对高度位置控制，控制输入U1将通过下列的二次规划问题求得［7］：

minJz=［f^ξz-f^ξrz］TQz［f^ξz-f^ξrz］+［u～^ξz-u～^ξz］TRz［u～^ξz-u～^ξz］

stf^ξz-Pk|kf^ξzk|k-Hzk|ku～^ξz=0

u～^ξzi

公式（11）中Qz和Rz是定义的对角加权矩阵。因此，U1k可通过下式求得：

U1k=u～^ξzk|k+U1rk（12）

X、Y轴的控制将高度Z轴控制的U1当作已知量，进而转化为分别求和ux和uy的变量函数。四旋翼无人机x，y方向的位置误差模型采用如下式：

fξxyk+1=Axyk·fξxyk+Bxyk·u～ξxy（k）（13）

由式（13）得到x，y方向的移动误差模型对应的矩阵Axy和Bxy分别为：

Axy=1Δt00

0100

001Δt

0001和Bxy=00

ΔtmU1k0

00

0ΔtmU1k（14）

式（14）中Δt是采樣时间。针对下x，y方向的位置控制输入，参照高度位置控制方式可以简单得出。

2.2 内环位置控制器设计

四旋翼无人机姿态控制内环采用LPVMPC控制器。从位置控制器中接收的参考值θrφrψr与无人机开环模型反馈的实际值θφψ，通过LPVMPC姿态控制器计算，得到U2U3U4。在应用MPC控制策略之前，有必要将无人机的非线性模型转换为LPV格式。由于MPC控制器仅处理上述三个角度，因此将重新排列为LPV格式。如果四旋翼无人机稳定在接近悬停位置，则φ和θ角可视为零角度。

该方程组现在将用于MPC控制器设计。值得注意的是，姿态控制的内环四倍比位置—速度控制外环更快。在MPC策略中，使用的预测范围为5个样本，姿态MPC成本函数公式的二次规划问题与高度控制相似［12］。

3 仿真结果

四旋翼无人机飞行参考轨迹的跟踪仿真结果如图3、图4和图5所示。图3是一个三维轨迹跟踪；图4分别显示了x、y和z方向的路径跟踪；图5分别显示了姿态角度的良好跟踪。如图3、图4和图5所示，四旋翼无人机通过使用MPC双闭环控制方法可以在飞行中实现良好的路径跟踪。图6、图7、图8展示了不同轨迹下的四旋翼无人机飞行参考轨迹的跟踪仿真结果，图6是一个三维轨迹跟踪；图7分别显示了x、y和z方向的路径跟踪；图8分别显示了姿态角度的良好跟踪。

结语

基于以上分析，级联式双闭环模型预测控制可以实现四旋翼无人机飞行中的路径跟踪，取得非常好的效果，无人机的六个自由度都以非常小的误差进行跟踪。本文提出将模型预测双闭环控制方法用于四旋翼无人机轨迹规划的控制，将姿态控制视为独立的问题，使用模型预测双闭环控制结构。对内环姿态控制，使用将lPV系统的MPC控制问题转化为QP优化问题，从使用成熟的数值算法在线求解；对外环位置控制，使用MPC算法使实际位置轨迹对参考轨迹实现良好跟踪。通过仿真实验验证了本方法的合理性。

参考文献：

［1］丁承君，尹李亮，段萍.应用于植保无人机的定位数据修正方法设计［J］.传感器与微系统，2018，37（7）：9295.

［2］Gupte S，Mohandas P I T，Conrad J M.A survey of quadrotor unmanned aerial vehicles［C］.Proceedings of Southeastcon.IEEE，2012：16.

［3］Zulu A，John S.A review of control algorithms for autonomous quadrotors［J］.Open Journal of Applied Sciences，2014，04（14）：547556.

［4］Xu M，Zhang R，Chen L，et al.Key technology analysis and research progress of UAV intelligent plant protection［J］.Smart Agriculture，2019，1（2）：2033.

［5］江杰，岂伟楠.四旋翼飞行器建模与PID控制器设计［J］.电子设计工程，2013，21（23）：147150.

［6］周杰，王彪，唐超颖.基于状态空间模型预测算法的四旋翼无人机飞行控制［J］.信息与控制，2018，47（2）：149155.

［7］程欢.基于模型预测控制的四旋翼无人机路径跟踪控制研究［D］.武汉科技大学，2018，5.

［8］杨艳华，吕童，柴利.基于ESKFMPC的四旋翼无人机轨迹跟踪控制［J/OL］.电子测量与仪器学报：18［20220830］.http：//kns.cnki.net/kcms/detail/11.2488.TN.20220610.1736.008.html.

［9］徐雪松，吳仪政，倪赟.变载荷四旋翼无人机的自适应模糊自抗扰控制［J］.传感器与微系统，2022，41（07）：101105+109.

［10］林哲，李平.采用模糊扩张状态观测器的四旋翼无人机滑模轨迹跟踪控制［J/OL］.华侨大学学报（自然科学版）：19［20220830］.http：//kns.cnki.net/kcms/detail/35.1079.N.20220629.1156.002.html.

［11］彭川.基于高斯过程模型预测控制的四旋翼无人机轨迹跟踪控制［D］.武汉科技大学，2021，5.

［12］Mark Schmidt.Deriving the Gradient and Hessian of Linear and Quadratic Functions in Matrix Notation.February 6，2019.

［13］MATLAB，“Quadraticprograming @ONLINE，”［Online］.Available：https：//es.mathworks.com/help/optim/ug/quadprog.html？lang=en.

作者简介：杨举（1997— ），男，汉族，河北邯郸人，研究生在读，研究方向：四旋翼无人机先进控制方法、逆变器的先进控制方法。