考虑需求关联性的多供应商电商库存分配研究

李昀洲 陈璐

摘要：需求关联性现象普遍存在于顾客购买行为中，然而大多数库存管理方面的研究假设产品需求相互独立，忽视关联性造成的影响，可能导致严重的缺货现象发生。针对存在需求关联性情况下具有库存容量限制的多供应商电商库存分配问题，应用FP-Growth算法从订单数据库中挖掘得到关联规则，并将关联规则抽象为一种约束，建立双目标随机规划数学模型，通过分段线性拟合方法对非线性目标函数和约束进行处理。采用非支配排序遗传算法（NSGA-Ⅱ）对模型进行求解，基于“先知种群”改进种群初始化过程，以提升算法收敛速度。使用真实数据的数值实验表明，基于关联规则的库存分配模型能以小幅度增加运营成本为代价，显著减少缺货数量。最后对库存容量、关联规则置信度和供应商个数进行敏感性分析，进一步为电商平台管理者提供了参考。

关键词：库存分配；需求关联性；关联规则挖掘；多供应商；多目标优化；库存容量约束

中图分类号：F 272.3

文献标志码：A

随着我国线上交易市场的急剧扩大，电商平台之间的竞争也愈发激烈。库存分配作为电商供应链管理中的重要问题，代表着电商平台的核心竞争力[1]。电商供应链体系包含成千上万种不同产品，在大多数情况下，产品之间的需求量存在关联性，比如顾客购买手机时，会倾向于同时购买耳机、手机壳等附属产品[2]。由于对未来需求的预测必然存在误差，如果忽视不同产品之间的关联性，可能会导致严重的缺货现象。例如，某些事件引起手机的需求量大幅上升，且电商平台准确预测到了这一趋势，并及时增加手机的订货量，但由于忽视了产品之间的关联性，平台并未增加耳机、手机壳等产品的订货量，从而导致其大量缺货的现象发生。可以看出，在库存分配策略中考虑需求关联性的影响，将有助于减少缺货现象的发生。此外，电商平台往往采用多供应商或多运输方式（例如空运和陆运）的订货模式，以应对不同的单位运输成本和运输提前期[3]。管理者需要综合考虑增加成本与减少缺货量之间的平衡关系，在多个供应商和运输方式中进行选择，并确定最优的订货量[4]。

然而，过往有关需求关联性对于库存管理影响的文献，大多集中在研究无库存容量限制、单供应商、联合补货模式中某种既定库存控制策略的最优参数设置问题。Song[5]研究了需求存在关联性条件下的base-stock库存控制策略，使用多元复合泊松分布定义关联性需求。Liu等[6]考虑两种相互关联产品的联合补货问题，采取can-order库存控制策略，通過建立马尔可夫模型得出预期总成本的表达式。Feng等[2]采用与Song相似的需求模型，针对多产品联合补货问题，在can-order库存策略的基础上提出（s，c，d，S）库存策略。Zhang等[7]针对绑定销售的两产品问题，推导出最优的EOQ策略参数表达式。Poormoaied等[8]考虑（Q，r）策略下两种互补产品的库存控制问题，使用基于仿真的方法得到最优的策略参数。这些研究均基于现有的库存控制策略，但本文研究的有库存容量限制的多供应商库存分配问题，已被证明难以找到一种最优的库存控制策略[9-10]，因而以上方法并不适用。

针对以上问题，本文考虑具有库存容量限制的电商多供应商库存分配问题，研究需求存在关联性情况下的最优库存分配策略。产品的关联性常通过关联规则的方式体现，常用的关联规则挖掘算法包括Apriori算法、FP-Growth算法等，其中FP-Growth算法因其挖掘效率较高而被广泛使用[11]。例如，Lin[12]针对多供应商供应链系统，使用FP-Growth算法对供应商进行分类。梁泉等[13]应用FP-Growth算法挖掘公共交通出行数据中的关联规则，对不同类型的通勤人群进行划分和识别。因此，本文采用FP-Growth算法实现库存分配问题中产品需求的关联规则挖掘，以减少可能出现的严重缺货现象。

在过往库存管理研究中，大多将缺货成本纳入总成本中进行考虑[3]，然而在现实场景中缺货成本难以准确衡量[14]，这使得缺货成本的计算与实际存在一定差距，针对该问题，现有研究往往使用最小化缺货数作为优化目标[15]。因此，本文构建以最小化预期缺货数和最小化总运营成本为目标的双目标随机规划模型。供应链和库存管理方面的多目标优化研究，大多将不同类型的成本以及其他外部因素作为优化目标。任宏涛等[16]研究资源约束下的绿色铝供应链网络，建立多目标模型，目标函数为最小化经济成本和水资源消耗。Lagos等[17]研究一种多目标选址库存问题，针对选址成本和库存成本进行建模优化。姜芳等[18]针对塑料制品回收利用物理网络，构建了以最小总成本、最低碳交易成本、最小环境影响程度为目标的多目标优化模型。张天瑞等[19]考虑可持续闭环供应链网络中的多目标优化问题，目标函数为最小化运营成本和环境伤害，以及最大化社会效益。

基于上述问题，本文针对有库存容量限制的多供应商电商库存分配问题，建立以最小化预期缺货数和最小化总运营成本为目标的随机规划模型，通过分段线性拟合方法对非线性目标函数和约束进行处理。随后，使用FP-Growth算法挖掘得到关联规则，将其形式化为一种约束以提升模型表达能力，并使用基于“先知种群”的种群初始化方法改进NSGA-Ⅱ算法以提升其收敛速度。最后，通过使用真实数据的数值实验对模型方法进行验证和分析。

1 关联规则挖掘

1.1 关联规则定义

根据 Agrawal 等[20] 的定义，假设为产品集合，给定交易数据集 ，

其中每个订单（ transaction） t 是 I 的非空子集，即。关联规则（association？rule）是形如 的表达式，满足 且 ，其中，X 被称为前项产品（antecedent？products），Y 被称为后项产品（consequent？products）。任意产品集 在 D 中出现的频繁程度用支持度（support）来进行衡量，其定义为

1.2关联规则挖掘

本文使用的数据集来源于国内最大的电商平台之一，包含超过550万条订单数据，覆盖各个品类约1 500种产品。为了研究的简明性，从中选取销量靠前的100种产品进行关联规则的挖掘，原因如下：a．选取的100种产品的销量之和占总销量的70%以上；b．选取的产品涵盖各个品类，多样性较强；c．選取的产品销量较为稳定，受季节性影响不大。

本文使用FP-Growth算法进行关联规则挖掘，挖掘过程中需要对数据集进行两遍扫描。第一遍扫描时统计各元素出现的频率，丢弃非频繁的元素，并根据出现频率进行排序；第二遍扫描时构建FP-tree数据结构，并根据最终获得的FP-tree挖掘频繁项集，进而得到关联规则。设置最小支持度为200，最小置信度为0.8，对真实数据集中的5 500751条订单数据进行挖掘，得到16条关联规则约束，部分结果如表l所示，其中包含每条规则的前项产品、后项产品，以及规则的置信度。

2 模型构建

本文研究一个多供应商的库存分配问题，考虑三级电商供应链网络，由多个供应商和多个前置仓组成，需要对供应商与前置仓之间的库存分配进行最优决策，在尽可能减少缺货数的同时降低总运营成本。当前置仓出现缺货现象时，电商平台将会失去未被满足的需求。本文考虑多个时间周期维度，在每个周期开始时，前置仓管理者需要选择供应商和确定订货量进行订货，并在对应的lead time之后收到货物。前置仓运营成本包括运输成本和存储成本。本文基于以下假设：a．各供应商至前置仓的单位运输成本和运输提前期已知，且不随时间变化；b．前置仓内各产品的单位存储成本和前置仓的库存容量上限已知，且不随时间变化；c．各供应商相同产品的进价相同；d．产品的售价保持不变；e．产品在存储过程中不存在腐败、折旧等问题；f各产品需求服从正态分布；g．各产品毛利率相近。

2.1 符号说明

2.2 基于关联规则的电商库存分配模型

建立基于关联规则的电商库存分配双目标随机规划模型：其中，目标函数（1）为最小化总缺货量，在前文中假设各产品利润率相近，因此，使用总缺货量来衡量缺货造成的损失。目标函数（2）为最小化总运营成本，包括运输成本和存储成本。约束（3）是多个周期的库存更新约束；约束（4）计算了每种产品在每个周期内的平均库存水平；约束（5）是供应商供应量约束；约束（6）确保每个前置仓的总库存量不能超过其库存容量上限；约束（7）为需求关联性约束，保证后项产品在获得补货后的库存水平不低于前项产品库存水平乘以关联规则置信度；约束（8）确保缺货量不能超过需求量；约束（9）和（10）规定了所有变量的取值范围。

由于随机变量 的影响，该随机性模型无法直接进行求解，需要将随机变量进行转化。首先对目标函数（1）中的缺货数进行处理，记周期t时在前置仓k中产品i获得补货后的库存水平为Titk，其表达式为

将式（11）代人目标函数（1）中，并将约束（3）替换为式（12），即可得到转化后的确定性模型。

2.3模型线性化处理

在上文得到的确定性模型中，包含非线性目标函数（1）以及非线性约束（12），为了提升模型的求解效率，需要对其进行线性化处理。目标函数（1）的形式满足正态函数一阶损失函数，其一般性形式为 根据Rossi等[21]提出的方法，可将标准正态分布一阶损失函数进行分段线性化拟合，经过综合考虑拟合效果和复杂度，本文选择使用五段函数进行线性拟合。通过转化，可得到正态分布一阶损失函数L（x，ω）的分段线性拟合表达式为

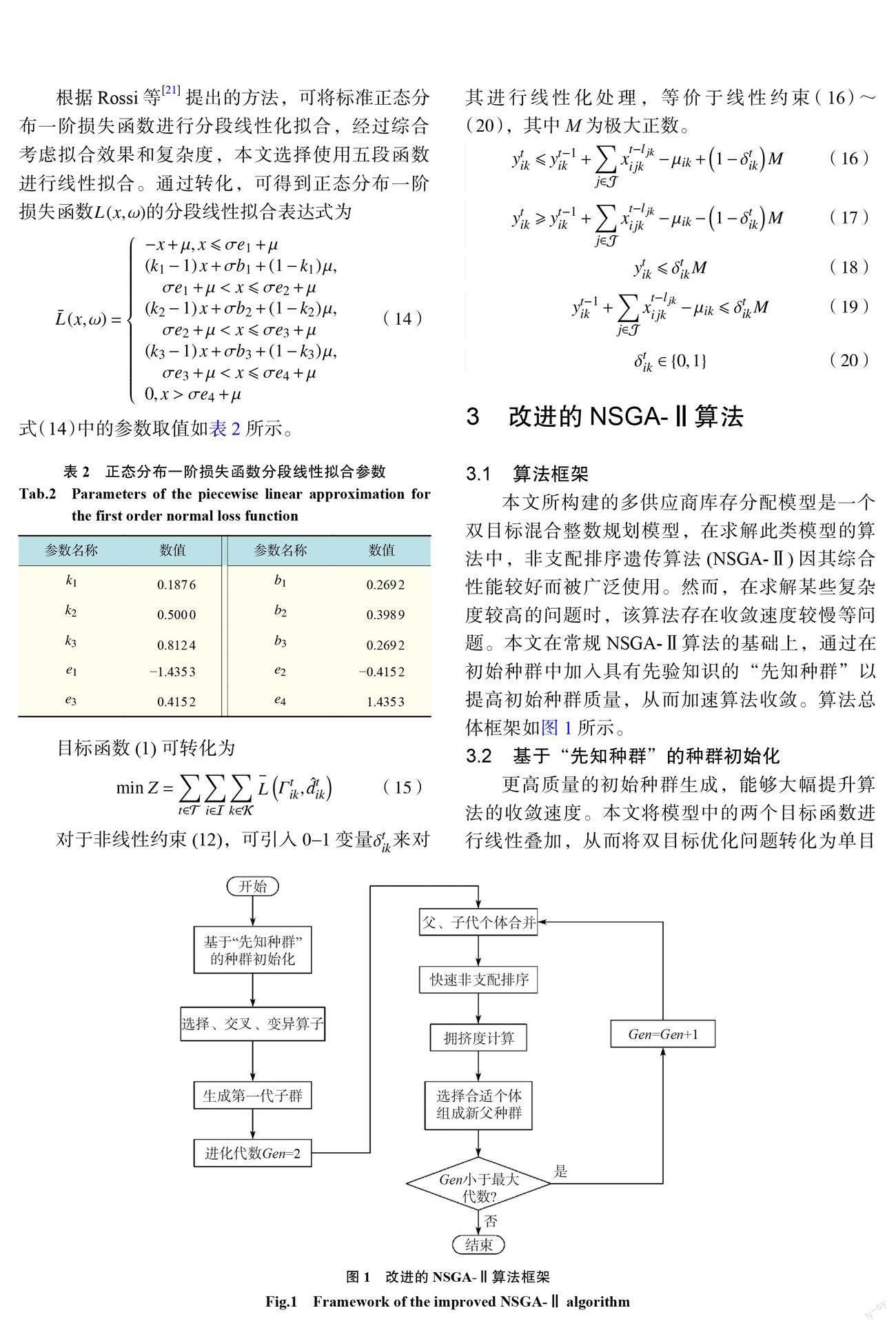
3 改进的NSGA-Ⅱ算法

3.1 算法框架

本文所构建的多供应商库存分配模型是一个双目标混合整数规划模型，在求解此类模型的算法中，非支配排序遗传算法（NSGA-Ⅱ）因其综合性能较好而被广泛使用。然而，在求解某些复杂度较高的问题时，该算法存在收敛速度较慢等问题。本文在常规NSGA-Ⅱ算法的基础上，通过在初始种群中加入具有先验知识的“先知种群”以提高初始种群质量，从而加速算法收敛。算法总体框架如图1所示。

3.2 基于“先知种群”的种群初始化

更高质量的初始种群生成，能够大幅提升算法的收敛速度。本文将模型中的两个目标函数进行线性叠加，从而将双目标优化问题转化为单目标优化问题。同时，使用Gurobi求解器进行求解，将得到的高质量解称为“先知种群”，即带有先验知识的种群，并加入到随机生成的初始种群中。由于两个目标函数的数量级不同，在进行线性叠加前需要进行归一化处理，步骤如下：

a．将目标函数设置为最小化总缺货数量Z，使用Gurobi求解器进行求解，得到的总缺货数记为Zmin，总运营成本记为Cmax。

b．将目标函数设置为最小化总运营成本C，使用Gurobi求解器进行求解，得到的总运营成本记为Cmin，总缺货数记为Zmax。

c．设置新的目标函数为式中，α，β为对应的权重系数，且满足α+β=1。

d．通过设置多组不同的权重系数值，得到多组单目标函数，并使用Gurobi求解，得到的解即为“先知种群”，将其加入到随机生成的初始种群中。

3.3 算法改进效果验证

为了验证算法改进后的效果，设置一组包含10种产品，2个供应商和4个前置仓的小规模算例，分别使用常规NSGA-Ⅱ和改进后的NSGA-Ⅱ算法进行求解，并使用种群平均预期缺货数Zavg与平均总运营成本Cavg的调和平均值Q= 作为衡量收敛性的指标，结果如图2所示。可以看出，改进的NSGA-Ⅱ算法在迭代10次左右即达到收敛，而常规的NSGA-Ⅱ算法需要迭代60次左右才能收敛。由此证明，改进的NSGA-Ⅱ算法可以大幅加快收敛速度，提升求解效率。

4 数值实验

通过数值实验对模型和算法进行验证分析，将电商平台真实数据集拆分为60%的训练集和40%的测试集。使用训练集进行关联规则挖掘和需求拟合，并使用上文提出的模型和改进的NSGA-Ⅱ算法进行求解，得到最优订货量。最后使用测试集进行验证，计算真实产生的总运营成本和缺货数。根据实际场景，考虑100种产品，2个供应商，3个前置仓，时间周期数为4。

4.1 需求關联性的影响分析

为了分析需求关联性带来的影响，分别使用考虑关联性的模型和不考虑关联性的模型（去除需求关联性约束）进行求解，将得到的解集用测试集数据进行验证，并计算得出每个解实际产生的缺货数和总运营成本，如图3所示。同时选取考虑关联性和不考虑关联性结果中总运营成本最小的结果，并将其对应的缺货数进行对比，如表3所示。可以看出：考虑需求关联性的情况下，总运营成本会因为订货量的增加而随之上升，同时产生的缺货数会大幅下降；对于总运营成本最低的结果，考虑关联性的情况下，总运营成本仅上升2.3%，缺货数却大幅减少61.3%。因此，考虑需求关联性，可使管理者在略微增加总运营成本的代价下，大幅减少缺货数量。

4.2 库存容量敏感性分析

库存容量限制是库存分配问题中的关键约束之一，为了分析库存容量变化对于结果的影响，进行10组算例，分别设置库存容量为1至10万件（产品的总需求量之和约为4万件），并对比考虑关联性与不考虑关联性情况下，产生的总运营成本以及缺货数，结果如图4和图5所示。

根据图4和图5可以得出：

a．随着库存容量的增加，缺货数逐渐减小，并趋于稳定，同时总运营成本会逐渐增大并趋于稳定。这是因为当库存容量较小时，库存量较低，导致低运营成本与高缺货数；而当库存容量增大时，库存量和订货量也随之增大，由此运营成本升高，而缺货数减少。

b．当库存容量较紧张时（低于4万件），考虑需求关联性反而会引起缺货数的略微上升；而当库存容量较为充裕时（超过4万件），考虑需求关联性可使缺货数显著减少。

c．当库存容量较紧张时，考虑关联性与不考虑关联性产生的总运营成本基本持平；当库存容量较为充裕时，考虑需求关联性会引起总运营成本的上升。

因此，当库存容量较为紧张时，考虑需求关联性反而会带来缺货数略微上升的负面影响，而当库存容量较为充裕时，考虑需求关联性才能实现缺货数的大幅减少，但同时也会引起总运营成本的升高。

4.3 关联规则挖掘置信度阈值敏感性分析

在关联规则挖掘中，置信度阈值决定着挖掘得到的关联规则数，为了分析关联规则阈值的设置对于结果的影响情况，进行4组实验。设置置信度阈值为1.0，0.9，0.8，0.7，分别挖掘得到关联规则数为0（对应不考虑关联性情况），3，16，57，并通过验证集计算产生的总运营成本和缺货数，结果如表4所示。

由表4可以看出：当置信度适中时，缺货数大幅减少，而总运营成本小幅增加；而当置信度偏低、关联规则数目过多时，缺货数减少率基本维持稳定，而总运营成本却会急剧增加。因此，管理者在进行关联规则挖掘时，需要选择合适的置信度，才能通过考虑关联规则获得较为理想的结果。在本文使用的数据集中，采用0.8左右的置信度较为合适。

4.4供应商个数敏感性分析

供应商个数是多供应商库存分配问题中的重要因素，不同的供应商具有不同的运输提前期和单位运输成本。此外，每个供应商还具有供应量上限约束，这些因素影响着库存分配的最终结果。为了分析供应商个数带来的影响，本文分别设置供应商个数为1-8个，在考虑需求关联性的条件下，计算产生的总运营成本和缺货数，结果如图6和图7所示。

可以看出，随着供应商个数的增加，总运营成本显著上升，同时缺货数大幅下降。当供应商数量超过5个左右时，总运营成本和缺货数都呈现稳定趋势。这是因为：当供应商个数较少时，由于存在供应量上限约束，前置仓的订货量也较小，此时总运营成本较低，但也导致了大量缺货现象的产生；当供应商个数增加时，前置仓可以大幅增加订货量，这将引起总运营成本的上升，但同时也能大幅减少缺货数。因此，增加供应商的个数，对于缺货数的减少具有较强的积极意义。

5 结论

研究了具有库存容量限制的多供应商电商库存分配问题，使用FP-Growth算法从真实数据集中挖掘得到关联规则，将关联规则抽象为一种约束，构建以最小化缺货数和最小化总运营成本为目标的双目标优化模型，并使用分段线性拟合方法对非线性的目标函数和约束进行处理。针对该模型，采用非支配排序遗传算法（NSGA-Ⅱ）对其进行求解，并通过“先知种群”的种群初始化方法对算法进行改进，使得算法收敛速度大幅提高。基于真实数据的数值实验和敏感性分析表明：

a．在库存分配问题中，考虑需求关联性的影响会导致后项产品订货量的增加，从而引起运营成本的小幅度上升，但同时可以大幅减少缺货数量。基于真实数据的算例分析表明，考虑需求关联性使得总运营成本上升2.3%，而使得缺货数量减少61.3%。

b．库存容量的充裕程度影响考虑需求关联性所带来的效果，当库存容量较为紧张时，考虑需求关联性带来的影响较小，只有当库存容量较为充裕时，考虑需求关联性才能使缺货数量大幅下降。因此，前置仓管理者应优先增加库存容量，再基于需求关联性进行库存分配优化。

c．在考虑需求关联性的库存分配问题中，需要设置合适的关联规则挖掘置信度阈值，过低的置信度阈值会引入过多的关联规则，使得总运营成本大幅上升。

d．随着供应商个数的增加，前置仓总运营成本会随着订货量的增大而上升，同时缺货数也会大幅减少，当供应商达到一定数量时，总运营成本和缺货数趋于稳定。

参考文献：

[1] ZHENG K N，ZHANG Z P，SONG B.E-commercelogistics distribution mode in big-data context：a caseanalysis of JD. COM[J]. Industrial Marketing Management，2020. 86： 154-162．

[2] FENG H L，WU Q，MUTHURAMAN K，et al.Replenishment policies for multi-product stochasticinventory systems with correlated demand and joint-replenishment costs[J]. Production and OperationsManagement， 2015， 24（4）： 647-664.

[3] SVOBODA J，MINNER S，YAO M.Typology andliterature review on multiple supplier inventory controlmodels[J]. European Joumal of Operational Research，2021；293（1）： 1-23.

[4] CHANG S C，CHANG C T.A multi-stage and multi-supplier inventory model allowing different orderquantities[J]. Applied Mathematical Modelling， 2017， 52：613-625.

[5] SONG J S.On the order fill rate in a multi-item， base-stockinventory system[J]. Operations Research， 1998， 46（6）：831-845.

[6] LIU L M，YUAN X M.Coordinated replenishments ininventory systems with correlated demands[J]. EuropeanJournal of Operational Research. 2000， 123（3）： 490-503.

[7] ZHANG R Q， KAKU I. XIAO Y Y. Deterministic EOQwith partial backordering and correlated demand caused bycross-selling[J] . European Journal of Operational Research，2011， 210（3）： 537-551.

[8] POORMOAIED S， ATAN Z. A continuous review policyfor two complementary products with interrelateddemand[J]. Computers & Industrial Engineering， 2020，150： 106980.

[9] YAZLALI O， ERHUN F. Dual-supply inventory problemwith capacity limits on order sizes and unrestrictedordering costs[J]. lIE Transactions， 2009， 41（8）： 716-729.

[10] SONG J S， ZIPKIN P. Inventories with multiple supplysources and networks of queues with overflow bypasses[J] .Management Science， 2009， 55（3）： 362-372.

[11] ZENG Y， YIN S Q， LIU J Y. et al. Research of improvedFP-Growth algorithm in association rules mining[J].Scientific Programming. 2015， 2015： 910281.

[12] LIN R H. Potential use of FP-growth algorithm foridentifying competitive suppliers in SCM[J] . Journal of theOperational Research Society， 2009， 60（8）： 1135-1141.

[13]粱泉，翁剑成.周伟，等.基于关联规则的公共交通通勤稳定性人群辨识 cJ].吉林大学学报（工学版）， 2019， 49（5）：1484-1491.

[14] XU F. Statistical measurement of the inventory shortagecost[J]. Journal of Applied Statistics， 2017， 44（4）：642-648.

[15]王林，顿彩霞，杨锐．基于混合差分进化算法和熵权TOPSIS的多目标（Q，r）库存模型[J]控制与决策．2011，26（12）： 1913-1916.

[16]任宏涛，郭颖，周文戟，等，资源约束下绿色铝供应链网络设计多目标优化[J]系统T程理论与实践，2020，40（8）： 2090-2103.

[17] LAGOS C，VEGA J，GUERRERO G，et al.Solving anovel multi-objective inventory location problem by meansof a local search algorithm[J]. Studies in Informatics andControl. 2016， 25（2）： 189-194.

[18]姜芳，郭健全．多目标多周期多阶段逆向物流网络动态联建[J].上海理工大学学报，2018， 40（3）： 274-281.

[19]张天瑞，魏铭琦，高秀秀，等，基于交互式模糊规划方法的可持续闭环供应链网络规划[J]．运筹与管理，2021，30（8）： 81-86.

[20] AGRAWAL R，IMIELINSKIT，SWAMI A.Miningassociation rules between sets of items in largedatabases[J]. ACM SICJMOD Record， 1993， 22（2）：207-216.

[21] ROSSI R，TARIM S A，PRESTWICH S，et al.Piecewiselinear lower and upper bounds for the standard normal firstorder loss function[J] Applied Mathematics andComputation， 2014， 231： 489-502.

（編辑：丁红艺）