探究图形语言在高中数学函数教学中的作用
2023-05-30李武
李武


【摘要】数学抽象性已经成为了高中生学习数学的一种阻碍,所以如何在教学中引导学生将抽象问题形象化就成为了教师数学教学研究的主要研究内容。在教学中要培养学生作图能力,注重作图的准确性和完整性,还要培养学生从题目抽象文字中挖掘其所隐藏的几何意义的能力等。
【关键词】图形语言;高中数学;培养动态思维能力
数学教学的主要目的在于培养学生的数学思维,引导学生用数学思维看世界。同时从公平公正的人才选拔角度来说,数学教学目的也重在培养学生解题能力,所以提高数学的解题能力就成为了教学重要环节。而数学的解题过程其实就是数学语言的转化过程,所以培养学生图形语言具有现实意义。
数学语言不是简单地描述数学知识,而是数学思维的一种载体和教学过程的交流工具。在教学活动中,很多抽象的数学概念、性质需要借助恰当的数学语言来呈现,课堂教学也需要借助数学语言来交流互动。因此,数学教学其实就是在教学过程中培养学生将数学语言之间的演变、转化和应用的思维形成过程。
数学图形语言可以将数学研究对象、性质、思想进行直观形象的描述。图形语言包括几何学中的各种平面和立体图形模型;包括概率学中的频率分布直方图、分布列表等,以及初等函数、三角函数这样函数的图像。可以说这些内容涉及的图形语言的本质就是数学语言的转化和应用,即在理解对象概念、性质的基础上,按照特定的法则对数学语言进行加工,最后以形象直观的图式呈现。
一、图形语言的教学价值
培养学生通过图形思考数学问题符合高中数学直观想象的核心素养。数学图形可以将数学研究对象、性质、思想进行直观形象的描述,有利于学生克服对数学的恐惧、加深对知识的记忆,提高解题能力等,所以图形语言具有重要的现实意义。
1.将抽象概念形象化激发学生学习兴趣。笔者通过教学实践发现,高中生之所以对数学产生恐惧和排斥的心理,主要原因是因为数学概念性质过于抽象。而中学生的思维还只处于想象思维向抽象思维过渡阶段,对于抽象概念很难直接通过自然语言去理解,而如果能借助图形语言将抽象概念形象化可以在很大程度上让学生很容易就从本质上掌握数学抽象概念,降低学生对数学的恐惧和排斥,激发学生学习数学的兴趣。
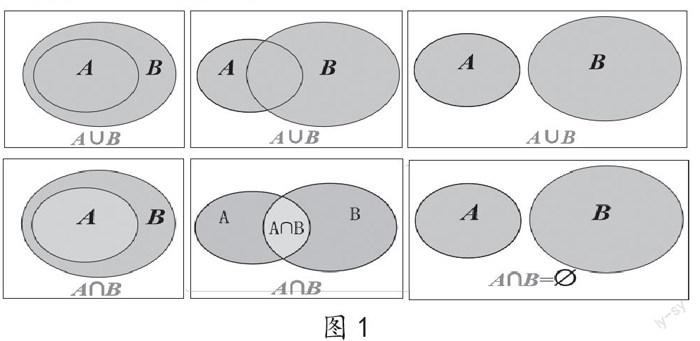
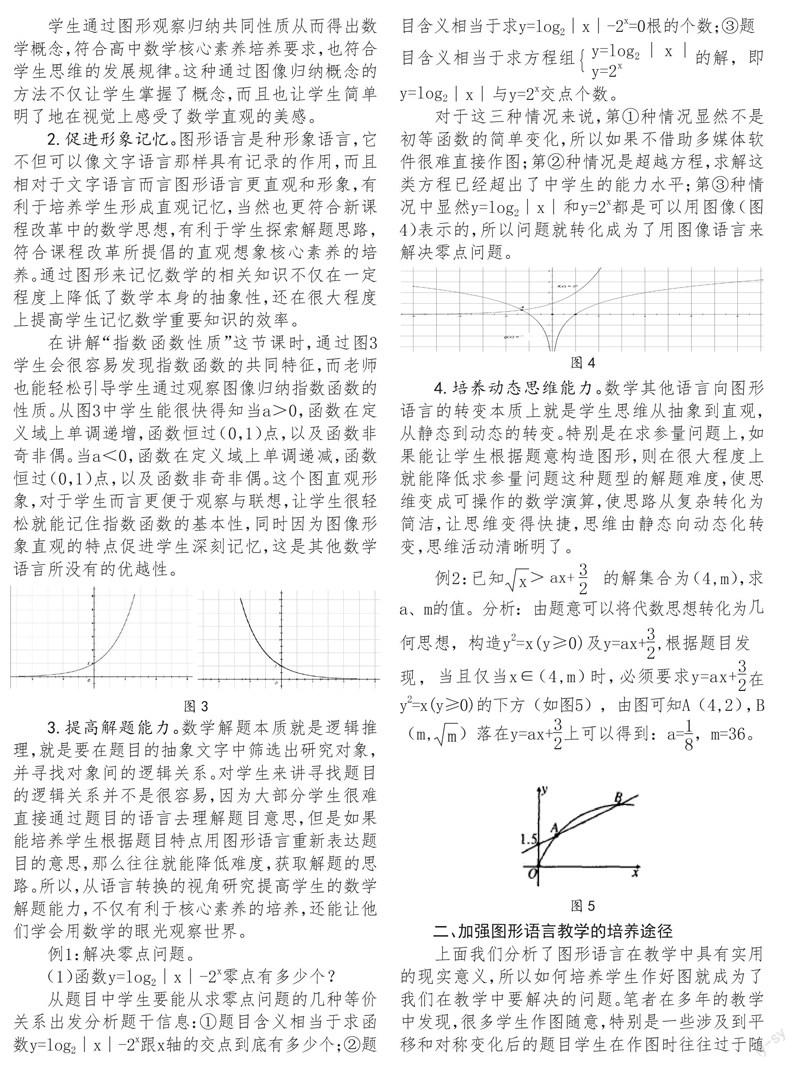
如图1,在“集合”这一小节中,我们可以利用韦恩图或者数轴法的图式语言来教学,运用韦恩图很显然使得交集、并集的抽象概念直观化,有利于帮助学生对概念进行理解和掌握。通过图式语言(图1)学生可以形象地发现补集、交集的准确概念,不仅降低了难度,对学生记忆也有了形象直观的帮助,在将来的解题过程中也能避免对概念的模糊记忆而做错题。
在讲“函数的单调性、奇偶性”等性质时,教师可以引导学生通过观察直观的图像入手,由浅入深,由具体到抽象层层递进展开。再引导学生通过图像语言得到文字语言或符号语言,这在一定程度上大大地降低了学习的难度,有利于帮助学生理解和掌握。如图2,学生很容易就可以从图像中得到单调函数定义的自然语言:在x的某一范围内函数值y随着x的增大而增大,或者在x的某一范围内函数值y随着x的减小而减小。
学生通过图形观察归纳共同性质从而得出数学概念,符合高中数学核心素养培养要求,也符合学生思维的发展规律。这种通过图像归纳概念的方法不仅让学生掌握了概念,而且也让学生简单明了地在视觉上感受了数学直观的美感。
2.促进形象记忆。图形语言是种形象语言,它不但可以像文字语言那样具有记录的作用,而且相对于文字语言而言图形语言更直观和形象,有利于培养学生形成直观记忆,当然也更符合新课程改革中的数学思想,有利于学生探索解题思路,符合课程改革所提倡的直观想象核心素养的培养。通过图形来记忆数学的相关知识不仅在一定程度上降低了数学本身的抽象性,还在很大程度上提高学生记忆数学重要知识的效率。
在讲解“指数函数性质”这节课时,通过图3学生会很容易发现指数函数的共同特征,而老师也能轻松引导学生通过观察图像归纳指数函数的性质。从图3中学生能很快得知当a>0,函数在定义域上单调递增,函数恒过(0,1)点,以及函数非奇非偶。当a<0,函数在定义域上单调递减,函数恒过(0,1)点,以及函数非奇非偶。这个图直观形象,对于学生而言更便于观察与联想,让学生很轻松就能记住指数函数的基本性,同时因为图像形象直观的特点促进学生深刻记忆,这是其他数学语言所没有的优越性。
3.提高解题能力。数学解题本质就是逻辑推理,就是要在题目的抽象文字中筛选出研究对象,并寻找对象间的逻辑关系。对学生来讲寻找题目的逻辑关系并不是很容易,因为大部分学生很难直接通过题目的语言去理解题目意思,但是如果能培养学生根据题目特点用图形语言重新表达题目的意思,那么往往就能降低难度,获取解题的思路。所以,从语言转换的视角研究提高学生的数学解题能力,不仅有利于核心素养的培养,还能让他们学会用数学的眼光观察世界。
例1:解决零点问题。
(1)函數y=log2∣x∣-2x零点有多少个?
从题目中学生要能从求零点问题的几种等价关系出发分析题干信息:①题目含义相当于求函数y=log2∣x∣-2x跟x轴的交点到底有多少个;②题目含义相当于求y=log2∣x∣-2x=0根的个数;③题
目含义相当于求方程组的解,即y=log2∣x∣与y=2x交点个数。
对于这三种情况来说,第①种情况显然不是初等函数的简单变化,所以如果不借助多媒体软件很难直接作图;第②种情况是超越方程,求解这类方程已经超出了中学生的能力水平;第③种情况中显然y=log2∣x∣和y=2x都是可以用图像(图4)表示的,所以问题就转化成为了用图像语言来解决零点问题。
4.培养动态思维能力。数学其他语言向图形语言的转变本质上就是学生思维从抽象到直观,从静态到动态的转变。特别是在求参量问题上,如果能让学生根据题意构造图形,则在很大程度上就能降低求参量问题这种题型的解题难度,使思维变成可操作的数学演算,使思路从复杂转化为简洁,让思维变得快捷,思维由静态向动态化转变,思维活动清晰明了。
例2:已知的解集合为(4,m),求
a、m的值。分析:由题意可以将代数思想转化为几何思想,构造y2=x(y≥0)及y=ax+,根据题目发
现,当且仅当x∈(4,m)时,必须要求y=ax+在y2=x(y≥0)的下方(如图5),由图可知A(4,2),B(m,)落在y=ax+上可以得到:a=,m=36。
二、加强图形语言教学的培养途径
上面我们分析了图形语言在教学中具有实用的现实意义,所以如何培养学生作好图就成为了我们在教学中要解决的问题。笔者在多年的教学中发现,很多学生作图随意,特别是一些涉及到平移和对称变化后的题目学生在作图时往往过于随意而导致最后出现错误,当然造成这种错误一定程度上是由于学生粗心,但同时也反映出学生对数学基本知识概念掌握不扎实,所以我们在引导学生作图时既要要求图像的准确完整,也要注重学生对数学定义定理的理解和掌握。
1.重视学生作图的准确性和完整性。图形语言虽然不能作为解题的步骤,但它为学生寻找解题方法和技巧提供了方向。可是在教学中我们经常发现学生因为作图时候过于随意最后出现了错误,所以在日常的作图训练中一定要重视学生作图的准确性和完整性。
例3:如图6,已知f(x)=∣2x-2∣-b有两个零点,则实数b的取值范围是多少?
分析:这个题目是零点问题,笔者在教学中发现很多学生虽然能把大概的图形画出来,但由于画得不准确,部分学生在画图过程中忽略了图形不能穿过y=-2,所以在x<1关于x对称以后在x<1部分的图形高度就超过了y=2的图形高度,得到的结果是b∈(0,+∞)。通过这个题目可以看出学生在画图时容易因为自己的不严谨使得画出的图形不够准确导致解题错误,所以在加强图形语言教学的培养中要重视学生作图的准确性和完整性。
2.培养学生发现问题中隐藏的几何意义。数学学习注重的是逻辑思维的转换,而图形语言就是将抽象思维向形象思维转变的载体,培养学生这种思维转变可以通过题目进行引导和解读,比如有些题目表面上是代数问题,可是其中却隐藏了丰富的几何意义,而引导学生挖掘其中的几何意义可以在一定程度上简化解题的过程,丰富解题技巧。
例4:在△ABC中,已知AB=,BC=2。求角C的取值范围。
常规解法1:在△ABC中,由余弦定理得AB2=
AC2+BC2-2AC·BCCOSC,所以3=AC2+4-4AC·COSC,即AC2-4AC·COSC+1=0。
由题,关于AC的一元二次方程应该有解,令△ABC=(4COSC)2-4≥0得COSC≥,或COSC≤-(舍去,
因为AB<AC),所以,0<C≤,即角C的取值范围是(0,]。
几何意义解法2:如图7,点A处在以点B为圆心以线段AB为半径的圆上,且不与CB处在同一条直线上。显然当AC与AB垂直时可得最大角∠C,此时sinC==C=60o,所以0<C≤。
3.提高学生的构图能力。在某些数学题目中,如果条件和结论之间存在着某些特定的几何意义,那么我们可以引导学生将问题转化为几何问题并构造出恰当的几何图形,从而使得问题简单化、形象化,做到化难为易。
例5:如图8,计算19981998×19971997-19981997×19971998这个代数运算其实就是两个矩形面积的差,即SABHG-SEDGF。
从这个简单例子中我们发现培养学生构图能力对有效促进学生掌握图形语言,增强数学思维具有重要的意义。
4.分层培养学生作图。如何培养学生的作图能力已经成为我们教学中要解决的重要问题。在教学上我们要因材施教,根据不同的学生设置不同的问题,从而提高课堂质量。
课堂教学中培养学生作图能力可以是老師示范引导,亦可以是学生自己动手。不论是采用什么方式,目的都是让学生在课堂上掌握准确的画图方式,哪怕是草图也不能出现原则性错误或者概念错误,比如图像的对称平移要能准确刻画。虽然一节课的内容和教学要求都是统一的,但作为教师应该根据学生的能力差异和认知水平差异,对不同层次的学生进行有针对性的教学。教师在培养学生作图能力时,需充分考虑学生的知识掌握水平来将问题按难、适中和容易三个层次进行设计。先是站在激发学生兴趣的角度设计问题,引导学生层层深入,帮助学生理清基本概念性质,再适时、适量地设计出若干问题,让不同层次的学生解答。其中,针对性强、巩固知识类的常见的图形提问,以基础差的学生为主,让全体学生回忆所学过的知识,提醒学生加强理解和记忆重点知识;比较复杂的不常见的图形提问,以优生回答为主,一方面可以拓展优生的能力,另一方面让优生带动其他学生拓宽思路。也可以引导学生根据内容相互提问,会让课堂更具趣味性与拓展性。只有在课堂中分层设置问题,灵活地运用提问技能,才有助于把课堂真正构建为师生互动的课堂,调动学生的积极性从而使其更加牢固地掌握数学基本知识,为提高数学作图能力奠定坚实基础。
总之,图形语言最大的特点就是直观性强,它可以让抽象思维具体化、繁琐问题简洁化,帮助学生分析题目、记忆知识点。此外,虽然图式语言不能作为解题或证明的依据,但它很多时候能给我们启发,而且我们大多数时候都要结合图像、图表等来分析题目。正如我国著名数学家华罗庚所说:“数形结合百般好,隔裂分开万事非。”
【参考文献】
[1]张珂.初中生数学语言转换能力及其培养策略研究[D].喀什:喀什大学,2019.
[2]王梓谕.初中生数学语言转换能力调查研究[D].沈阳:沈阳师范大学,2016.
[3]赵金荣.高中数学教学中学生解题能力的培养对策[J].理科考试研究:高中版,2016(11).
(基金项目:本文系海南省教育科学规划2021年度课题“基于深度学习的高中数学三种语言转化研究”的研究成果,课题编号:QJH202110070)
