图形语言在数学学习中的重要性

蔡鹏

摘 要：应用数学图形语言能简化文字记录，体现几何图形语言的优势，能够提高学生在数学语言表达和数学语言应用方面的能力，同时也能提高学生多元化运用、开发与实践的探索精神，因此，在数学教学过程中，教师应加强数学图形语言的研究和运用，进而促进学生的数学思维交流，规范他们数学语言描述。

关键词：数学;图形语言;重要性

中图分类号：G63     文献标识码：A     文章编号：1673-9132（2017）05-0196-02

DOI：10.16657/j.cnki.issn1673-9132.2017.05.124

分析近几年高考数学题型的变化，可以发现，考查学生解题能力的题目逐渐增多，因此，学生不能认为把基础知识学精通了，就算学好了数学，而是在此基础上更加注重知识的应用。数学图形语言的学习与应用在数学学习过程中有着举足轻重的作用，所以其重要性不容忽视。

一、接受知识上的重要性

（一）掌握数学图形语言是学好数学的前提

数学语言分为文字语言、符号语言和图形语言，它们在阐述数学问题时互相补充、互相印证，所以，掌握好数学中的各种语言是学好数学的前提。图形作为一种数学语言，以其直观性与形象性，支起了数学的半壁江山，它让学生体会到数学不仅仅只有严谨与抽象，而且在“图形”的照耀下，“冰冷的数学”彰显出了“生动的美丽”。

（二）掌握数学图形语言是接受新知识的前提

人教A版《数学》（必修2）中第1.1.1节《柱、锥、台、球的结构特征》，教材给出棱柱的相关概念为：“一般地，有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱……叫做底面……叫做侧面……叫做侧棱……叫做顶点。”学生对抽象的文字语言不能很好的理解其含义，我给出了具体的六棱柱模型，学生通过观察、体会图形，心中的困惑得以解决。在讲授之后的棱锥、棱台、圆柱、圆锥的定义及性质时，我采用了相同的方式，学生理解了概念内容，并且自己动手画出图形，找到相关的元素。通过这一节内容的学习，学生对图形解决数学问题的功能有了深刻的认识。

教授人教A版《数学》（必修5）中第1.1.2节《余弦定理》后，在引导学生推导余弦定理的具体内容时，如果不采用数形结合的方法，整节课就显得空洞、乏味，如果是画出图形，引导学生利用向量工具进行推导，教师推导其中一个，学生掌握方法后，其余两个可以让他们自己解决，并且他们在之后的正、余弦定理的应用中也能得心应手。

（三）握数学图形语言有助于发展学生的逻辑思维能力

因为数学知识的呈现离不开图形语言，所以要提高学生学习数学的能力，就必须提高他们图形语言的识别与应用能力，而学生仅靠课堂上听老师的讲授是远远不够的，只有通过阅读、模仿、应用课本上的呈现形式，才能规范自己的数学图形语言，提高自己数学图形语言的理解力和表达力，从而更好地进行数学交流，而且对自己的逻辑思维能力是很好的锻炼。

二、解决问题中的重要性

（一）掌握数学图形语言，在问题求解中会有事半功倍的效果

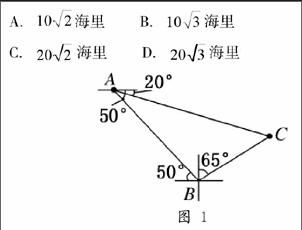
案例1.要求学生解决问题：一艘海轮从A处出发，以每小时40海里的速度沿东偏南50°方向直线航行，30分钟后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是东偏南20°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是（ ）

A.海里         B.海里

C.海里         D.海里

图 1

学生读完题目后，脑海里对题目中的点的位置、角度大小、航行方向几乎没有留下一点印象，因此，教师可以要求学生根据题意画出图形（图1），并将相关的量在图形中标注出来，之后再讨论求解，这样学生都能顺利求解。

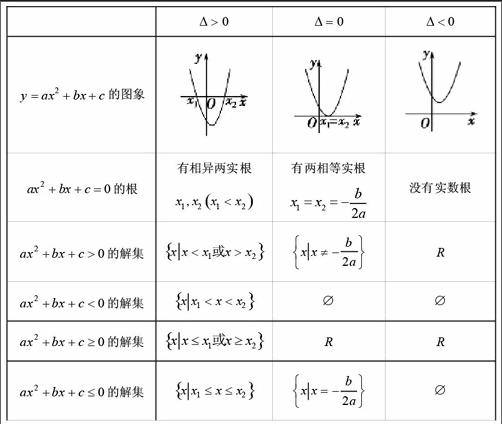
案例2.求不等式x2+2x-3>0的解集。

学生是第一次接触一元二次不等式的解法，所以给出题目后，他们都表示不会求解。为了能让学生迅速理解并很好地掌握这部分知识，我先引导学生揣摩一元二次方程、一元二次函数、一元二次不等式的关系，再通过采用数形结合的方法讲授，这样学生就能接受、理解，并会应用了。具体如下：

数学图形的学习与应用在高中数学学习方面起到了举足轻重的作用，它能够培养学生的数学图形思维，有效提高学生解决问题的能力与技巧，促使学生在高中数学学习上取得更大的进步，所以在平时教学中，教师要探索利用图形语言进行教学的方法，以便提高学生的抽象思维能力和数学解题能力。