生活中几种对角度估测的数学方法简析

2023-05-30钱杰

教育·教学科研 2023年3期

钱杰

一、问题的背景

生活中常常需要对一些数量进行估计，如在环境布置过程中对物体长度的估计；在菜场买菜时对菜的重量、价格的估计；在木工、钣金工作中对角度大小、图形周长、面积的估计。我们有很多测量的工具，也已经掌握了很多的计算方法来进行精确的测量计算，而在生活中，有经验的工匠经常能够通过最简单的工具、最基本的方法来对数量进行估测。

如对于本文将要介绍的，对角度的估测而言，其实我们完全可以借助量角器来测量，或者通过测量待测角所在直角三角形的边长，利用三角函数来计算，从而解决测量角度大小的问题。

本文主要介绍的是在没有量角器、不使用三角函数的前提下，如何估测一个角的大小。因为任意一个钝角都可以通过其补角计算得到，所以本文研究的对象是锐角。

二、问题的研究

通过搜索发现，生活中比较主流的角度估测方法主要有如下几种：直接估计、借助手掌估计、借助三角板估测、“以直代曲法”估测、“割圆法”估测、“构图法”估测。

直接估计主要依赖于经验，虽然十分方便，但通常误差较大，适用于对精度要求不高的情况；人体的手掌中蕴含着几个特殊角，如图1。借助手掌估计就是利用手掌张开时形成的角度大小来对待测角的大小进行估计，由于手掌张开的程度不同会直接影响角度的大小、摆放不方便等，借助手掌估计角度的大小同样会产生较大误差。

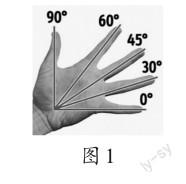
因此，本文主要简述其他四种估测方法的操作步骤及相关误差分析。

（一）借助三角板估测

前文提到，可以借助手掌对待测角进行大小估计，其中的误差主要来源于手掌对30°、45°、60°、90°的拟合程度、手掌的摆放方法以及观察者自身对角度大小的感觉。虽然这种估计方法误差较大，但它提供了一个估测角度大小的思路，即通过与已知角的大小比较来估计待测角的大小。

生活中，常见的确定角有平角180°、周角360°。但是仅通过这两个角来估计显然是不够的。因此，可以借助生活中常见的两把三角尺来对待测角进行估测。

常见的三角尺中，一把是等腰直角三角尺，它的三个内角分别为45°、45°、90°，另一把是以30°、60°、90°为内角的直角三角尺。因此，能够较为容易的估计30°、45°、60°、90°附近的角的大小。

同时容易想到的是，利用两把三角尺还可以构造一些特殊角：15°、30°、45°、60°、75°、90°。所有銳角中，15°的倍数角都可以由两把三角尺构造出来。这对缩小待测角的范围有很大的帮助，构造出的这些15°的倍数角可以把待测角的范围缩小在15°以内。如果稍加判断，可以将这个误差控制在10°以内。当然即使没有任何判断经验，也可以直接取范围两端的平均值。这样得到的估测值与实际值的误差不会超过7.5°。虽然误差仍然较大，但一定程度上已经能够给出相对准确的估计了。

（二）“以直代曲”估测法

在这种估测方法中，必须要用到圆规和刻度尺。

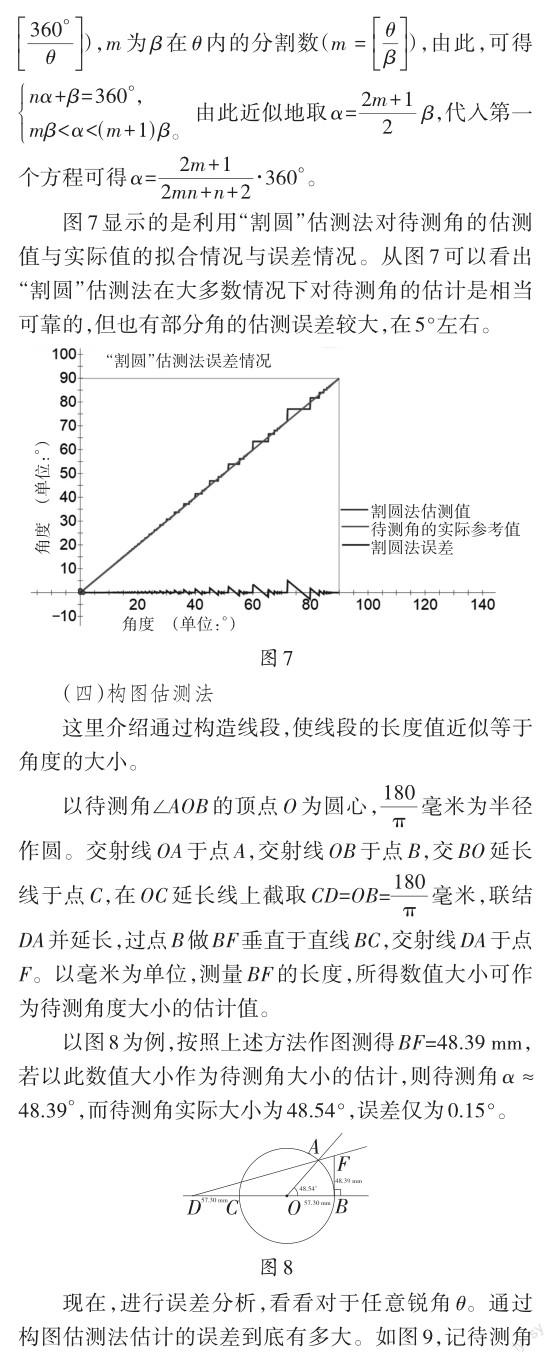
通过图像还可以发现，当待测角的度数不超过45°时，得到的误差是很小的。因此当估计较大的锐角时，往往可以先估计其余角或者半角来控制误差。

在实际作图过程中，通常以57.3 mm为半径作图。以这个精度作图所得到的待测角估计值和待测角的理论估计值几乎一致（棕色曲线被蓝色曲线覆盖，绿色曲线的纵坐标值几乎恒为0），如图11：

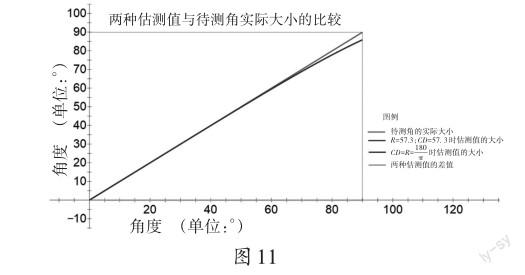
但是，对于一般作图而言，要精确到0.1毫米也是比较高的要求。以R=57，通过调整CD的大小，来观察不同的CD对误差的影响。得到结果如下图12：

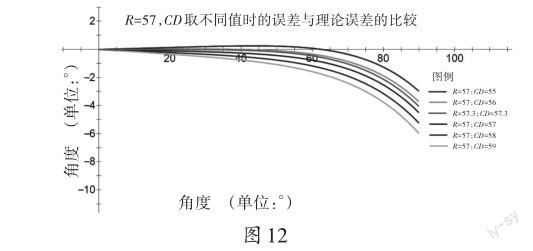
由此可见，在实际操作过程中如果将半径R定为57，那么在CD取56时，误差略胜于理论值误差；当CD取55时，若待测角的度数大于60°，则误差比理论误差要小得多，若待测角的度数在0°到60°之间，则其误差稍逊于理论误差。

因此建议，若通过估计待测角的余角或半角来确定待测角，那么可以用R=57，CD=56来进行构图估计；若直接估计待测角的大小，则可以用R=57，CD=55来进行构图估计。这样在作图时，半径、CD的选取更为方便，待测角的估计值也相对更优。

（五）小结

上文逐个分析了四类待测角的估测方法的操作步骤与误差情况，最后，再来看一看几种方法之间的误差比较。因为直接估计和利用手掌估计的误差较大，这里不做讨论。

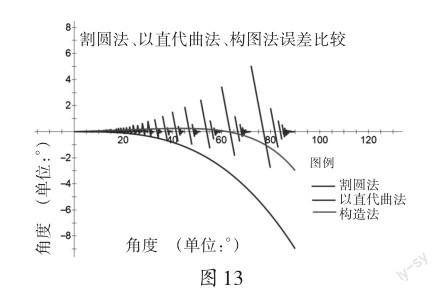
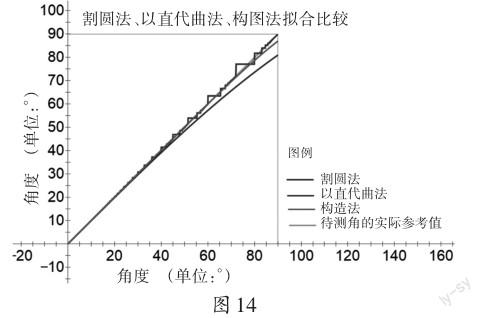
通过观察图13、图14容易发现，“割圆”估测法、“以直代曲”估测法、构图估测法三种方法在待测角小于45°时，估测结果都比较理想，其中构造法最佳，“以直代曲”法和“割圆”法不相上下。综合考虑作图难度与精度时，优先考虑构图估测法，其次“以直代曲”估测法，最后“割圆”估测法；在待测角较大，且不考虑半角和余角的情况下优先考虑构图估测法，其次“割圆”估测法，“以直代曲”估测法误差较大不做考虑；特别当估测角大于80°，接近90°时，优先考虑“割圆”估测法，其次构图估测法，“以直代曲”误差较大不做考虑。