数学+体育，实现“变教为学”

刘坤

［摘 要］随着课程改革的不断深入，人本精神备受青睐，据此，学者开展了大量的有关“变教为学”的研究。“变教为学”就是让学生成为学习的主体，学生通过合作探究、自主探索，发现并总结规律，而教学目标就是在一系列探究活动中达成的。

［关键词］变教为学；数学；体育

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2023）02-0053-03

“变教为学”的根本就是要实现师生的位置互换，让师生易地而处，主次分明，在明确一节课的教学内容后，教师要在教学中帮助学生积累数学活动经验和学习方法，让学生在操作活动中汲取知识养分。要达到这样的目的，深入研究课程标准和数学教育的文化渊源很有必要。

教师在挖掘知识内涵，联系新旧知识时，对于如何借机凸显数学知识的文化性，需要慎重对待。将文化情怀有机融入数学课程中，可以彰显数学的人文性。而将体育活动中的人文情怀融入数学课程中，则为数学教学的改革做了新的探索，是一个大胆的尝试，其价值体现在体育与健康密切相关，且体育学科更具话题性，也更能吸引学生。若将与体育有关的内容融入数学知识，学生的兴趣就会大增，可以更好地实现“变教为学”。笔者从引入体育活动的角度研究如何实现“变教为学”，以“圆的面积”“负数的认识”两课为例，浅谈如何将体育活动情境融入数学教学，以及如何通过体育活动渗透数学知识。

一、选择的情境要符合学科需求

学生是否可以自行完成学习目标，是衡量“变教为学”成功与否的标准。为了保障教学的顺利进行，教师需激起学生的学习兴趣。活动情境的选择是首要任务，情境要贴近生活，还要蕴含数学的人文气息。首先，筛选的体育活动要与数学知识密切相关，用体育活动去激发和带动学生的数学内需。为了达成目标，导入的活动情境要有可持续性，让学生能够带着一系列问题去研究情境。其次，“变教为学”是要让学生主动发现，因此，活动情境应该具有启发性，还要有线索，问题的解决过程要精彩，不断吸引学生追查下去，使学生在解决问题时体会数学思想的作用。下面笔者以“圆的面积”教学为例详细论述。

“圆的面积”的教学目标是使学生探索并掌握圆的面积公式，能用圆的面积公式解决简单的实际问题。这就需要教师物色合适的情境，情境既要引导学生提炼出圆的面积公式，又要让学生学会解决实际问题，一举两得。

对于“圆的面积”一课的导入情境，常见的情境是给一个自动洒水旋转喷头，让学生求洒水面积。学生经过探究发现，洒水区域是一个圆形，求洒水面积其实就是求一个圆的面积。这类情境难以持续制造话题，也难以激起学生的强烈兴趣。而笔者将导入情境设为足球赛情境，让学生求足球场的最佳场地面积。

情境：在足球赛中，每支球队配置11名球员（每队有1名守门员），1名球员运球耗时3秒，运球奔跑的速度约为5米/秒。根据以上条件，可以做出哪些判断？

学生首先算出1名球员运球奔跑的直线距离为5×3=15（米）。

接下来，让学生求出球场面积。通过集体讨论，学生会先确定球员运球的范围，再参考情境中所涉数据，进一步产生求圆的面积的想法。

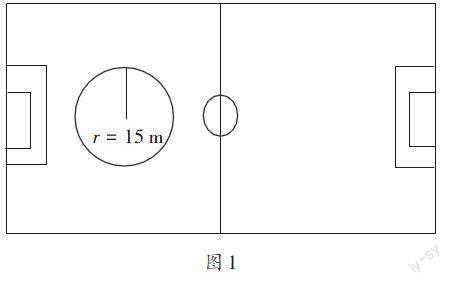
思考过程如下：1名球员运球奔跑的直线距离为15米，而球员奔跑的方向不确定，但他運球时应该不超出某个范围，这个范围应该是半径为15米的圆形（如图1）。

学生经历一步步环环相扣的缜密思考后，最终产生计算球员运球奔跑的范围的面积就是求圆的面积的想法。最终，学生利用圆的面积公式计算出球员运球奔跑的范围面积约是707平方米。

最后学生推算整个球场的面积。将每名球员运球奔跑的范围面积707平方米与球员人数10（除去守门员）相乘，得7070平方米，这就是科学规划的球场面积，如此才能保证球员自由运球而不互相掣肘。让学生上网查询数据，他们发现自己推算出的面积与标准的球场面积（7140平方米）相差不大。从这个情境中，学生深切体验到了数学方法的重要性，感受到了数学的人文内涵，而且获得了宝贵的解决实际问题的经验。

数学与体育本是不相关的两门学科，但是在这里却巧妙融合了，体育是学生喜爱的学科，其中足球运动较受学生的欢迎，当运用求运球的范围的情境来引起他们对计算圆形面积的兴趣时，学生就会对圆形面积的内涵有深刻体会：球员可带球奔跑的范围大小就是圆的面积，球员奔跑的直线距离为15米，那么这个圆的半径就是15米，此时，学生完成对圆形几何的抽象。学生要算清球员可带球奔跑的范围大小，只需计算出圆形面积即可，将动态化为静态，将体育化为几何，最后又回归到体育，将数学公式运用到体育中，利用1名球员的奔跑范围面积乘球员人数推算出足球场的面积，可谓取之于体育，用之于体育。

二、活动要体现数学知识的本质

在学科融合的过程中，要遵循数学知识原理，不能瞎编。因此，在设计与体育活动相关的情境时，就要慎重选择合适的活动。以“负数的认识”教学为例，对负数的认识是建立在对正数的深刻认识和重新解构上的。负数的出现打破了整数的局限，也扩充了数的外延。要让学生接受负数，就要让学生明白负数是社会生活的产物。因此，在设计活动之前，先回顾负数的历史。

从人类的社会活动看，生产经营中经常会出现盈亏、增减、买卖、出入、升降等现象。在记账时，盈利记为正，亏损记为负；在农业生产中，增产记为正，减产记为负。对这种意义截然相反的量，人们希望用具体的数字记录。由此可见，负数的出现是为了表示相反意义的量。

负数的另一种功能是表示小数减去大数的差，这一点可从《九章算术》查证，书中主要讲了方程组求解的问题，其中涉及小数减大数的问题，在采用消元法时，小数减大数不可避免，方程的解可能比0小，为了使方程有解，并且让小数减大数有结果，负数就问世了。

美国一家出版社出版的数学教材中大胆引用高尔夫球情境，将负数知识融入高尔夫球运动中。高尔夫球运动采用正负杆来表示成绩。通常18洞高尔夫球场的标准杆是72杆，即以72杆打完18个洞为标准成绩。比如，A运动员打完18个洞用了80杆，则记+8杆；B运动员打完18个洞用了70杆，则记-2杆，B运动员的成绩比A运动员的好。显然，当实际总杆数少于标准杆时，计分为负数，这揭示了负数的来源，即小数减大数之差。

情境为外衣，数学本质才是“贴身之物”，用其他生活情境来讲解正负数，学生不明白为何非要用正负数来表示相反的量，如温度，零上3℃、零下3℃为什么要用正负数表示。至于其他有相反意义的量，就更加牵强，比如向东走30米记为+30米，向西走30米记为-30米，原点就是0米。从原点出发，向东、向西走30米，都是距离延长30米，为何有正负之分，这个正负性是由方向决定的，与数字本身无关，也体现不出小数减大数等于负数这个原理。而高尔夫球运动则很好地弥补了上述不足，实际杆数比标准杆多，记为正数，实际杆数比标准杆少，记为负数，如+8杆和-2杆，这里的正负数就不是人为规定，而是由计算得出。

三、活動设计要深刻揭示知识起源

活动一：让学生查字典，检索汉字“正”“负”的含义。字典经常出现在语文学习中，也可以应用到数学中，将抽象的数学语言精确化。

活动二：让学生在具体情境中理解负数。教师出示高尔夫球运动的计分规则，列出2名选手打出的总杆数（标准杆为72杆），分别为74杆和70杆，让学生列式，计算出最终成绩，即（74-72）分和（70-72）分。学生发现70-72这个算式的结果不一般，必须用新的数来表示，即-2，读作“负二”。这一学习活动不仅让学生认识了一项新的体育运动，而且体现了负数的作用。

活动三：让学生观看一段高尔夫球比赛视频。教师出示各选手的成绩，让学生先比较他们的成绩，再给选手排名。然后分析成绩与名次的对应关系，看看与一般比赛的排名规则有什么区别。通过这个活动，可以帮助学生掌握负数的大小概念。

活动四：让学生尝试在数轴上标出各选手的成绩。这一活动的目的是让学生借助数轴熟悉数字的排列规则以及大小顺序，还有数字0的特殊性。在课堂尾声，回顾负数的发展史，让学生再次体会负数的本质。

活动二、三、四用高尔夫球运动来串起，既揭示了负数的意义，直指教学目标，又融入了数学文化内涵。这样的教学设计，从选材到点明主旨都披着体育活动的外衣，可成为“变教为学”的案例，也为体育与数学之间的学科融合提供了有价值的参考。这样的设计思路可以让学生大开眼界，并开拓思维。

披着体育的外衣，行数学之实，这是高明之举。体育运动的程序性和数学的逻辑性刚好合拍，当学生顺着体育活动的进展不断开发新情境时，对数学知识的钻研就会步步深入，可以说此时数学知识已经和体育运动有了深度捆绑。比如，当学生研究高尔夫球运动员的成绩排名时，自然会探究正负数的比较和负数的比较，知识得到进一步拓展和深化。如-3杆和-5杆，哪个杆数少？-3杆代表比标准杆（72杆）少3杆，即69杆；-5杆代表比标准杆少5杆，即67杆，因此，-5杆少于-3杆。同理，+7杆和-7杆，+7杆代表比标准杆（72杆）多7杆，-7杆代表比标准杆（72杆）少7杆，-7杆少于+7杆。继续推广，因为标准杆的存在，少于标准杆的杆数一定会比多于标准杆的杆数少，那么负数小于正数。一套比较成绩的方法就可以将正负数的大小囊括进去，可谓简明又方便。

小学生的思维处于形象思维阶段，具体可感的动作记忆是所有记忆形式中最深刻的，学生大都喜欢体育，因为体育不但具有游戏娱乐性，而且体育活动中的体验式认知带给学生经久不衰的记忆，这些动作记忆会化成一种潜意识和思维本能，一旦将数学知识融入体育活动中，学生因为对体育活动的好感和自带的运动潜能迸发出的探究热忱，就能最大化地吸收和消化数学知识。

［ 参 考 文 献 ］

[1］ 张青.学科融合，给学生不一样的体育学习：以数学进入《肩肘倒立》一课例谈[J].小学教学研究，2021（2）：24-25，27.

[2］ 郝研.探究核心理念下小学数学与体育教学的有效结合[J].华夏教师，2019（19）：29-30.

[3］ 位惠女.没有围墙的数学课堂[J].小学教学（数学版），2021（Z1）：132-135.

[4］ 邵征锋.对小学数学核心素养的开放性慎思[J].中小学教师培训，2021（10）：47-51.

[5］ 何长梅.学科融合背景下的小学数学欣赏性文化拓展课程研究[J].小学教学参考，2021（26）：32-33.

（责编 黄 露）