基于GA-SVR的疫情下各省粮食产量模型研究

童晓星 孟梁 张凌志

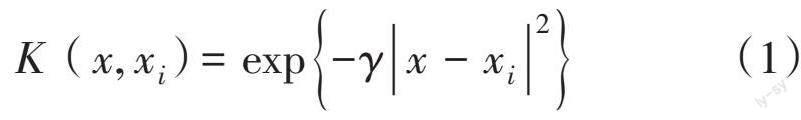
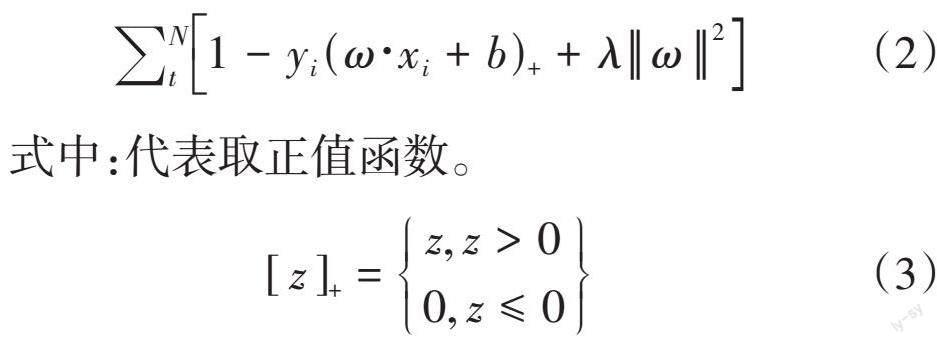
摘要 利用ε-SVR（支持向量回归）的理论，提出了一种大型传染病对当年各省粮食产量影响的模型，通过选取感染人口占比、近5年播种面积等16个因素，用1961—2020年被戊型肝炎、霍乱、严重急性呼吸综合征（SARS）和新冠肺炎影响的北京等52省（市、自治区）粮食产量数据进行建模，通过GA（贪婪算法）对核函数参数进行局部最优取值，当核函数中的γ值取值0.031、惩罚系数C取值5.0E+4、损失函数参数P取值0.000 98时，模型拟合平均相对误差0.92%，决定系数0.99。应用该模型对2020年被新冠肺炎疫情影响到的浙江、湖北省，2003年被SARS病毒影响到的甘肃、陕西、广东省以及1978年被登革热影响到的广东省的6组产量数据进行预测，平均相对误差为3.12%。为衡量大型传染病对粮食产量的影响程度，对去除感染人口占比和死亡人口占比2个因素后重新建模，新模型拟合平均相对误差为0.97%，预测平均相对误差为3.52%，表明大型传染病对粮食产量有一定的影响，但影响较小。基于GA-SVR的大型传染病对国内粮食产量影响的模型可有效预测疫情下当年各省粮食产量，为短期内地区粮食产量预测提供了新方法，也为国家宏观调控提供了新依据。

关键词 支持向量回归；大型传染病；当年各省粮食产量；贪婪算法；预测

中图分类号 T18；S114   文献标识码 A

文章编号 1007-7731（2023）06-0055-05

2020年初，全球暴发了新冠肺炎疫情，由于新冠病毒传染力强，导致传播范围广、感染人数多。2020年4月初，全球多国发布申明，为确保本国粮食供给，停止粮食出口。在疫情下，准确预测当年粮食产量可以帮助国家或地区更好地掌握农业生态发展趋势、保障人们生活的基本要求。虽然当前已有不少粮食预测的方法，如Nerlove模型[1]、系统动力学模型[2]、IPSO-BP模型[3]、时间序列模型等[4]，但对于大型传染病疫情下的地区粮食产量预测的研究仍然较少。

近些年来，随着人工智能、机器学习技术的发展，SVM支持向量机这种具备较强泛化能力和广泛适用性的算法已被普遍应用到农业生产预测、分类和图像识别等领域，如滴灌灌水器流量预测[5]，玉米、大豆、水稻识别[6]，现代农业气象分析[7]，灌溉耕地研究[8]，茶园地形数据研究等[9]，而SVM最终解决的是凸二次规划问题[10]，在处理局部极限极值的问题上优于神经网络。在本次研究课题中，由于新冠肺炎疫情的发生，存在个别地区暴发较严重，个别地区暴发较缓和等特点，SVM算法更易得到全局最优解。传统的SVM算法仅局限于二元分类，ε-SVR是在傳统二元分类的基础上可对回归问题进行拓展的算法[11]。

1 理论基础

1.1 SVR及其核函数

SVM作为一种二值分类模型（非0即1），模型建立在特征空间上的间隔最大的线性分类器之上，为使SVM可对连续性数值作回归预测，通过多次分类迭代的方式优化后提出了SVR模型。本文经过多次试验，确定径向基函数（RBF）为本数据建立模型的最佳核函数。相关计算公式如下：

径向基分类器的特点是每个基函数的中心对应于一个支持向量，输出权值都是由算法自动确定。其内积函数类似人脑的神经中枢特性，不同的S参数值相应的分类面差别较大。

Christopher J. C. Burges曾对线性核函数、多项式核函数和径向基核函数进行了试验比较，不同的核函数对不同的数据库各有优劣[12]，也有基于UCI基准库上的数据分析的研究表明径向基核函数性能略为优良 [13]。

1.2 核函数中重要参数γ、C、P

γ：设置核函数中γ的值，随着γ的增大，存在对于测试集分类效果差而对训练分类效果好的情况，并且容易泛化误差出现过拟合，一般取值在0.01[14]附近。本文通过迭代运算，得出最佳值为0.031。

C：惩罚因子。C表征对离群点的重视程度，C值大时对误差分类的惩罚增大，C值小时对误差分类的惩罚减小。本研究中由于样本较小，而大规模传染病造成的影响不可忽视性，故C值取值较大，当取值5.0E+4时，模型预测值和原始值的拟合度最高。

P代表SVM中损失函数中的参数b。SVM中的损失函数定义为合页（hinge）损失函数和正则化项之和，可用以下公式表示：

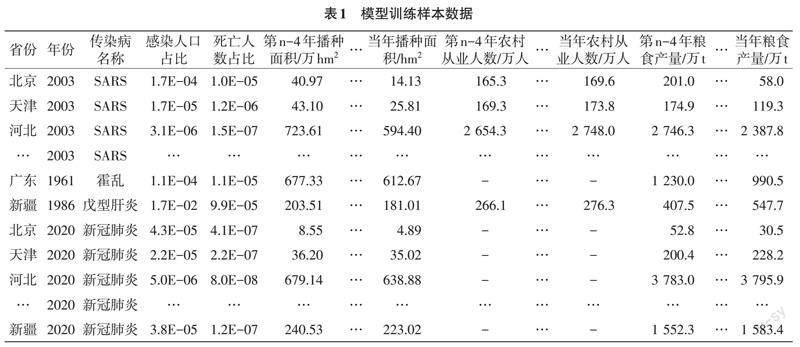
式中：代表取正值函数。

如果被正确分类，则损失为0，如果未被正确分类，则损失为z，[λω2]为了防止过拟合，进而增强泛化能力，合页损失函数表示预测不正确的类别（[i≠j]）累加之和，而参数b代表着损失阈值，b值越高，损失计算越高。

1.3 GA（贪婪算法）

本文通过GA算法实现SVR核函数中γ、C、P的选值，GA算法旨在某个范围内取最优解，而不是全局最优解，通过对γ分成0～0.001、0.001～0.01、0.01～0.1、0.1～1等4个范围，C分成0～0.1、0.1～1、1～10、10～100、100～1 000、1 000～1.0 E+4、1.0 E+4～1.0 E+5共7个范围，P分成0～1.0E-5、1.0E-5～1.0E-4、1.0E-4～1.0E-3、0.001～0.01、0.01～0.1、0.1～1共6个范围，γ、C、P的默认值分别为0.1、1、0.1，设置GA的第1个节点为改变γ的取值，分别取值0、0.001、0.01、0.1、1，第2个节点为C的7个取值，第3个节点为P的6个取值，这样平均误差最小的即为最优的γ、C、P的取值/取值范围。这里，对C的取值需要特别注意，以往对于C值的取值往往是遍历、迭代的方法，通常C越大说明错误惩罚越高，得出的模型拟合度高，容易出现过拟合的情况，这种情况对于新数据的适用性较低。本文通过GA算法，得出在C在一定闭合区域下的最优解，避免过拟合的现象。

2 粮食产量预测模型

2.1 训练样本

本文选取2020年新冠肺炎疫情期间的北京、天津等29个省（市、自治区），2003年SARS期间发生传播的北京、天津等21个省（市、自治区）粮食产量数据，1961年霍乱发生传播的广东省粮食产量数据以及1986年戊型肝炎发生传播的新疆维吾尔自治区粮食产量数据作为训练样本。2020年山东、广东新冠肺炎病毒感染人数分别达10 165人、12 624人，2003年北京SARS病毒感染人数达2 434人，1961年廣东省霍乱感染人数达4 319人，1986年新疆戊型肝炎感染人数达119 280人，传染病感染绝对数较大，可验证模型的广泛适用性。

2.2 预测样本

本文选取了2020年新冠肺炎期间的浙江、湖北省，2003年SARS疫情期间的广东、陕西、甘肃3个省份粮食产量数据以及1978年登革热疫情流行的广东省粮食产量数据作为预测样本。2020年湖北新冠肺炎病例达6.8万，1978年广东登革热病例达2.2万，比较能验证模型的适应性。

3 数据预处理与方法分析

3.1 数据预处理

根据现有研究，对于机器学习方法研究粮食产量的影响因素，主要考虑粮食作物播种面积、化肥施用量、粮食作物有效灌溉面积等因素[15-16]。考虑到本文主要是研究疫情下的粮食产量预测，故加入了疫情程度因素和当地务农人数（农村从业人员数）及变化趋势，近些年粮食产量发展趋势可涵盖化肥施用量等其他次要因素。

综上，本文将主要因素归为以下4类：①疫情影响力。由于各省份的人口数存在差异，故感染人口和死亡人口2个维度不能准确说明疫情的严重性，所以选取了感染人口和死亡人口占年底总人口数的比重作为疫情严重程度的指标；②粮食播种面积因素。近些年根据政策播种面积有所变化，带来的粮食产量影响也是很直观、明显的，所以选取了近5年的粮食播种面积；③务农人口。此处用“农村从业人口”来代替，近5年的农村从业人口可更好地反映务农人口变化趋势；④当地粮食产量。前一年当地粮食产量可作为当年粮食产量预估的最直接依据之一，为了更好地体现粮食产量变化的趋势，选取了近4年的当地粮食产量数据。

对本模型建立的数据处理如下：①感染人口和亡人口占比2个参数。由于疫情差异，如2003年SARS时期辽宁仅3例，而1986年新疆戊型肝炎发病近12万例，为体现不同地区疫情影响程度的差异，对该2个参数保留原格式；②粮食播种面积、农村从业人口。以第n-4年的粮食播种面积和农村从业人口作为基准，对第n-3年、第n-2年、第n-1年和当年的数据做归一化处理（如疫情发生在2000年，则第n-4年、第n-3年、第n-2年、第n-1年和当年分别代表1996年、1997年、1998年、1999年和2000年）；③粮食产量。以第n-4年的粮食产量作为基准，对第n-3年、第n-2年、第n-1年的产量做归一化处理。模型训练样本数据见表1。

3.2 方法分析

经过试验，通过GA算法对核函数参数取值，当γ在0.01～0.1、C在1.0E+4～1.0E+5和P在1.0E-4～1.0E-3范围内，平均相对误差最小，再进一步调整，当γ=0.031时，训练样本平均相对误差在2%左右，当γ>0.031并逐步增大时，训练样本平均相对误差仍然在2%左右，但预测样本平均相对误差明显增大，当γ<0.031并继续减小时，训练样本平均相对误差逐步上升，说明拟合度下降。

对惩罚因子C进行调整，当C<1.0E+4时，训练样本平均相对误差在5%左右，且C越小拟合度越低，当C>1.0E+4并逐步增大时，训练样本平均相对误差逐步减小，当C取值5.0E+4时，训练样本平均相对误差为0.92%，预测样本平均相对误差为3.11%，当C取值>5.0E+4且继续增大时，训练样本平均相对误差略微减小，但是预测样本平均相对误差的增加幅度较大，说明预测效果下降。

P代表对损失函数中的参数b，对P进行调整，当P>0.000 98且逐步增大时，训练样本平均相对误差逐步变大，拟合度下降，当P<0.000 98且逐步减小时，训练样本平均相对误差逐步变小，但预测样本平均相对误差的增加幅度较大，说明预测效果下降。

4 预测样本当年粮食产量预测结果

事实表明，当γ=0.031、C=5.0E+4、P=0.000 98时，模型拟合度较好，训练样本的平均相对误差为0.92%，决定系数达0.99，同时预测样本平均相对误差为3.11%，满足对传染病发生当年的地区粮食产量预测需求，而GA-SVR由于其对少量样本的案例模型建模，可通过参数优化设置，使其泛化能力较强，所以基于GA-SVR的粮食产量模型可对地区短期粮食产量预测提供准确的参考数据。训练样本结果见表2，预测结果见表3。

为了研究大型传染病是否对当年的粮食产量具有重大影响，本文对于原有样本去除疫情程度的2个参数（感染人口占比、死亡人数占比）后再次进行建模发现，训练样本拟合平均相对误差为0.97%，预测样本平均相对误差为3.52%，决定系数同样达到0.99。事实表明，该模型对地区短期粮食产量预测同样具有较好的参考性。含疫情因素和不含疫情因素预测结果见表4。

5 大型传染病对粮食产量的影响

由于国内大型传染病样本有限，属于小样本数据分析，GA-SVR方法对于少量样本拟合、泛化能力均较优秀，通过参数的优化设置，模型建立和验证得到以下结论：①在γ=0.031、C=5.0E+4、P=0.000 98时，模型可以较好地对样本数据进行拟合，预测效果也比较好，说明基于GA-SVR的大型传染病粮食产量模型准确、可靠。②在除去表示疫情程度的感染人口占比和死亡人口占比2个参数后重新建模，新模型仍然可以较好地对建模样本数据拟合，对目标样本进行预测，虽然较含疫情参数的模型平均相对误差略大，但在基于现有国内大型传染病疫情数据建模，疫情对当年地区粮食产量的影响有限。

该方法可以在大型传染病疫情环境下，提供当年各省粮食产量预测，为国家粮食宏观调控提供参考。

6 参考文献

[1] 李东林，左其亭，张伟，等.基于Nerlove方法的塔里木河流域农业水资源配置模型[J].水资源保护，2021，37（2）：75-80.

[2] 王倩，黄凯.基于系统动力学的北京市农业水足迹模拟与影响因素分析[J].系统工程，2021，39（3）：13-24.

[3] 胡程磊，刘永华，高菊玲.基于IPSO-BP模型的粮食产量预测方法研究[J].中国农机化学报，2021，42（3）：136-141.

[4] 李桐，董维红，张琦琛，等.基于时间序列模型的黑龙江省粮食水足迹分析与预测[J].排灌机械工程学报，2020，38（11）：1152-1159.

[5] 郭霖，白丹，王新端，等.基于支持向量機的滴灌灌水器流量预测模型建立与验证[J].农业工程学报，2018，34（2）：74-82

[6] 梁继，郑镇炜，夏诗婷，等.高分六号红边特征的农作物识别与评估[J].遥感学报，2020，24（10）：1168-1179.

[7] 李颖，陈怀亮.机器学习技术在现代农业气象中的应用[J].应用气象学报，2020，31（3）：257-266.

[8] 陈晓璐，王彦芳，张红梅，等.基于ESTARFM NDVI的察汗淖尔流域灌溉耕地提取方法研究[J].中国生态农业学报（中英文），2021，29（6）：1105-1116.

[9] 熊皓丽，周小成，汪小钦，等. 基于GEE云平台的福建省10 m分辨率茶园专题空间分布制图[J].地球信息科学学报，2021，23（7）：1325-1337.

[10] VAPNIK V N.The nature of statistical learning theory[M].New York：Springer，1999.

[11] 冼广铭，曾碧卿.ε-支持向量回归机算法及其应用[J].计算机工程与应用，2008（17）：40-42.

[12] BURGES C J C.A tutorial on support vector machines for pattern rec-ognition[J].Data Mining and Knowledge Discovery，1998（2）：121-167.

[13] 林升梁，刘志.基于RBF核函数的支持向量机参数选择[J]. 浙江工业大学学报，2007（2）：163-167.

[14] 成鹏，汪西莉.SVR参数对非线性函数拟合的影响[J].计算机工程，2011，37（3）：189，191，194.

[15] 高心怡，韩飞.基于混合智能算法的支持向量机的粮食产量预测[J].江苏大学学报（自然科学版），2020，41（3）：301-306.

[16] 伍丹华，周礼梅.基于BP神经网络的粮食产量预测[J].农业工程技术，2020，40（27）：51-53.

（责编：张宏民）

基金项目 国家自然科学基金项目（41877425）；上海市自然科学基金项目（21ZR1446800）。

作者简介 童晓星（1983—），男，浙江慈溪人，硕士，讲师。研究方向：农业电气化与自动化。