基于模糊神经网络的电动汽车变速器故障检测研究
2023-05-28鲁明旭曹宇
鲁明旭,曹宇
(上海城建职业学院 人工智能应用学院,上海 201415)
引言
变速器作为电动汽车中不可或缺的重要部件,随着科技的日新月异与工业的迅猛进步,变速器的设计与制造技术持续上升,变速器的构造愈来愈繁琐,故障的原因及现象也呈现多元化、不可控等趋势,所以正确地诊断电机故障并及准时地修复故障具有重大含义。
何雷等用LMD 与BP 神经网络方法对变速器的故障进行诊断,该方法将噪音协助解析法、部分平均值转化法和BP 神经网络相互融合,提高故障诊断的正确率,但采集故障输入信号的过程十分复杂[1];吴又新等提出基于遗传算法及样本熵优化VMD 参数的故障诊断方法,以建立的WOA-KELM 故障识别模型为基础,将样本熵优化VMD 参数加入遗传算法中从而诊断变速器故障,虽然此方法样本熵的维度小,但识别诊断变速器故障精度较低[2]。
由于汽车变速器的复杂结构,在其故障原因认知、不同故障信号获取以及分析故障中存在诸多模糊性问题,所以传统的故障诊断方法未能为我们提供实质性的故障分析。为避免现有研究的劣势,及变速器故障的模糊性,模糊诊断技术成为解决此类模糊问题实为不二之选。其中由模糊诊断技术和神经网络组成的模糊神经网络,既具备处理不确定性问题优势,又具备较强的自适应学习能力,可作为解决模糊诊断问题首选。因此本文提出基于模糊神经网络的电动汽车变速器故障检测方法,提升电动汽车变速器的故障诊断准确率,从而获得高效率的故障诊断。
1 基于模糊神经网络的电动汽车变速器故障检测
采用模糊神经网络对电动汽车变速器故障检测的过程中,需要先了解变速器的故障原因及故障现象,在此基础上进行电动汽车变速器故障检测研究。
1.1 电动车变速器的故障原因以及故障现象
1.1.1 电动车变速器的故障原因
通过变速器中变速杆方位信号、进气压力信号、发动机信号、节气门信号、车速度信号、变速器主轴转动速率以及冷凝温等信号,电动汽车即可展现自动变换挡实时掌握、变矩器的固定、安全失效庇护和故障暴露以及自判断等性能[3,4]。当以上所提信号出现异常时,自动变速器的故障现象也随之产生。
1.1.2 自动变速器的故障现象
自动变速器故障主要分为液压系统、电子系统和机械方面三大故障。液压系统故障包含油路压强过低、ATF 油质变等;电子系统类故障由换挡电磁阀、压迫掌控电磁阀以及车速传感器等类故障构成;制动器及调压阀故障和离合器消耗及滑出故障等属于机械方面故障。
1.2 模糊诊断技术
生活中经常会有无法阐述基本概念的模糊消息,为解决此类模糊消息,模糊思维应运而生。以下是模糊思维解决模糊消息的4 个步骤。
1)创建准确模糊集合:通过多样模糊准则创建不同角度描述模糊集合,模糊化的进程用详细数字描述。
2)建立输入参量:在模糊准则设置的基本要求下,建立变速器油路故障模型的输入参量。
3)明确隶属度:通过隶属度函数和模糊准则的输出结果,分别构造输入信号隶属度以及模糊集合。
4)获得结果:采用去模糊化管理所创建的模糊集合,获取需求的结果。
1.3 BP 神经网络概述
BP 神经网络是一种多层型神经网络,该网络被多数领域所采用,比如函数逼近、模式辨识及归类等。因为BP 神经网络中的传输函数可使用非线性函数,所以对汽车变速器故障检测具有显著效果[5]。BP 神经网络由输入层、隐含层以及输出层构成,一定数量的节点存在每一层中,除层内节点之间,权重矩阵W 将层和层间的节点相互关联;每个偏移量对应每个节点,这些节点的全部偏移量则组成一个偏移向量B。偏移向量B 和权重矩阵W 作为两个重要参量存在BP 神经网络中,因此,找寻恰当的的模型参量W、B 是实现BP 神经网络输出最佳结果的重要保障。图1 表示BP 神经网络结构。输入向量组和输出向量组分别用 P= [p1, p2,...,pn]以及Y=[y1, y2,..., yn]描述; wij、 wjk、 bij和 bjk分别表示输入层权值、隐含层的权值、输入层阈值以及隐含层阈值。通过BP 神经网络进行汽车变速器故障检测,离不开收纳训练样本、构建神经网络、训练神经网络以及测试神经网络4 个方面。
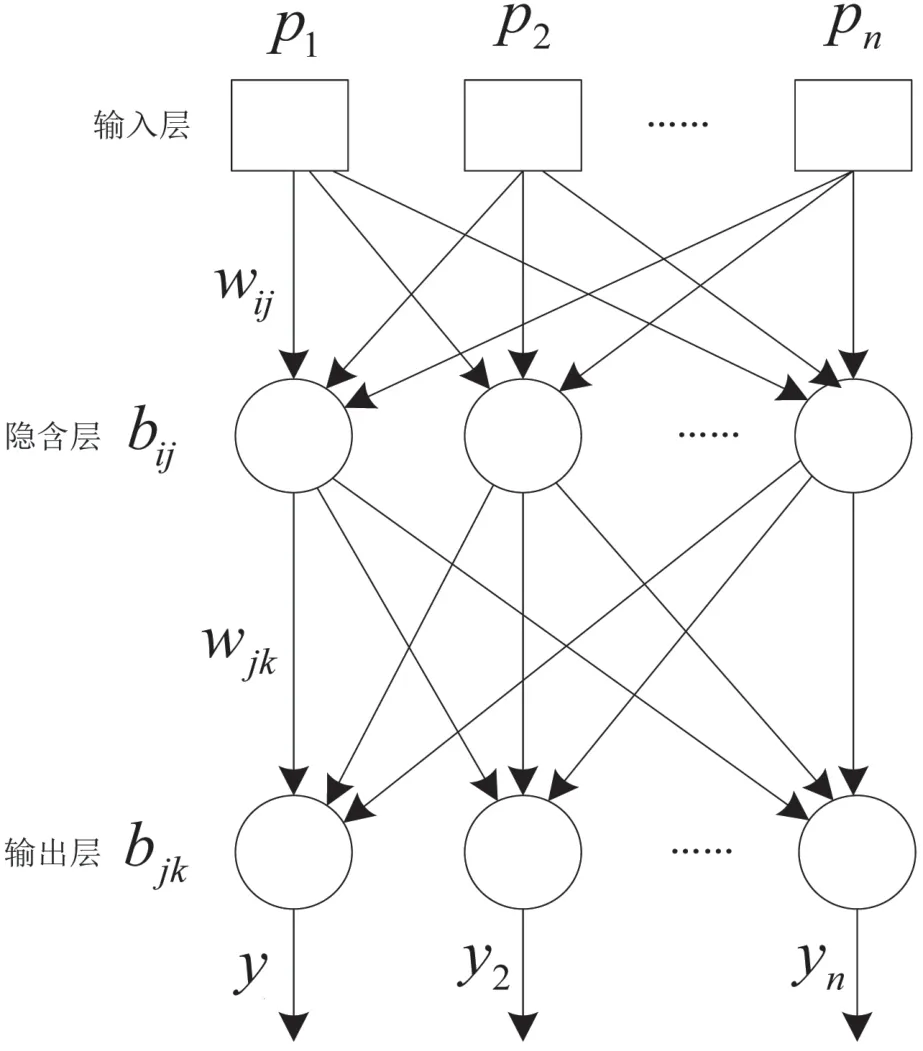
图1 BP 神经网络的结构
1.3.1 BP 算法训练流程
BP 神经网络训练流程由两方面构成,一方面是正向计算,另一方面是反向计算[6]。
1)正向计算
训练样本在正向计算中以输入层为起点,输出层为终点,流经全部BP 神经网络。通过计算上一层的输入与相关模型参量,获取每一层各个神经元的激活值。通过公式(1)可得正向计算中隐含层和输出层神经元激活值, hi、分别代表第i 层网络所含的节点数目以及第i层第j 个神经节点的激活值;第i 层第j 个神经元的移位值和第i 层第k 个神经节点与第i+1 层第j 个神经节点的权重系数分别用、描述。隐含层与输出层的激活函数分别使用sigmoid 和softmax 函数。
2)反向计算
通过反向计算中输出层激活值和训练样本标识对比获取误差值,对相关W 和B 采用梯度下降法进行修整并使误差以降低的角度前进[7,8],其次将误差通过每一层反向递进的方式来修改每一层的模型参量。通过公式(2)可算出反向运算中隐含层和输出层的节点误差值。样本点标识值用zj描述,该值会和输出层的激活值进行比对,隐含层与输出层激活函数的导函数分别是sigmoid 和softmax。
式中:
通过已获取的每个神经元误差对相关的网络参量开始修整,使用公式(3)确定W 和B 的更新规定,在整理算法的收敛速率过程中,迭代的次数和学习率分别用t和η 描述。
1.3.2 确定隐含层神经元数量
在BP 神经网络中,隐含层神经元个数对其输出的结果精确及范围产生不可忽略的影响[9]。隐含层神经元数、输入层神经元数和输出层神经元数分别是m、n 和l,取整函数采用round。确定隐含层神经节点数的方式是公式(4):
本文选取上述公式中一个,用公式(5)表示,以此确定隐含层节点数,通常选取较小数为隐含层神经元数。
1.4 变速器油路故障诊断模型
将变速杆方位信号和发动机转速信号作为变速器油路故障诊断模型中的输入信号,油路压强数值和油路液面位置为输出信号,根据不同种类的隶属度区别实施数据模糊化处置并获取训练样本数据。训练网络和测试数据分别用所得训练样本数据中的80 %以及20 %。以创建变速器油路故障诊断模型为基础[10],通过模糊集合表示法描述变速器油路故障隶属度,使变速器故障现象和故障原因二者合一,概括4 种故障现象以及2 种重要故障原因分别用表1 和表2 描述。

表1 故障现象表

表2 故障原因表
那么根据公式(6)和公式(7)确定故障原因模糊集合Ni以及故障现象模糊集合Mi:
Uyi和Uxi分别是和该故障原因之间的隶属度以及和该故障现象之间的隶属度。
故障原因和故障现象二者间的相互关联,即模糊准则。通过模糊理论中的“if-then”规定处理故障原因和故障现象之间的关联[11],这个“if-then”规定是“if α and β,then γ ”,变量用α 和β 表示,α 和β 协同配合下的效果用γ 表示。表3 为故障现象 M1~ M4和故障原因 N1~N2的关联信息。
隶属度函数的形态大致有矩形遍布、正态遍布以及梯形遍布等,结合本文分析,变速器油路故障隶属度函数是梯形遍布形态[12]。下文是详细步骤:变速器液压系统中油路压强是(1.08~1.47)MPa,最小压强和最大压强分别是1.08 MPa 以及1.47 MPa,因此将(0.0~1.47)MPa 设定成变速器油路故障,用x 和A 分别表示油路压强参量及变速器油路压强过低模糊集合。通过公式(8)获得变速器油路故障隶属函数 A ( x ):
B 代表变速器油路故障模糊集合,此集合包含变速器油路压强过大、油路压强过低等[13],通过公式(9)获得变速器油路压强变化程度 Δn 。
变速器先后2 次收集的油路压强数据分别用 ni和ni+1描述。
公式(10)为变速器油路压强变化程度隶属函数B(x):
综上,获取变速器故障为(0.0~1.0),设置变速器故障的3 个级别,分别是强(0.7~1.0)、中(0.4~0.6)以及弱(0.0~0.3)。从训练得出的样本数据抽取80 %作训练数据并被训练过程中对神经网络各节点的权值更新所用[14],试验、检验模型效果使用余下训练样本数据的20 %。
2 仿真测试与分析
以使用097 自动型变速器的某品牌电动汽车作为本次试验对象。变速器结构包括液压变矩器、齿轮结构、液压系统及驱动控制系统等。图2 为097 型自动变速器外貌。

图2 097 型自动变速器
为验证本文方法下变速器油路故障诊断模型输出结果真实性。将采集到的该电动汽车变速器的100 组故障样本数据随机分成20 份,2 份作为测试样本,18 份为训练样本,本文方法模型输入变量是变速器故障现象,输出变量是变速器故障原因。表4~6 分别表示本文方法模型的测试样本输入、希望样本输出结果以及实际输出结果。以表4 数据为模型输入,通过对表5 和表6 分析可知,本文方法的变速器故障检测结果与希望输出结果基本吻合,更加接近真实情况,可实现电动汽车变速器故障的正确检测。
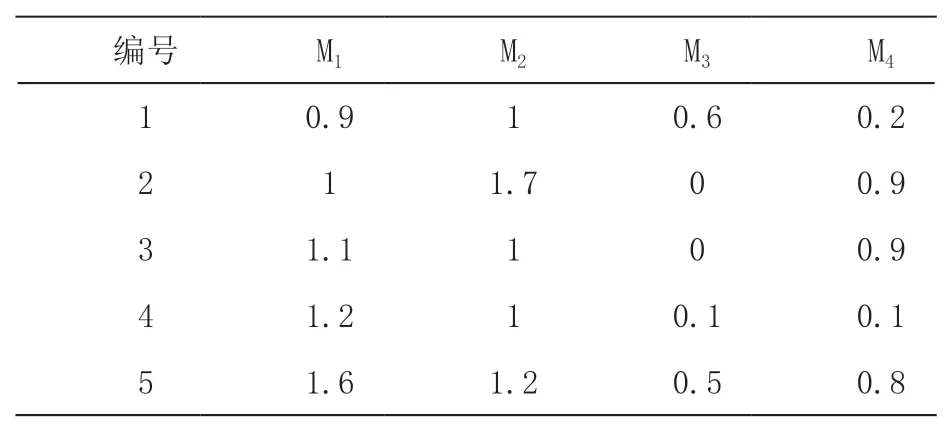
表4 模型测试样本输入
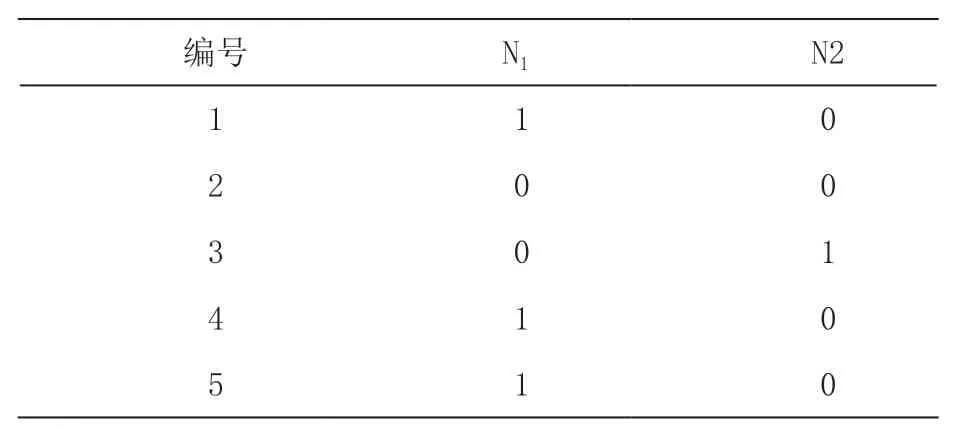
表5 模型希望样本输出结果
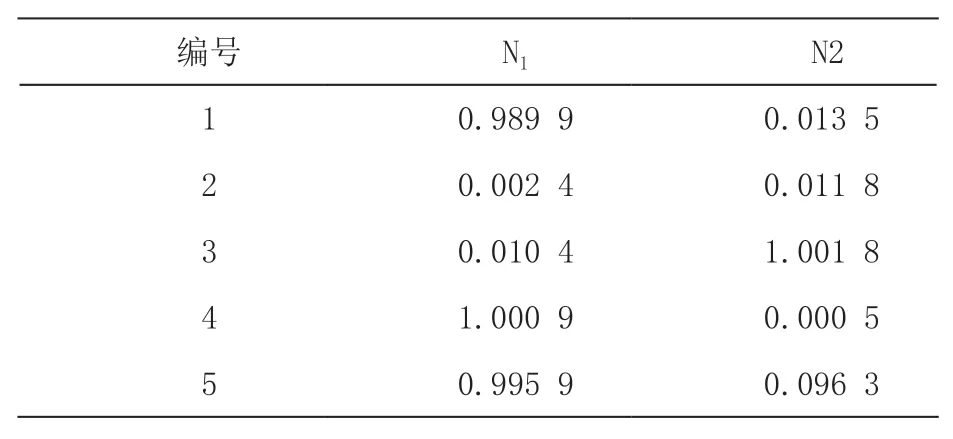
表6 模型实际输出结果
为验证本文方法的变速器故障诊断效果,选取文献[1]结合LMD 与BP 神经网络的故障检测方法和文献[2]基于特征提取的故障检测方法为对比,测试三种方法在电动汽车处于不同运行工况下的故障的检测准确率,结果用表7 表示。分析表7 可知,不同工况下本文方法的故障检测准确率均比文献[1]和文献[2]均高,其重要因素离不开本文方法在建立模型进程中使用已设定好的输入参量。结果说明,本文方法的故障检测准确率较高,且适用于多种电动汽车运行工况下的变速器故障检测。

表7 三种方法的故障检测准确率对比(%)
在BP 神经网络中,隐含层神经元数目极其重要,通常隐含层神经元数目过多或过少都会影响BP 神经网络输出结果。为证实本文方法中隐含层神经元数目对BP神经网络输出结果的重要性,对同一组训练样本取不同的隐含层神经节点数,通过修改学习率算法,训练目标设为10-5,分别对BP 神经网络训练2 000 次,隐含层不同数目的神经元训练误差结果用图3描述。分析图3可知,隐含层神经元数是12时,BP神经网络训练误差结果最小,因此本文方法用12 作为变速器油路故障诊断模型隐含层神经元数目,此刻对电动汽车变速器的故障检测效果最好。
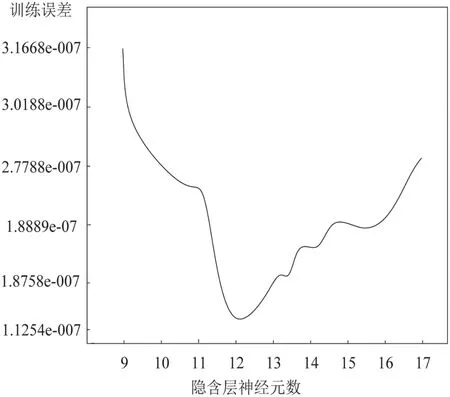
图3 隐含层不同数目神经元训练误差结果
实验给出本文方法应用前后变速器的寿命对比,如图4 所示。分析图4 可知,本文方法应用下的变速器寿命退化情况显著优于未使用本文方法变速器寿命退化情况,可见,应用本文方法进行及时的变速器故障诊断,对延缓汽车变速器使用寿命退化情况具有显著作用。
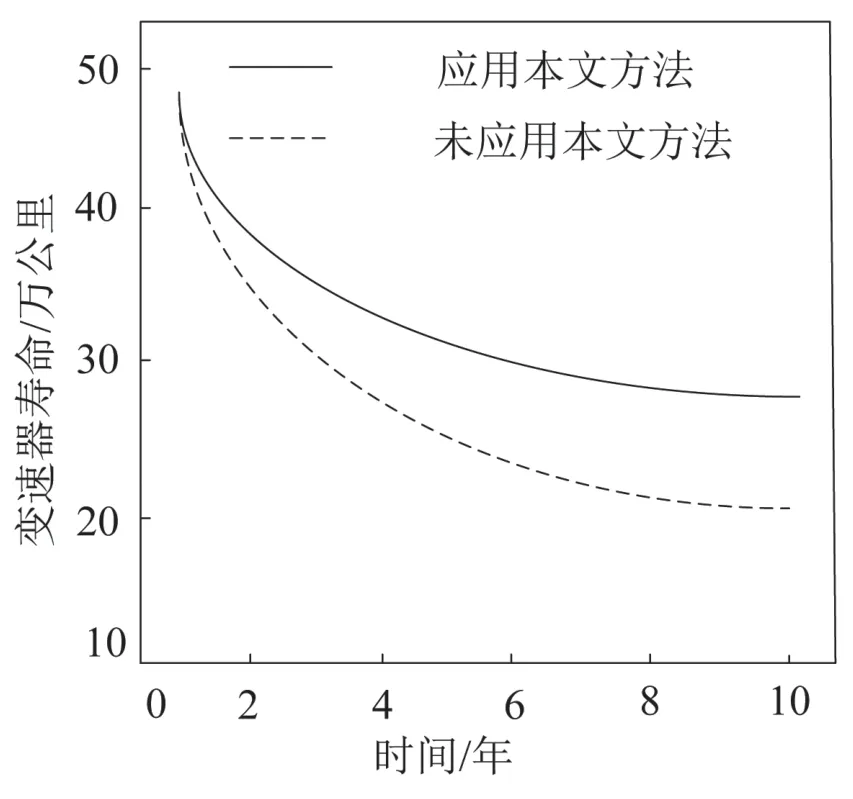
图4 本文方法应用前后变速器的寿命
3 结论
本文使用模糊神经网络对电动汽车变速器进行故障检测,在确定隐含层神经元的数量前提下,不仅可以大幅度提高电动汽车变速器的故障检测正确率,还可延缓电动汽车变速器的使用寿命退化,提升其实际应用性能。希望本文方法在未来可以具备更高的使用价值。
