基于蒙特卡罗的多连杆伺服机械装置性能优化设计

汪晔

（东莞市南博职业技术学校，东莞 523000）

引言

随着大量新技术的应用，多连杆伺服机械装置性能逐渐得到优化，机械装置设备整合度增加，机械装置系统容错度降低。一方面，机械装置设备中的高、低、中压侧设备大幅度增加，内部复杂度增加，另一方面，机械装置设计复杂度伴随着三集五大思想，设备运行环境复杂度的增加速度逐年加快。在高复杂度环境中，传统的可靠性评估模型的自身可靠性降低，所以，研究一种更能适合高复杂度评估环境的伺服机械装置可靠性评估环境成为当前的技术升级需求。李广儒（2021）等针对机械装置系统设计了一套自动化可靠性评估系统，以期达到一定自身可靠性的装置设计可靠性评估系统[1]。徐天寒（2021）等使用Markov 对机械装置系统的间隔层和过程层进行可靠性评估[2]。苗兴园（2020）使用全寿命周期成本管理模型对多连杆伺服机械装置的性能进行了可靠性评估[3]。

蒙特卡罗模型（MCS）是一种基于随机抽样的概率描述模型，可以用于评估复杂度较高的系统可靠性。吕炜枫（2020）等研究了一种基于蒙特卡罗的伺服机械装置性能可靠性分析方案[4]。王丽燕（2020）研究了一种使用蒙特卡罗的伺服机械装置性能的评估方案[5]。

相关文献进行机械装置性能可靠性评估中，均主要针对机械装置的特定子系统或特定逻辑层进行评估，以期降低评估过程的高复杂度带来的数据混沌。该研究核心创新点是将蒙特卡罗模拟算法应用到多连杆伺服机械装置的性能评估中，有利于提升多连杆伺服机械装置性能评估的条理性，属于认知性人工智能的技术范畴，将改变以往通过通用人工智能系统的评价精度较低的问题。本文重点解决多连杆伺服机械装置整体评估的评估方法和性能优化方法。

1 蒙特卡罗模型的核心算法架构

使用蒙特卡罗模型对多连杆伺服机械装置可能发生的故障可能性进行分解，而非通过对多连杆伺服机械装置结构和逻辑拓扑进行分解的方式获得多连杆伺服机械装置的可能故障。即对多连杆伺服机械装置来说，主要的故障来自于多连杆机械设备的运行故障，这也是其故障的主要类型。

如果采用全仿真模拟的方式获取多连杆伺服机械装置故障的仿真过程，在高复杂度的机械架构下，其可靠性评估过程本身可靠性存疑。故采用随机取样法支持的蒙特卡罗模型在Python 平台的支持下进行机械装置故障仿真模拟，以直接针对故障概率统计本身对系统进行故障模拟，以获得系统可靠性，是当前评估过程本身可靠性的有效保障。采用蒙特卡罗算法构建模型，对多连杆伺服机械装置的故障进行计算，其计算流程如图1 所示。

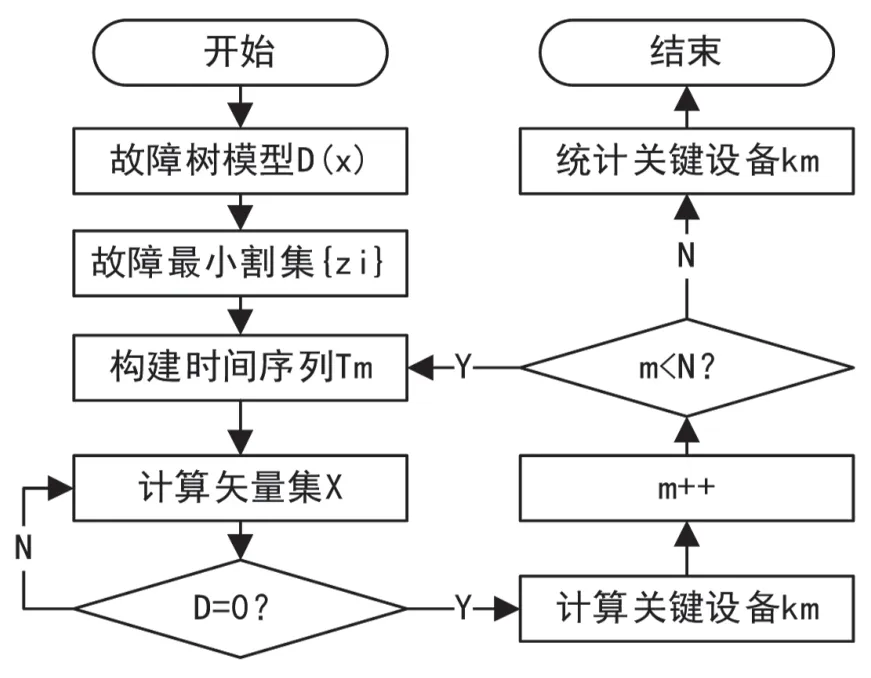
图1 蒙特卡罗模型核心算法示意图

图1 中，为了评估多连杆伺服机械装置结构的性能，对多连杆伺服机械装置的故障进行分析，采取蒙特卡罗算法构建的模型进行装置的故障模拟。①构建多连杆伺服机械装置的蒙特卡罗算法进行故障模拟，基于总仿真次数N，初始化状态下m=0，其结构函数为D（x）；②将蒙特卡罗算法的所有割集求出，构建最小割集集合{zi}；③随机抽样原则下构建蒙特卡罗模型，自变量为仿真过程的时间线变量，随机抽样后沿升序排列，构成时间序列Tm；④限定tj=r′j，每个蒙特卡罗算法最小割集{zi}中的状态向量集，构建算法函数下的状态向量集支持的蒙特卡罗模型D（→），当D=0 时，迭代下一个循环，否则执行下一步；⑤在时间线自变量控制下统计D 值，对系统内失效关键设备Fk ∶rk 进行统计，当m+1＜N 时回滚至第3 步执行，否则汇总仿真结果并输出。

2 多连杆伺服机械装置的蒙特卡罗模型建立

2.1 蒙特卡罗模型的构建

根据前文分析，针对多连杆伺服机械装置的连杆设计，可以建立如下的蒙特卡罗模型：

其中：

F（h）—多连杆伺服机械装置的连杆设计函数；

F（m）—机械装置的故障函数；

F（l）—多连杆连接设备的故障函数；

在此模型上以多连杆伺服机械装置的连杆设计函数为例，还牵扯到机械装置的故障和多连杆连接设备的故障，即：

其中：

AI( x ), BI( x), CI( x)—机械装置的故障函数；

AII( x ), BII( x), CII( x)—多连杆连接设备的故障函数。

针对机械装置的故障、多连杆连接设备的故障函数的分解方法，同样可以根据分段和各连接机构故障进行相应分解。

根据多连杆伺服机械装置的运行数据，设定对应连杆连接设备的平均无故障运行时间为TMTTF，平均故障修复时间为TMTTR，对此两变量进行统计分析，可以得到系统的运行时间和修复时间的分布图，得到其概率分布函数F（x）：

对其运行状态进行数值量化分析，当其正常运行时，设定F=1，当其处于故障状态时，设定F=0，通过观察F值判定多连杆伺服机械装置运行的稳定性。

2.2 数据仿真过程

使用蒙特卡罗模拟法对多连杆伺服机械装置进行性能指标计算和可靠性评估，仿真平台为Python，其具体仿真流程如下：

1）将历史数据进行同构化及归一化处理，构建分析原始数据库；

2）确定模拟的时间周期和模拟步长；

3）根据蒙特卡罗模型，系统初始化并进行数据模拟仿真，统计仿真过程中的多连杆伺服机械装置故障率和连杆运行状态恢复时间周期；

4）根据仿真结果绘制F-T 图和Q-T 图；

5）根据F-T 结果和Q-T 结果对多连杆伺服机械装置的性能做出评估；

对多连杆伺服机械装置的分析时间周期为3 年26 280 h，统计装置平均无故障时间和故障率，得到表1。

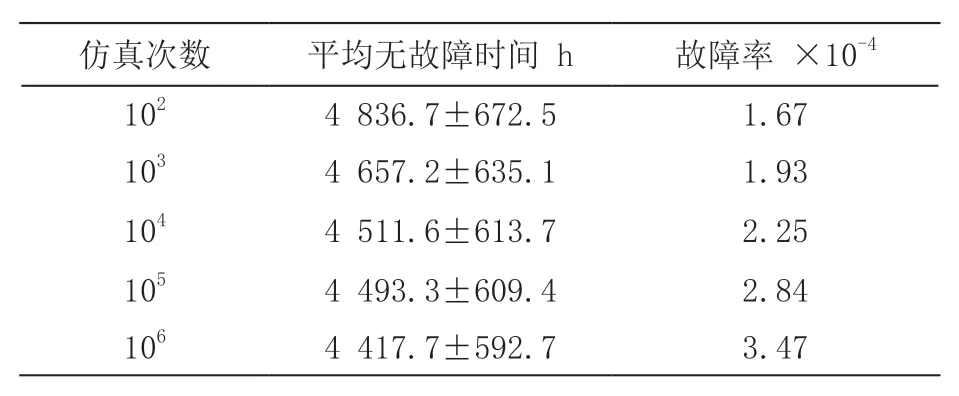
表1 不同仿真次数下的仿真结果对比表

如表1，随着仿真次数从102 次到106 次，平均无故障时间从4 836.7 h 向4 417.7 h 收敛，而装置运行系统故障率从1.67×10-4向3.47×10-4收敛，可见为提升仿真的效率，提升仿真次数可以获得自身可靠性更高的评估。

本文多连杆伺服机械装置系统的平均无故障时间小于（4 417.7±592.7）h，而故障率大于3.47×10-4，使用相同方式对连杆连接机构进行仿真分析，仿真次数为106，结果详见表2。

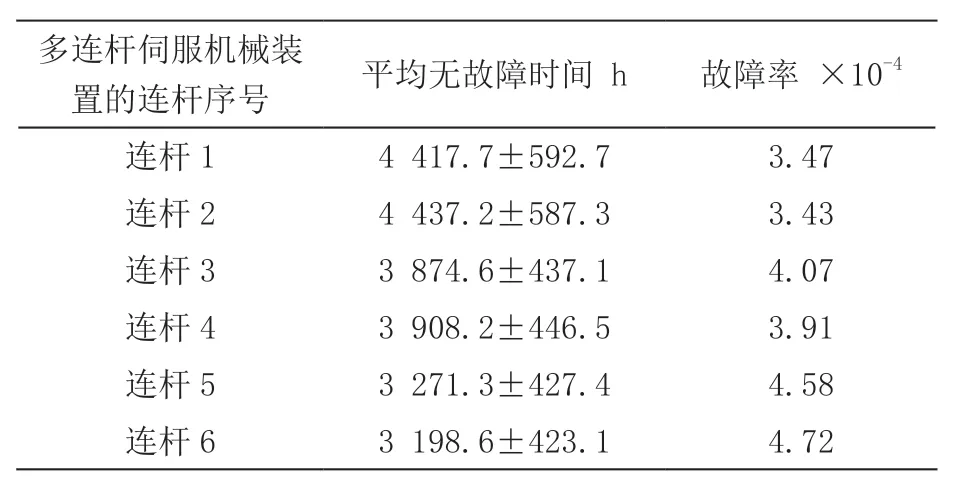
表2 考察连杆连接机构的F-T 分析结果表

根据多连杆伺服机械装置系统安全的木桶法则，系统中最薄弱环节决定了系统的可靠性，且连杆1 和连杆2 的故障大概率导致这两段连杆相互连接机构的故障，所以故障率最高的连杆6 的F-T 结果，可以确定多连杆伺服机械装置系统的可靠性。

使用蒙特卡罗模拟法对时间周期上的Q-T 图进行绘制，如图2。

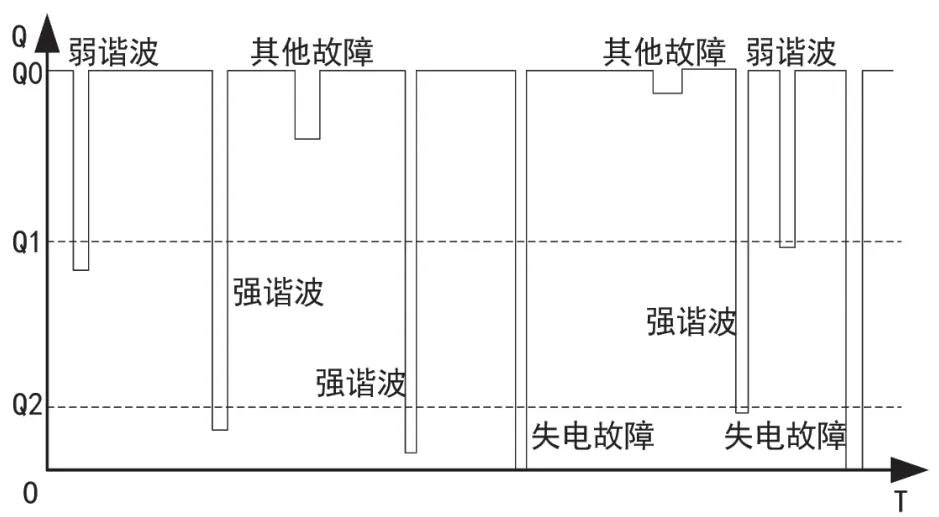
图2 Q-T 分析结果局部

图2 中，当系统Q 值运行在Q0 级别上时，认为多连杆伺服机械装置系统系统处于正常运行状态，而当Q＜Q2 时，认为系统发生了强谐波故障，当Q=0 时，认为装置系统发生了失电故障，当系统运行在Q1＜Q＜Q2 时，认为系统发生了弱谐波故障，当系统运行在Q0＜Q＜Q1 时，认为系统发生了其他故障。

使用该方法对多连杆伺服机械装置3 年内6 段连杆的实际运行状态进行分析，其结果如表3。

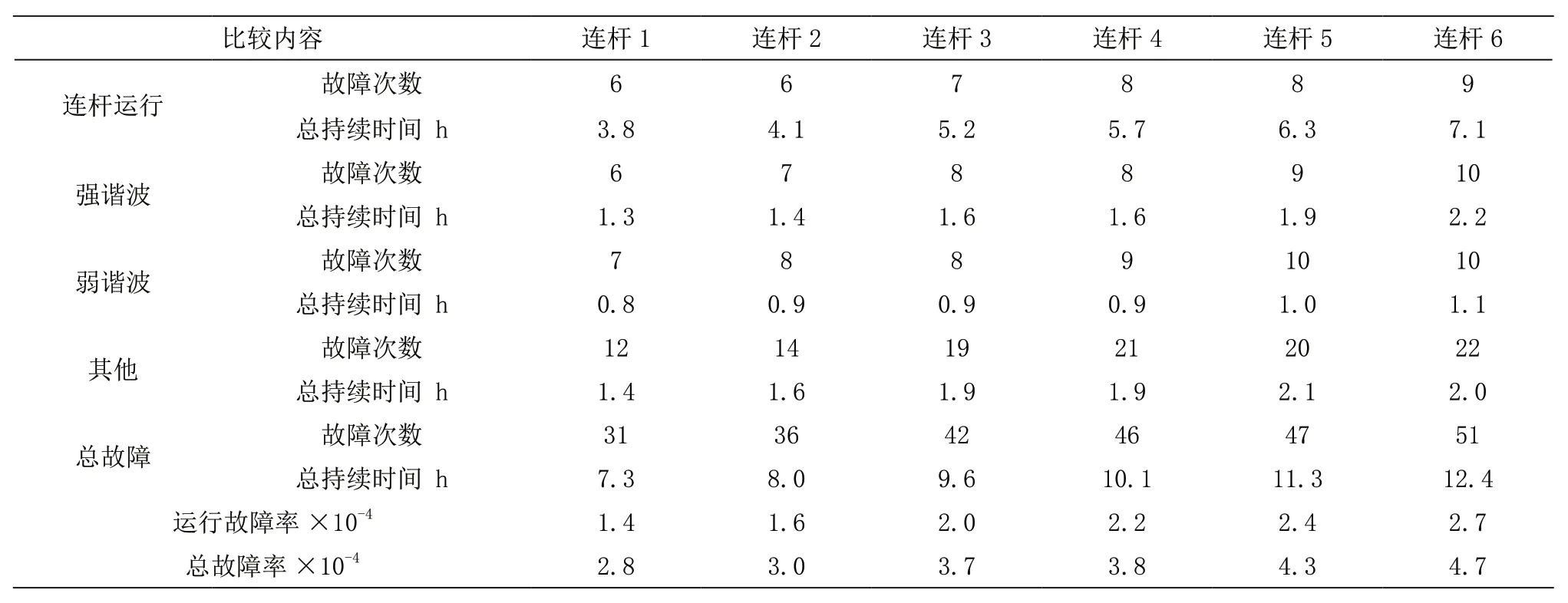
表3 考察多连杆伺服机械装置连杆的Q-T 分析结果

2.3 基于蒙特卡罗模型的多连杆伺服机械装置性能的可靠性评估

对上述多连杆伺服机械装置运行过程中的两个故障率分析结果进行汇总，可得表4。

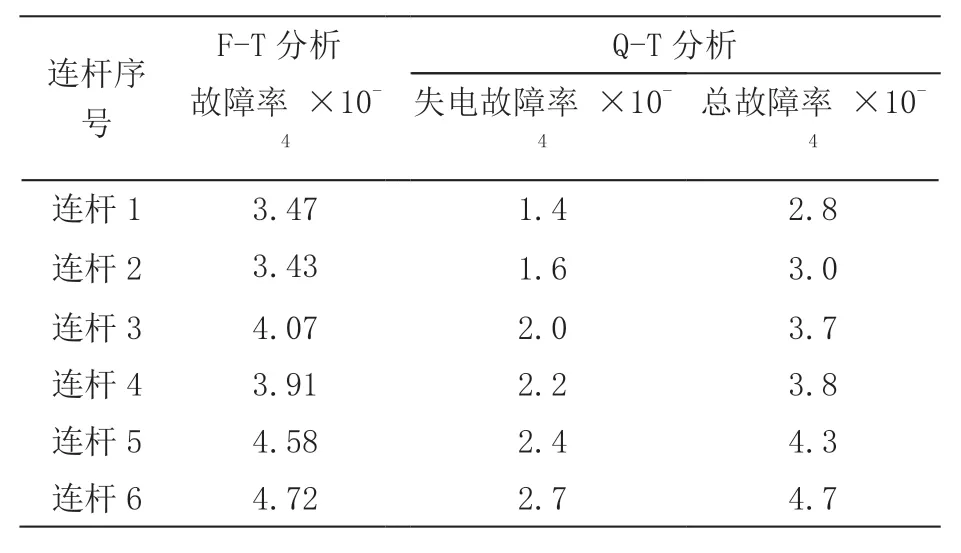
表4 多连杆伺服机械装置运行故障率分析结果汇总表

从表4 中可以看到，F-T 分析的故障率分析结果与Q-T 分析中的总故障率分析结果较为接近，而Q-T 分析中的失电故障率分析结果远小于另两者。单纯性在上述结果中选择某一项故障率分析结果对系统可靠性做出评估，评估过程的自身可靠性存疑。故采用加权指标法对其进行汇总。

即：

其中：

A1—F-T 分析的故障率传导的可靠性评估；

A2—Q-T 分析的连杆结构故障率传导的可靠性评估；

A3—Q-T 分析的总故障率传导的可靠性评估。

根据不同连杆运行可靠性对多连杆伺服机械装置系统可靠性的影响，将上述6 个连杆的评估结果进行加权分析，可得：

将上述6 个连杆机构分为三段，式中：

Ah1, Ah2—第一段连杆的可靠性，即连杆1 和连杆2的可靠性；

Am1, Am2false 分别为第二段连杆的可靠性，即连杆3 和连杆4 的可靠性；

Al1, Al2false 分别为第三段连杆的可靠性，即连杆5 和连杆6 的可靠性；

结合公式（3），故障率向可靠性的传导函数可写做：

各连杆可靠性因子可传导为表5。

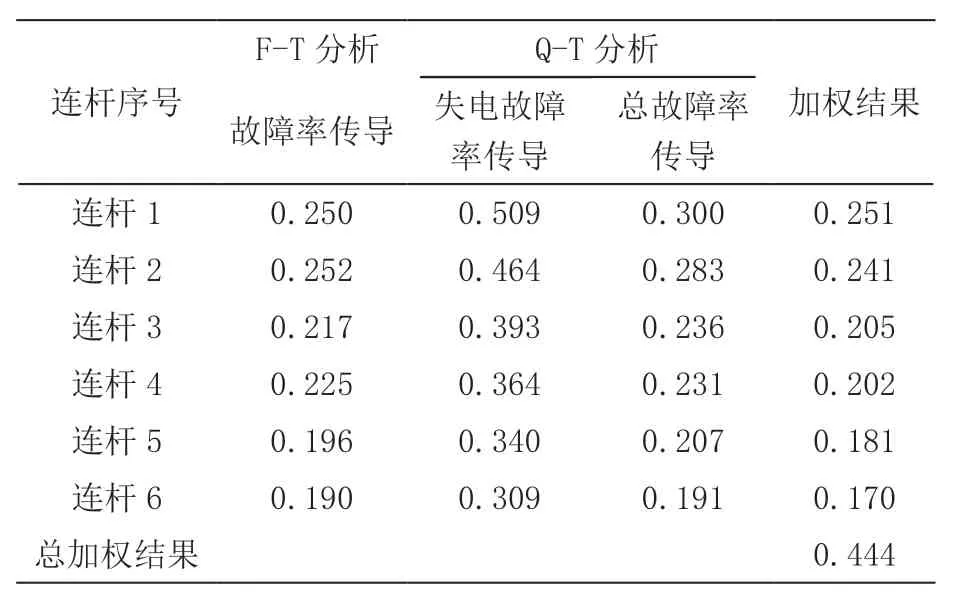
表5 连杆可靠性因子传导结果表

3 多连杆伺服机械装置性能可靠性评估结果的意义

本文是在蒙特卡罗模型下的可靠性评估结果，属于对多连杆伺服机械装置故障率分析结果的负倒数幂投影，属于中深度挖掘数据结果，且不同连杆架构下的综合评估结果因为连杆结构层次和加权权重分配方式的不同各有不同。所以，其本身对反应多连杆伺服机械装置性能的可靠性无统计学意义，且不同机械装置之间无法通过比较其可靠性结果得到不同机械装置的可靠性差异，但其变化趋势对多连杆伺服机械装置性能可靠性评估有积极意义。即在移动时间窗口下，当该评估结果上升时，多连杆伺服机械装置的综合故障率下降，反之，多连杆伺服机械装置的综合故障率上升。

所以，构建多连杆伺服机械装置在一定周期的移动分析窗口，即在分析当前数据时，向后选取一定周期的分析数据，如90 天～180 天数据，根据该数据动态计算多连杆伺服机械装置性能的可靠性评估结果，其分析结果如图3。

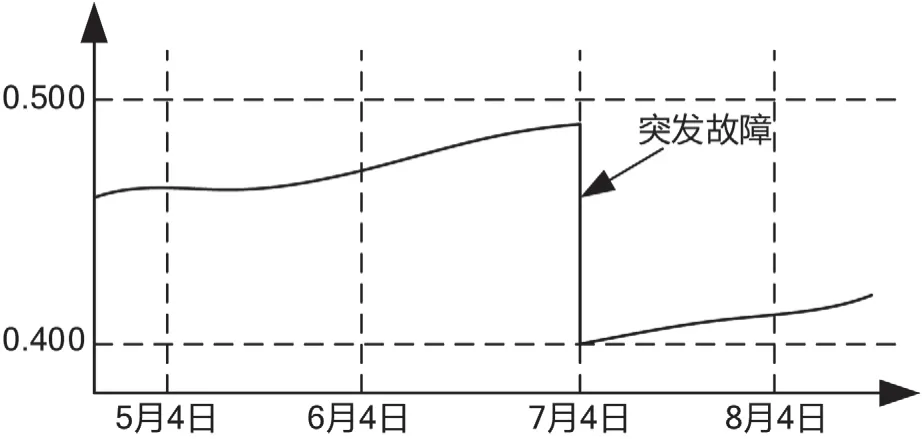
图3 移动窗口下的可靠性评估结果示意图

图3 中，由于该多连杆伺服机械装置在运行的过程中突发机械故障，故障影响时间为47 min（0.783 h），所以导致该多连杆伺服机械装置可靠性评估结果从0.492陡跌至0.403，但因为算法影响，多连杆伺服机械装置无故障运行时间增加的过程会导致该装置可靠性评估结果累积上升。即2019 年5 月4 日评估结果为0.469 而至2019 年7 月4 日故障发生前沿上升至0.492，事故发生后，该评估结果下跌至0.403 而至2019 年8 月4 日，该评级结果恢复至0.416，评估结果中可以看出多连杆伺服机械装置的运行状态和性能，根据相应的数据进行机械装置的性能优化。

4 总结

基于蒙特卡罗模型的多连杆伺服机械装置性能优化设计，根据上述多连杆伺服机械装置可靠性分析结果，与装置系统的故障发生周期负相关，与故障影响范围负相关，与无故障运行时间正相关。随着系统无故障运行时间持续增长，系统的可靠性评估结果也在移动窗口中持续增长，当多连杆伺服机械装置小规模故障发生时，将影响该可靠性评估结果的增长过程，当大规模故障发生时，会导致该评估结果陡降。所以该评估结果对多连杆伺服机械装置的性能优化和可靠性设计有一定的敏感性。