半正弦波冲击试验的测量不确定度评定
2023-05-28胡凯翦文斌张旺威张仕彬
胡凯,翦文斌,张旺威,张仕彬
(威凯检测技术有限公司,广州 510663)
引言
半正弦波冲击试验往往是电工电子可靠性验证阶段中常见的力学试验,用于考核产品结构在实际使用、运输过程中受到来自路面或其他外力对自身的冲击。其测量结果的可信程度也非常重要。本文结合GB/T 27418 和JJG 1174 的两个标准,就加速度幅值、脉宽持续时间、速度变化量这三个重要参数,针对半正弦波冲击试验进行测量不确定度评定,以确定冲击试验测量结果的可信程度。这种附有测量不确定度的冲击试验结果才是完整的、也是试验结果合理度、满意度的重点。
1 半正弦波冲击试验的参数测量方法及建模
测量方法如图1 所示,用PULSE 分析系统、数字多用表、单相压电加速计和三相压电加速度计作标准,在台面中心点布置传感器对所需要的参数采用直接法进行测量。并对加速度、脉宽持续时间、速度变化量参数,建立数学模型。加速度的数学模型公式为:
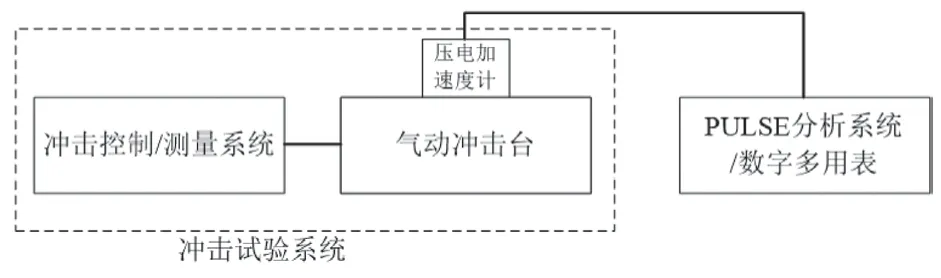
图1 冲击试验参数测量原理图
式中:
A—PULSE 分析系统的实际值;
A1—冲击台的示值;
A2—冲击台的修正值;
A、A1、A2的单位均为g。
建立脉宽持续时间的数学模型公式为:
式中:
T—PULSE 分析系统的实际值;
T1—冲击台的示值;
T2—冲击台的修正值;
T、T1、T2的单位均为ms。
2 半正弦波冲击试验的不确定度来源和分类
对不确定度的分析应列举不确定度的来源,确定对试验结果影响的因素。因此,半正弦波冲击试验不确定度的来源可能是对被测量参数定义的不完善、对测量结果受外界因素影响的识别不充分、设备的分辨率或取样代表性不够等。最后,需要对不确定度的来源进行准确地分类。
另外,半正弦波冲击试验的不确定度也包括A 类和B 类标准不确定度。A 类标准不确定度一般是对观测数据进行统计分析而进行评定的标准不确定度,其一般以贝塞尔公式进行计算;B 类标准不确定度是通过非统计分析方法得出的不确定度分量,一般包括试验设备的误差、校准证书提供的数据、设备说明书、设备特性等,但B 类不确定度需要转化为B 类标准不确定度。
冲击试验的试验参数可以先参考计量校准标准JJG 1174-2021 对冲击设备的某个参数进行数据采集。考虑到冲击台也类似于振动台,其台面的材质、台面尺寸和刚度都会对均匀度产生影响。而且,不同的冲击试验设备使用的波形发生器尽有不同,例如羊毛毡或橡胶,随着冲击次数的增加其加速度和脉宽持续时间也会改变。因此,本文冲击台的参数建模、设备的自身特性、数据采集方法、测量仪器的参数等,列举所有影响评定结果的不确定度来源并对其进行分类和量化。
2.1 半正弦波冲击试验的A 类不确定度分量
人员测量重复性引入的标准不确定度,即冲击台的加速度平均值引入的标准不确定度分量u1、脉宽持续时间平均值引入的标准不确定度分量u2;冲击台面响应特性引入的标准不确定度,即冲击台不同测量位置、不同测量时间的加速度差引入的标准不确定度分量u3、冲击台在不同测量位置、不同测量时间的脉宽持续时间差引入的标准不确定度分量u4都属于A 类标准不确定度。计算公式如下:
(1)冲击加速度平均值引入的标准不确定度分量u1,公式为:
式中:
Amn—第m个测量点的第n 次读数;
x —台面的测量点个数;
y—每个测量点的读数次数。
2)脉宽持续时间平均值引入的标准不确定度分量u2(即计算所有测量点的标准差),公式为:
式中:
Tmn—第m 个测量点的第n 次读数;
x —台面的测量点个数;
y—每个测量点的读数次数。
3)冲击台在不同测量位置、不同测量时间的加速度差引入的标准不确定度分量u3(即抽取具有代表性的测量点计算其标准差),公式为:
式中:
Acd—第c 个测量点的第d 次读数;
a—冲击台上的代表性测量点个数;
b—冲击台上的代表性测量点的读数次数。
4)冲击台在不同测量位置、不同测量时间的脉宽持续时间差引入的标准不确定度分量u4(即抽取具有代表性的测量点计算其标准差),公式为:
式中:
Tcd——第c 个测量点的第d 次读数;
a—冲击台上的代表性测量点个数;
b—冲击台上的代表性测量点的读数次数。
2.2 半正弦波冲击试验的B 类不确定度分量
压电加速计的准确度等级引入的标准不确定度分量u5、标准电荷放大器的允许误差引入的标准不确定度分量u6、PULSE 分析系统的允许误差引入的标准不确定度分量u7、冲击台横向运动比引入的标准不确定度分量u8都属于B 类标准不确定度。计算公式如下:
1)压电加速计的准确度等级引入的标准不确定度分量u5,可以根据压电加速计的准确度等级进行计算,公式为:
式中:
Z—压电加速度计的准确度;
k —置信系数[1]。
2)标准电荷放大器的允许误差引入的标准不确定度分量u6,可以根据标准电荷放大器的允许误差进行计算,公式为:
式中:
W—标准电荷放大器的允许误差;
k —置信系数。
3)PULSE 分析系统的允许误差引入的标准不确定度分量u7,可以根据PULSE 分析系统的允许误差进行计算,公式为:
式中:
Y—PULSE 分析系统的允许误差;
k —置信系数。
4)冲击台的横向运动比引入的标准不确定度分量u8,可以冲击台的横向运动比进行计算,公式为:
式中:
H —冲击台横向运动比;
k —包含因子。
3 半正弦波冲击试验的参数不确定度计算
3.1 半正弦波冲击试验的A 类不确定度计算
半正弦波冲击试验的A 类不确定度,包含人员测量重复性引入的标准不确定度分量u1和u2、冲击台面响应特性引入的标准不确定度u3和u4。利用PULSE 分析系统、数字多用表、单相压电加速计和三相压电加速度计,对冲击台进行数据采样。设定冲击目标条件为15 g/11ms,在冲击台面布置5 个测量点(如图2 所示)。启动设备在5 min 内进行5 次半正弦波冲击试验,每1 min 记录所有的加速度传感器的试验数值一次。
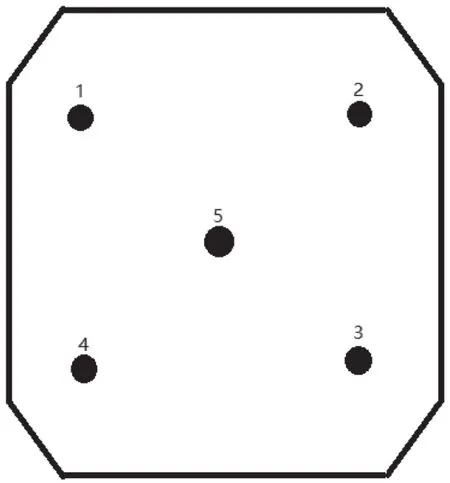
图2 冲击台面的布点示意图
通过PULSE 分析系统进行数据采样,记录的数据如表一所示。根据公式(3)计算表1 的数据得出5 个测量点的25 次加速度数据的平均值为:15.05 g,脉宽持续时间数据的平均值为:10.44 ms。根据公式(5)、公式(6)并选取位置1、位置3、位置5 的5 次测量数据,计算表2 的数据得出冲击台面不同测量点的15 次数据的平均值为:15.09 g,脉宽持续时间数据的平均值为:10.67 ms。因此,根据公式(3)、公式(4)和表1 的数据计算出人员测量重复性引入的标准不确定度分量u1=0.42 g,u2=0.92 ms。根据公式(5)、公式(6)和表1 的数据计算出冲击台面响应特性引入的标准不确定度u3=0.42 g,u4=0.59 ms。
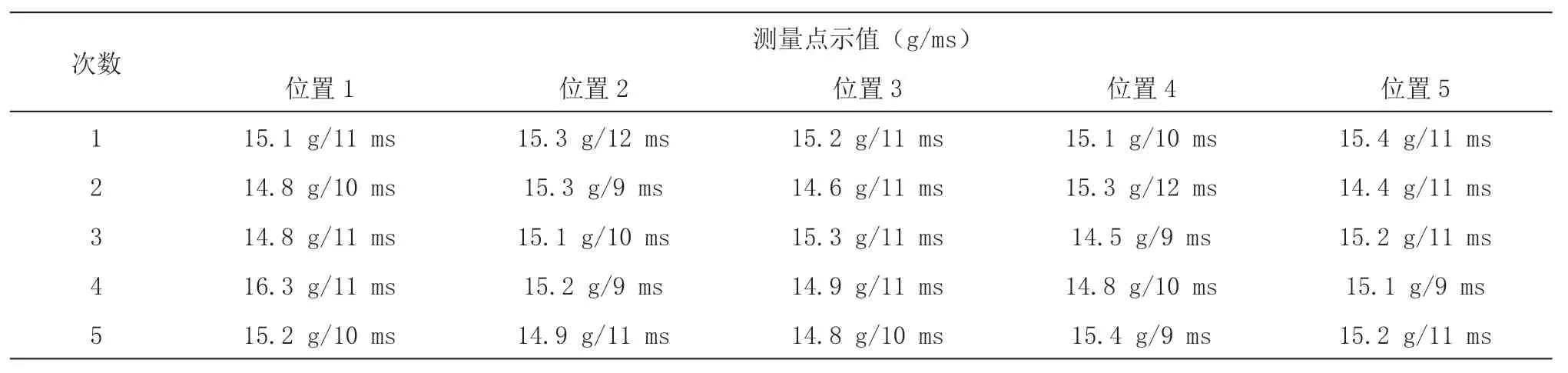
表1 台面各测量点数据
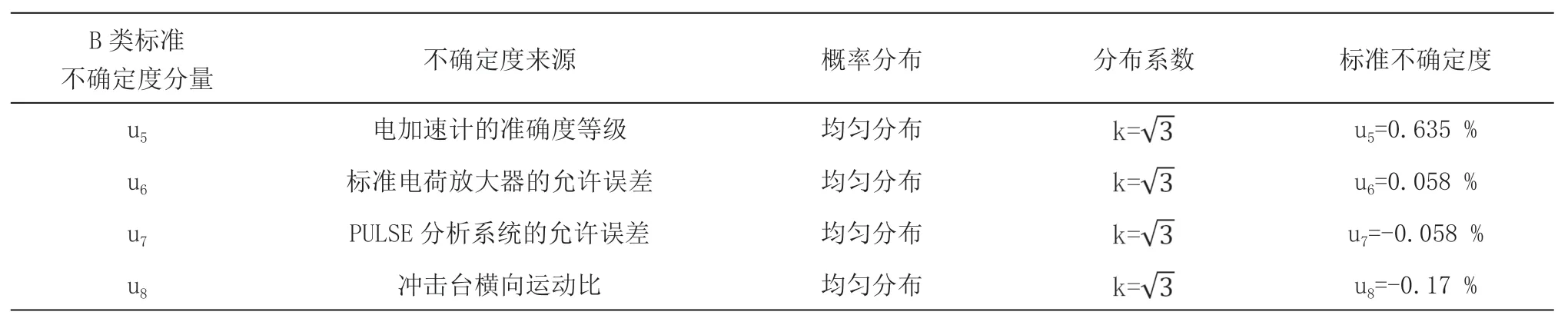
表2 设备特性的B 类标准不确定度分量
3.2 半正弦波冲击试验的B 类不确定度计算
半正弦波冲击试验的B 类不确定度,包含压电加速计的准确度等级引入的不确定度分量u5、标准电荷放大器的允许误差引入的不确定度分量u6、PULSE 分析系统的允许误差引入的不确定度分量u7、冲击台横向运动比引入的不确定度分量u8,根据公式(7)~公式(10)可将其转化为标准不确定度分量,如表2 所示。
3.3 合成标准不确定度和扩展不确定度的评定
4 结语与建议
本文结合标准GB/T 27418、JJG 1174 和冲击试验设备,通过列举实例分析冲击试验中的不确定度来源,并对冲击台的半正弦波冲击实际测量参数进行量化计算,更加直观地观察到冲击试验参数(加速度、脉宽持续时间、速度变化量)的误差范围和置信水平。不可否认,试验结果的测量不确定度评定是一个非常复杂的过程。任何试验的结果都跟试验人员能力和设备性能息息相关。因此,作为试验人员要对试验数据、试验结果时刻保持敏锐感,在试验过程中需要更全面、更细致地考虑、留意影响试验结果的因素,再去分析和确定相应的试验数据的测量不确定度。
