基于自适应虚拟电阻的广域有源阻尼器

李志军，贾 杨，张家安

基于自适应虚拟电阻的广域有源阻尼器

李志军1, 2，贾 杨3，张家安1, 2

(1. 河北工业大学省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2. 河北工业大学河北省电磁场与电器可靠性重点实验室，天津 300130；3. 河北工业大学人工智能与数据科学学院，天津 300130)

并网逆变器是分布式发电系统与电网之间的电能变换接口，然而，随着分布式电源的广泛分布，并网的公共耦合点(point of common coupling，PCC)和电网之间含有较长的输电线路、较多的隔离变压器，导致电网和发电系统之间联络变弱，电网等效阻抗增加，电网呈现弱电网特性. 并网逆变器与电网弱联络时，并网逆变器的锁相环(phase-locked loop，PLL)、电流控制环的控制作用会在较广的频域内引入负阻尼，可能导致系统在广域范围内失稳.为了解决这一问题，本文建立了考虑PLL影响的并网逆变器广域阻抗模型，提出了基于阻抗分析的广域稳定性判据，并在此基础上通过在PCC点并联有源阻尼来稳定系统的方法设计了一个广域有源阻尼器，将其并联连接到PCC点，使其在PCC点合成一个并联阻尼电阻以抑制系统产生的谐振. 当系统工况发生变化时，通过提取PCC点谐振电压并利用谐波含量限制的方法来自适应调节虚拟电阻值，实现广域范围内镇定系统的效果. 最后在MATLAB/ Simulink中搭建了并网逆变器等值系统模型，通过时域仿真验证了该广域有源阻尼器的正确性和有效性.仿真结果表明，并网逆变器与电网弱联络时，PLL、电流控制环控制作用等会引起广域谐振稳定性问题，所设计的广域有源阻尼器能有效抑制广域范围内的谐振，且当系统联络突然发生变化时，也可以有效实现系统的广域镇定.

并网逆变器；锁相环；电流控制环；广域有源阻尼器；广域稳定性

近年来，化石能源的逐渐枯竭和环境污染的日益严重使得发展可再生能源成为必然选择．以电力电子变流器为接口的可再生能源发电单元及设备占比的提升，在一定程度上提升了电网的灵活性、可持续性以及效率，但同时也对电力系统的稳定性和电能质量提出了新的挑战[1]．变流器通常配备宽时间尺度的控制系统，用于调节与电网之间交换的电流和功率[2].变流器的宽时间尺度动态控制可导致与电机的机电动态和与电网的电磁暂态之间的交叉耦合，可能使系统在很宽的频率范围内产生谐振问题[3]．

电流控制环在变流器的稳定性评估中起着很重要的作用，变流器的快速内部电流环与无源器件之间的相互作用可能会导致高频谐振[4]，变流器数字控制系统的时间延迟[5]、开关调制和采样过程的频率耦合机制[6]也会激发高频谐振．文献[7]分析得出逆变器电流控制环与电网阻抗之间的相互作用会产生几百赫兹甚至几千赫兹的高频谐振．一些研究也表明了变流器的外部功率控制和PLL对系统稳定性的负面影响，文献[8]建立了变流器的数学模型，分析指出变流器的恒功率控制会在低频段引入负阻尼，导致低频谐振．文献[9]建立了带PLL的单相并网逆变器阻抗模型，详细分析了PLL带宽、功率因数角、电流参考幅值对系统稳定性的影响．文献[10]分析指出PLL的存在降低了逆变器输出阻抗的幅值与相角，导致系统相位裕度大幅减小，并网逆变器稳定性降低．文献[11]对带PLL的并网逆变器进行了研究，结果表明弱电网下采用动态响应速度较快的PLL易导致并网逆变器出现100～800Hz的中频谐振．由此可见，并网逆变器的PLL、电流控制环与电网阻抗之间的相互作用会在中频、高频两个频段内产生稳定性问题，本文将这两个频段的稳定性问题合并在一起进行讨论，将其定义为广域稳定性问题．

并网逆变器与电网弱联络时，电流控制环和PLL的动态响应会引发逆变器输出阻抗和电网阻抗的交互作用，可能导致系统在广域范围内失稳．为了稳定系统，通过调整电流控制器参数[12-13]、PLL参数[14-15]、改进PLL结构[16-17]来对并网逆变器输出阻抗进行重塑．然而，这些方案通常需要改变并网逆变器的内部结构，包括已经被模块化设计好的电源电路和控制算法，这会大大增加开发周期和成本，并带来较大的改造风险．文献[18]结合系统电压通过PLL对电流控制环的影响，提出了一种改进的前馈控制方法来减小PLL的输出影响，能够有效提高并网逆变器与电网弱联络条件下运行的稳定性．文献[19]构建了一种对弱电网表现友好的新型锁相环结构，能够附加必要的惯性与阻尼，对并网逆变器的输出阻抗进行重塑，以提高弱电网下并网逆变器系统的稳定性．但文献[18]和文献[19]都未考虑电流控制环对并网逆变器稳定性的影响．文献[20]提出采用虚拟阻抗的方法对逆变器输出阻抗进行校正，使得逆变器在电网阻抗宽范围变化时仍然能够稳定工作，同时保证并网电流满足谐波标准，但未考虑PLL对逆变器输出阻抗的影响．文献[21]运用了电阻式有源电力滤波器(R-APF)的方法，控制逆变器在非基频下表现为电阻负载，但需要高带宽的电流控制器来覆盖宽频范围内的谐振，若逆变器的采样频率与基频之比较低则很难实现．或者，可以在PCC点并联一个阻尼电阻器，以阻尼并网逆变器和电网之间的谐波谐振．文献[22]提出了一种基于高带宽电力电子变流器的有源阻尼器，该有源阻尼器并联连接到PCC点上，在谐振频率处被控制为可变电阻，但仅考虑了由电流控制器相互作用产生的高频谐振，没有考虑由PLL引入的中频谐振．文献[23]不同于已有的并联有源阻尼器，提出了一种串联有源阻尼器，将其串联连接到PCC点和并网逆变器之间，合成的串联虚拟阻抗可直接有效地修正电网阻抗，但也仅就单一的高频谐振问题进行了讨论．综上可以看出，现有的技术存在单一域的“广域”化问题．

为了解决并网逆变器与电网弱联络时，由PLL和电流控制环引入的广域稳定性问题，本文基于典型三相LCL型并网逆变器系统拓扑及控制方式，首先建立了考虑PLL影响的广域阻抗模型；其次，在该广域阻抗模型的基础上，提出了基于阻抗分析的广域稳定性判据，研究PLL、电流控制环对并网逆变器输出阻抗的影响，以及逆变器输出阻抗和电网阻抗之间的交互作用；再次，在PCC点并联连接一个广域有源阻尼器，通过谐振电压提取以及谐波含量限制的方法来自适应调节虚拟电阻值，以在广域范围内抑制谐振、稳定系统；最后，通过搭建仿真模型验证了广域有源阻尼器对并网逆变器系统广域范围内谐振抑制的有效性和正确性．

1 考虑PLL影响的广域阻抗模型及稳定性判据

并网逆变器与电网弱联络条件下，并网逆变器输出阻抗与电网阻抗间存在一定交互作用，可能导致广域稳定性问题．为消除PLL、电流控制环对并网逆变器系统广域稳定性的消极影响，首先需对考虑PLL影响的逆变器-电网交互系统的谐振机理进行研究．因此，本节建立了考虑PLL影响的广域阻抗模型，提出了基于阻抗分析的广域稳定性判据，根据该判据研究了不同电网阻抗值、PLL与电流控制环对并网逆变器稳定性的影响，为后续广域有源阻尼器的提出提供了基础理论和关键技术原理．

1.1 广域阻抗模型

式中：Kp、Ki分别为比例系数和谐振系数；w0、wc分别为基波角频率和截止频率．

根据图1三相LCL型并网逆变器系统结构，可推导出考虑锁相环的并网逆变器控制系统数学模型如图2所示．图中，PWM为PWM环节比例增益；PLL()为PLL的小信号模型，根据文献[24]，其数学表达式可表示为

式中：p、i分别为锁相环路PI控制器的比例、积分系数；PCC、分别为并网电压幅值和功率因数角．

图2 考虑PLL并网逆变器控制系统数学模型

根据图2可推导出并网电流g()的表达式为

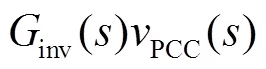
式中()、inv()分别为电流控制环的开环增益和闭环输出导纳，其表达式分别为

式(3)可改写为

式中inv()和PLL()分别为逆变器输出阻抗和PLL等效阻抗，其表达式分别为

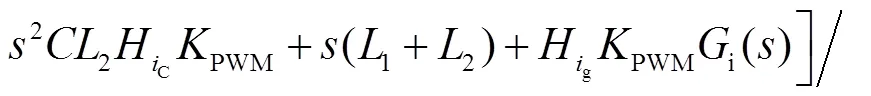
由式(6)可得考虑PLL影响后的并网逆变器输出阻抗为

通过诺顿等效化简图2所示的考虑PLL的并网逆变器控制系统数学模型，可得到图3所示的并网逆变器广域阻抗模型．由式(9)可看出，考虑PLL影响的并网逆变器广域阻抗模型为并联阻抗模型，并网逆变器输出阻抗ZO(s)由逆变器输出阻抗Zinv(s)和PLL引入的负阻抗ZPLL(s)并联构成．该广域阻抗模型不仅能反映电流控制环对逆变器输出阻抗的影响，还能反映PLL对逆变器输出阻抗的影响，可基于该模型分析PLL影响的中频域和电流控制环影响的高频域两个频域的谐振问题．

1.2 基于阻抗分析的广域稳定性判据

利用文献[25]所提出的基于阻抗的稳定性判据可判断弱联络条件下并网系统的稳定性，但该稳定判据未考虑PLL的影响．本文结合文献[25]的稳定性判据与第1.1节所建立的广域阻抗模型，提出了基于阻抗分析的广域稳定性判据，同时考虑了电流控制环与PLL的影响．由图3可得

根据式(10)可知，考虑PLL后系统要实现广域稳定，必须同时满足以下两个条件：①1/O()稳定；②g()/O()满足Nyquist稳定判据．

条件①要求并网逆变器在g()＝0时能稳定运行，1/O()无右半平面极点．由于1/O()＝1/inv()＋1/PLL()，所以只需分别保证1/inv()与1/PLL()不含右半平面极点即可保证1/O()稳定．根据文献[9]分析可知，条件①可进一步表述为确保并网电流闭环与PLL分别稳定．条件②则要求g()和O()的幅频曲线没有交点，或交点处的阻抗比g()/O()具有足够的相位裕量(phase margin，PM).假设g()和O()交点处对应的频率为int，则PM可表示为

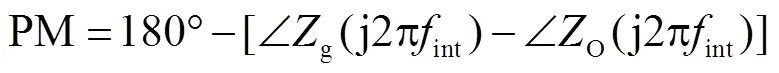
由于电网阻抗g()一般呈阻感特性，且其中的阻性成分有一定阻尼特性，有利于系统的稳定．所以，考虑最坏的情况即将电网阻抗视为纯感性电网阻抗，此时g()＝g，g表示电网的等值电感，其波特图如图4中虚线所示．可以看出，g的变化会使g()的幅频曲线在较宽频率范围内左右平移，可能导致广域稳定性问题．由于g()在所有频率处的相位都为90°，式(11)可简化为

由于电网阻抗可能会在较宽的频率范围内变化，很难保证g()和O()的幅频曲线没有交点．由式(12)可得，O()在交点频率int处的相位应大于-90°才可保证PM＞0．然而，由于PLL、电流控制环等的影响，O()的相位可能在广域范围内低于-90°，交点一旦出现在这些频段，系统将会不稳定，导致广域稳定性问题．

根据表1列出的并网逆变器系统参数，可得到并网逆变器输出阻抗O()的波特图，如图4中实线所示．可以看出，电网阻抗的改变，会使g()和O()的幅频曲线在广域范围内产生交点且交点频率处的相位小于－90°，导致广域范围内的谐振稳定性问题．同时，谐振频率随电网阻抗的增大而逐渐降低，当g取110μH、640μH时，由于电流环控制引入的负阻尼，系统分别会产生2350Hz、1075Hz的高频谐振；当g取1.35mH、4.50mH时，由于PLL的影响，系统分别会产生575.0Hz、177.8Hz的中频谐振．因此，本文提出的基于阻抗分析的广域稳定性判据能有效分析出广域范围内的谐振稳定性问题．

图4 电网阻抗Zg(s)和逆变器输出阻抗ZO(s)的波特图

表1 并网逆变器系统参数

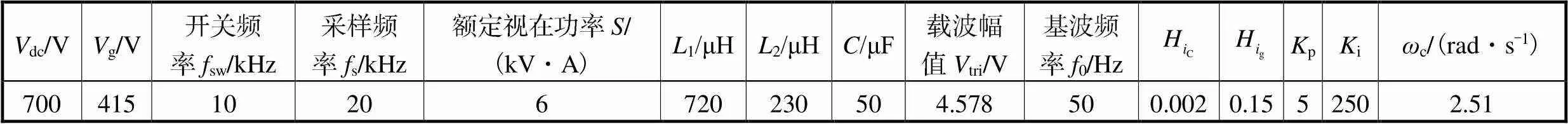
Tab.1 Parameters of grid-connected inverter system

2 广域有源阻尼器的设计

2.1 在PCC点引入有源阻尼来稳定系统

根据第1.2节的阻抗分析表明，电网阻抗g()与逆变器输出阻抗O()交点位置随电网阻抗的增大而降低，交点频率在电流环控制的高频段和PLL控制的中频段都有可能出现．因此，电网阻抗的宽频范围变化可能导致系统出现广域稳定性问题．根据第1.2节提出的基于阻抗分析的广域稳定性判据，为稳定并网逆变器系统，将一个额外的阻抗p并联连接到PCC点来重塑并网逆变器的输出阻抗，提高其相位，如图5所示．

图5 PCC点并联有源阻尼的并网逆变器系统

为了便于分析，将并网逆变器输出阻抗和并联阻抗分别表示为

式中：O()、O()分别为并网逆变器输出阻抗的幅值和相位；p()、p()分别为并联阻抗的幅值和相位．

根据式(13)和式(14)，可以将并网逆变器的输出阻抗和并联阻抗合并在一起，成为新的逆变器输出阻抗，即

2.2 广域有源阻尼器的拓扑结构和控制系统

如图6虚线框中所示为广域有源阻尼器的拓扑结构，由一个三相两电平的电压源型变流器和LCL滤波器构成．将其并联连接到PCC点，以实现广域范围内的谐振抑制．LCL滤波器由滤波电感1A、2A和滤波电容A组成，本文利用文献[26]给出的LCL滤波器参数多目标优化模型进行1A、2A和A参数的选取．dcA、dcA分别为广域有源阻尼器直流侧电容和电压．

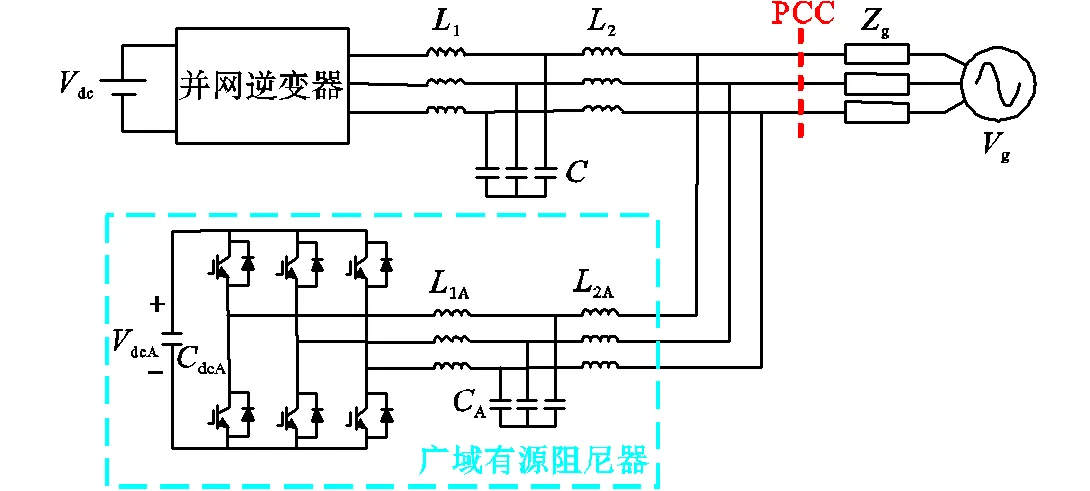
图6 广域有源阻尼器的拓扑结构

式中LPF为截止频率，为了实现波纹抑制和动态响应之间的平衡，选取基频作为截止频率．

图8 虚拟电阻自适应调节算法

若并网逆变器系统是稳定的，则PCCh的值小于lim，系统不需要虚拟电阻，1/V的值为0．一旦系统变得不稳定，在虚拟电阻自适应调节算法的作用下，1/V的值会增大来抑制谐振，使系统稳定．由于电阻调节器RA()可以保证零静态误差，使系统保持在PCCh＝lim的临界稳定状态，1/V也就始终保持为临界值以保证系统在广域范围内稳定．

2.3 广域有源阻尼器的稳定机理分析

为了验证广域有源阻尼器的稳定性效果，需要建立其数学模型进行稳定机理分析．由于广域有源阻尼器外部电压环和锁相环的截止频率通常远低于内部电流环，本文忽略了它们的影响，并将V在稳态时视为常量．根据图7广域有源阻尼器的控制结构，可以得到广域有源阻尼器的简化数学模型，如图9所示．

由图9可以推导出广域有源阻尼器电流控制回路的开环增益和端口电流分别为

图9 广域有源阻尼器的简化数学模型

式中s()、pA()和V()分别为广域有源阻尼器等效基波电流源、原始端口阻抗和虚拟阻抗，表达式分别为

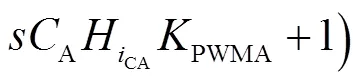
根据式(21)，可以得到广域有源阻尼器的简化等效电路，如图10虚线框中所示．由第2.1节分析可知，如果广域有源阻尼器的原始端口阻抗pA()和虚拟阻抗V()在目标谐振频率范围内均具有正实部，即可稳定系统．表2给出了广域有源阻尼器的具体参数，由于V是实时自适应调节的，分别给出pA()和V()/V的波特图如图11和图12所示．对照图4，可以看出广域有源阻尼器的原始端口阻抗pA()和虚拟阻抗V在中频段和高频段两个频率范围内的相位都在-90o～90o之间，可以有效地使系统在广域范围内稳定．

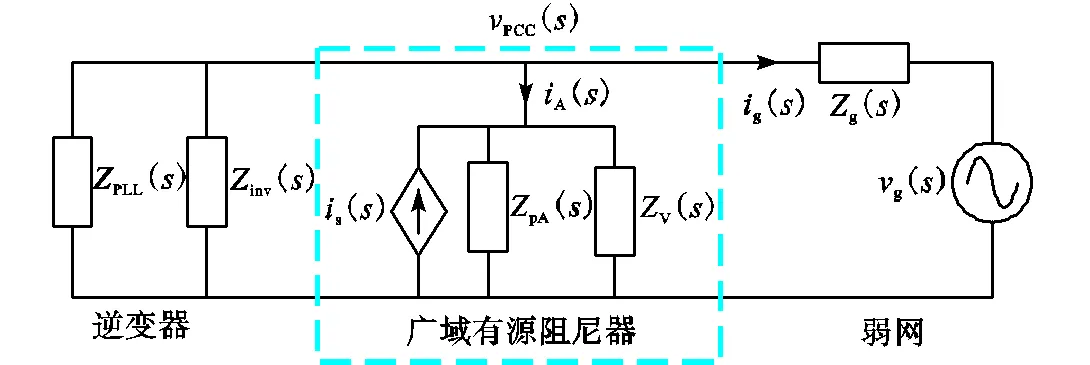
图10 广域有源阻尼器的等效电路

表2 广域有源阻尼器参数

Tab.2 Parameters of the wide-area active damper

图11 原始端口阻抗ZpA(s)的波特图

图12 ZV(s)/RV的波特图

3 仿真验证

为了验证广域有源阻尼器能够有效抑制广域范围内的谐振，根据表1、表2并网逆变器系统和广域有源阻尼器的主要参数，在MATLAB/Simulink中搭建了如图6所示的在PCC点附加广域有源阻尼器后的整体系统模型，分别对广域谐振工况、中高频谐振抑制功能、系统联络突然变化时的广域镇定效果进行仿真验证．

3.1 广域谐振工况仿真

由第1.2节的广域稳定性判据可知，电网阻抗的变化可能会在广域范围内引发谐振稳定性问题，包括PLL引起的中频谐振以及电流环控制引起的高频谐振．分别选取g为4.50mH、1.35mH、640μH、110μH来模拟系统联络的变化进行仿真验证，得到并网逆变器电流谐波频谱如图13所示．可以看出，当g为4.50mH、1.35mH时，由于PLL的影响，并网逆变器系统会产生图13(a)、(b)所示的177.8Hz、575.0Hz的中频谐振；当g为640μH、110μH时，由于电流环的控制作用，并网逆变器系统会产生图13(c)、(d)所示的1075Hz、2350Hz的高频谐振，与图4所示波特图中的谐振频率相对应．因此，并网逆变器与电网弱联络时，电网阻抗宽频范围内的变化会导致并网逆变器系统产生广域稳定性问题．

3.2 中频、高频谐振抑制功能仿真

为了验证所设计的广域有源阻尼器能够有效实现广域镇定，对PLL引起的中频谐振以及电流环控制引起的高频谐振分别进行抑制功能仿真．

当g为1.35mH，由于PLL的影响，系统会出现如图13(b)所示的频率为575Hz的中频谐振．图14为g取1.35mH时并网逆变器PCC点电压和进网电流波形，PCC点电压和进网电流中有明显的中频谐振．在1s时投入广域有源阻尼器，可以看出由PLL引起的中频谐振被有效地抑制住．

将g调大为4.50mH，系统会出现如图13(a)所示的频率为177.8Hz的中频谐振．图15为g取4.50mH时并网逆变器PCC点电压和进网电流波形，谐振频率相比于图14变得更低，但同样为由PLL引起的中频谐振．1s时投入广域有源阻尼器，谐振同样被有效地抑制住了．由此可见，广域有源阻尼器能有效抑制由PLL引起的中频谐振．

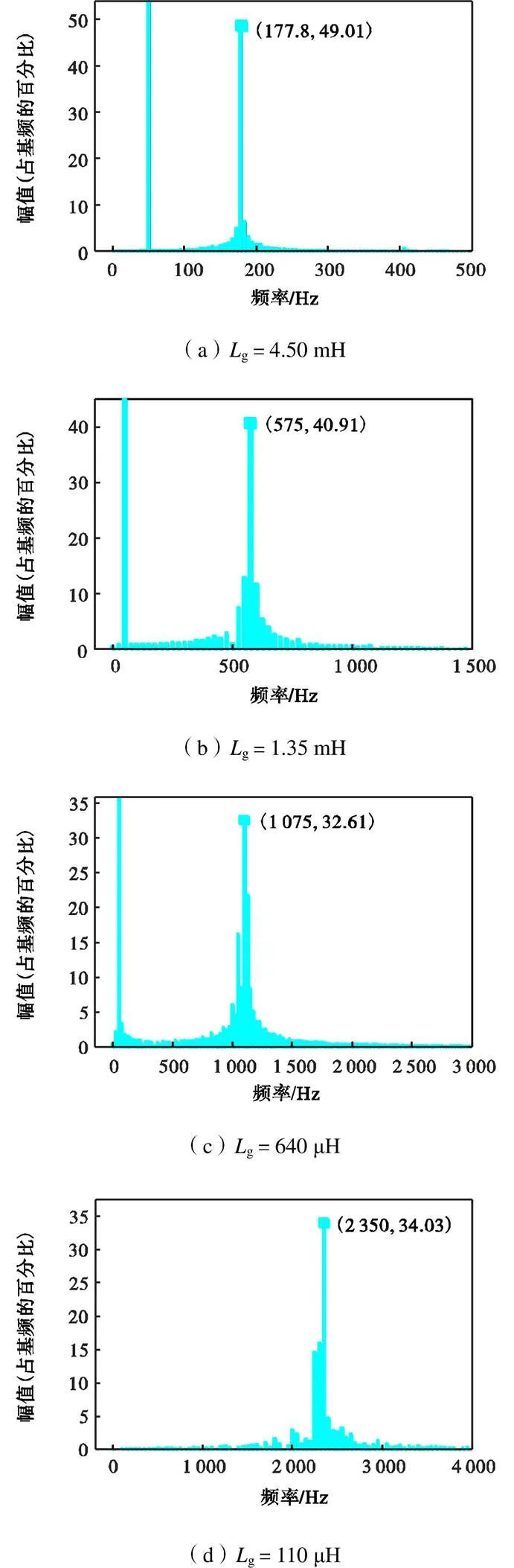
图13 并网逆变器电流谐波频谱(基频(50Hz)＝100%)

图14　　并网逆变器PCC点电压和进网电流波形(Lg＝1.35mH)

图15　　并网逆变器PCC点电压和进网电流波形(Lg＝4.50mH)

当g为640μH时，由于电流环控制作用引入的负阻尼，系统会出现如图13(c)所示的频率为1075Hz的高频谐振．图16为g取640μH时并网逆变器PCC点电压和进网电流波形，可以看出PCC点电压和电流中有明显的高频谐振．1s时投入广域有源阻尼器，高频谐振能够被有效地抑制住．

调整g的值为110μH，系统会出现如图13(d)所示的频率为2350Hz的高频谐振，同样由电流环控制作用所致．图17为g取110μH时并网逆变器PCC点电压和进网电流波形，可以看出谐振频率相比于图16变得更高．同样，1s时投入广域有源阻尼器，谐振也被有效地抑制住了，说明广域有源阻尼器可以有效抑制由电流环控制引起的高频谐振．

图16　　并网逆变器PCC点电压和进网电流波形(Lg＝640μH)

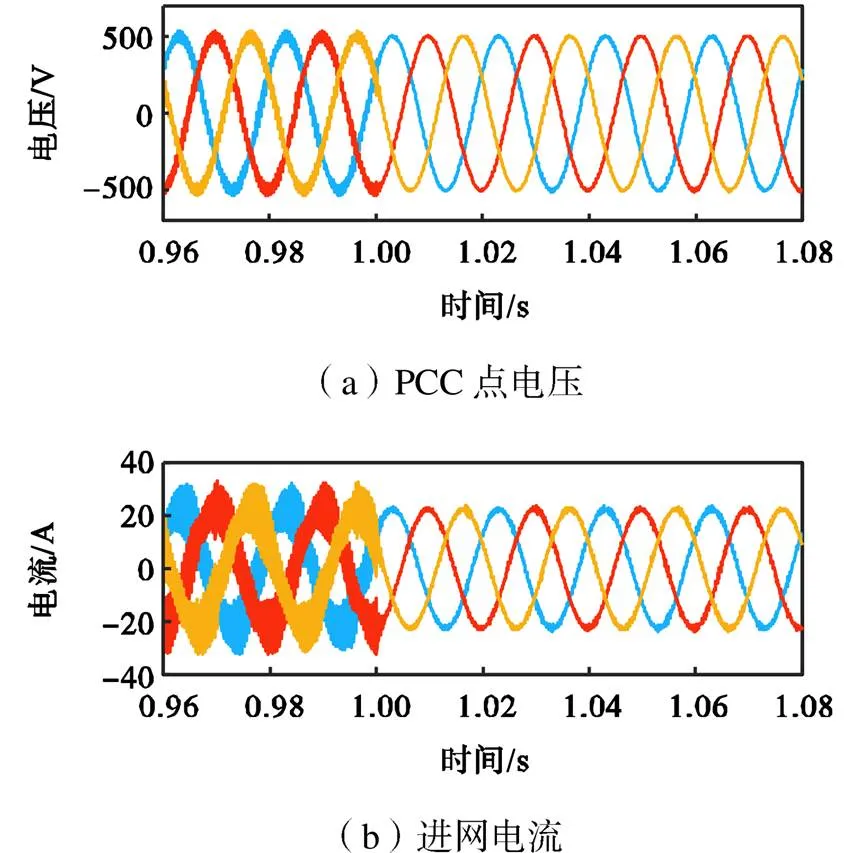
图17　　并网逆变器PCC点电压和进网电流波形(Lg＝110μH)

3.3 系统联络突然变化时的广域镇定仿真

为了验证所设计系统在动态工况下的镇静作用，进行了在系统联络突然变化时的动态过程仿真．当系统联络从弱变强时，并网逆变器进网电流波形如图18所示．可以看出，开始时系统稳定；0.05s时变为弱联络，取g为1.7mH，系统产生频率为470Hz的中频谐振，0.12s时加入广域有源阻尼器，系统得以稳定；0.17s时去掉广域有源阻尼器的同时将系统联络加强，g调小为290μH，产生频率为1750Hz的高频谐振，0.22s时再次加入广域有源阻尼器，系统同样稳定下来了．因此，广域有源阻尼器在系统联络从弱变强时可以有效镇定系统．

当系统联络从强变弱时，并网逆变器进网电流波形如图19所示．开始时系统稳定；0.05s时变为弱联络，g为550μH，系统产生频率为1200Hz的高频谐振，0.1s时加入广域有源阻尼器，系统稳定；0.15s时去掉广域有源阻尼器的同时将系统联络减弱，g调大为2.3mH，产生频率为350Hz的中频谐振，0.22s时加入广域有源阻尼器，系统再次稳定．可见广域有源阻尼器在系统联络从强变弱时可以有效镇定系统.

图18 并网逆变器进网电流波形(联络从弱变强)

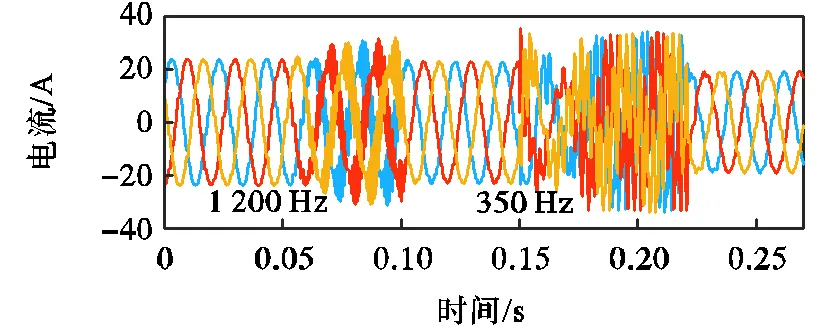
图19 并网逆变器进网电流波形(联络从强变弱)

以上仿真结果表明，并网逆变器与电网弱联络时，PLL、电流环控制会引起广域稳定性问题，广域有源阻尼器能有效抑制由PLL引起的中频谐振以及由电流环控制引起的高频谐振，可以在广域范围内稳定系统．当系统联络突然变化时，无论是系统联络从弱变强，还是从强变弱，所设计的广域有源阻尼器都可以有效实现系统的广域镇定．

4 结 论

本文针对并网逆变器与电网弱联络时，由并网逆变器PLL及电流环控制引起的广域稳定性问题，建立了考虑PLL影响的广域阻抗模型，提出了基于阻抗分析的广域稳定性判据．通过在PCC点并联连接一个广域有源阻尼器，能够有效地解决并网逆变器系统的广域稳定性问题．根据理论分析和仿真验证，可以得出以下结论．

(1) 电网阻抗在较宽的频率范围内变化时，PLL、电流控制器与电网阻抗的相互耦合，使得并网逆变器输出阻抗、相角降低，可能导致广域范围内的不稳定．

(2) 在PCC点并联连接一个广域有源阻尼器，可重塑并网逆变器的输出阻抗并提高其相位，有效镇定系统．

(3) 本文提出的广域有源阻尼器，利用虚拟电阻自适应调节算法设计阻尼电阻，在系统变化时仍能够实现系统广域稳定，可明显提高弱联络下系统的稳定性和适应性．

［1］ 余贻鑫. 面向21世纪的智能电网[J]. 天津大学学报(自然科学与工程技术版)，2020，53(6)：551-556.

Yu Yixin. A brief description of the basics of the smart grid[J]. Journal of Tianjin University(Science and Technology)，2020，53(6)：551-556(in Chinese).

［2］ Blaabjerg F，Teodorescu R，Liserre M，et al. Overview of control and grid synchronization for distributed power generation systems[J]. IEEE Transactions on Industrial Electronics，2006，53(5)：1398-1409.

［3］ Harnefors L，Wang X，Yepes A G，et al. Passivity-based stability assessment of grid-connected VSCs—An overview[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics，2016，4(1)：116-125.

［4］ Wang X，Blaabjerg F，Wu W. Modeling and analysis of harmonic stability in an AC power-electronics-based power system[J]. IEEE Transactions on Power Electronics，2014，29(12)：6421-6432.

［5］ 王萍，王尉，贝太周，等. 数字控制对并网逆变器的影响及抑制方法[J]. 天津大学学报(自然科学与工程技术版)，2016，49(5)：472-479.

Wang Ping，Wang Wei，Bei Taizhou，et al. Effects of digital control on grid-connected inverter and its suppression method[J]. Journal of Tianjin University(Science and Technology)，2016，49(5)：472-479(in Chinese).

［6］ Yang D，Wang X，Blaabjerg F. Sideband harmonic instability of paralleled inverters with asynchronous carriers[J]. IEEE Transactions on Power Electronics，2018，33(6)：4571-4577.

［7］ Wang X，Blaabjerg F. Harmonic stability in power electronic-based power systems：Concept，modeling，and analysis[J]. IEEE Transactions on Smart Grid，2019，10(3)：2858-2870.

［8］ 邢光正，吴琛，陈磊，等. 电压源变换器接入电网的小扰动稳定机理分析[J]. 电力自动化设备，2020，40(9)：42-52，193.

Xing Guangzheng，Wu Chen，Chen Lei，et al. Analysis of small disturbance stability mechanism for grid-connected voltage source converter[J]. Electric Power Automation Equipment，2020，40(9)：42-52，193(in Chinese).

［9］ 吴恒，阮新波，杨东升. 弱电网条件下锁相环对LCL型并网逆变器稳定性的影响研究及锁相环参数设计[J]. 中国电机工程学报，2014，34(30)：5259-5268.

Wu Heng，Ruan Xinbo，Yang Dongsheng. Research on the stability caused by phase-locked loop for LCL-type grid-connected inverter in weak grid condition[J]. Proceedings of the CSEE，2014，34(30)：5259-5268(in Chinese).

［10］ 刘佳宁，于淼，夏杨红，等. 受弱电网影响光伏并网系统不同频段稳定性分析[J]. 电网技术，2020，44(1)：86-95.

Liu Jianing，Yu Miao，Xia Yanghong，et al. Separated frequency stability analysis of grid-connected PV system affected by weak grid[J]. Power System Technology，2020，44(1)：86-95(in Chinese).

［11］ Céspedes M，Sun J. Impedance shaping of three-phase grid-parallel voltage-source converters[C]//2012 Twen-ty-Seventh Annual IEEE Applied Power Electronics Con-ference and Exposition(APEC). Orlando，USA，2012：754-760.

［12］ 李奕欣，赵书强，马燕峰，等. 三相LCL型并网逆变器的阻抗建模及特性分析[J]. 电力自动化设备，2019，39(7)：107-113.

Li Yixin，Zhao Shuqiang，Ma Yanfeng，et al. Impedance modeling and characteristic analysis of three-phase LCL-type grid-connected inverters[J]. Electric Power Automation Equipment，2019，39(7)：107-113(in Chinese).

［13］ Pan D，Ruan X，Bao C，et al. Optimized controller design for LCL-type grid-connected inverter to achieve high robustness against grid-impedance variation[J]. IEEE Transactions on Industrial Electronics，2015，62(3)：1537-1547.

［14］ 王赟程，陈新，陈杰，等. 基于谐波线性化的三相LCL型并网逆变器正负序阻抗建模分析[J]. 中国电机工程学报，2016，36(21)：5890-5898，6033.

Wang Yuncheng，Chen Xin，Chen Jie，et al. Analysis of positive-sequence and negative-sequence impedance modeling of three-phase LCL-type grid-connected inverters based on harmonic linearization[J]. Proceedings of the CSEE，2016，36(21)：5890-5898，6033（in Chinese).

［15］ Zhang C，Wang X F，Blaabjerg F，et al. The influence of phase-locked loop on the stability of single-phase grid-connected inverter[C]//2015 IEEE Energy Conversion Congress and Exposition(ECCE). Montreal，Canada，2015：4737-4744.

［16］ 张志文，曾志兵，罗隆福，等. 基于新型全数字锁相环的同步倍频技术[J]. 电力自动化设备，2010，30(2)：123-126，130.

Zhang Zhiwen，Zeng Zhibing，Luo Longfu，et al. Synchronous frequency multiplication technology based on total digital phase-locked loop[J]. Electric Power Automation Equipment，2010，30(2)：123-126，130(in Chinese).

［17］ Golestan S，Guerrero J M，Abusorrah A，et al. An adaptive quadrature signal generation-based single-phase phase-locked loop for grid-connected applications[J]. IEEE Transactions on Industrial Electronics，2017，64(4)：2848-2854.

［18］ 张学广，付志超，陈文佳，等. 弱电网下考虑锁相环影响的并网逆变器改进控制方法[J]. 电力系统自动化，2018，42(7)：139-145.

Zhang Xueguang，Fu Zhichao，Chen Wenjia，et al. An improved control method for grid-connected inverters considering impact of phase-locked loop under weak grid condition[J]. Automation of Electric Power Systems，2018，42(7)：139-145(in Chinese).

［19］ 高家元，肖凡，姜飞，等. 弱电网下具有新型PLL结构的并网逆变器阻抗相位重塑控制[J]. 中国电机工程学报，2020，40(20)：6682-6697.

Gao Jiayuan，Xiao Fan，Jiang Fei，et al. Grid-connected inverter impedance phase reshaping control with novel PLL structure in weak grid[J]. Proceedings of the CSEE，2020，40(20)：6682-6697(in Chinese).

［20］ 汤建，邹志翔，刘星琪，等. 基于电力电子变压器的逆变器并网系统建模、稳定性分析及控制[J]. 电网技术，2021，45(11)：4224-4233.

Tang Jian，Zou Zhixiang，Liu Xingqi，et al. Modeling，stability analysis and control of grid-connected inverter system using power electronics transformer[J]. Power System Technology，2021，45(11)：4224-4233(in Chinese).

［21］ He J，Li Y W，Bosnjak D，et al. Investigation and active damping of multiple resonances in a parallel-inverter-based microgrid[J]. IEEE Transactions on Power Electronics，2013，28(1)：234-246.

［22］ 曾正，徐盛友，冉立，等. 应用于交流微电网谐振抑制的有源阻尼器及控制[J]. 电力自动化设备，2016，36(3)：15-20.

Zeng Zheng，Xu Shengyou，Ran Li，et al. Active damper and its control for harmonic resonance damping of AC microgrid[J]. Electric Power Automation Equipment，2016，36(3)：15-20(in Chinese).

［23］ Wang X，Blaabjerg F，Liserre M，et al. An active damper for stabilizing power-electronics-based AC systems[J]. IEEE Transactions on Power Electronics，2014，29(7)：3318-3329.

［24］ Zhang C，Wang X F，Blaabjerg F. Analysis of phase-locked loop influence on the stability of single-phase grid-connected inverter[C]//2015 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems(PEDG). Montreal，Canada，2015：4737-4744.

［25］ Sun J. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics，2011，26(11)：3075-3078.

［26］ 刘建锋，李美玉，余光正，等. 考虑VSC系统谐波稳定条件下的LCL滤波器参数优化设计方法[J]. 电力系统保护与控制，2020，48(13)：80-90.

Liu Jianfeng，Li Meiyu，Yu Guangzheng，et al. Optimization design method of LCL filter parameters considering harmonic stability of VSC system[J]. Power System Protection and Control，2020，48(13)：80-90(in Chinese).

Wide-Area Active Damper with Adaptive Virtual Resistance

Li Zhijun1, 2，Jia Yang3，Zhang Jia’an1, 2

(1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment，Hebei University of Technology，Tianjin 300130，China；2. Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province，Hebei University of Technology，Tianjin 300130，China；3. School of Artificial Intelligence，Hebei University of Technology，Tianjin 300130，China)

A grid-connected inverter is the power conversion interface between the distributed generation system and the grid. However，with the wide distribution of power，there are long transmission lines and more isolation transformers between the point of common coupling(PCC)and the grid，resulting in a weakened connection between the grid and the generation system，an increase in the equivalent impedance of the grid，and a weakened grid. When the grid-connected inverter is weakly connected to the grid，the phase-locked loop(PLL)and the control of the current control loop of the grid-connected inverter will introduce negative damping in wide areas，which may cause the system to lose stability in wide areas. To solve this problem，a wide-area impedance model of the grid-connected inverter was developed，considering the influence of the PLL，and a wide-area stability criterion based on impedance analysis was proposed. On this basis，a wide-area active damper is designed by paralleling active dampers at the PCC to stabilize the system and connecting them to the PCC to generate a parallel damping resistance at the PCC to dampen the resonances. When the working conditions of the system change，the virtual resistance is adaptively adjusted by extracting the resonant voltage of the PCC and using the method of harmonic content limitation to achieve system stabilization in a wide area. Finally，the equivalent system model of the grid-connected inverter is built in MATLAB/Simulink，and the effectiveness of the wide-area active damper is verified using time-domain simulation. The simulation results show that when the grid-connected inverter is weakly connected to the grid，the PLL and the control of the current control loop will cause wide-area resonance stability problems. The wide-area active damper can effectively suppress resonance over a wide area and stabilize the system when its connection changes suddenly.

grid-connected inverter；phase-locked loop；current control loop；wide-area active damper；wide-area stability

10.11784/tdxbz202204005

TM712

A

0493-2137(2023)07-0755-12

2022-04-06；

2022-06-10.

李志军（1964—  ），男，博士，教授.

李志军，zhijun_li@263.net.

河北省科技支撑计划资助项目(15212105).

Supported by the Key Technology Support Program of Hebei Province(No. 15212105).

(责任编辑：孙立华)