基于电压频率成分比值差异的MMC-HVDC保护方法
2023-05-27薛士敏刘白冰李翔宇
薛士敏,陈 硕,陈 萧,刘白冰,李翔宇
基于电压频率成分比值差异的MMC-HVDC保护方法
薛士敏,陈 硕,陈 萧,刘白冰,李翔宇
(天津大学电气自动化与信息工程学院,天津 300072)
柔性直流输电系统的快速故障发展给直流保护的研究带来了巨大的挑战,严苛的速动性要求不得不使保护的研究聚焦在故障暂态量上.在高压大容量输电系统中,为更贴合实际工程,线路的频变特性以及行波传输过程是不容忽略的,因此文中以此展开了故障分析.针对单端量保护在耐过渡电阻能力上的不足,文中对保护区内外故障发生时的测量点电压频率特征进行了分析,以过渡电阻为变量观察不同故障情况下的频率比值差异变化趋势,并利用S变换设计了一种基于电压频率成分比值差异的保护方案;其次,根据噪声在S变换下的频谱特点,给出了噪声识别判据;最后,在PSCAD/EMTDC 仿真平台上搭建了四端柔性直流输电系统模型对所提方法进行了验证.结果表明,区内外故障下的电压频率成分比值存在明显差异,所提保护方案可以准确识别线路不同位置的短路故障,并可判断故障极.与基于电压变化量和高频段能量的保护方法相比,文中方法具备更高的耐过渡电阻能力.即便是远距离高阻故障,保护方法也具备明显的区分度,可见,所提方法可以更好地适用于大容量远距离输电系统.同时,在不同信噪比的噪声环境下,保护方法仍旧可以准确识别出噪声以及故障.保护方法可以在2ms内完成故障识别,满足柔直系统的速动性要求,可作为系统运行的主保护.
柔性直流输电;单端量保护;S变换;高阻故障
能源是人类社会发展的主要动力,化石能源的使用给全球环境造成了严重的影响,为了有效利用风能和太阳能等清洁能源,必须采用新型电网技术以满足未来能源的发展需求[1-2].柔性直流输电相比于传统的直流输电技术来说,没有换相失败和无功补偿问题,无功有功可独立调节,受端系统可以是无源网络,谐波水平低,功率可双向流动,且可实现多端直流系统[3-4].模块化换流器(MMC)的出现更是推动了柔性直流输电的发展.但是基于模块化换流器的柔性直流输电技术(MMC-HVDC)的发展需要完善相应的继电保护理论,从而保证直流侧故障的可靠切除.
目前直流系统中的保护方案可以分为基于单端量的保护以及双端量的保护.其中,基于单端量的保护无需考虑通信延迟以及通信同步的问题,动作速度较快,在直流系统中一般可作为主保护.文献[5-6]利用限流电抗器对电压变化率的衰减作用识别区内外故障,文献[7-8]利用限流电抗器电压构造保护方案,文献[9]利用限流电抗器的电压变化率构成保护方法,但是在高阻故障时灵敏度不足.基于频域的保护方法可以更好地反映故障的本质特征,文献[10-13]利用边界元件的高频阻滞特征来实现故障的判定,由于采用单一频段的信息构造保护,在远距离高压系统中,同样也面临区内高阻故障和区外故障难以区分的问题,且易受噪声干扰的影响.同时,线路的频变特性与分布参数特性影响着故障电气量的频域特征,这在高压长距离输电系统中是不容忽视的.双端量保护相比于单端量保护有着更高的可靠性,双端量保护主要是利用线路两侧的电气量在信息上的交互实现故障的判别,常常作为交流系统中的主保护.文献[14]利用两端反行波幅值识别故障,文献[15-16]根据线路两端电压电流关系构成纵联保护,文献[17-18]利用两侧的固有频率差异构成频差保护,但是由于柔性直流电网的快速动作要求,这些保护方法不能作为柔直输电系统中长线路的主保护.
综上,针对目前柔直保护存在的问题,笔者旨在设计出快速、可靠以及灵敏的保护方法,以满足高压大容量远距离输电系统的安全运行需求.考虑到单端量保护在速动性上以及频域分析在反映故障特征上的优势,笔者结合了线路的频变参数特性以及行波传输过程,对区内外故障时测量点电压的频率特征进行了分析,并构造了基于电压频率成份比值差异的保护方案,最后在仿真中验证了所提保护方案的耐过渡电阻能力和抗噪能力.
与现有频域保护方法相比,笔者保留了单端量保护的速动性优势,不再采用单一频段构造保护,而是利用低频成分与高频成分之间的比值差异来大幅提高保护的耐过渡电阻能力,同时以此保证了保护的抗噪能力.行波高频成分经长距离线路传输后的幅值会大幅降低,过低的高低频比值并不能很好地提高保护灵敏性,因此不同于高频比低频的方法,文中采用的低频比高频在远距离高阻故障时也拥有显著的灵敏度,可以更好地反映高压直流系统中的高阻故障.
1 MMC-HVDC系统结构
图1为四端柔性直流输电系统拓扑结构.直流侧采用架空线构成环形输电网络,线路两端连接有直流断路器以及限流电抗器,保护安装于限流电抗器的线路侧.4个换流站经过金属回线与接地点相连接.

图1 四端柔性直流输电系统
图2为换流站内部拓扑结构,换流站采用对称双极接线方式,接地出口串有限流电抗器,金属回线从两个换流器中间引出,换流器子模块皆采用常见的半桥结构.

图2 换流站内部拓扑
2 故障电压的频率特性
当直流线路发生故障后,故障点将产生向线路两端传输的故障电压、电流行波,之后在保护安装处发生折反射.从频域的角度来看,故障行波含有丰富的频率成分.在初始行波向保护安装处传播的过程中,线路或限流电抗器对行波不同频率成分的衰减程度不同,本节将分析在区内外故障发生时测量电压的频率成分差异.
2.1 区内故障
考虑到正负极线路之间的耦合关系,需要对正负极电压进行解耦.如图3所示,保护安装处的0模和1模故障分量电压可表示为

式中ΔUp、ΔUn分别为保护安装处的正负极电压增量,后文分析电压均指电压增量.区内正极线路内部故障的1模等效电路如图3所示,其中eq=60/、eq=2arm/3分别为换流器的等效电容和等效电感,0为子模块电容,arm为桥臂电感,为桥臂子模块数量,暂不考虑相邻线路的影响.令c1为线路的1模特性阻抗,在考虑线路的频变参数特性时,它是频率的函数.ΔU1()为故障点1模电压阶跃信号的初值.


式中:d1()为线路的1模传播函数;ρ1()为行波在保护安装处的反射系数.设Zs()为侧母线背后系统的等效阻抗.则ρ1()的计算式为

当线路末端发生故障时,故障电路如图4所示.

图4 区内末端故障1模等效电路


式中Zs()为侧母线背后系统的等效阻抗.


2.2 区外故障
当对侧母线发生正极接地故障时,故障等效电路如图5所示.

图5 正向区外故障1模等效电路

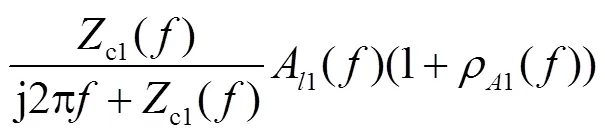
当背侧母线发生正极接地故障时,故障等效电路如图6所示.

图6 反向区外故障1模等效电路

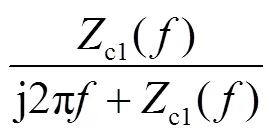
2.3 故障特性分析
传输线路的特性阻抗和传播函数是频率的函数,没有精确的解析表达式.为了描述传输线路参数随频率的变化关系,需要在拉普拉斯域上对特性阻抗和传播函数做相应的近似处理.拟合的有理函数需要较好地反映特征阻抗和传播函数的频率特性.根据文献[19-20]中对Marti模型的处理办法,可采用拉普拉斯域下的部分分式ceq()和a()来拟合线路末端故障时的特性阻抗和传播函数.拟合形式分别为


式中:k为比例系数;p为极点;为极点的个数.线路末端故障时的各参数拟合结果如表1和表2所示.
图7和图8分别是线路末端故障时对特性阻抗和传播函数拟合结果.可见1模阻抗随频率变化的值近似为恒定,计算时,1模阻抗取为243.8Ω.相比于0模分量,1模分量受线路衰减影响较小.
表1 参数拟合结果

Tab.1 Fitting results of Zceq(s) parameters
表2a()参数拟合结果
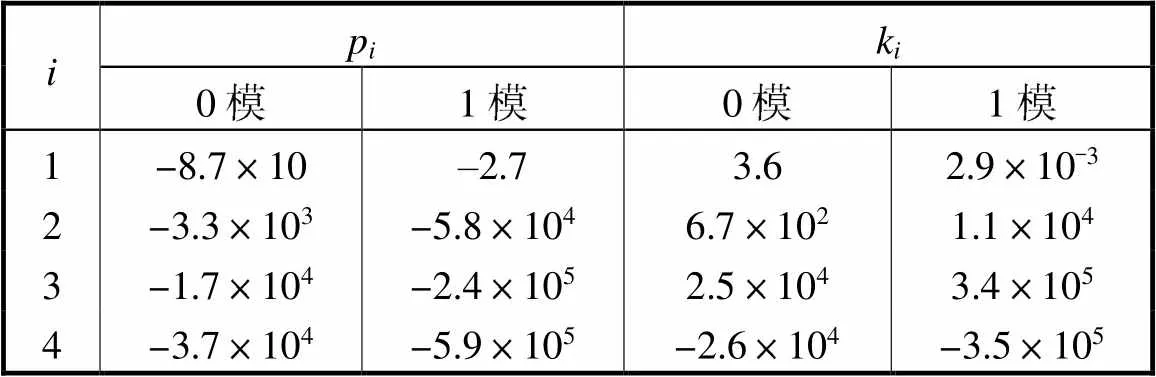
Tab.2 Fitting results of Pa(s) parameters
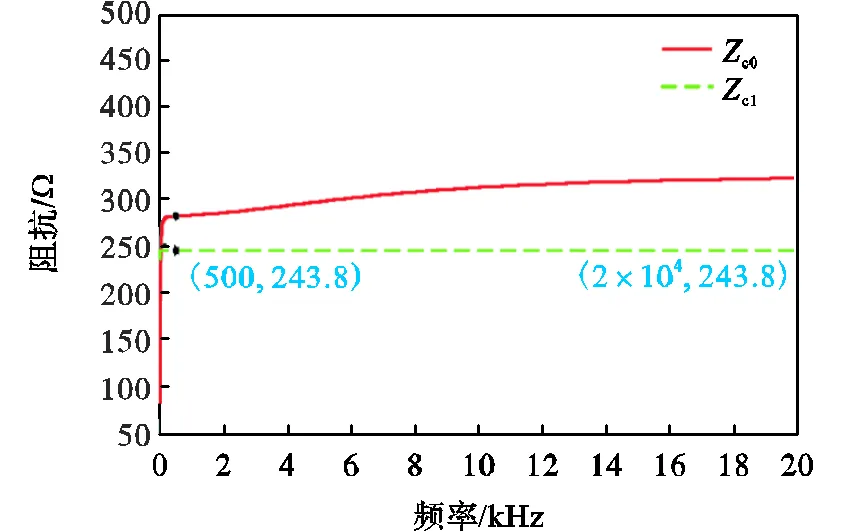
图7 特性阻抗拟合结果

图8 传播函数拟合结果
区内故障时,行波仅受到线路的衰减作用,而区外故障时,行波到达测量点前将穿过线路电抗器,所以行波将受到电抗器和线路的衰减作用.由于线路电抗器对行波中频率成分的衰减是不同的,所以行波经过线路两侧的电抗器后,行波中各个频率成分的含量会发生不同程度的变化.频率越高,行波中该频率成分的幅值衰减越大,这就使较低频段与较高频段之间的幅值差异将会增大.因此本节将选取合适的频率成分,通过代入前文的特性阻抗和传播函数拟合结果来分析幅值差异随过渡电阻的变化趋势,以观察过渡电阻对幅值差异的影响.
为控制变量的个数,使分析的自变量仅为过渡电阻,同时使所选频率成分之间的幅值差异最大,本文选取1=500Hz和2=20000Hz的频率进行分析,这也是在本文采样频率和数据窗长下S变换所能获得的最小频率(非直流分量)和最大频率,仿真采样频率为40kHz,根据奈奎斯特采样定理,S变换所能取得的最大频率为采样频率的一半,即20kHz,S变换的数据窗长为2ms,共80个数据,S变换矩阵的频率间隔为40kHz/80=0.5kHz,故S变换取得的最小频率(非直流分量)为0.5kHz.根据图8可以取得两种频率成分下全长线路的1模传播函数A1().所分析线路的两侧换流器参数相同,则Zs=Zs,如不同也可代入相应参数分析.根据式(2)、式(4)、式(6)以及式(7)的测量电压关系式,并代入频率1和2,则可得出在区内故障、区内线路末端故障、区内线路首端故障、正向区外故障以及反向区外故障下,测量电压频率成分1和2的幅值比分别为
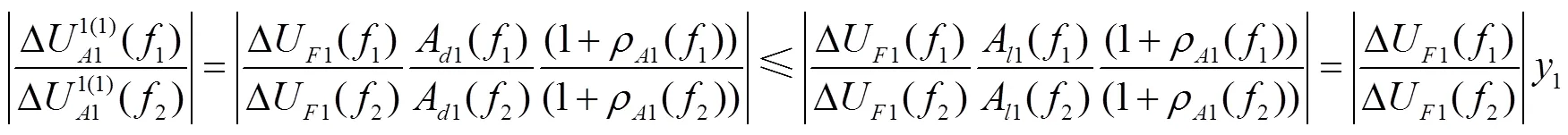



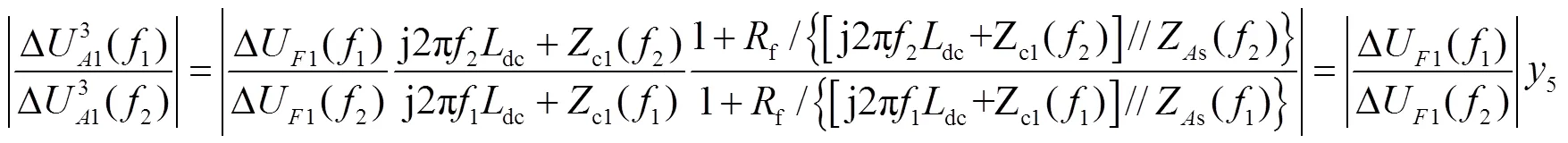
式中:ΔU1为故障点处的电压初值;A1为线路的1模传播函数;ρ1为电抗器处的行波反射系数;c1为线路的1模特性阻抗;f为过渡电阻;Zs和Zs分别是侧系统和侧系统的等效阻抗值;dc为线路电抗器.在式(10)中,当行波经线路全长传输时(=),较低频段与较高频段之间的幅值差异最大.式(10)中,两种测量电压的频率成分比值可以写成故障点处两种频率成分的比值再乘以一个系数的形式,令该系数为1.同理,将式(11)~式(14)也写成故障点处两种频率成分的比值再乘以一个系数的形式.则在区内故障、区内线路末端故障、区内线路首端故障、正向区外故障以及反向区外故障之间的幅值比大小就可以通过所化简的系数1、2、3、4和5来比较.
通过代入以上参数,则1、2、3、4和5随过渡电阻的变化趋势如图9所示.
根据图9可以看出在不同过渡电阻下,1和2的比值在区内、区外故障时具有明显差异,基于此规律构造保护原理可以大大提高保护的耐过渡电阻能力.虽然随着过渡电阻的增大,区外故障的频率比值会有所降低,但是与区内仍有可靠的区分度.
对于对称双极系统,双极故障可以看作正负极同时发生单极接地故障,分析方法与单极故障类似.故障的选极可以根据0模分量的变化进行判断,即
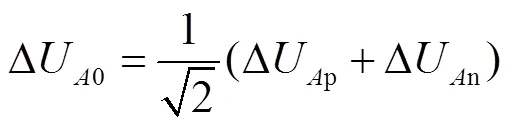
由式(15)可见正极故障时,ΔUA0<0;负极故障时,ΔUA0>0;双极故障时,ΔUA0≈0.
3 S变换基本原理
S变换作为一种全新的频域分析方法,可以克服短时傅里叶变换因窗函数大小不变导致分辨率不能动态变换和小波变换的尺度与频率不能对应的缺点[21].
信号()一维连续S变换可定义为

式中(-,)为高斯窗函数,在频率较高时,窗口长度短,具有较高的时间分辨率,反之,在频率较低时,窗口长度长,具有较高的频率分辨率.

信号()的离散S变换可以由其离散傅里叶变换得到,()的离散傅里叶变换可以表示为

式中:为采样点的个数;为采样周期;=0,1,2,…,-1;受采样频率的影响,根据奈奎斯特定理,=0,1,2,…,/2,其中,=0代表直流分量.信号()的离散S变换为
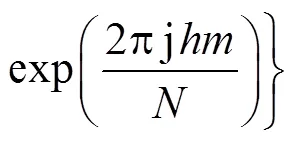
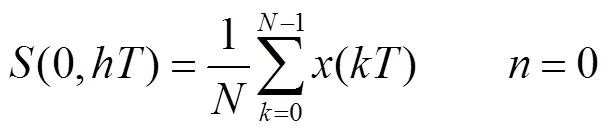
可以看出信号经离散S变换后得到的是一个复数矩阵,行对应不同的离散频率,列对应不同的离散时间,行与行之间代表的频率差为1/,列与列之间代表的时间差为.
4 保护方案设计
4.1 保护启动
保护的启动判据应保证保护启动的灵敏性,在故障发生后,故障电压行波将会向线路两边传输,在短暂的行波传输延时后,测量点的电压会迅速下降.考虑到正常运行时的直流电压波动,本文定义偏差电压Δ1、Δ2以及正常稳定电压a分别为


式中u()为当前采样时刻的电压值,当连续两个采样时刻的电压值与正常稳定电压出现较大偏差时,保护启动.

式中Δset为保护启动阈值,根据正常运行时的偏差电压来决定.
4.2 故障判定
利用S变换提取频率1和2,设1和2分别为1和2在S变换矩阵中对应的行数,0为保护启动时刻.令

考虑到噪声信号属于高频信号,在S变换下,其高频段幅值大于较低频段的,所以当1≤1,可认为发生了噪声干扰;当1<1<set时,则线路区内可能发生了故障.
根据0模分量的大小进行故障选极.

0≤-set可认为发生了正极接地故障,0≥set可认为发生了负极接地故障,-set<0<set时则认为双极故障.保护应在本极故障和双极故障时动作,即0<set时.本文仿真以正极保护为例.
4.3 保护流程
根据以上分析,保护流程如图10所示.
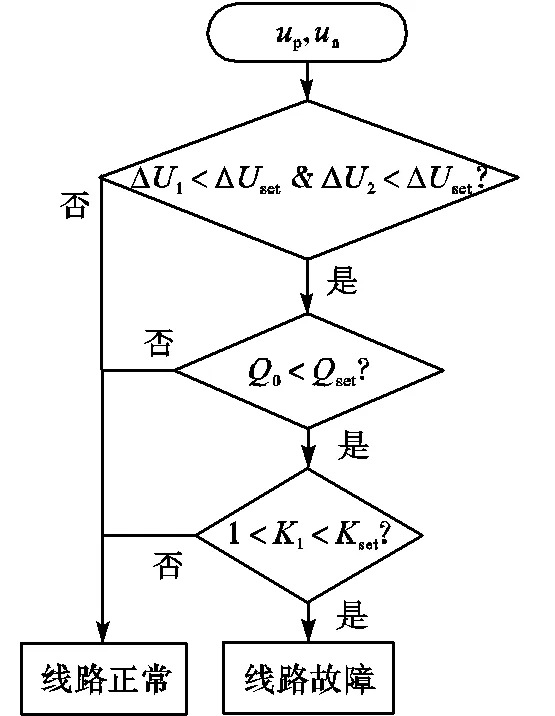
图10 保护流程
5 仿真分析
5.1 仿真参数
本文在仿真PSCAD/EMTDC中搭建图1所示的对称双极大地回路接线方式多端柔性直流输电系统,电压等级±500kV,线路采用频变模型.系统的相关参数如表3和表4所示.
本文采用的仿真步长和采样步长均为25μs,数据窗长2ms(故障前和故障后各1ms).因此S变换得到的是一个41×80的矩阵,可知1=41和2=2.保护只需计算出需要的行数,无需计算出整个矩阵.考虑到启动的灵敏性,启动阈值Δset取为20kV.set和set需要根据仿真来确定,以保证1在区内外故障时具有明显差异度,并满足选极需要,本文设置保护整定值set=900,set=10kV.
表3 系统主要参数

Tab.3 Main parameters of the system
表4 线路参数

Tab.4 Parameters of lines
5.2 仿真验证
5.2.1 区内外故障
当直流线路中点发生故障后,测量点电压的时频分布如图11所示(图中所用窗长10ms,采样频率40kHz,故障时刻1.3ms,图中不包含100Hz以下的低频成分).可见在故障发生后,保护安装处含有丰富的频率信息,这些频率信息为保护的构造提供了重要的条件.时间轴的边界处具有较高的幅值,这是由S变换边界效应造成的.实际工程中应该将数据窗两端某些数据舍弃,或者对时间窗做平滑处理.

图11 电压时频分布
表5为不同故障位置处的仿真结果,对于正极故障,0均小于0,保护可正确识别.在发生双极故障时,均满足0<set,则保护同样可以切除区内故障.对于负极故障,0均大于set,保护可靠不动作.在线路区内不同位置发生不同类型故障时,均满足1<1<set,区外故障时的1远大于set,可见保护可以准确识别区内外故障.
表5 不同位置故障仿真结果

Tab.5 Simulation results of different fault locations
5.2.2 过渡电阻
耐过渡电阻能力是衡量高压直流保护性能的重要标准,保护应能准确识别区内的各类高阻故障,并在区外故障时不会错误动作.为了验证所提保护方法的耐过渡电阻能力,本节将先后分析基于电压变化量和高频能量的保护方法,通过对比,最后再说明本文方法在高阻故障下的动作情况.
当线路末端发生高阻故障时,保护启动后0.5ms内电压变化量绝对值的和∑│Δ│如图12所示.可以看出,随着过渡电阻的增大,区内故障的电压变化量与最严重区外故障(保护背侧母线故障)的差别逐渐减小,在过渡电阻达到300Ω以上时,末端高阻故障将不易于与区外故障区分.
行波经线路两侧的限流电抗器会发生频率衰减,尤其是高频成分衰减更为明显.在这里以小波变换为例,电压高频分量系数1通过Mallat算法的第1层分解获得.同时考虑到小波变换引起的边界效应,在不进行平滑处理的情况下,舍弃数据窗两端的数据.由此可得频率段10~20kHz在保护启动后0.5ms内的高频能量如图13所示.

图12 电压变化量计算结果

图13 高频段能量计算结果
可见,相较于电压变化量,基于频域的高频量保护有着更高的耐过渡电阻能力,甚至可以达到500Ω以上.但即便是依据高频段能量构造保护,在过渡电阻达到一定值时,区内高阻故障与较严重的区外故障之间的差异也会逐渐减小(如图13中的末端800Ω故障).本文仿真系统的线路长度最长为206.6km,对于更长的输电线路,线路对行波高频分量的衰减作用会逐渐增大,即逐渐逼近于限流电抗器对高频分量的衰减作用.此时小于500Ω的过渡电阻有可能使末端故障与背侧区外母线故障的高频特征相近,因此,基于高频段能量的保护方法的耐过渡电阻能力会进一步降低.
图14是本文保护方法的仿真结果,可以看出,本文所提方法可以准确识别区内不同位置下的高阻故障,并与区外故障有着较大的区分度.即便是过渡电阻达到1500Ω时,保护依据可以保证足够的灵敏度,这也说明本文方法受过渡电阻的影响较小,进而可以适应于更长距离的输电系统.
从图9中可以看出,当区外故障时,随着过渡电阻的增大,1的值会逐渐降低,所以有必要验证区外高阻故障和区内故障的差异度.如图14所示,在不同过渡电阻大小的区内外故障发生时,区内外仍具有很大的差异度.同时,对侧区外和背侧区外500Ω接地故障时的计算启动值分别为21.758kV/s和29.063kV/s,已经很接近于启动阈值.而对于过渡电阻较大的区外高阻故障,其故障特征很微小,并不足以使保护启动.

图14 不同故障位置及不同过渡电阻的仿真结果
5.2.3 噪声干扰
噪声作为一种剧烈变化的高频信号可能会使保护感受到较大的电气量变化过程,基于电气量突变或是高频量的保护都会受到影响,所以有必要验证保护方法的抗噪能力.
图15是当信噪比为20dB的噪声信号出现在正常运行状态下时,保护测得的时域电压波形.可以看出噪声的出现使得电压波动剧烈,这极易引起保护误动作.噪声信号叠加到故障信号中会影响原始信号中的故障信息,如图16所示,经20dB信噪比噪声叠加后的测量电压波形会产生小幅振荡,此时保护应能正确动作于故障.
表6为1分别在不同信噪比以及不同运行情况下的5次仿真结果.从表中可以看出,在正常运行时1均小于1,说明噪声的出现并不会引起本文保护的误动作.同时,当故障信号与不同信噪比的噪声信号叠加时,保护依然满足故障判据并准确识别故障.

图15 正常运行状态
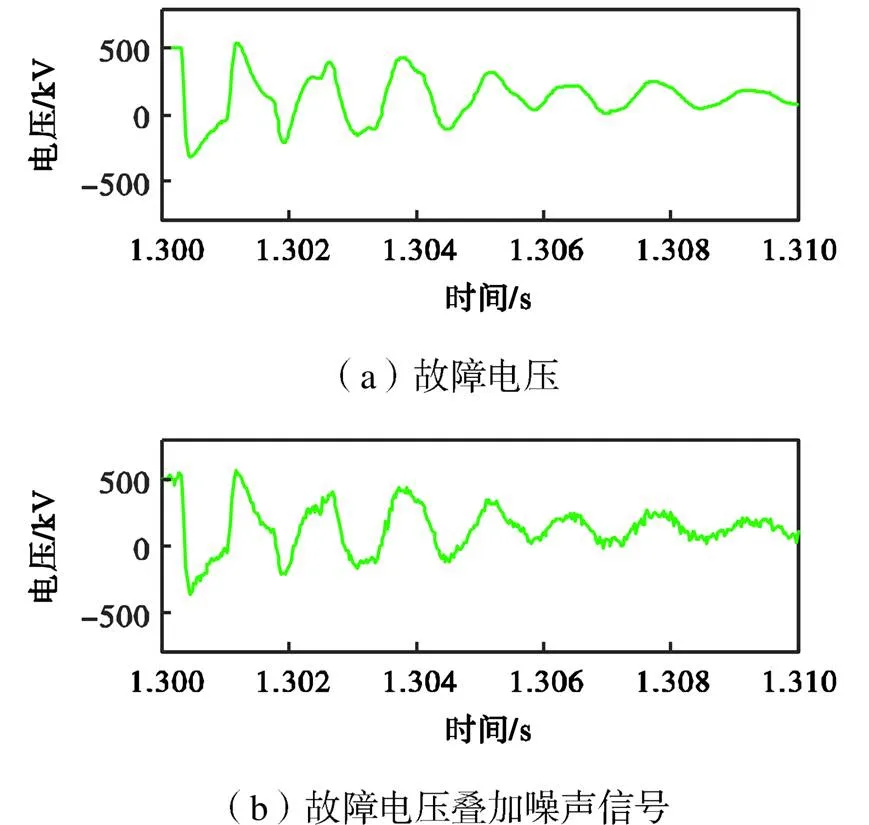
图16 故障状态
表6 噪声仿真结果

Tab.6 Simulation results under noise
算法总共大约需要46860×2/41≈2286次乘法.DSP芯片可在一个指令周期内完成一次乘法运算,目前的TM320系列处理器的指令周期在20ns以下,即保护可以在2286×20×10×10-6≈0.05ms完成乘法运算,再计及其他运算处理时间(行波最大传输时间0.7ms,故障后的数据窗长1ms,光电转换及测量延时0.1ms),因此保护动作时间仍不会超过2ms,满足速动性要求,给直流断路器的动作留下了较为充分的时间.
6 结 论
本文通过考虑线路的频变特性和行波的传输过程来分析故障电压在不同过渡电阻下的频率特征,并设计了相应保护方案,所得结论如下.
(1) 由于限流电抗器的存在,故障行波中的500Hz和20000Hz频率成分的比值差异在区外故障时将会明显增大,根据二者的比值可以有效区分区内外故障.在远距离高压输电系统中,线路对行波高频分量的衰减作用不容忽略,在高阻故障发生时,仅依靠高频段幅值或能量构造保护已经不能保证足够的耐过渡电阻能力.与现有频域方法相比,采用频率成分比值差异可以保证在高阻故障下,保护仍具备可靠的识别能力.
(2) 根据噪声在S变换下的频率分布特征可以实现噪声干扰的有效区分,且在噪声环境下保护仍然可以准确识别故障.
(3) 所提保护阈值需要借助仿真来确定,这是文中存在的不足之处.保护方案耐过渡电阻能力很高,对于阻值很大的高阻故障,工程中可根据实际运行需求来决定该故障是否应该立刻被切除.
[1] Chu S,Majumdar A. Opportunities and challenges for a sustainable energy future[J]. Nature:International Weekly Journal of Science,2012,488(7411):294-303.
[2] 刘振亚,张启平,董 存,等. 通过特高压直流实现大型能源基地风、光、火电力大规模高效率安全外送研究[J]. 中国电机工程学报,2014,34(16):2513-2522.
Liu Zhenya,Zhang Qiping,Dong Cun,et al. Efficient and security transmission of wind,photovoltaic and thermal power of large-scale energy resource bases through UHVDC projects[J]. Proceedings of the CSEE,2014,34(16):2513-2522(in Chinese).
[3] Flourentzou N,Agelidis V G,Demetriades G D. VSC-based HVDC power transmission systems:An overview[J]. IEEE Transactions on Power Electronics,2009,24(3):592-602.
[4] 徐 政,陈海荣. 电压源换流器型直流输电技术综述[J]. 高电压技术,2007,33(1):1-10.
Xu Zheng,Chen Hairong. Review and applications of VSC HVDC[J]. High Voltage Engineering,2007,33(1):1-10(in Chinese).
[5] Sneath J,Rajapakse A. Fault detection and interruption in an earthed HVDC grid using ROCOV and hybrid DC breakers[J]. IEEE Transactions on Power Delivery,2016,31(3):973-981.
[6] Sneath J,Rajapakse A D. DC fault protection of a nine-terminal MMC HVDC grid[C]// 11th IET International Conference on AC and DC Power Transmission. Birmingham,UK,2015:1-8.
[7] 杨赛昭,向 往,文劲宇. 基于限流电抗器电压差异性的架空柔直电网故障检测方法[J]. 中国电机工程学报,2019,39(22):1196-1211.
Yang Saizhao,Xiang Wang,Wen Jinyu. A fault protection scheme based on the difference of current-limiting reactor voltage for overhead MMC based DC grids[J]. Proceedings of the CSEE,2019,39(22):1196-1211(in Chinese).
[8] 周家培,赵成勇,李承昱,等. 基于直流电抗器电压的多端柔性直流电网边界保护方案[J]. 电力系统自动化,2017,41(19):89-94.
Zhou Jiapei,Zhao Chengyong,Li Chengyu,et al. Boundary protection scheme for multi-terminal flexible DC grid based on voltage of DC reactor[J]. Automation of Electric Power Systems,2017,41(19):89-94(in Chinese).
[9] Li Rui,Xu Lei,Yao Liangzhong. DC fault detection and location in meshed multiterminal HVDC systems based on DC reactor voltage change rate[J]. IEEE Transactions on Power Delivery,2017,32(3):1516-1526.
[10] Xiang W,Yang S,Xu L,et al. A transient voltage-based DC fault line protection scheme for MMC-based DC grid embedding DC breakers[J]. IEEE Transactions on Power Delivery,2019,34(1):334-345.
[11] 李 斌,何佳伟,李 晔,等. 基于边界特性的多端柔性直流配电系统端量保护方案[J]. 中国电机工程学报,2016,36(21):5741-5749.
Li Bin,He Jiawei,Li Ye,et al. Single-ended protection scheme based on boundary characteristic for the multi-terminal VSC-based DC distribution system[J]. Proceedings of the CSEE,2016,36(21):5741-5749(in Chinese).
[12] Mehrabikooshki M,Mi Rh Osseini S S,Jamali S. Single-end protection scheme for LCC HVDC transmission lines based on high frequency components of transmission line current[C]//2020 14th International Conference on Protection and Automation of Power Systems. Tehran,Iran,2019:1-8.
[13] Shu H,Tian X,Dai Y. The identification of internal and external faults for ±800kV UHVDC transmission line based on S-transform of the polarity wave[C]// 2010 2nd International Conference on Industrial and Information Systems. Dalian,China,2010:288-292.
[14] Tang L,Dong X,Luo S,et al. A new differential protection of transmission line based on equivalent travelling wave[J]. IEEE Transactions on Power Delivery,2017,32(3):1359-1369.
[15] 李小鹏,何正友,武 骁. 基于S 变换能量相对熵的高压输电线路极性比较式纵联保护[J]. 电网技术,2014,38(8):2250-2256.
Li Xiaopeng,He Zhengyou,Wu Xiao. Polarity comparison pilot protection based on S-transform energy relative entropy for high voltage transmission lines[J]. Power System Technology,2014,38(8):2250-2256 (in Chinese).
[16] 高淑萍,胡振宇,张保会,等. 一种适用于MMC-HVDC直流输电线路的保护新原理[J]. 电力系统保护与控制,2018,46(13):13-20.
Gao Shuping,Hu Zhenyu,Zhang Baohui,et al. A new relay protection principle of MMC-HVDC transmission lines[J]. Power System Protection and Control,2018,46(13):13-20(in Chinese).
[17] 武 骁,何正友,彭少博,等. 基于行波固有频率的特高压直流输电线路纵联保护方法[J]. 电力系统保护与控制,2013,41(11):67-73.
Wu Xiao,He Zhengyou,Peng Shaobo,et al. A UHVDC transmission line pilot protection method based on natural frequencies of traveling wave[J]. Power System Protection and Control,2013,41(11):67-73(in Chinese).
[18] 李小鹏,何正友,陈 双,等. 基于电流行波固有频率的输电线路纵联保护方法[J]. 中国电机工程学报,2013,33(28):121-131.
Li Xiaopeng,He Zhengyou,Chen Shuang,et al. A novel pilot protection for transmission lines based on natural frequencies of current[J]. Proceedings of the CSEE,2013,33(28):121-131(in Chinese).
[19] Dufour C,Le-Huy H. Real-time simulation of power transmission lines using Marti model with optimal fitting on dual-DSP card[J]. IEEE Transactions on Power Delivery,1996,11(1):412-419.
[20] 薛士敏,孙亚冰,刘白冰,等. 基于Marti 模型的柔性直流输电系统纵联行波差动保护[J]. 中国电机工程学报,2019,39(21):6288-6299.
Xue Shimin,Sun Yabing,Liu Baibing,et al. Longitudinal travelling wave differential protection for flexible HVDC system based on Marti model[J]. Proceeding of the CSEE,2019,39(21):6288-6299(in Chinese).
[21] Stockwell B R,Mansinha L,Lowe R. Localization of the complex spectrum:The S transform[J]. IEEE Transactions on Signal Processing,1996,44(4):998-1001.
An MMC-HVDC Protection Method Based on the Difference in the Ratios of the Voltage-Frequency Components
Xue Shimin,Chen Shuo,Chen Xiao,Liu Baibing,Li Xiangyu
(School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China)
The rapid failure development of flexible DC transmission systems has introduced significant challenges to the research of DC protections,and the strict requirements of quick motion must enable the research of protections to focus on the fault transient quantity. To optimally fit the actual project,the frequency-dependent characteristics of the line and the traveling wave transmission process cannot be ignored in the high-voltage large-capacity transmission system. Thus,we perform a fault analysis in this study. Aiming at the insufficiency of the single-ended protection in withstanding transition resistance,this paper analyzes the voltage and frequency characteristics of the measurement point when faults occur inside and outside the protected area and uses the transition resistance as a variable to observe the changing trend of the frequency ratio difference under different fault conditions. A protection scheme,based on the difference in the ratios of the voltage-frequency components inside and outside the protection zone,is designed by using the S-transform. Next,the noise identification criterion is provided according to the frequency spectrum characteristics of noise under the S-transform;Finally,a four-terminal flexible DC transmission system model is built on the PSCAD/EMTDC simulation platform to verify the proposed method. The results show obvious differences in the ratios of voltage-frequency components under faults inside and outside the zone. The proposed protection scheme can accurately identify short-circuit faults at different positions of the line and judge the fault pole. Compared with the protection method based on voltage variation and high-frequency energy,the method in this paper demonstrates a higher resistance to transition resistance. The protection method displays obvious discrimination even in the case of long-distance high-resistance faults. Thus,it can perform better in large-capacity long-distance power transmission systems. Concurrently,in the noise environment with different signal-to-noise ratios,the protection method can still accurately identify noise removal and faults. The protection method can complete the fault identification within 2ms and meet the quick-action requirements of the flexible straight system. Thus,it can be used as the main protection of the system operation.
flexible DC transmission;single-ended protection;S-transform;high-resistance fault
10.11784/tdxbz202204045
TM773
A
0493-2137(2023)07-0745-10
2022-04-20;
2022-08-03.
薛士敏(1980— ),女,博士,副教授,xsm@tju.edu.cn.
陈 硕,2019234251@tju.edu.cn.
国家电网有限公司总部科技项目(KJ21-1-66).
Supported by the Science and Technology Project of SGCC(No. KJ21-1-66).
(责任编辑:孙立华)
