利用人工植林削减古塔风荷载的风洞试验
2023-05-26李雨航李爱群
邓 扬,李雨航,李爱群,3
(1.北京建筑大学 土木与交通工程学院,北京 100044;2.北京未来城市高精尖创新中心,北京 100044;3.东南大学 土木工程学院,江苏 南京 211189)
古木结构是中国建筑文化遗产的重要组成部分,是华夏文明历史与文化的载体,具有极高的历史、文化与艺术价值[1]。其中,应县佛宫寺释迦塔(简称应县木塔)是中国现存最高、最古老的木塔,因其复杂的结构构造成为中国乃至世界古代木构建筑的典范[2];然而,由于受到自然老化、地震及其风荷载等作用的影响,使得木塔产生了不同程度的病害,特别是木塔二层西南角柱倾斜严重,若倾斜持续发展,会有极大的倒塌风险[2-3]。中国文化遗产研究院的现场监测与检测发现,木塔塔址主导风向为西南方向,与木塔倾斜方向具有一定相关性[3]。风荷载的持续作用会使木塔的倾斜进一步发展,有效控制或缓解其在风作用下的倾斜损伤已刻不容缓[4]。
已有学者针对这一问题做出了一些有益的探索,王世仁[5]提出了落架大修方案,王瑞珠等[6]提出了介入式保护方案并进行了评估,Zhang等[7]开展了二层紧急加固的有限元计算。总的来看,上述方法的基本思想均是增强木塔结构自身抵抗外界水平荷载的抗力。除此之外,作者提出一种缓解木塔风致倾斜损伤的新思路:在木塔周围进行人工植林,进而改变木塔周围的风场,减小作用在木塔结构表面的风荷载,实现缓解木塔风致倾斜损伤的目的。
人工建设防护林以减少风速从而实现防风固沙的方法已经应用于中国“三北”防护林体系工程建设中,该方法有效改善了大空间尺度区域的风场环境[8]。Rui等[9]通过合理布置树林有效改变了建筑物周围风场,在建筑物周围关键区域减小风速。国内外学者针对人工植林改善现代建筑周围风场环境的问题开展了研究,其核心思想是利用建筑群与周围环境的风场干扰效应[10],主要研究方法包括现场实测[11]、计算流体力学(computational fluid dynamics,CFD)数值模拟[9,12]与风洞试验。其中,风洞试验是风工程中准确且成熟的方法,可以弥补实测与CFD技术的缺点,如天气影响[13]、湍流模拟参数[14-15]与树木模拟方法[16-18]等。近年来,Cheng等[19]对不同树木布置方式下的风场分布规律开展了风洞试验研究,Ma等[20]采用风洞试验研究了遮挡物与风场之间的关系。
然而,对于应县木塔这类“独一无二”的高耸古木塔结构,现有人工植林影响建筑风场的研究成果仍难以有效支撑缓解木塔风致损伤,主要原因:1)现有研究主要面向现代建筑[9,21],而针对具有复杂外形的高耸古木结构的研究较少;2)人工植林风洞试验研究缩尺比大多在1∶200以下[22],特别是树木模型尺寸较小,误差较大,针对大缩尺比的树木风洞试验模拟方法鲜有介绍。基于上述认识,本文提出利用人工植林减小高耸古木塔的风荷载,从而实现缓解其倾斜损伤持续发展的新思路。相较于其他方法,本文方法具有成本低、非接触、可更换与干扰小等优势,不会对木塔造成直接损伤。
本文以应县木塔为研究对象,采用大比例尺(1∶50)的精细化木塔刚性模型和树木模型,开展了基于人工植林技术的木塔风洞测压试验。研究了大比例尺下,高大乔木树林的模型制作方法;分析了有无树木条件下,木塔的风压特性及其分布规律;采用风洞试验结果计算了不同的树木高度、距木塔距离与布置宽度等条件下的风荷载层间力与层倾覆弯矩,并分析了基底剪力与弯矩的减小率,在此基础上给出了植林布置的建议;旨在通过风洞试验掌握木塔在人工植林遮挡下的风压与风荷载分布规律,探索利用人工植林技术减小木塔风荷载的可行性,为应县木塔及类似中式高耸古建筑的保护提供新思路。
1 风洞试验概况
1.1 应县木塔基本情况
应县木塔如图1所示。

图1 应县木塔Fig.1 Yingxian wooden pagoda
图1中,木塔实际高65.84 m,共9层,包括5个明层、4个平坐层(暗层)和屋顶[2-3]。明层与平坐层竖向交替建造,木塔底面面阔30 m,呈正八边形。由于服役过程中受到多种荷载作用,木塔第2层明层内外柱均已产生了一定的倾斜,如图2所示。

图2 木塔第2层明层内外柱倾斜Fig.2 Column inclination on the second floor of wooden pagoda
1.2 试验风场
应县木塔周边房屋较矮且较为稀少,所在区域属B类地貌,地面粗糙度指数为0.15[23];在模型高度为0.2 m处(即实际高度10 m高处)的风速取值为10 m/s。风洞测压试验在长沙理工大学大气边界风洞实验室高速试验段开展。该风洞实验室长21 m、宽4 m、高3 m,可试验风速为1~45 m/s,风洞试验示意图如图3所示,试验布置如图4所示。
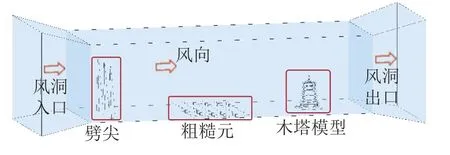
图3 风洞试验室示意图Fig.3 Diagram of wind tunnel test

图4 风洞试验布置Fig.4 Wind tunnel test setup
在风洞试验段入口处设置劈尖,并在试验段设置粗糙元(图4(a)),使风速与湍流度剖面达到规范要求。在风洞转盘试验区中心处测得风场平均风速与湍流度如图5所示。图5中,风速和湍流度剖面与理论值吻合良好,满足试验需求[24]。风洞试验参考点高度为1 m(相当于实际50 m高度)。von-Karman谱是风工程中最常用的风谱验证方法之一[25-26],因此,将参考点的脉动风速功率谱密度与von-Karman谱进行对比,如图6所示[27]。从图6中可以看出,吻合较为良好,满足要求。
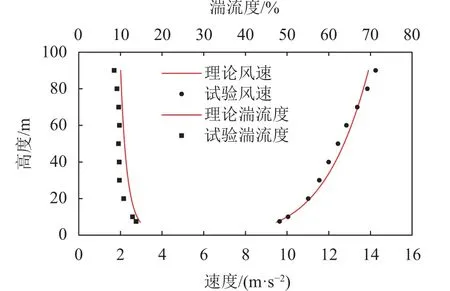
图5 平均风速与湍流度剖面Fig.5 Profile of mean wind speed and turbulence intensity
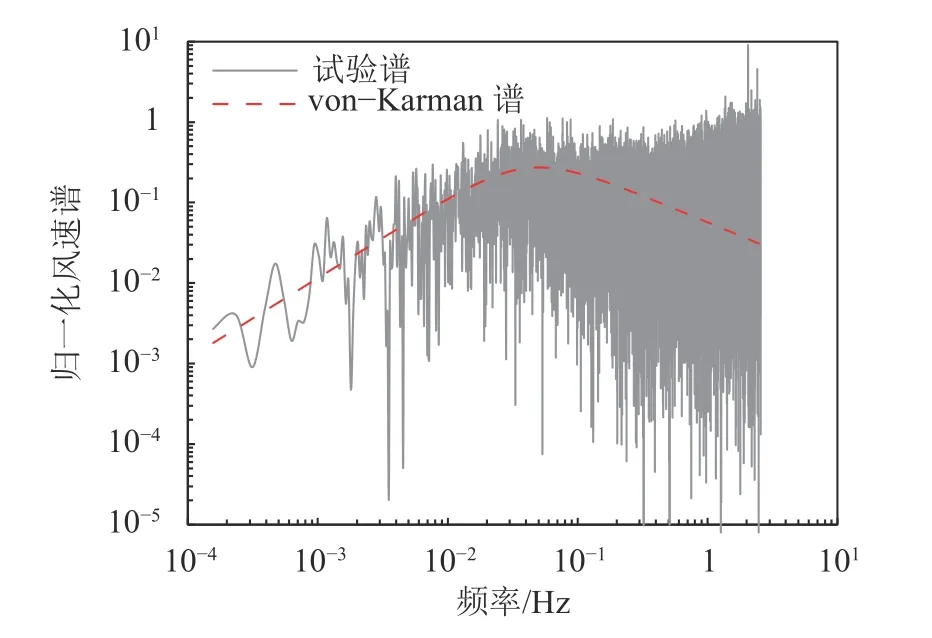
图6 1 m高处的风速功率谱密度与von-Karman谱对比[27]Fig.6 Comparison between velocity spectra at 1 m height and von-Karman spectra[27]
1.3 试验模型及测点布置
由于应县木塔高宽比较小,结构主体顺风向与横风向的风振响应较小,且本文主要目的是验证人工植林减少木塔风荷载的可行性,故采用刚性测压模型进行研究。基于风洞试验室条件,试验模型几何缩尺比为1∶50,模型高度为1.32 m,采用松木制作。试验缩尺模型精细地复刻了木塔外形结构特征,包括副阶廊柱、栏杆、斗拱、屋檐及宝顶。经计算,模型在风洞试验中的最大阻塞比为4.5%,满足规范5%的限值[24,28]。
因木塔平面为正八边形,且测压阀数量有限,选取木塔5个面(编号①~⑤)布置测压点,如图7所示。因本文重点关注植林树木对于木塔风荷载与风压的减缓程度,以及不同植林排布的影响,且木塔平面中心对称,因此风向角仅选取0°,即来流风向与①号面正交。植林树木均布置在木塔迎风面处。
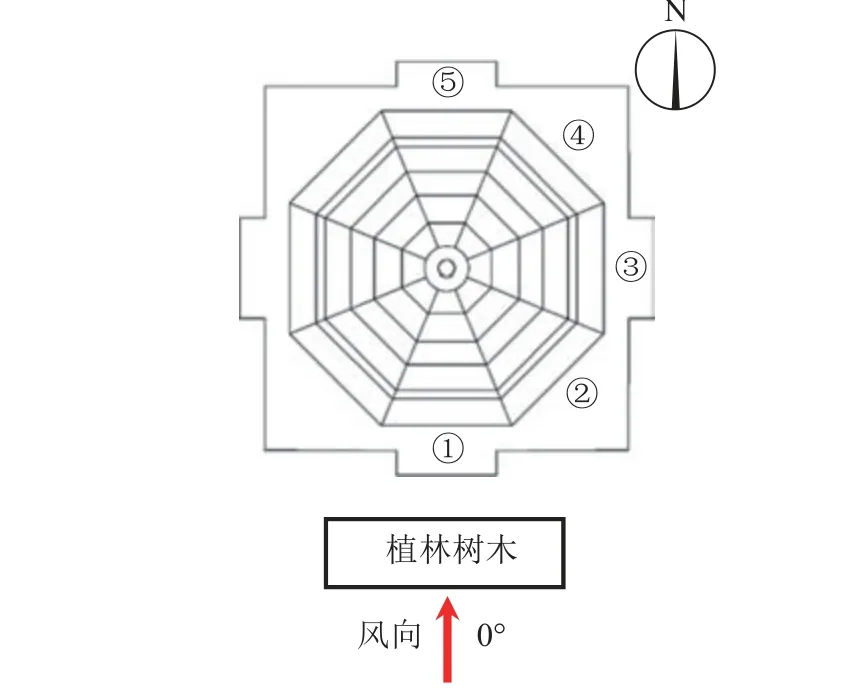
图7 木塔模型方位与风向示意图Fig.7 Schematic diagram of model orientation and wind direction
木塔模型中共布设了510对压力传感器,其中,①号面的压力测点布置如图8所示,其余面测点位置与数量与①号面类似,区别在于:①号面第1层墙面(明层)处中心测点(A2、A3、A6与A7)因门框突出而安装在门框上,其他测点面直接安装在墙面上。根据木塔外形特征,将每一个测点面沿高度方向分为11个测点区域,分别为:第1层墙面(A区域)、第1层副阶屋檐(B区域)、第2层平坐层屋檐(C区域)、第2层门窗(D区域)、第3层平坐层屋檐(E区域)、第3层门窗(F区域)、第4层平坐层屋檐(G区域)、第4层门窗(H区域)、第5层平坐层屋檐(I区域)、第5层门窗(J区域)、屋顶屋檐(K区域)。

图8 木塔风压测点布置Fig.8 Pressure tap distributions on wooden pagoda
第1层墙面区域(A区域)共布置12个测点,第2层至第5层的门窗区域(D、F、H和J区域)各布置13个测点,第1层副阶屋檐与第2层至第5层平坐层屋檐区域(B、C、E、G和I区域)各布置6个测点,屋顶屋檐区域(K区域)布置8个测点,每个测点面共有102个风压测点。需要说明的是,图8中,测点编号规则为“测点面编号+区域号+测点编号”。
1.4 树木模型
国内外已有学者提出了面向风洞试验的树木模型模拟制作方法,Hesp等[11]采用木质销栓与麻绳制作成树木,Queck等[29]采用圆柱形线框模拟灌木,沈炼等[22]采用塑料树木模型模拟街道行道树。然而,因本文选取的缩尺比较大,同时,为因地制宜,树木种类建议选择高大落叶乔木,如图9(a)所示,这使得树木模型外形尺寸较大,现有方法难以满足本文风洞试验的需求。

图9 树木原型与模型Fig.9 Prototype and model of plants
为此,本文采用一种基于遮蔽率的简化树木模拟方法。根据树木整体遮蔽率、实际树冠宽度及木板自身特性(抗风性与自重等),采用边长为6 mm的正方形桐木条模拟树干部分;选取尺寸为120 mm × 20 mm ×1 mm的木板模拟树冠部分,并沿高度每100 mm正交粘贴,如图9(b)所示。树木整体遮蔽率约为20%,这与无树叶的树木遮蔽率相近[30],同时也可模拟最不利的情况。
1.5 数据处理
风场的风速与湍流强度通过眼镜蛇探针进行测试,风压测试采用美国PSI DTC Initium型电子压力扫描阀进行。各测压孔均与结构表面垂直,所有连接测压孔与扫描阀的PVC软管均取同样长度,并在输出数据时进行畸变修正[31]。根据来流风速与几何缩尺比,为采集到准确数据,采样频率选定为200 Hz,采样时间为60 s,相当于原型结构约10 mins。规定风压数据中,正值为风压力,负值为风吸力。使用修正后的风压时程数据,通过式(1)可计算出每个测压点i的瞬时风压系数Cpi(t)为:
式中:Pi(t)为t时刻测点i的瞬时风压;ρ为空气密度,可取1.225 kg/m3;Vref为参考点(高度为1 m)风速。
2 树木布置工况
考虑3种植林布置条件,分别为树木高度H、树木距木塔距离D与树木布置宽度W,如图10所示。图10中,树木的列距与行距采用固定数值,分别为160与200 mm[32],树木布置于木塔的正前方(图4(c))。树木布置工见表1。表1中:工况1、2、3和4考虑树木高度变化,其树木高度分别为200、300、400及500 mm,相当于实际高度10、15、20及25 m;工况5、6和7考虑树林距木塔距离的变化,其距离木塔分别为600、800及1 000 mm,这里距离指的是木塔中心至第1排树木的距离;工况3、6及8考虑树木布置宽度的变化,其布置宽度分别为1 120、1 760及2 400 mm。
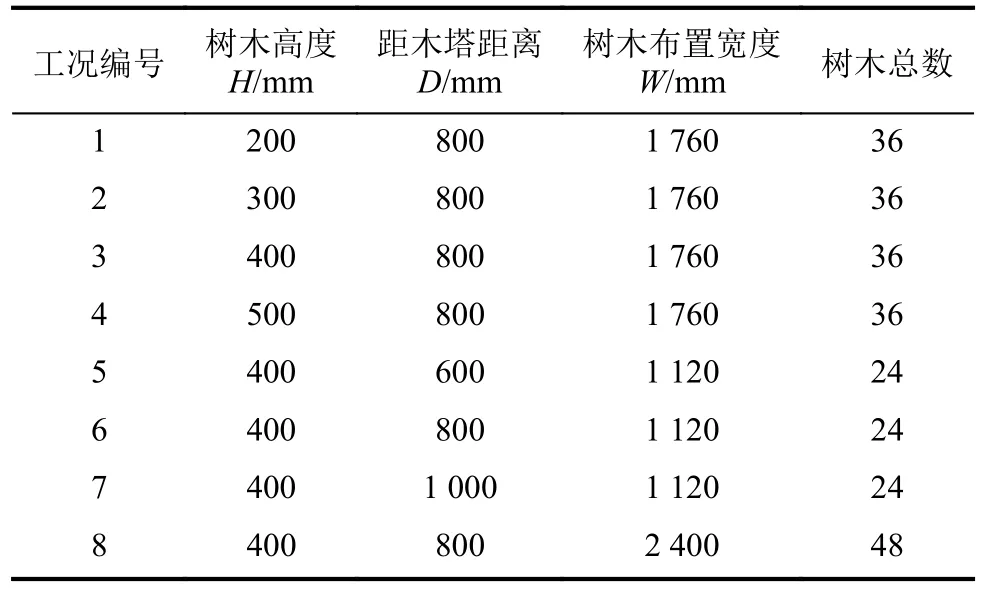
表1 树木布置工况Tab.1 Plant arrangement conditions
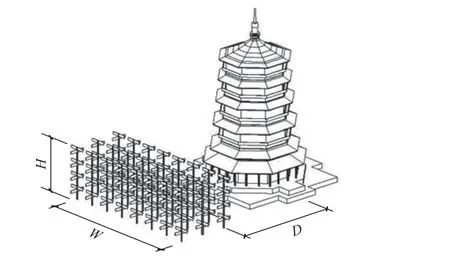
图10 树木布置工况示意图Fig.10 Schematic diagram of tree arrangement conditions
3 木塔风压分布
3.1 无树木
木塔每个测点的风压系数平均值Cpmean可通过式(1)对瞬时风压系数进行计算。木塔在0°风向角作用下的平均风压系数云图如图11[33]所示。从图11可以看出:①号面除屋顶外均受风压力,最大风压系数出现在木塔迎风面中偏上部,其数值为+0.700;第1~4层平坐层屋檐均受风压力,数值与明层风压相近,说明来流风未发生分离;在屋顶处,风压力转为风吸力,其最大值为-0.710;①号面的风压分布与现代建筑较为相似。在②号面上,绕流木塔的风会引起木塔表面风压系数由正转为负,且转变速度较快;靠近风来流方向为正,远离来流方向为负,所以②号面中心线位置风压系数接近0;在②号面屋顶处,风压系数为负,最大可达-1.090。整个③号面均受较大风吸力,平均风压系数超过-0.600,其中最大值出现在A区域与K区域,分别为-1.243与-1.220,这是因为A区域的副阶游廊流通截面小,导致风速加快,风压增大,同时风在K区域分离产生较大的风吸力。在④与⑤号面上,木塔主要受风吸力,且风压变化较小,除屋顶外的风压平均值为-0.600;最大风吸力出现在屋顶区域,为-0.959。
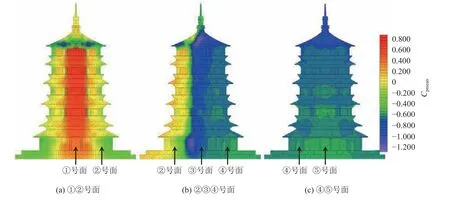
图11 无树木工况下各面在 0°风向角下平均风压系数等值线[33]Fig.11 Contour plots of mean pressure coefficients of the isolated pagoda at wind direction of 0°[33]
3.2 有树木
不同树木工况下木塔风压分布趋势相似,选取最具代表性的工况3进行分析。图12为木塔在有树木(工况3)下0°风向角的平均风压系数。
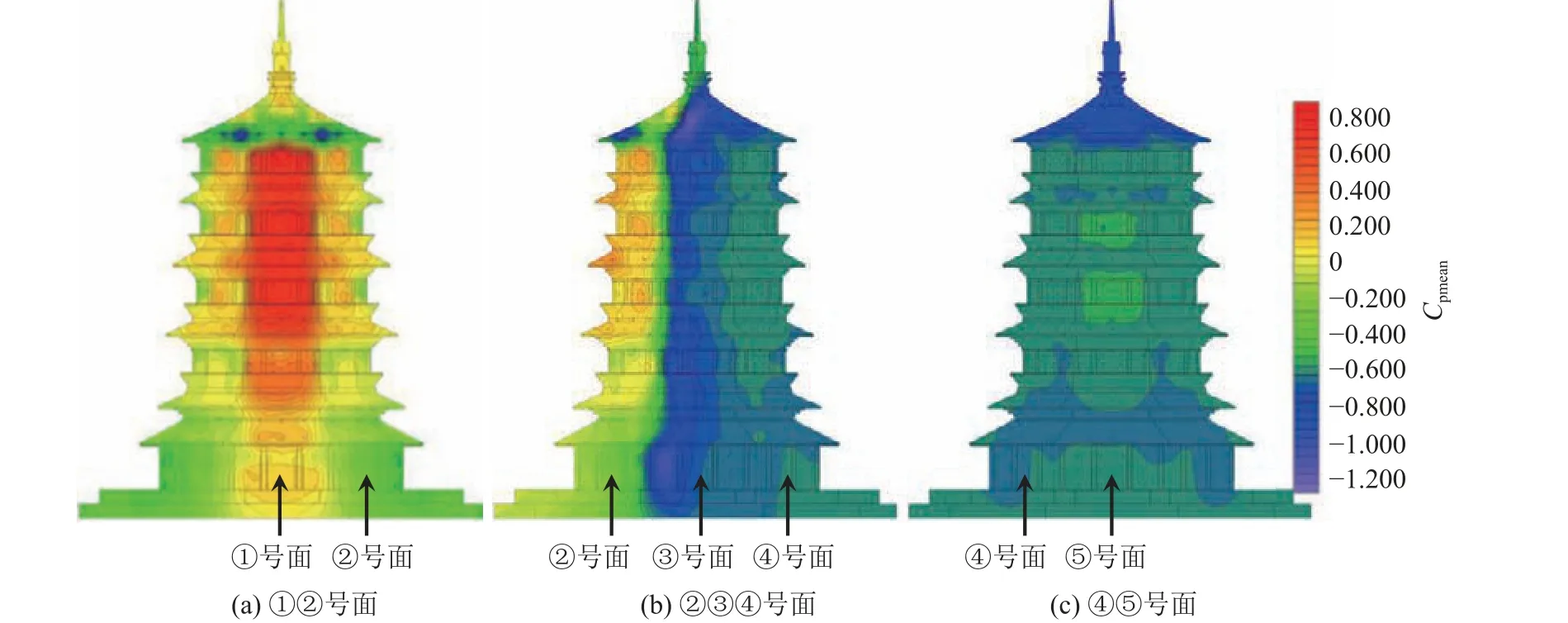
图12 有树木工况下(工况3)各面在 0°风向角下平均风压系数等值线Fig.12 Contour plots of mean pressure coefficients of pagoda under the tree blocking (Case3) at wind direction of 0°
由图12可见:在①号面上,风压系数绝对值在树木遮挡区域内有大幅度减小,整体减小幅度可达55.5%;当高于遮挡区域时,风压系数逐渐增大,当高于500 mm时,有树木工况木塔风压系数绝对值略大于无树木工况下木塔风压系数,但总的来说,树木在迎风面具有较好的遮挡作用效果。在②号面上,遮挡区域内各工况均呈现风吸力,且风吸力绝对值较无树木工况大;树木越高,风吸力越大,但风压系数绝对值小于0.4。在③号面上,有树木工况风压系数绝对值整体小于无树木工况的风压系数;当木塔高度大于500 mm时,有树木遮挡下的风压系数绝对值比无树木工况小很多,最大可减小15.7%。值得注意的是,尽管树木高度比木塔低,但树木依然对屋顶及木塔高层区域的风压分布产生影响。在④与⑤号面上,有树木工况下木塔风压系数绝对值在150 mm高度以下略大于无树木工况;当高度大于150 mm时,木塔风压系数小于无树木工况,最大可减小17.7%。
4 风荷载作用及影响因素分析
4.1 计算方法
风荷载主要包括风层间力与层倾覆弯矩,各层累加可得风基底剪力与风基底倾覆弯矩[31]。风层间力与倾覆弯矩可通过模型实际风压与高度进行计算,风荷载计算区域与测点划分区域相同,如图8所示。测点的风力与风倾覆弯矩可通过式(2)与(3)计算:
式中,Fji与Mji分别为在j区域的第i测点的风层间力与风倾覆弯矩,Pimean为i测点的平均风压系数,Ai为i测点的所属面积,α与β分别为i测点风压力与水平面和竖直面的夹角,hi为测点i的高度。需要注意的是,本文风倾覆弯矩为水平风压引起的弯矩,竖向弯矩分量因对结构倾覆具有减缓作用而忽略。
第j区域的层间力Fj与层倾覆弯矩Mj分别为:
式中,n为区域j的风压测点数量。将各区域风层间力与层倾覆弯矩相加,则可得到风荷载基底剪力与基底弯矩。
为评估植林树木遮挡后的木塔风荷载减缓效果,分别定义基底剪力与基底弯矩的减小率分别为:
式中,F与M分别为人工植林的木塔风基底剪力与弯矩,F(0)与M(0)为没有树木遮挡情况下的基底剪力与基底弯矩。
4.2 影响因素
4.2.1 树木高度影响
采用式(2)~(5)计算不同树木高度下木塔风层间力与风层倾覆弯矩,结果如图13所示。由图13可见,木塔各明层风层间力比平坐层层间力大。树木越高,遮挡区域越大,区域内风层间力越小。如B区域内,层间力从大到小依次为无树木工况、工况1(树高200 mm)、工况2(树高300 mm)、工况3(树高400 mm)与工况4(树高500 mm)。当超过树高遮挡范围时,工况1与2层间力比无树木遮挡情况下的层间力大,如:工况1在C与D区域的层间力,但增幅仅为3.5%左右;工况4下的E区域出现最大层间力减小率,其值可达37.9%,同时D区域层间力减小率也可达29.7%,说明树木高度增加可有效减小木塔风荷载,特别是对木塔第2层明层风荷载。层倾覆弯矩随高度增加而增加;同时,因低层高度较小,层倾覆弯矩减小效果不明显。
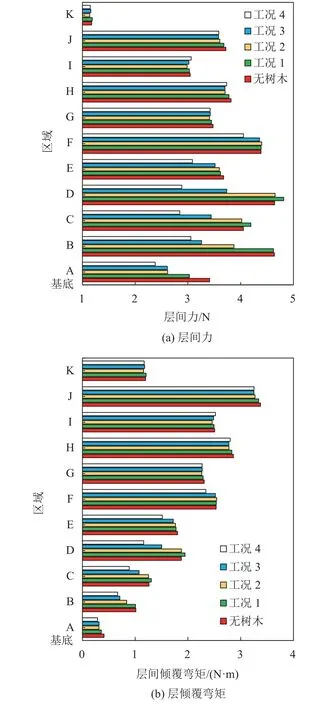
图13 不同树木高度下风荷载的分布Fig.13 Wind load distribution of pagoda with various plant heights
分别采用式(6)与(7)计算基底剪力与弯矩的减小率如图14所示。由图14可见:随着树木的增高,基底剪力与弯矩减小率有较大幅度增加,最大减小率分别达到16.9%与10.7%,说明树木高度的增加可有效减小基底剪力与弯矩,减缓风荷载对于木塔的作用。同时,当树木增高时,基底剪力与弯矩减小率会有较大幅度增加,说明当采用人工植林技术减缓风荷载时,应尽量选取高大树木;当树木高度低于200 mm时(实际为10 m高),树木对木塔风荷载的影响可忽略。
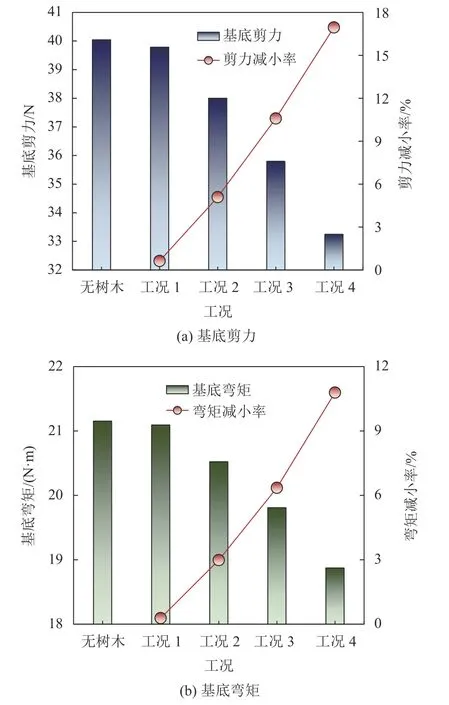
图14 不同树木高度下风荷载基底剪力与基底弯矩及减小率Fig.14 Wind base shear force and moment and reduction ratio of pagoda with various plant heights
4.2.2 树木距木塔距离的影响
不同树木与木塔距离下木塔的风荷载分布情况如图15所示。由图15可见,在遮挡高度范围内,当树木距离木塔越近,遮挡效果最好,层间力由小到大分别为工况5(距离600 mm)、工况6(距离800 mm)和工况7(距离1 000 mm)。在区域D,工况5的层间力比工况7的层间力大6.5%;而在高层区域上,工况5层间力比工况7小,但整体变化幅度较小。在区域B,各工况出现最大层间力减小率,分别为30.1%(工况5)、28.6%(工况6)与27.7%(工况7);层倾覆弯矩与层间力相似,最大层间倾覆弯矩减小率分别为30.1%、28.8%与28.1%,各工况相差较小。
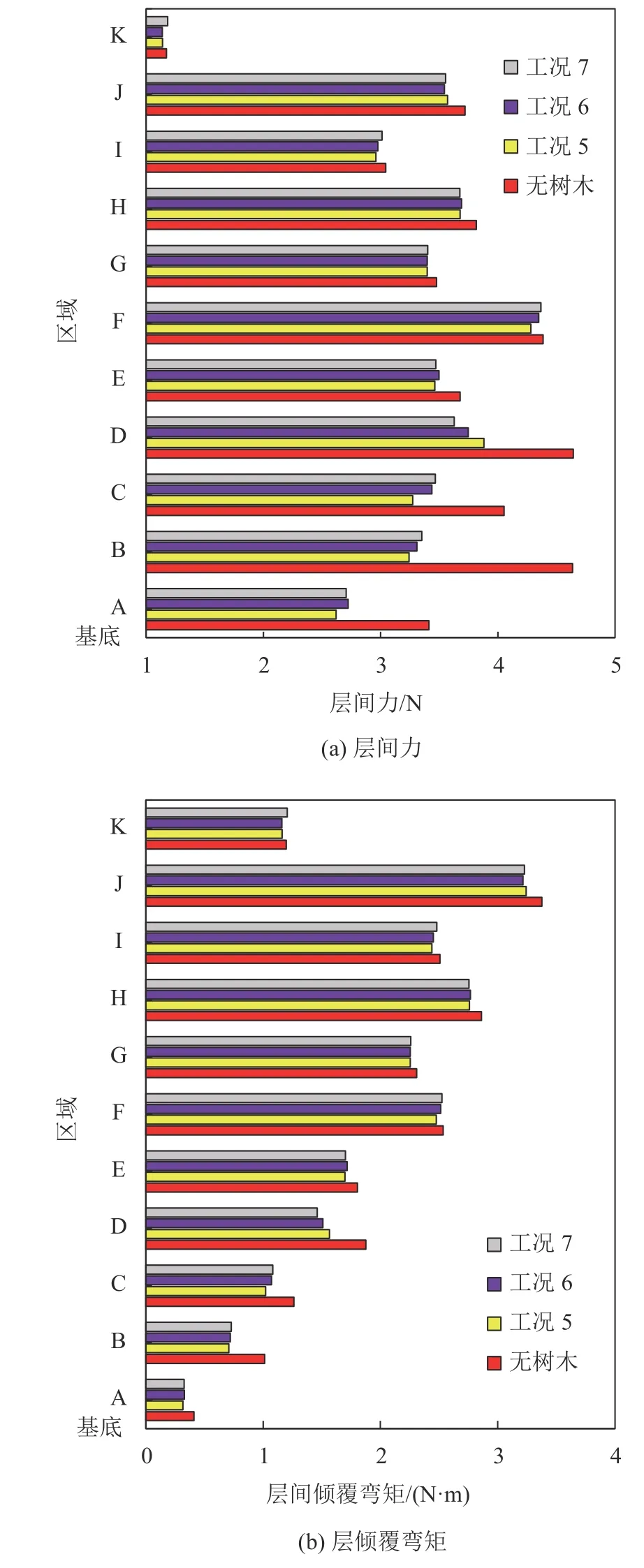
图15 距木塔不同距离下风荷载的分布Fig.15 Wind load distribution of pagoda with various distances from the pagoda
计算不同树木与木塔距离下的基底剪力与弯矩的减小率如图16所示。由图16可见,树木离木塔越近,基底剪力与弯矩减小率越大,其最大减小率可达11.3%与7.1%。结果表明,将树木布置在离木塔尽量近的区域,会较好地减小风荷载。
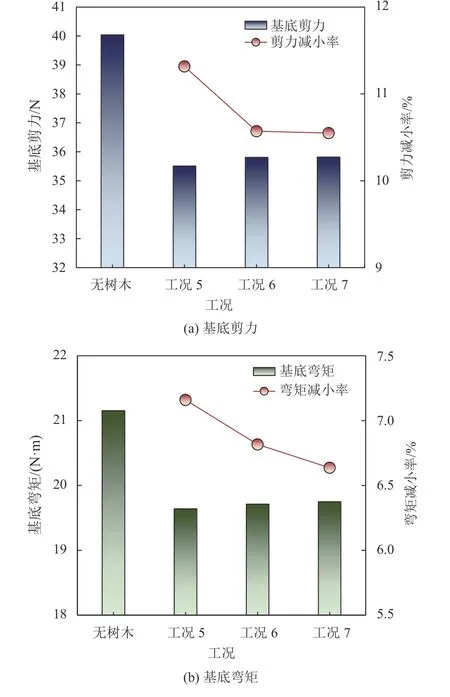
图16 距木塔不同距离下风荷载基底剪力与弯矩及减小率Fig.16 Wind base shear force and moment and reduction ratio of pagoda with various distances from the pagoda
4.2.3 树木布置宽度的影响
不同树木布置宽度下木塔的风荷载分布情况如图17所示。由图17可见,在遮挡区域内(A、B与C区域),层间力由大到小依次为工况6(1 120 mm)、工况3(1 760 mm)与工况8(2 400 mm),但相差较小。值得注意的是,当高于遮挡区域时,工况8的风层间力比工况6大,主要原因在于,较宽的树木布置会使树木离风洞试验边界过近,进而使得风流速增大,造成木塔风荷载增加。在区域B,工况6、3及8出现最大层间力减小率,分别为28.6%、29.7%与30.1%;层倾覆弯矩与层间力相似,由于在遮挡区域内不同工况层间力变化较小,且高度较矮,所以计算出的弯矩差别很小。在高于遮挡区域高度,特别是在H区域(第4层明层)与J区域(第5层明层),工况8倾覆弯矩比工况6与3大,这与层间力趋势相符。
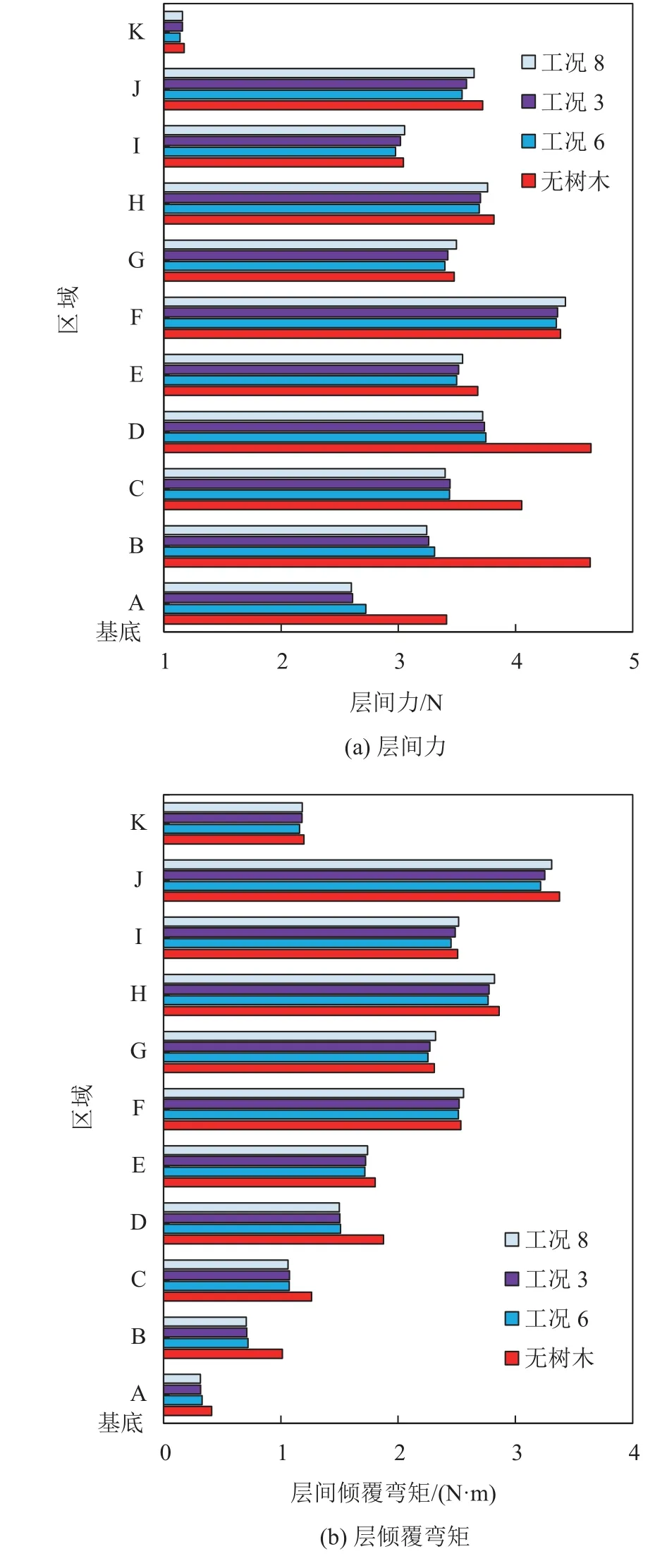
图17 不同树木布置宽度下风荷载的分布Fig.17 Wind load distribution of pagoda with various plant widths
不同树木布置宽度下基底剪力与弯矩计算结果如图18所示。由图18可见,当树木布置宽度增大时,基底剪力与弯矩有所增大,减小率降低。这可能是由于树木排布过宽导致风流速变大,产生了较大风压力。若仅从遮挡区域内的减缓效果来看,树木排布越宽,减缓风荷载效果越好。
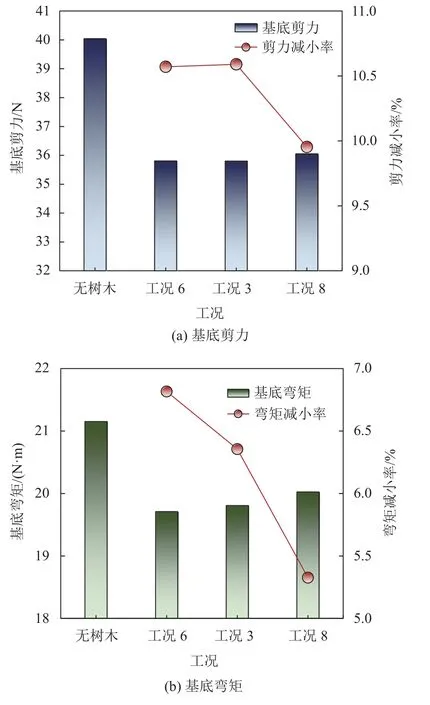
图18 不同树木布置宽度下风荷载基底剪力与弯矩及减小率Fig.18 Wind base shear force and moment and reduction ratio of pagoda with various plant widths
5 结 论
本文开展了基于人工植林的削减高耸古木塔风荷载作用的风洞试验研究,提出了适用于大缩尺比高大乔木的风洞试验模型制作方法,考察了木塔表面在有无树木遮挡下的表面风压分布,计算了木塔风层间力与层倾覆弯矩,并分析了木塔基底剪力与弯矩的减小率。研究结论如下:
高耸古木塔风压分布规律与现代建筑完全不同,除迎风面受到风压力外,其余各面与屋顶均受到较大的风吸力。采用木条与木板可较好地模拟大缩尺比的高大乔木模型,通过调整木板数量与位置改变树木高度与遮蔽率。
树木的遮挡作用会很大程度影响木塔所受风荷载,最大层间力减小率可达37.9%。树木越高,遮挡范围越大,风荷载减小率越大,最大基底剪力与弯矩减小率可达17.0%与10.8%。而距木塔越近,风荷载减少率有小幅增加。
树木布置宽度越宽,在遮挡区域内,木塔风荷载有小幅降低。经现场调研,木塔西侧为城市公园,适宜布置植林树木来减缓来自西南主导风向的风荷载作用。综合而言,当采用人工植林缓解木塔风荷载时,应选用高度较高的树木,以尽量宽地宽度布置在距木塔西南侧的较近区域。
本文开展了高耸古木塔在不同植林树木高度、距木塔距离与布置宽度下的风洞试验研究,旨在为削减木塔风荷载作用提供新的思路。实际植林树木的单体与整体遮蔽率比风洞试验高,对木塔有更好的遮挡作用。另外,本方法可与结构加固增强相结合,同时从减小外荷载与增加结构抗力两方面缓解高耸古木塔的风致损伤。
