加设自复位支撑冷弯型钢龙骨剪力墙滞回性能研究*

2023-05-25马园泽符宇欣赵金友张文莹余少乐

工业建筑 2023年1期

马园泽符宇欣陈亮赵金友张文莹余少乐

(1.北京工业大学工程抗震与结构诊治北京市重点试验室, 北京 100124; 2.上海天华建筑设计有限公司, 上海 200235; 3.上海应用技术大学城市建设与安全工程学院, 上海 201418; 4.中国建筑第八工程局有限公司, 上海 200122)

在冷弯型钢结构中复合墙体是主要的结构单元,承担结构的水平和竖向荷载。复合墙体由钢龙骨、结构外墙覆面板(定向结构刨花板、带肋波纹钢板等)和内墙覆面板(石膏板等)通过自攻螺钉连接而成。[1-2]覆面材料包括定向结构刨花板、波纹钢板覆面板及平钢板等,定向结构刨花板是可燃材料,防火性能较差;平钢板可以克服可燃性,但是抗剪强度较低,剪切屈曲时会产生很大的平面外变形;采用波纹钢板覆面板可以改善以上两种面板的缺点。冷弯型波纹钢板覆面板钢龙骨剪力墙的初始刚度和承载能力较好,但是延性不高。[3]为提高其延性,文献[4-5]介绍了对开狭缝墙体的研究,得出虽然开设狭缝能提高其延性但是承载力会被削弱的结论。闫维明等为了提高冷弯型钢组合墙体的延性和变形能力,在墙体里放置延时保护支撑,结果表明安装支撑不但可有效提高墙体的延性、极限变形能力及耗能能力,而且可以延缓刚度退化并降低峰值点后承载力损失。[6]同年,闫维明等为改善冷弯型钢组合墙体在低周反复加载试验中滞回曲线“捏拢”现象和耗能能力差的缺点,在墙体里放置铅阻尼器,结果表明安装铅阻尼器的墙体破坏模式得到优化,延性和耗能能力也提高了0.3～2.4倍。[7]虽然加设耗能支撑剪力墙的延性及耗能能力较未加设支撑墙体有明显提升,但此类结构在震后不可修复,仍会造成较高的经济损失。如何能减小结构在地震中损伤,同时震后可复位是一个新的思路。

可复位结构主要包括摇摆结构、自复位框架结构和加设自复位支撑。在发生地震时,摇摆结构变形不协调,最终导致结构不同部分之间的破坏问题;而自复位框架结构存在震后不易更换损坏的自复位构件的缺点;而加设自复位耗能支撑的结构在抗震中不但能够消耗大量地震能量,令破坏集中在支撑上,而且方便更换,震后仅更换支撑即可,结构稍加修复或者不加修复仍可继续使用的效果。自复位耗能支撑大部分通过内、外管的相对位移来消耗地震能量,帮助结构复位。[8-10]支撑的工作阶段分为:1)开始加载至内、外管即将发生相对位移;2)内、外管发生相对位移至开始卸载;3)开始卸载至支撑开始复位;4)复位阶段。自复位构件按材料可分为:碟簧、形状记忆合金、预应力钢筋或钢绞线、纤维筋;耗能构件按工作机制可分为:摩擦耗能、黏滞阻尼耗能、金属屈服耗能。徐龙河等提出了一种由组合碟簧和摩擦耗能装置共同组成的新型装配式自复位耗能支撑,核心杆与外管上的挡块使碟簧均处于受压状态,因提供恢复力使支撑复位,核心杆与外管之间允许发生相对滑动,此时摩擦板耗散能量;进行了往复加载试验,验证了结构的可行性;并提出了一种加支撑的钢板墙并进行数值模拟,得出加设自复位耗能支撑能提高剪力墙的极限承载力和耗能能力,减小墙体的残余变形。[11-12]碟簧可以预压,具有压缩行程较大、可以在较大的位移中提供稳定的复位能力的优点。摩擦耗能在低周往复加载中提供稳定的耗能效果,若是采用金属屈服耗能会造成一次性永久变形,不适合在往复加载中使用。通过将自复位耗能支撑引入到冷弯型钢龙骨剪力墙结构体系当中,减小钢龙骨剪力墙的延性损伤及残余变形。

基于上述研究,提出了一种用碟簧作为自复位构件,采用摩擦进行耗能的支撑,并将其斜对角放入钢剪力墙中。在介绍加设支撑的剪力墙的构造和支撑的工作原理的基础上,将进行剪力墙的精细化数值模拟分析,通过应力分布图和滞回曲线,对有、无加设支撑墙体的承载力、延性、耗能能力和残余变形进行比较,并对自复位耗能支撑进行变参分析,分析碟簧刚度、预压力和摩擦力对抗震性能的影响。

1 加设自复位耗能支撑冷弯型钢龙骨剪力墙体系

1.1 剪力墙构造

加设自复位耗能支撑冷弯型钢龙骨剪力墙由典型的冷弯型钢龙骨剪力墙及自复位耗能支撑组成,自复位耗能支撑主要包括自复位耗能构件、连接杆、花篮螺栓和杆端轴承四个部分。两个自复位耗能支撑沿墙体对角线布置,并通过杆端轴承与剪力墙的抗拔件相连,使用杆端轴承可避免墙体和支撑连接处发生挤压破坏。连接杆通过花篮螺栓进行装配,拆卸简单,方便震后更换受损的支撑。加设自复位耗能支撑剪力墙构造如图1所示。

图1 冷弯型钢墙体骨架和支撑安装示意Fig.1 A installation diagram of cold-formed steel wall frameworks and braces

1.2 自复位耗能构件构造

自复位耗能构件主要包括支撑外筒、支撑内杆、工型钢、外筒上挡板、摩擦板、碟簧和花篮螺栓。支撑外筒上安装外筒上挡板和下挡板,通过外筒和内杆之间的相互运动,碟簧被压缩,摩擦板与外筒之间产生摩擦力,实现自复位和耗能效果。在碟簧上施加的预压力和碟簧被压缩后产生的恢复力是剪力墙的复位力,同时通过改变摩擦板上螺栓扭矩的大小来改变支撑提供的摩擦力,提供的这部分摩擦力能耗散部分剪力墙的地震能量,如图2所示。

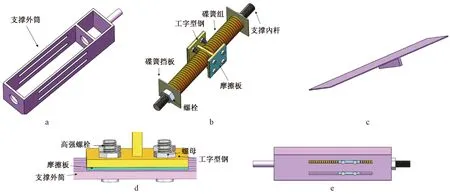
a—支撑外筒; b—支撑内杆; c—支撑外筒上、下挡板; d—摩擦耗能装置; e—支撑组装。图2 自复位耗能构件示意Fig.2 Schematic diagrams of self-centering energy-dissipation members

1.3 支撑工作原理

支撑形式采用碟簧作为自复位构件,是因为碟簧片可以进行预压,且压缩行程较大,可以在较大的位移中提供稳定的复位能力。采用摩擦耗能,可以实现低周往复加载中的稳定耗能效果。若采用金属屈服耗能会造成一次性永久变形,不适合在往复加载中使用。

受拉激活前状态:自复位耗能支撑斜向布置在剪力墙的抗拔件上,此时支撑的启动力为摩擦力和预压力之和,碟簧并没有被压缩,摩擦也为静摩擦,预压力和摩擦力处于自平衡状态,内杆与外筒的相对位移可忽略不计,如图3a所示。

a—受拉激活前状态;b—受拉激活后状态;c—受压激活前状态;d—受压激活后状态。图3 支撑加卸载状态Fig.3 Loading and unloading states of braces

受拉激活后状态:当墙体受到水平作用力时,自复位耗能支撑的内杆和外筒开始出现相对位移,支撑由原来的静摩擦变成动摩擦,帮助剪力墙消耗地震能量。在克服碟簧的预压力后,碟簧挡板和外筒分别挤压碟簧,为支撑和墙体提供正向复位力。如图3b所示。

受压激活前状态:当支撑卸载时,支撑运动方向发生改变,摩擦由动摩擦改为反方向的静摩擦,支撑承载力减小,此时碟簧又恢复到其初始位置,碟簧不受力。如图3c所示。

受压激活后状态:继续发生相对位移,此时摩擦由静摩擦变为动摩擦,碟簧也开始被压缩,且当碟簧提供的预压力能够完全克服耗能装置的静摩擦时,支撑才能完全自复位,如图3d所示。

自复位耗能支撑可以在冷弯型钢龙骨剪力墙受到拉压时提供一个侧向刚度,提高墙体结构的初始刚度。通过耗能构件的相对运动,来消耗地震产生的能量。通过碟簧的预压力和自恢复力来减小结构的损伤,不会给结构带来较大的残余变形。

2 自复位支撑复合墙体抗剪性能模型介绍

为比较自复位耗能支撑剪力墙在循环往复荷载下的滞回性能,共计对11个足尺模型进行数值模拟,试件详情见表1。对试件A-1[12]先进行有限元模型的验证,试件B-1在试件A-1的基础上加设自复位耗能支撑,对比有、无加设支撑的抗震效果。再在加设支撑(试件B-1)的基础上,改变自复位耗能支撑的参数,其中,C、D、E组分别考虑预压力、摩擦力和碟簧刚度对墙体抗震性能的影响。

表1 自复位耗能支撑试件详细情况Table 1 Details of self-centering energy-dissipation braces

3 钢龙骨剪力墙的精细化数值模拟

3.1 不加设支撑的钢龙骨剪力墙的数值模型验证

3.1.1墙体模拟介绍

对足尺双覆面板钢龙骨剪力墙进行低周反复了抗剪承载力试验[12],试验装置如图4所示。墙体高3 000 mm,宽为2 400 mm。墙体两侧面板为12 mm厚度的石膏板和12 mm厚度的定向结构刨花板(OSB板)。复合墙体试件的钢龙骨立柱均采用开口卷边槽形冷弯型钢,为Q345钢材,Q345 钢龙骨的截面为C90×35×10.3×0.8,顶轨、底轨为冷弯U型钢,规格 U92×35×0.8。钢龙骨墙体的支撑采用柔性支撑。墙体试件的钢龙骨示意如图5所示。覆面板与龙骨骨架采用自攻螺钉连接,墙体周边及接缝处螺钉间距为150 mm,内部为300 mm。

图4 试验装置[12]Fig.4 Test devices

图5 钢龙骨示意 mmFig.5 The schematic diagram of steel keels

试件的破坏现象为立柱和面板连接处螺钉出现损伤,有的拔脱或者深陷板中,石膏板在接缝处发生局部破坏,角部应力集中;OSB板的刚度较大,在接缝处发生面板错动,应力集中现象不明显。[12]

3.1.2龙骨构件和覆面板的数值模拟

墙体龙骨和覆面板均应先定义截面材料,根据材性试验结果[12],龙骨构件屈服强度为429.4 MPa,弹性模量为2.03×105MPa。墙体的破坏主要为螺钉拔脱破坏,塑性变形发生在螺钉处,面板则可以不用考虑塑性变形,假设OSB板和石膏板为弹性材料,OSB板材的弹性模量E=3 500 MPa,泊松比ν=0.3。[13]纸面石膏板的弹性模量E=1 587 MPa,泊松比ν=0.23。[14]

龙骨构件采用框架截面中的Cold Formed C定义,边立柱的截面定义为C90×35×10.3×1.6,中间立柱定义为C90×35×10.3×0.8,上下导轨和撑杆定义为U92×35×0.8 mm。覆面板采用薄壳面板模拟,定义厚度为12 mm。

3.1.3自攻螺钉连接的数值模拟

根据自攻螺钉的试验数据[15]得到其骨架曲线和滞回曲线。采用改进的“Foschi”指数型函数得出自攻螺钉的表达式,如式(1)所示,改进的“Foschi”指数型函数只在峰值处有一个拐点,更能准确模拟自攻螺钉的骨架曲线,上升段是指数型曲线,下降段为斜向线段。改进的“Foschi”指数型骨架曲线模型如图6所示。该骨架曲线须要确定6个参数,分别为k1、k2、k3、F0、δm、δu。k1为曲线的初始切线刚度,k2为强化段切线刚度,k3为下降段刚度,F0为强化段切线与y轴的交点,δm为荷载到达峰值时的变形,δu为荷载到达破坏荷载时的变形。改进的“Foschi”指数型函数与试验中螺钉的骨架曲线吻合,钢龙骨与 OSB 板自攻螺钉连接拟合曲线与试验曲线对照,如图7a所示,钢龙骨与纸面石膏板自攻螺钉连接拟合曲线与试验曲线对照,如图7b所示。骨架曲线须要确定的6个参数如表2所示。

表2 改进的“Foschi”指数型骨架曲线计算的模型控制参数Table 2 Control parameters of models calculated by the improved “Foschi” exponential skeleton curve

图6 改进的“Foschi”指数型骨架曲线模型Fig.6 The improved “Foschi” exponential skeleton curve model

a—钢龙骨与 OSB 板自攻螺钉连接;b—钢龙骨与纸面石膏板自攻螺钉连接。---test 1[15]; ……test 2[15]; --·-·test 3[15]; ——模拟。图7 龙骨与面板自攻螺钉连接拟合骨架曲线与试验骨架曲线对照Fig.7 Comparisons between fitting skeleton curves and test skeleton curves for structures of keels and panels connected with screws

(1)

式中:Fm为峰值荷载。

采用 Pivot 定点指向型滞回模型来模拟螺钉连接的滞回规则。一个Pivot连接单元(多线段塑性连接单元)可模拟三个转动和三个平动方向。Pivot 模型是在观察构件加载、卸载、反向加载和反向卸载时的滞回曲线分别趋向于某些特殊点(Pivot点)的基础上提出的。如图8所示,在 Pivot 模型定义的滞回规则中,OP4和OP2分别为构件正向和反向加载时的弹性加载线,水平位移轴正、反向弹性加载线(非竖向荷载轴)将平面分为Q1、Q2、Q3、Q44个象限,同时定义P1、P2、P3、P4、PP2、PP4为Pivot点。在Q1象限时,1指向P1为加载方向,背离P1则为卸载方向,在Q3象限时定理相同;在Q2象限时,2指向PP2为加载方向,背离P2则为卸载方向,在Q4象限时定理相同。

图8 Pivot的滞回规则Fig.8 Hysteresis rules of in the Pivot model

定点指向型滞回模型如图9所示,所有Pivot点均在恢复力曲线的弹性加载线上,在加载方向的反向OP1与卸载方向(3—4方向)交点为P1,对应的纵坐标用α1Py1表示。在反向弹性加载方向OP2与卸载方向(4—5方向)交点为PP2,对应的纵坐标用β2Py2表示。在加载方向的反向OP3与卸载方向(7—8方向)交点为P3,对应的纵坐标用α2Py2表示。在正向弹性加载方向OP4与卸载方向(12—1方向)交点为PP4,对应的纵坐标用β1Py1表示。

αi、βi为捏拢和卸载的控制点,i=1,2。图9 Pivot滞回模型Fig.9 The Pivot hysteretic model

通过试验数据整理得出:αOSB=18.73,βOSB=0.39;α石膏=27.48,β石膏=0.42。由于正反向加载时各特征值相差不大,故α1=α2,β1=β2。参数η是弹性加载线的旋转角度,用于 Pivot 模型的修正,一般不予考虑,故取η=0。钢龙骨OSB板自攻螺钉连接模拟结果与试验对照如图10a所示,钢龙骨纸面石膏板自攻螺钉连接模拟结果与试验对照如图10b所示。

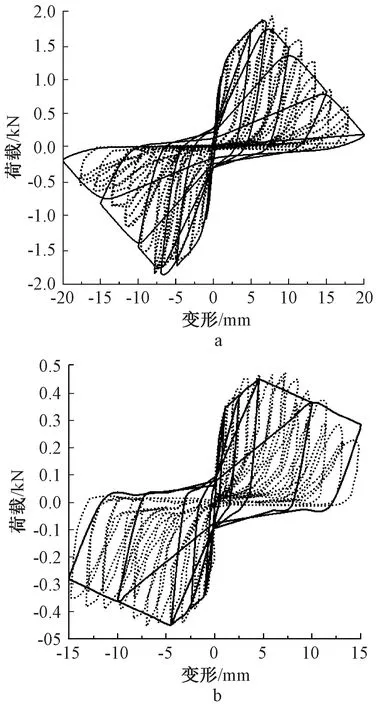
a—钢龙骨与 OSB 板自攻螺钉连接;b—钢龙骨与纸面石膏板自攻螺钉连接。……试验曲线[15]; ——模拟曲线。图10 龙骨与面板自攻螺钉连接拟合滞回曲线与试验滞回曲线对照Fig.10 Comparisons between fitting hysteretic curves and test hysteretic curves for structures of keels and panels connected with screws

采用SAP2000建立了两结点的螺钉连接数值模型,模型中的两个结点采用多线段塑性连接单元,可模拟单向拉压变形。输入表2中的骨架曲线控制参数,使用α1、α2、β1、β2和η,模拟滞回曲线,共同组成自攻螺钉的恢复力模型。

采用双连接模型模拟自攻螺钉连接面板与龙骨的连接,如图11所示。采用不相互影响的双连接,分别是连接墙高和墙宽方向,因为墙体剪力主要在这两个方向。横向荷载作用下,边柱和中柱主要承担的剪力近似平行于边立柱贴合的板边方向,而位于面板上下端的导轨主要承受的剪力方向近似垂直于导轨贴合的板边方向。

图11 双连接模型Fig.11 The double-connection model

3.1.4边界条件设置

数值模型中采用铰接模拟龙骨构件间的自攻螺钉连接。在数值模型中,将上下导梁作为刚性构件考虑,并约束导梁各节点沿垂直于墙面方向的平动以及绕其轴线的转动。模型中约束立柱绕其轴线的转动。

3.1.5模型验证

采用SAP2000模拟的低周往复试验[12],得到的滞回曲线与试验作对比,其弹性刚度、峰值荷载、峰值位移、延性和残余变形均可较好地拟合,如图12和表3所示。因此,SAP2000可以进行冷弯钢龙骨剪力墙的模拟。

表3 不加支撑的剪力墙滞回曲线数据对比Table 3 Comparisons of hysteretic curve data of shear walls without braces

……试验曲线[15]; ——模拟曲线。图12 水平荷载与侧向位移的模拟试验对比Fig.12 Comparisons between simulation test and simulation results of horizontal loads and lateral displacement

3.2 加设支撑的钢龙骨剪力墙的数值模型建立

钢龙骨剪力墙的建模模拟方法与3.1节相同。由于在SAP2000中没有现成的自复位耗能支撑模型的连接单元,且主要考虑到支撑的串、并联关系(组合碟簧与耗能装置为并联,在其并联的基础上与支撑的内杆外筒进行串联),故采用SAP2000连接单元中的线性连接单元来模拟支撑的内杆外筒,多段线弹性连接单元来模拟组合碟簧,多段线塑性连接单元来模拟摩擦装置。

自复位耗能支撑的SAP2000模型示意如图13所示,左侧示意图表示内杆外筒的线性连接单元的刚度为K1,L,中间上面示意图表示碟簧的多线性弹性连接单元,第一刚度为K1,ML,预压力为P0,第二刚度为K2,ML;中间下面示意图表示摩擦耗能装置的多线段塑性连接单元,用随动硬化模型模拟,第一刚度为K1,MP,第二刚度为K2,MP,其值为0,摩擦力用F表示。用三种连接单元模拟出旗形滞回曲线,如右侧示意图所示,曲线当中的第一刚度为K1;第二刚度为K2;激活力为Pa,耗能能力为2F。计算式如式(2)所示。

图13 自复位耗能支撑SAP2000模型示意Fig.13 Schematic diagrams of self-centering energy-dissipation braces in the SAP2000 model

(2a)

(2b)

Pa=P0+F

(2c)

加设自复位耗能支撑的摩擦力为4 kN,碟簧的预压力为4 kN,碟簧的刚度为0.2 kN/mm。SAP2000模拟得出的滞回曲线与理论曲线相近,因此可以采用简化自复位耗能支撑模拟,如图14所示。将简化模拟得到的自复位耗能支撑沿墙体对角线加设在剪力墙中,建立起加设支撑的冷弯型钢龙骨剪力墙。

4 结果分析和讨论

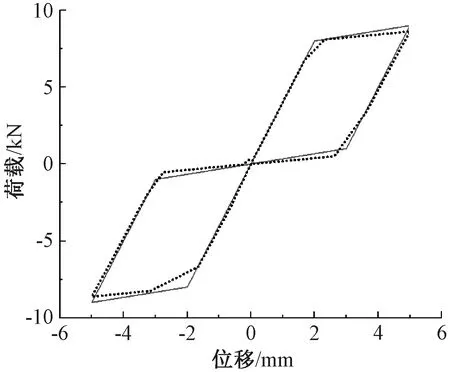
——理论滞回曲线; ……SAP2000模拟。图14 支撑滞回曲线Fig.14 Hysteretic curves of braces

4.1 有、无加设支撑的剪力墙对比

在变形方面,有、无支撑的冷弯剪力墙都会发生刚体转动,在面板接缝处会发生错缝现象。与试验现象[12]一致,如图15a和15c所示。

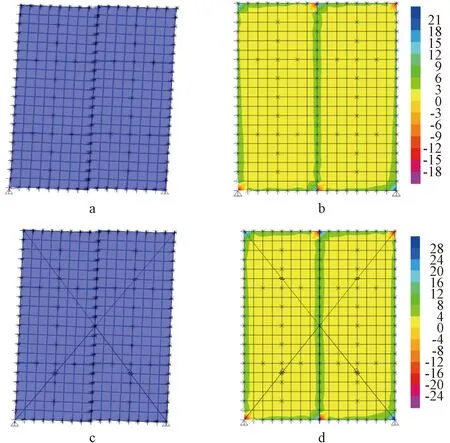
a—不加支撑的变形,mm; b—不加支撑的覆面板应力分布,MPa;c—加设支撑的变形,mm; d—加设支撑的覆面板应力分布,MPa。图15 变形及应力Fig.15 Deformation and stress

在应力方面,有、无支撑的冷弯剪力墙都会在面板四角处出现应力集中现象,此处应力值为最大,与试验现象一致。与边立柱连接处面板的应力值较大,面板中间区域的应力值最小。不加支撑的面板应力极值为21 MPa,加设支撑的极值为28 MPa,均出现在四角处;与边立柱连接处面板,不加设和加设支撑的应力分别为12,16 MPa;在面板内部,不加设和加设支撑的应力只有3,4 MPa。应力分布如图15b和15d所示。可以看出:加设支撑可以提高面板各部分所承受的应力,提高面板利用率,且破坏形式仍是连接处和四角处的破坏,并无破坏形式的变化。采用SAP2000模拟加设支撑的冷弯钢龙骨剪力墙与无支撑的剪力墙进行对比,可以发现:在承载力提高较小的情况下,加设支撑的摩擦力为4 kN时,能量耗散系数提高了18%。原因为:不加支撑的结构主要通过墙体本身耗能,加设支撑后的结构可以通过支撑和墙体耗能;其次,加设支撑后墙体面板的利用率得到提高,面板的耗能能力增强。加设支撑的墙体滞回曲线更加饱满,耗能面积更大,耗能面积提高了30%。在碟簧预压力为4 kN,碟簧刚度为0.2 kN/mm时,残余变形从72 mm下降到26.9 mm,下降到原来的37%左右,大大降低了残余变形。在加设支撑后结构的延性也有明显的增强,加设支撑可以提高结构的抗震性能。滞回曲线对比图和对比数据如图16和表4所示。

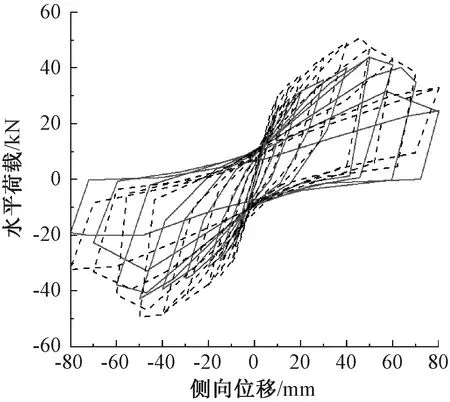
——不加支撑; ……加设支撑。图16 水平荷载与侧向位移的有无加设支撑对比Fig.16 Comparisons of horizontal loads and lateral displacement of walls with or without braces

表4 对比有、无加设支撑的数据Table 4 Comparisons of data of walls with and without additional braces

4.2 参数分析结果

为探究自复位耗能支撑各构件对钢龙骨剪力墙抗震性能的影响,将自复位构件按照施加的预应力和碟簧刚度进行分类,将耗能构件按照施加摩擦力进行分类。为了便于模拟结果展示,将各抗震性能参数参照标准化试件2(施加预压力4 kN,施加摩擦力4 kN,碟簧刚度0.2 kN/mm)进行归一化处理。

比较C-1～3与B-1可见:随着预压力的增大,峰值荷载小幅度的增加;延性有了较小的提升,因为屈服位移提前,极限位移后移使得延性变好;耗能系数下降不大;但是残余变形下降明显,从2 kN到8 kN,残余变形下降了50%。由此可知:改变预压力可以极大减小残余变形,对延性也有较小的提升,如图17所示。预压力的增大,可以提高剪力墙的恢复力,帮助结构复位。预压力的增大不影响结构的耗能面积,但是由于峰值荷载增大,能量耗散系数下降。

a—滞回曲线; b—预压力对抗震性能的影响。—峰值荷载; —延性; —耗能系数; —残余变形;——试件B-1; ……试件D-3。图17 试件B-1与C-1抗震性能对比Fig.17 Seismic property comparisons between specimen B-1 and C-1

比较D-1～3与B-1可见:随着摩擦力的增大,峰值荷载小幅度的增加;延性有了较小的提升,但是此时的延性变好是因为屈服位移和极限位移均提前,变化幅度较改变预压力更小;耗能系数小幅度提高,可能是因为施加的摩擦力相较于峰值荷载还是很小,所以耗能系数改善不明显;残余变形大幅度上升,从2 kN到8 kN,残余变形上涨接近1倍。由此可知:改变摩擦力可以使结构延性变好,但是残余变形明显增大,如图18所示。摩擦力的增加,可以显著提高结构的耗能面积,但是由于峰值荷载也增加,所以耗能系数没有明显的改善,当摩擦力大于碟簧预压力,支撑不能完全自复位,整体剪力墙结构的残余变形就会显著增加。

a—滞回曲线; b—预压力对抗震性能的影响。——试件B-1; ……试件D-3。—峰值荷载; —延性; —耗能系数; —残余变形。图18 试件B-1与D-3抗震性能对比Fig.18 Seismic property comparisons between specimen B-1 and D-1

比较E-1～3与B-1可见:随着碟簧刚度的增大,峰值荷载在小幅度的增加;延性变差,此时的延性屈服位移和极限位移均后移;耗能系数小幅度下降,但比改变摩擦力和预压力时耗能系数变化明显;残余变形大幅度下降,从0.1 kN/mm到0.4 kN/mm,残余变形下降了不到40%。由此可知,改变碟簧刚度可以使残余变形减小,但是同时结构延性变差。如图19所示。碟簧刚度和支撑的恢复力成正比,能减小结构残余变形。但碟簧刚度不影响结构的耗能面积,但是碟簧刚度的增加,结构的峰值荷载也相应增加,能量耗散系数小幅度下降。