蝶形耗能连接件装配式梁柱节点的抗震性能*

李 慧 许 浒 欧 盈 余志祥 赵城熠 高文君

(1.西南交通大学土木工程学院,成都 610036; 2.中铁第一勘察设计集团有限公司,西安 710043)

装配式结构是当前建筑业的一大发展趋势,而梁柱连接节点是其中的关键之处,直接决定了装配式结构的整体抗震性能。[1-3]在装配式混凝土结构中,梁柱节点连接形式可分为干式和湿式两种,其中,干式连接不需要在施工现场进行混凝土浇筑,绿色环保,省工省时,在发展前景上更具优势。然而,目前既有的干式连接节点构造较为复杂,对施工精度要求较高,节点连接技术不够成熟,对该类节点开展的研究不够系统和全面,从而造成了干式连接节点发展的滞缓,使其得不到广泛的推广与应用。[4-6]国内外学者分别研究了许多不同连接形式干式节点的受力性能,结果表明节点力学性能会因不同构造形式而产生明显差异,对干式连接处各构件参数的合理设计是优化节点力学性能的关键。[7-13]由此可见,节点的构造形式、细部构件的选择和参数优化设计是干式连接中亟待进一步研究的方向。

鉴于此,提出了一种基于螺栓连接的蝶形耗能连接件装配式梁柱节点,该新型干式连接节点具有构造简单、便于施工等特点。研究采用ABAQUS程序对节点进行有限元分析。首先,结合现浇钢筋混凝土梁柱节点和螺栓连接钢结构梁柱节点的试验结果,对节点模型有限元计算方法的有效性进行验证,在此基础上,研究该新型干式连接节点的抗震性能,并对相关设计和构造参数展开了进一步的分析和优化。最后,利用有限元分析软件MIDAS,参照某实际工程,建立了采用优化后新型节点构建而成的整体框架结构模型,通过动力弹塑性时程计算,对比分析现浇结构与采用新型干式连接节点的装配式结构的地震响应,评估该优化后新型干式连接节点对结构整体抗震性能的影响。

1 蝶形耗能连接件装配式梁柱节点

蝶形耗能连接件装配式梁柱节点构造如图1a所示,采用在连接部位设置塑性铰的形式,将连接位置设置于梁柱节点核心区外一段距离的梁内,该距离一般可取梁截面有效高度的1倍,以保证节点核心区的完整性。该新型连接节点主要由蝶型耗能连接件、U型端板、拼接钢板、销轴和高强螺栓等部分组成,[14]连接形式如图1b所示。其中,两块U形端板采用Q345级钢材,分别预埋于预制混凝土梁端和柱端,通过销轴进行铰接,销轴使用材料为35CrMo合金钢材。U型端板上、下两侧通过材料为Q345级钢材的长螺孔型拼接钢板连接,并采用10.9级M20承压型高强螺栓进行固定。蝶型耗能连接件则设置在节点左、右两侧,由预埋在混凝土中的普通螺栓连接,耗能连接件与普通螺栓均采用Q235级钢材。

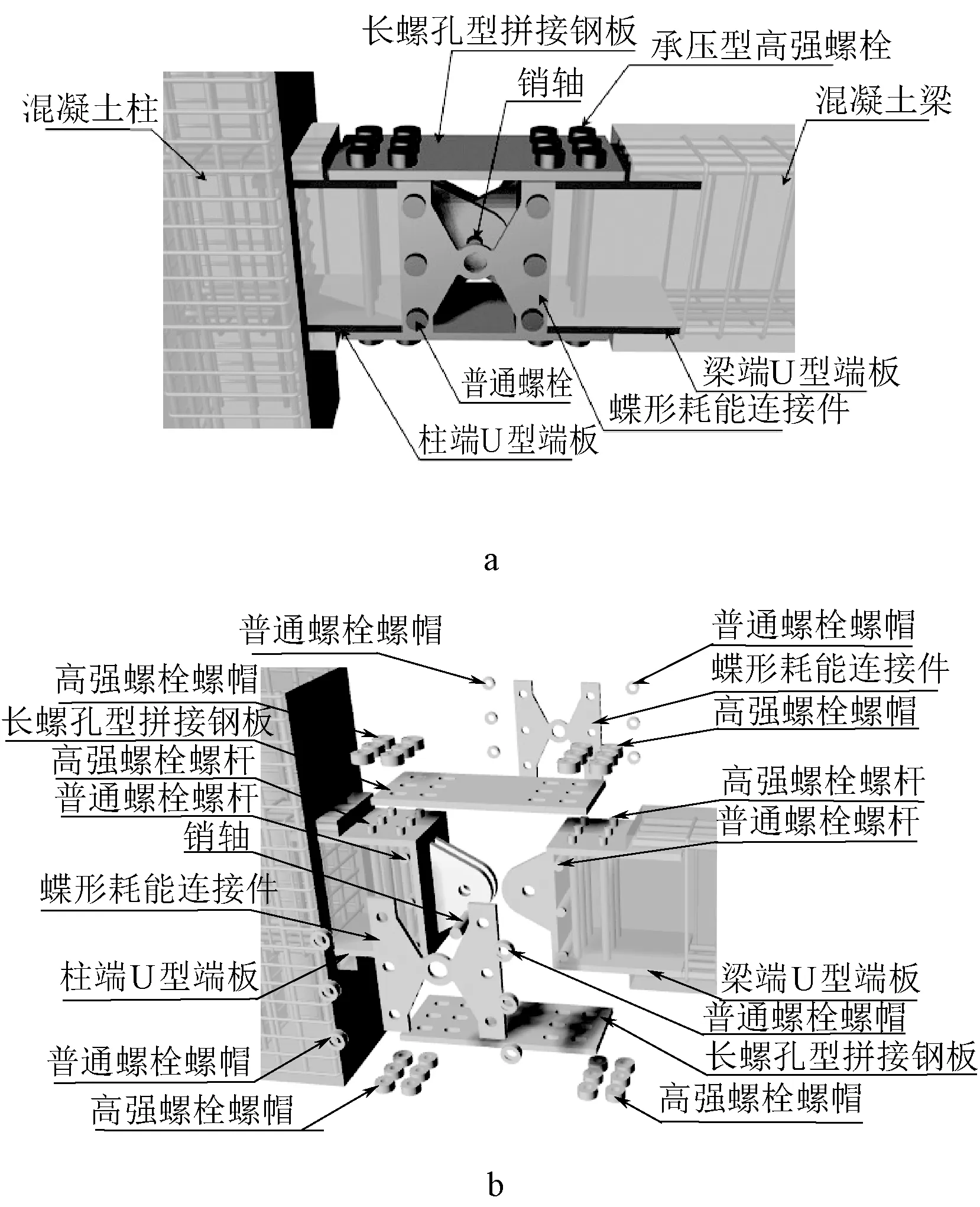
a—构造示意; b—连接示意。图1 蝶形耗能连接件装配式梁柱节点Fig.1 Prefabricated beam-column joint with butterfly-shaped energy consumpution connectors

节点整体设计具有明确的传力路径,即节点中部铰节点主要承担并传递剪力,上下两侧拼接钢板主要承担并传递弯矩。蝶形耗能连接件受力机理如图2所示,该构件可通过中部圆孔塑性变形耗散地震能量,[15]长螺孔型拼接钢板可使节点通过摩擦滑移耗散部分能量,与蝶形耗能连接件互相协同,从而增强节点的延性与耗能能力。同时,拼接钢板长螺孔的设计还可给高强螺栓的安装提供一定的空间,在一定程度上解决了节点施工安装时易产生的误差问题。

图2 蝶形耗能连接件机理Fig.2 Mechanisms of butterfly-shaped energy consumpution connectors

2 节点数值模型验证

基于三维精细有限元模型的数值计算是研究节点力学性能的主要技术手段之一。[16-18]为保证数值计算结果的可靠性,须先对模型涉及的单元类型、本构模型、边界条件以及其他相关参数等进行验证。结合提出的新型节点的特征,依托文献[19]中的现浇钢筋混凝土梁柱节点模型试验(MCB)和文献[20]中的螺栓连接钢结构梁柱节点模型试验(QZ1),采用ABAQUS程序对该两组试验节点开展相应的数值模拟,通过与试验结果分别进行对比分析,对节点有限元模型中的关键参数设置进行验证。

2.1 现浇混凝土梁柱节点模型

现浇梁柱节点试验模型(MCB)中混凝土强度等级为C55,梁构件尺寸为200 mm×380 mm×1 420 mm,柱构件尺寸为300 mm×300 mm×980 mm,具体构造及配筋详见文献[19]。模型加载方式如图3a所示,采用1 000 kN千斤顶作用于柱端,由此施加竖向轴压力,轴压比控制为0.4,加载采用 500 kN推拉千斤顶作用于节点试件梁端,由此施加低周往复荷载。整个加载阶段可划分为弹性、弹塑性两个阶段,弹性阶段采用荷载分级加载,弹塑性阶段采用位移控制加载,当加载至大位移情况下横向荷载不再增加或略有下降时,试验结束。

通过ABAQUS程序建立与MCB试件一致的现浇混凝土节点三维精细有限元模型,如图3b所示,有限元模型尺寸与试验一致,对框架柱底面结点约束三向自由度,顶面节点释放竖向约束,同时设置刚性垫片于梁端位置,用于给结点模型施加低周往复荷载。混凝土采用8结点六面体线性非协调模式单元,网格尺度为40 mm,共计3 622个六面体实体单元,材料本构采用塑性损伤模型[21-22],应力-应变关系的选择参照文献[23-24],取拉伸恢复因子为0,压缩恢复因子为0.6。钢筋采用线性剪切变形梁单元,应力-应变关系[25]如图4所示,钢筋与混凝土单元之间采用同位结点耦合方式进行约束。

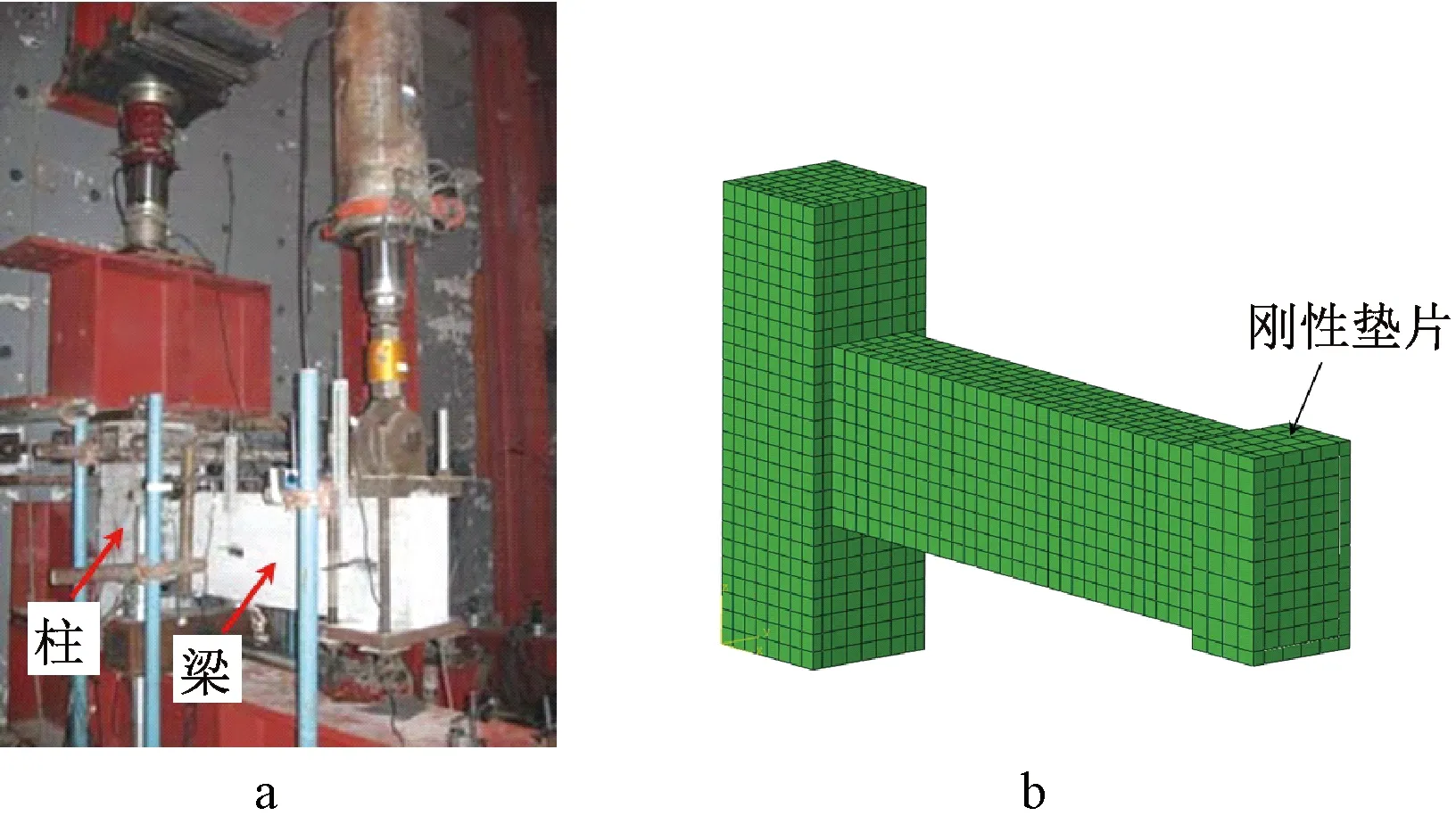
a—试验模型[19]; b—有限元模型。图3 现浇钢筋混凝土梁柱节点模型Fig.3 Models of cast-in-place reinforced concrete beam-column joints

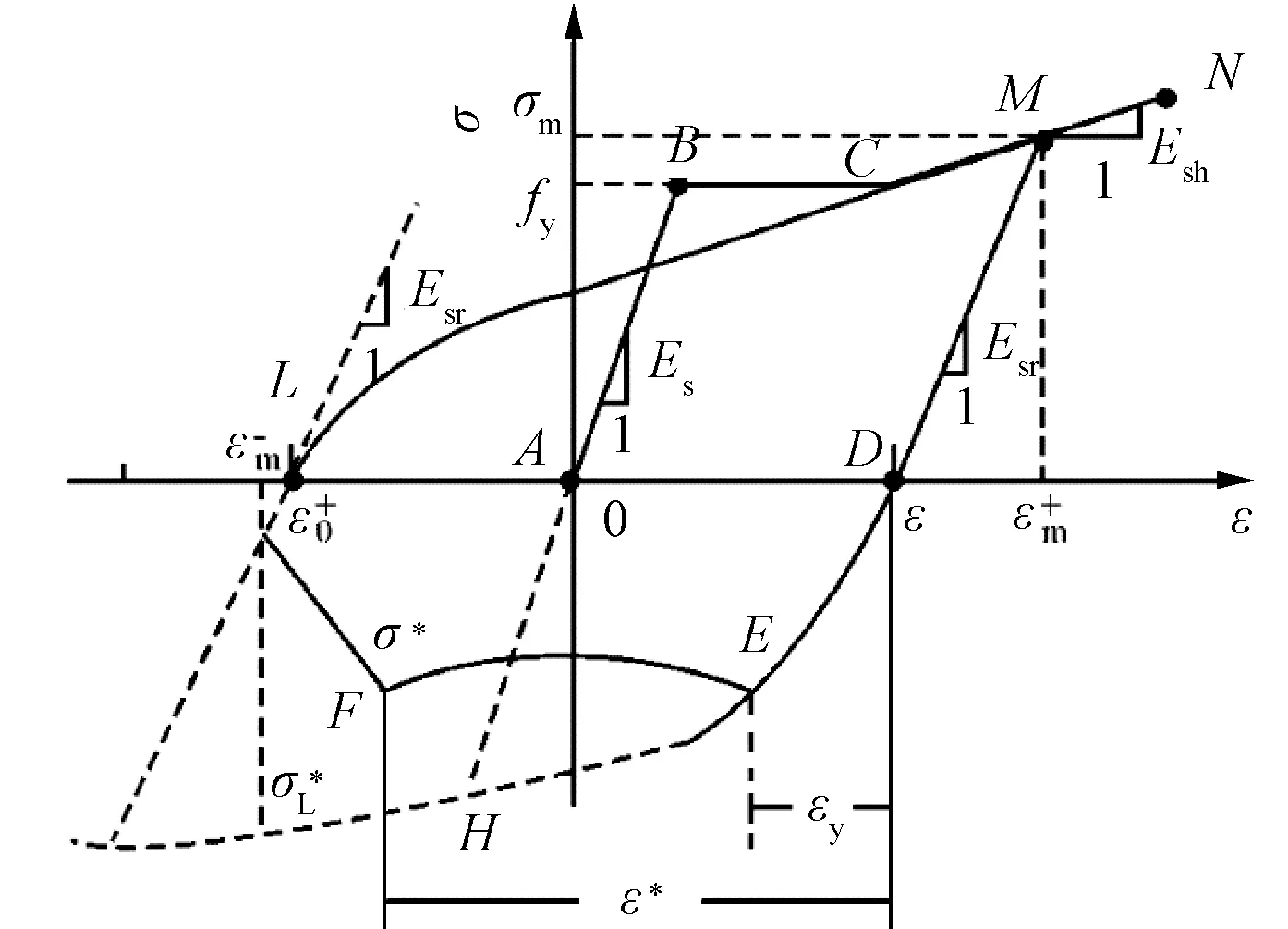
图4 钢筋应力-应变曲线[25]Fig.4 Stress-strain curves of rebars

2.2 螺栓连接钢结构梁柱节点模型

螺栓连接钢结构梁柱节点模型(QZ1)中,梁构件长度为1 550 mm,截面尺寸为HM350×175×7×11,柱构件高度为3 300 mm,截面尺寸为HW350×350×12×19,梁柱均采用Q235B热轧型钢,梁柱节点处腹板连接与翼缘连接均采用10.9级高强螺栓,直径分别为22,24 mm。试验加载形式如图5a所示,采用平位布置,即将柱横放且柱两端采取固定约束,梁竖直放置。利用推拉千斤顶作用于梁端,对构件进行低周往复加载,加载分两阶段进行,屈服之前采用荷载分级加载至120 kN,屈服之后改用位移加载,加载至承载力下降到峰值荷载的85%以下时,试验终止。

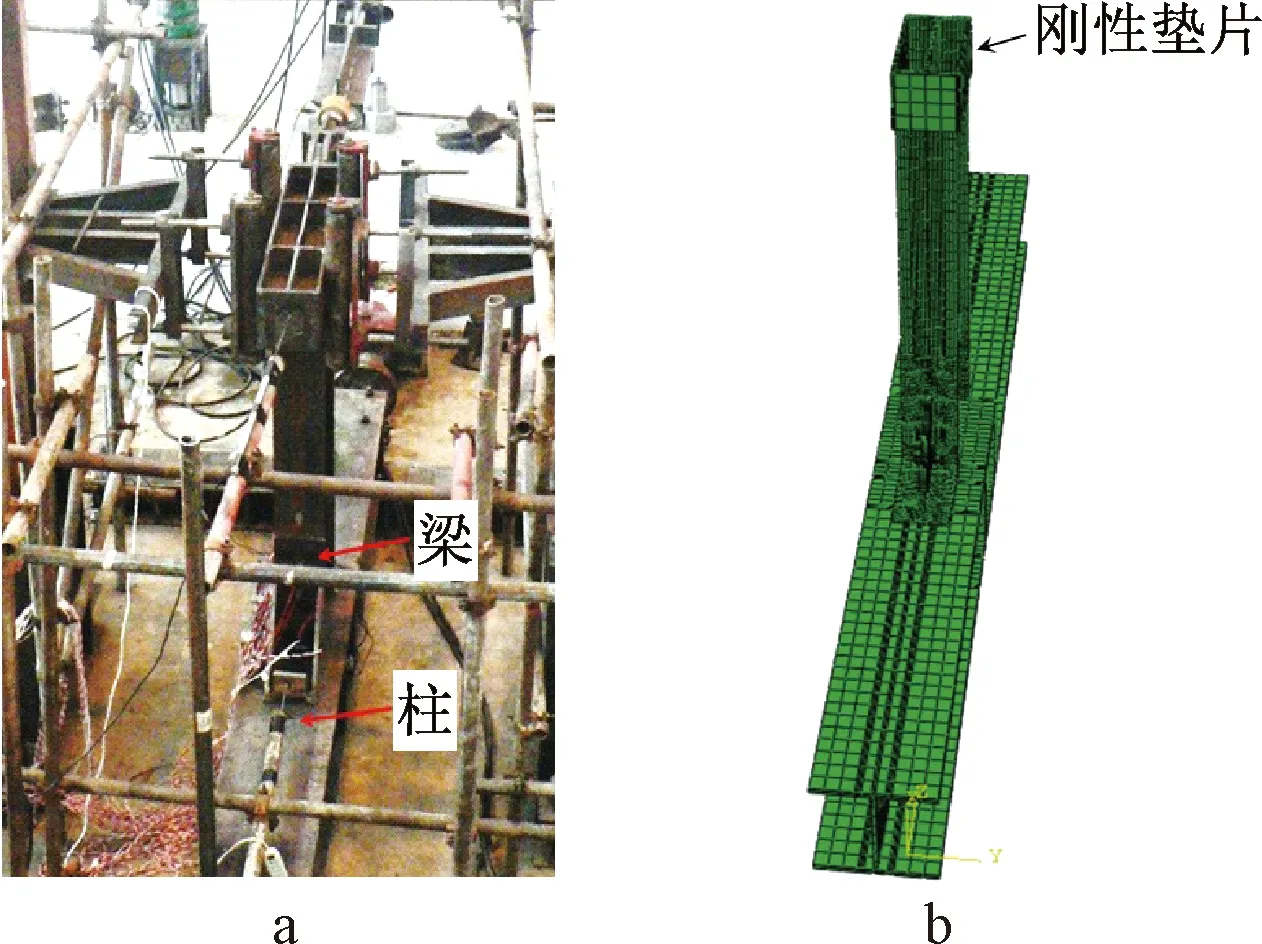
a—试验模型[20]; b—有限元模型。图5 螺栓连接钢结构节点模型Fig.5 Models of steel structure joints connected by bolts

通过ABAQUS程序建立与QZ1试件一致的螺栓连接钢结构梁柱节点有限元模型,如图5b所示。其中,螺栓和型钢均采用8结点六面体线性非协调模式单元,网格尺度在梁柱连接处进行加密处理,计算模型共计65 257个六面体实体单元。钢材本构关系均采用双线性随动强化模型,选用Mises屈服准则,考虑0.01E(E为钢材弹性模量)的应力强化。将钢材线膨胀系数设为1.2×10-5,通过对高强螺栓单元设置温差作用实现预紧力的施加,大小为155 kN。焊接部位的节点采用约束方程实现自由度耦合,相互接触的部件采用通用接触算法设置接触对。模型的加载制度与试验保持一致,均通过梁端的刚性垫片传递荷载。

2.3 对比验证

滞回曲线体现了结构的综合抗震性能,将有限元滞回曲线与试验进行对比可以用于验证有限元模型和计算参数的有效性。MCB模型与QZ1模型的试验结果与有限元计算结果的对比如图6所示,相关特征值列于表1。

a—MCB模型;b—QZ1模型。——试验; 有限元。图6 有限元分析法和试验的滞回曲线Fig.6 Hysteretic curves by finite element analysis and tests

表1 节点特征值Table 1 Eigenvalues of joints

由图6、表1可知:MCB模型的有限元与试验的屈服位移及屈服荷载相近,峰值荷载出现位置和大小基本一致;由于在有限元模型中选用的本构关系,考虑了钢筋屈曲影响,没有考虑钢筋与混凝土间的黏结滑移因素,故数值模拟得出的滞回曲线在形状上比试验曲线饱满,两者总滞回耗能具有36.9%的偏差。但从总的来看,MCB模型的有限元计算所得滞回曲线与试验滞回曲线基本吻合。QZ1模型有限元与试验的屈服位移及屈服荷载相近,同时,由于选用的钢材本构模型中定义了屈服后的强化段,因此未发生试验中出现的翼缘、腹板翘曲的现象,有限元模型计算所得滞回曲线中峰值荷载也未出现下降,峰值位移与试验结果相差较大。在滞回曲线的形状上,QZ1模型的有限元计算与试验所得曲线均较为饱满,由于螺栓受力后发生了滑移,曲线在整体形态上产生了一定程度的“捏缩效应”。在总滞回耗能上,QZ1模型的有限元与试验结果具有11.3%的偏差,但总的来看,两者滞回曲线包络面积相差不大,吻合度较好。综上可以看出,上述选用材料本构模型及有限元计算方法是有效及可行的。

3 蝶形耗能连接件装配式梁柱节点有限元分析

基于上述数值计算方法,对提出的新型干式连接节点开展拟静力分析,获得该新型干式连接节点在低周往复荷载作用下的滞回曲线以及一些相关关键指标(刚度退化、等效黏滞阻尼比、延性系数等)的变化规律,并对照现浇节点的模型计算结果,分析该新型节点抗震性能。

3.1 新型节点模型建立

按照文献[19]中现浇节点尺寸及边界条件建立有限元模型(图7),柱端轴压比按0.4考虑,梁端设有刚性垫片,用于施加位移荷载。混凝土和钢材材料模型以及各部件之间的连接约束关系均按照前文方法进行设置。混凝土构件单元的平均网格尺度为50 mm,为了重点考察钢结构连接件的应力、应变响应,该部分的网格尺度适当加密,按5 mm建模。混凝土梁端的U型端板钢构件与混凝土单元间采用绑定接触,耦合其自由度。构件钢材间的摩擦系数均取为0.2,对节点连接处竖向螺栓施加预紧力为155 kN。采用隐式静力算法计算求解,同时考虑力、位移收敛准则,收敛容差分别为0.005、0.01。

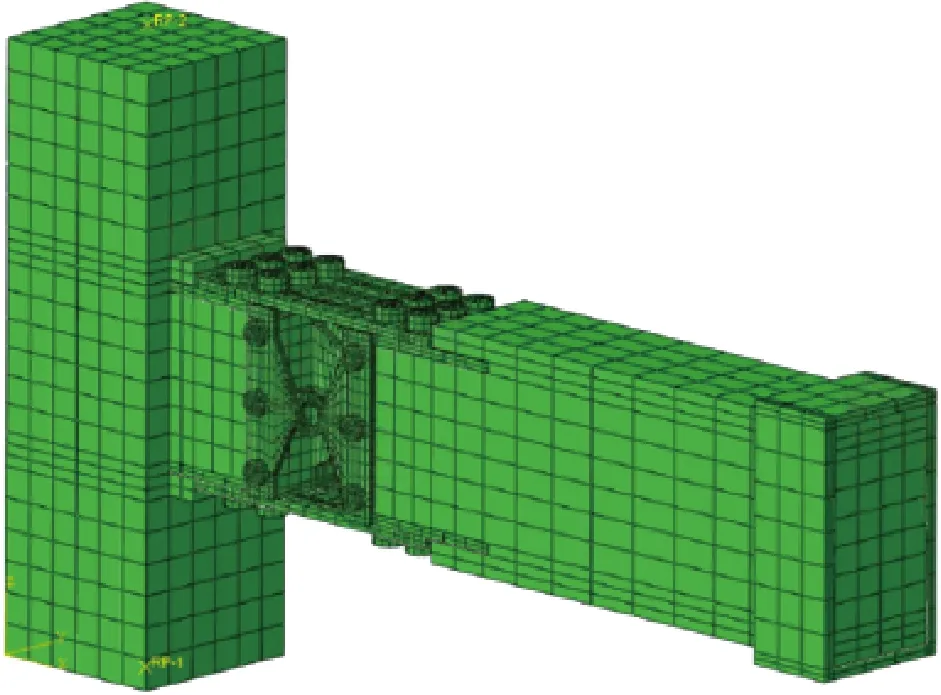
图7 新型节点有限元模型Fig.7 A finite element model of the new joint

3.2 计算结果

图8给出了新型节点的加载全过程滞回曲线。可知:该滞回曲线形状整体较为饱满,新型节点具有良好的变形能力与耗能能力;在加载初期,新型节点处于弹性阶段,荷载与位移呈线性关系;位移加载至8 mm时,滞回曲线开始出现水平段,节点螺栓开始滑移,滞回环面积逐渐增大,力与位移逐渐呈非线性关系;新型节点的峰值位移为30 mm,此时节点承载力最大,加载至30 mm后,滞回曲线开始下降,新型节点进入破坏阶段。

——新型节点; 现浇节点。图8 新型节点和现浇节点的滞回曲线Fig.8 Hysteretic curves of the new joint and the cast-in-place joint

由图8中新型节点与现浇节点计算所得滞回曲线的对比可知:新型节点与现浇节点在加载初期的曲线增长速率基本一致;随着位移荷载的增加,新型节点和现浇节点滞回曲线对角线的斜率逐渐减小;新型节点与现浇节点的极限承载力相当,其中,新型节点的荷载峰值点位置出现较早;由于新型节点钢构件连接处螺栓发生滑移,相比于现浇节点,新型节点滞回曲线的包络面积略大,表现出较强的耗能性能。

3.3 关键指标

主要依据新型节点延性系数、等效黏滞阻尼比、滞回耗能和刚度退化等重要指标,并与现浇节点进行对照,用于衡量新型节点试件的抗震性能。相关指标列于表2和图9。可知:新型节点的阻尼系数在加载前期迅速增长,加载至30 mm后,略有下降;随着新型节点加载位移的增加,节点相应的滞回耗能也逐渐增长,且在加载初期增长较快;新型节点在整个加载过程中体现出了较为明显的刚度退化,加载前期节点刚度下降较为显著,后期则逐渐趋于平缓。

表2 节点位移和延性系数Table 2 Displacement,ductility coefficients of joints

a—等效黏滞阻尼比-位移曲线; b—滞回耗能-位移曲线; c—刚度退化曲线。 新型节点; 现浇节点。图9 关键指标对比Fig.9 Comparisons of key indicators

通过新型节点与现浇节点的各项指标对比可知:新型节点屈服位移略大,峰值位移是现浇节点的1/2,计算得出的延性系数约为现浇节点的1/3,在位移延性方面,新型节点表现较弱;在加载初期,可见新型节点阻尼比、滞回耗能及等效刚度均大于现浇节点,这是由于新型节点采用了螺栓连接以及使用了耗能连接件,因而体现出的耗能能力较强;新型节点的阻尼比在加载至30 mm时开始呈现下降趋势,至60 mm时开始低于现浇节点;新型节点的滞回耗能在加载至50 mm后,开始小于现浇节点,但在加载全过程中总的滞回耗能上,新型节点略大于现浇节点;新型节点与现浇节点的等效刚度随着加载位移的增加,逐渐退化至一致。

4 新型节点参数分析及优化

4.1 参数设计

为了明确新型节点抗震性能影响因素,分别以高强螺栓预紧力大小、拼接钢板接触面摩擦系数大小和蝶形耗能连接件及其圆孔孔径大小作为参数变量,另设计了11组不同计算模型,开展单参数分析,通过计算对比进一步对新型连接节点的构造和设计参数进行优化。各模型编号及参数设置如表3所示,其中,X0为前文中的基本模型,基于此模型,增设以预紧力为变量的模型A1～A4,以拼接钢板接触面摩擦系数为变量的模型B1～B3,以圆孔孔径尺寸为变量的模型C1～C4,C4表示无蝶形耗能连接件模型。

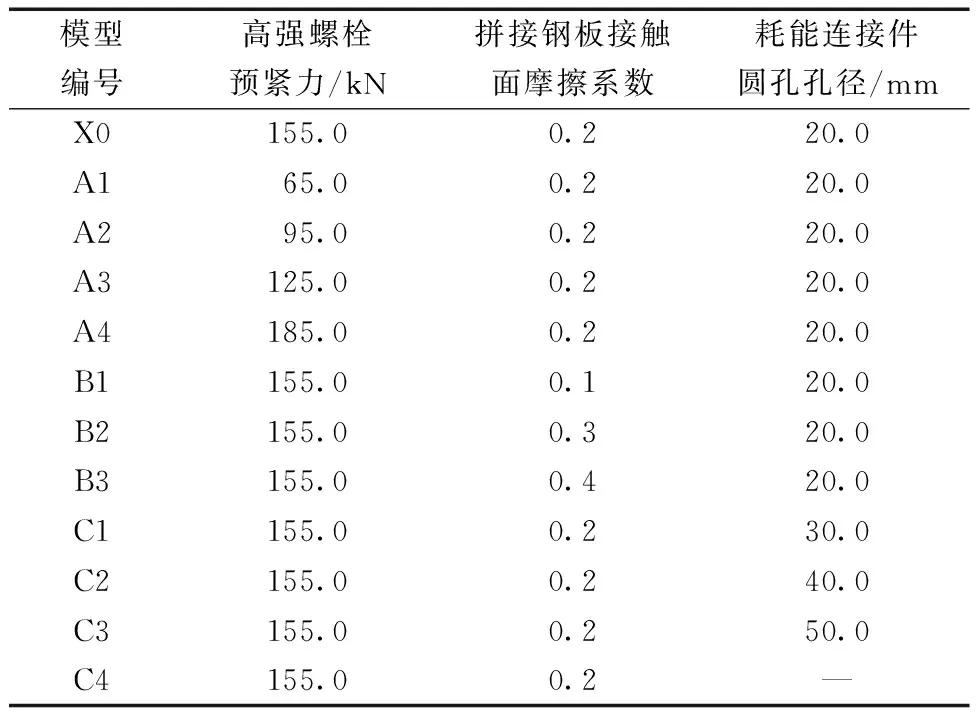
表3 模型编号及节点参数Table 3 Model numbers and joint parameters

4.2 参数分析

对12个节点模型计算所得相关数据均相应列于表4中。

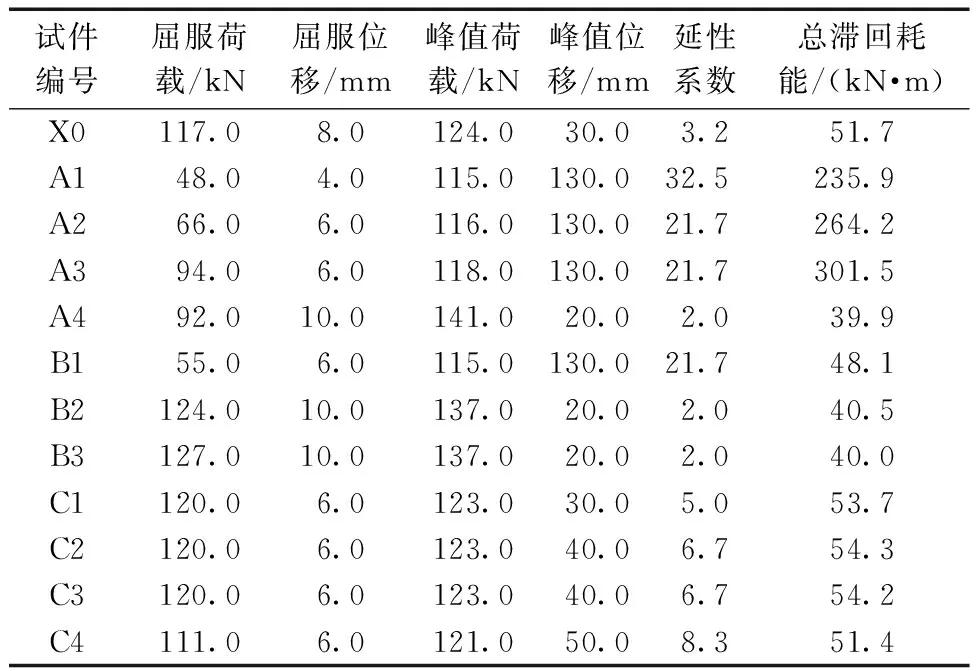
表4 节点参数对节点力学性能的影响Table 4 Influence of joint parameters on mechanical properties of joints

根据表4中X0与A1～A4模型的对比可看出:高强螺栓预紧力对节点的力学性能存在显著影响,施加的预紧力越大,节点的峰值荷载越大,但预紧力超过125 kN后,节点峰值位移显著减小,延性较差;预紧力为125 kN时节点的总滞回耗能最高,超过125 kN后,螺栓的滑移受到限制,节点的耗能性能降低。

根据X0与C1～C4模型分析可知:无耗能连接件的C4模型,其屈服荷载和峰值荷载最低,延性系数最高,说明该蝶形耗能连接件的应用可以提升节点承载力,但会降低节点延性;有蝶形耗能连接件的新型节点模型,在连接件圆孔孔径尺寸不同时,节点的屈服荷载和峰值荷载基本一致,峰值位移也比较接近,孔径尺寸不超过40 mm时,节点滞回耗能随孔径增大而增加,超过40 mm后有所降低,但从整体数值上比较,该组模型中总滞回耗能的最大相差值未超过3 kN·m,说明耗能连接件圆孔孔径尺寸的大小不会对新型节点的耗能性能产生较大影响。但根据有限元模拟结果显示,耗能连接件圆孔尺寸会影响模型耗能能力的发挥,耗能连接件圆孔尺寸越大,其耗能能力发挥得越充分,其中孔径尺寸为50 mm的C3模型耗能能力发挥得最为充分。

5 新型节点装配式框架整体分析

5.1 恢复力模型

采用蝶形耗能连接件装配式梁柱节点,开展典型多层框架整体结构分析。首先,基于前文优化对比结果,选取高强螺栓预紧力125 kN,拼接钢板接触面摩擦系数0.2,圆孔孔径50 mm作为节点定型设计参数。通过滞回分析确定蝶形耗能连接件装配式梁柱节点骨架曲线,并基于拟合法,依次连接节点的屈服点、峰值点和破坏点得到其三折线恢复力模型,如图10中CBAA′B′C′所示。由图10可见:新型节点处于弹性阶段时,即位移达到A点前,卸载刚度与弹性阶段的初始刚度K0基本一致,保持为A′OA直线段;位移达到A点后新型节点进入屈服阶段,强度出现明显退化,滞回发展路径为1—2—3—4,当加载至峰值点B后,节点强度、刚度发生严重退化,滞回曲线发展路径为a—b—c—d。

图10 恢复力模型Fig.10 A resilience model

节点在往复荷载作用下,不同加载阶段的刚度表示如式(1)～(4)所示:

正向卸载刚度退化规律K1:

(1)

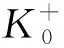
负向加载刚度退化规律K2:

(2)

式中:Δu+为正向加载峰值荷载时的位移。

负向卸载刚度退化规律K3:

(3)

正向加载刚度退化规律K4:

(4)

式中:Δu-为负向加载峰值荷载时的位移。

5.2 结构整体模型

设计了一个4层框架结构,该结构参考某工程实例,结构为矩形平面,纵向共5跨,每跨长为3.6 m;横向共3跨,跨度分别为3.6,1.8,3.6 m;建筑层高3.2 m,设计地震分组为第一组,场地类别II类,场地特征周期Tg=0.35 s,抗震设防烈度为8度(0.2g),抗震设防类别为乙类,抗震等级为一级。梁柱构件纵筋与箍筋分别采用HRB335和HPB235,混凝土材料强度等级为C55。

运用工程设计软件MIDAS建立一个采用优化后新型节点构建而成的结构体系整体模型(Z1)和一个同尺寸现浇结构体系整体模型(Z2),并对Z1、Z2两组模型开展罕遇地震下的动力弹塑性时程分析。其中,框架柱和框架梁均选用实腹式矩形截面,截面尺寸分别为300 mm×300 mm和200 mm×380 mm。建立框架模型时,梁、柱构件单元类型均选用梁单元。边界选用一般支承嵌固底层柱底各节点,设置梁单元连续荷载为7 kN/m,楼面恒荷载为5 kN/m2,楼面活荷载为2 kN/m2,模型考虑结构单元所受的重力,并于质量控制参数中考虑将结构单元所受的重力转换为质量,转换方向选择X、Y、Z地震作用方向,计算分析类型选择子空间迭代法,振型数量为6。对于蝶形耗能连接件装配式梁柱节点在Z1模型中采用等效处理,即将节点塑性铰设置在梁端,并忽略节点区至柱端的距离,通过赋予其恢复力模型模拟节点在地震动力作用下的力学响应。在MIDAS软件材料特性设置中,定义框架塑性铰特性值时,各参数设置如表5所示。为开展非线性动力时程分析,按照GB 50011—2010《建筑抗震设计规范》[26]要求选取3条地震波,其名称及相关参数如表6所示。

表5 框架塑性铰特性值定义Table 5 Definition of eigenvalues of plastic hinges of frames

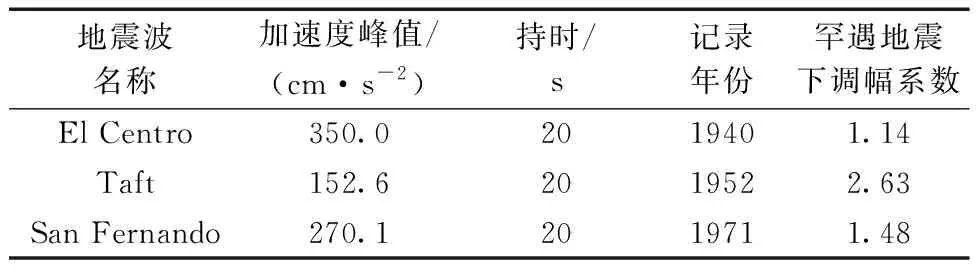
表6 地震波参数Table 6 Parameters of earthquake waves

Z1模型与Z2模型在修正El Centro波作用下的塑性铰分布如图11所示。其中Level 1～Level 5分别对应构件未屈服、立即使用、安全、全截面屈服和破坏。可知:在塑性铰分布情况上,Z1模型与Z2模型较为相似,但相比于Z1模型,Z2模型存在较多构件塑性铰已经进入全截面屈服状态。

a—Z1塑性铰分布;b—Z2塑性铰分布。水平5; 水平4; 水平3; 水平2; 水平1。图11 Z1、Z2塑性铰分布Fig.11 Distribution of plastic hinges of Z1 and Z2

Z1模型与Z2模型的层间位移角如图12所示,两组模型的曲线变化趋势基本一致,Z1模型在地震作用下结构响应略大,但均符合GB 50011—2010的要求,即最大层间位移角均未超过1/50。

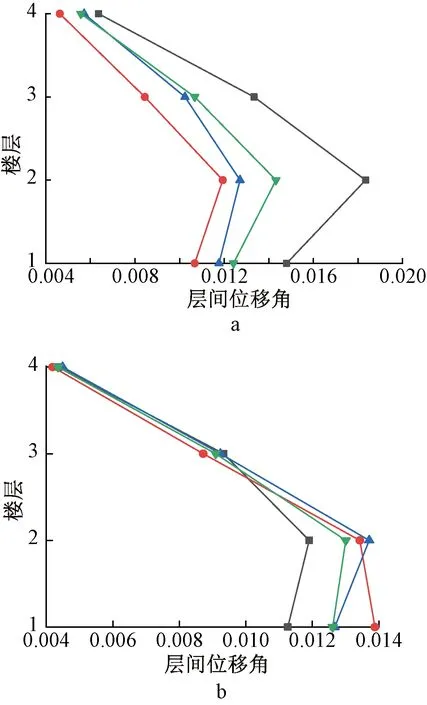
a—Z1; b—Z2。Taft; El Contro; San Fernando; 平均值。图12 Z1、Z2层间位移角Fig.12 Inter-story drifts of Z1 and Z2

图13为Z1与Z2两组模型分别在表5所列3条地震波作用下X方向的顶点时程位移曲线。可见:两组模型顶点位移峰值较为接近,但在每个波峰的出现时间上看,均表现为Z1稍晚于Z2,分析其原因是由于该新型节点中存在的摩擦滑移特性发挥了作用。综合来看,两组模型顶点时程位移曲线变化趋势相似。

a—Taft波;b—El Centro波;c—San Fernando波。——Z1; Z2。图13 顶点时程位移曲线Fig.13 Time-history curves of displacement of the top

6 结束语

采用ABAQUS软件建立了蝶形耗能连接件装配式梁柱节点的有限元模型,并通过与现浇模型对比,完成了对该新型干式连接节点抗震性能的分析,并对其展开了参数分析,得到了优化后节点的恢复力模型,在此基础上,通过MIDAS软件建立了采用该优化后新型节点构建而成的结构体系整体模型并完成了对该模型的动力弹塑性时程分析,得出结论如下:

1)蝶形耗能连接件装配式梁柱节点的滞回曲线形态饱满,具有较好的耗能性能,能满足结构抗震需求。

2)高强螺栓预紧力及拼接钢板接触面摩擦系数均会对蝶形耗能连接件装配式梁柱节点的抗震性能造成较为显著的影响。以预紧力为分析变量时,其值为125 kN时新型节点表现出的耗能性能最好;以摩擦系数为分析变量时,新型节点在摩擦系数为0.2时表现出的耗能性能最好。新型节点的延性与耗能能力会因预紧力或摩擦系数设置过大而明显降低。

3)蝶形耗能连接件装配式梁柱节点中,蝶形耗能连接件利于提升节点承载能力,同时也会降低节点延性。耗能连接件的孔径尺寸对节点承载能力及耗能性能的影响不大,但尺寸越大,耗能连接件的耗能能力发挥得越充分。

4)经参数优化改进后的节点结构框架体系表现出的抗震性能与现浇框架结构基本相当,蝶形耗能连接件装配式梁柱节点在装配式混凝土结构的实际应用中具有一定的可行性。