PCA-GA-BP 算法在爆破振动预测中的应用

2023-05-23牛本亮

中国建筑金属结构 2023年4期

牛本亮

（中铁十六局集团有限公司，广东深圳 518000）

0 引言

随着城市的发展，城市地下工程施工越来越多，爆破作业是地下工程施工中最常见的岩石开挖方法之一。基坑距离建筑较近时爆破振动会对周围建筑产生不利影响，如果不能准确控制这个问题，就会导致对相邻结构的损害。近年来许多研究都致力于爆破振动的准确预测，Rajabi[1-2]等人使用人工神经网络对多组实测数据进行训练得到适用于引起地面振动的预测模型。Arthur[2]等对13 种BPNN 训练算法作出分析对比，评估了用于构建B-NN 模型各种训练算法的性能，得到了最适宜于训练算法是BFGS 拟牛顿算法。Nguyen[3-7]PSO 等则基于深度神经网使用多种算法对神经网络进行优化，并认为爆破的装药量、监测距离以及时间延迟是预测地面振速的必须参数。苟倩倩[8，9]等利用PCA 对11 个影响爆破振动的参数进行主成分分析，该法优化了后神经网络的输入层特征，有效的减少了模型误差，但由于模型初始生成的权值和阈值对于在一定程度上则影响了预测精度。

上述研究者将人工神经网络应用于爆破振动预测分析已有一定的工程经验，并取得不错的效果，但研究者对神经网络参数优化时并未对输入层、权值以及阈值同时进行优化，对此本文使用主成分分析法和遗传算法同时使用对BP 神经网络进行优化，形成一种具有较好预测精度的PCA-GA-BP 预测模型，研究结果可对爆破振动控制和预测起到一定的参考作用。

1 PCA-GA-BP

1.1 PCA

影响爆破振动的因素是众多的，但如果都把这些因素考虑到实际计算中，无疑会增加分析问题的复杂性，使问题的解决变得愈发困难，为了简化分析问题的难度，采用主成分分析法可以做到将影响问题的多个特征转换为主要的几个，抽取出较为有效的变量，该方法的主要计算步骤如下：

（1）原始数据标准化；

（2）计算协方差矩阵的特征值和特征向量；（3）计算贡献率和累积贡献率；（4）提取主成分。

1.2 GA-BP

遗传算法的主要思想是模仿生物界的“适者生存”的进化规则，该算法具有全局搜索和优化的能力，利用其优化BP 的主要过程为：随机生成神经网络的权值和阈值，即个体长度，并进行编码操作，最后通过适应度函数确定选出满足精度的最优个体。

2 案例分析

2.1 工程背景

深圳市16 号线管廊综合井5 的爆破工程量约4 800m³，爆破主区域位于黄阁路与龙平西路交叉口东南侧，竖井南侧16.4m 为新大新家具广场，四层条形基础楼房，周边整体环境如图1 所示。

图1 爆破场地示意图

由于本项目所在场地尚未进行爆破施工，本文选取文献[6]中的40 组监测数据来检验文中所提方法的可行性，并将该方法应用于此工程后续的爆破振动监测预测中，从而达到有效控制爆破振动对周边建（构）筑物的不利影响。选取孔深（m）x1、超深（m）x2、填塞（m）x3、底盘抵抗线（m）x4、孔距（m）x5、排距（m）x6、最大段药量（kg）x7、炸药单耗kg·m-3x8、高程差（m）x9以及爆心距（m）x10作为影响爆破振速（cm·s-1）y的主要因素。

2.2 主成分提取

按照主成分分析的步骤，使用引文中的40 组数据，利用matlab 软件计算得到各成分之间的贡献率和累积贡献率如表1 所示。

表1 特征值、贡献率及累积贡献率

由表1 可知前5 个因子的累积贡献率达到了85.4%，这表明这5 个主成分包含着原始数据的大部分信息，可作为主成分抽取，模型的特征数由原来的10 维降为5 维，这将利于模型计算速度的提升和收敛。根据计算得到的因子荷载矩阵计算得到主成分表达式为：

式中：各字母代表的含义。

2.3 模型参数设置及评估指标

（1）BP 神经网络参数确定

将提取到的5 个主成分作为神经网络的输入层，隐含层根据经验式（2）确定为6 时训练效果较好，输出层参数为爆破振动速度[7]。

式中，n为隐含层个数，xi，yi分别为输入层节点数和输出层节点数，α在0 到10 之间取值。根据主成分计算的得分得到新的数据集，并将其按照4:1 的比例来划分测试集和训练集，即训练集32 个样本，测试集8 个样本。神经网络的训练次数为1 000，训练目标为0.0001，学习速率为0.1，动量因子为0.01，至此网络的拓扑结构确定为5-6-1；为了对比分析，设置标准BP 神经网络的拓扑结构为10-12-1，PCA-BP 的网络拓扑结构为5-6-1；其余参数设置均相同。

（2）遗传算法参数确定

采用二进制编码确定个体的编码长度，其中权值和阈值的个数为47，从而确定个体的编码长度为47，初始种群规模为40，最大进化代数为100 代，交叉概率为0.7，变异概率为0.1。

（3）评估指标

单一的指标不能对模型的准确度有较好的评价，本文选取以下四个指标对模型作综合评价，并以此为依据作对比分析：

式中：M为样本点数，y为样本的测试值，为样本预测值，为样本的平均值，其中R2为相关性系数，表示预测值与实测值之间的相关性，该值应用于工程时一般不低于0.8[8]。MAE表示所得结果的偏差性，RMSE表示结果的离散程度，MAPE表示结果的准确性，式（3）～（5）值越小说明模型误差越小，反映出神经网络的预测愈准确。

3 结果分析

分别对标准BP、PCA-BP 与PCA-GA-BP 模型训练的结果与实测值进行对比，如图2 所示。

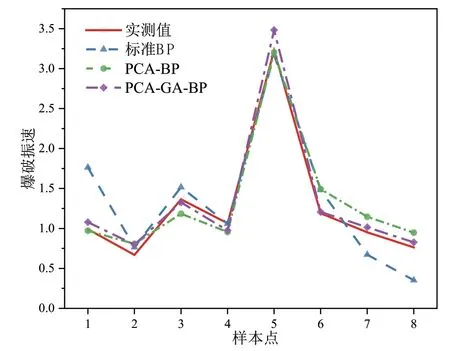
图2 预测值与实测值对比

从图2 中分别比较了几种模型预测的爆破振速与实测值，不难发现标准的BP 神经网络与实测值之间有较大的误差，这是因为未经处理的输入层参数存在着变量间的多重相关性，数据间信息的重叠影响了模型的精确度，使用主成分降维处理后，PCA-BP 模型与实测数据较符合，但受到神经网络的初始权值和阈值的影响，给模型的预测精度优化有了一定的提升空间，当结合遗传算法优化后，相比较于标准BP 和PCA-BP 模型精度有明显的提升，各模型之间的误差评价指标如图3 所示。

图3 各模型之间评估指标比较

标准BP 神经网络在回归效果上对振速的相关系数值为0.793，整体效果一般，降维处理后的PCA-BP 神经网络则为0.951，模型的MAE、MSE、MAPE均在变小，这意味着模型的整体预测可信度在提高，说明降维处理后的数据对于神经网络的非线性能力提升较好，提高了神经网络的稳健性和泛化能力，而对于采用遗传算法优化后的评价指标变化更为明显，MAE从0.258 降至0.104、MSE从0.121 降至0.107、MAPE则从27%降至8%，可见优化后的模型无论在预测精度还是回归效果上都有显著的提升，这说明使用PCA 结合GA 优化BP 神经网络是切实可行，对比起传统的BP 神经网络而言能够更好地对爆破振速作出预测。