影响随机噪声CCA法勘探的关键因素试验研究❋

孟庆生, 李 杨, 王文静, 陈玉红

(1. 中国海洋大学环境科学与工程学院, 山东 青岛 266100; 2. 海洋环境与生态教育部重点实验室, 山东 青岛 266100; 3. 山东省海洋环境地质工程重点实验室, 山东 青岛 266100)

地球表面普遍存在一种微弱的、低振幅的振动,国内学者称之为微动,它随时间、空间而变化,这种变化非常复杂和不规则,而且不可重复。这个意义上讲,它是一种“不受控制的信号”,因而用随机噪声来描述更贴切。地球物理测量技术的最新进展之一就是将随机噪声测量法应用于建筑和结构工程领域[1],但其主要目的不再是单纯的场地土动力学评价、地震反应分析、定量评价场地条件等,而是逐步拓展到工程地震勘察[2-3]、活断层探测、地下水资源调查[4]、地质灾害监测预警[5-6]等方面,可服务于城市轨道交通、水利、铁路、市政等领域。

随机噪声测量方法尚未发展成常规地震方法而被应用或推广,但它是一种基于全新思想的方法,其测量非常简单,操作不需要严格的环境和安全预防措施,可以克服很多传统地球物理技术在某些地区难以实施或不可能实施的难题,特别是在人口稠密的城市或环境敏感地带[7]。这种方法的魅力在于它与常规地球物理方法在思路和手段上的不同,它以信号具有时空平稳性为假设条件,并采用特殊的观测阵列[8],这种差异可能影响到它适用性,也直接导致了随机噪声勘探法虽然已发展近30 年,但在中国工程领域的应用仍处于工程实践研究和推广应用阶段。

本文针对具有发展潜力的随机噪声CCA观测方法,通过现场试验和数值分析,对不同采样率、采样时长、台阵半径和不同应用场景情形下的信号特征进行研究,以期探讨这些因素对探测结果的影响规律,推动随机噪声勘探方法更好地应用。

1 CCA方法及其基本原理

CCA方法是一种使用圆形检波器阵列从随机噪声中计算Rayleigh面波速度的经典算法,该方法源于1957年Aki提出的空间自相关(SPAC)基本理论[9],之后Cho等学者继承并拓展了这一理论,形成了一个新的综合理论框架,即CCA(Centerless Circular Array)方法[10-11]。其简要的基本原理可描述如下。

假定在随机噪声场中部署了半径为r的圆形阵列,并在极坐标系下用Z(t,r,θ)表示任意(r,θ)位置、任意时间t检波器记录的垂向分量。Cho等[11]用Zm(t,r)表示Z(t,r,θ)的傅里叶级数展开(按方位)后的第m阶系数,并定义了如下广义谱密度:

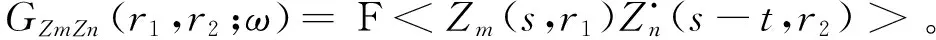
(1)

式中:F代表傅里叶变换;ω为角频率。上式表明广义谱密度可以表示为傅里叶展开系数互相关(或自相关)的傅里叶变换,可以用来评价随机噪声的分布特征及其相关程度。Cho等[11]的最大贡献在于提出了以谱比形式表示方位平均CCA系数,当不存在极化波,即在Rayleigh面波占优势的情形下,有

(2)

由公式(2)可知,一旦从测量数据中获得了谱比ρCCA(r,ω),就可以用该式计算出Rayleigh面波相速度。与SPAC法相比,采用小半径圆形阵列的CCA法可以在更宽的频率范围、更大的深度内给出相速度的合理估计,该方法潜在的应用前景也是本文研究工作的动力所在。

2 试验概况

2.1 试验场地

充分考虑随机噪声的来源及其差异性,按照离海洋远近程度的不同,分别选取东营黄河三角洲(SJZ)、青岛城区(QDS)和济南城区(JNS)作为试验场地。黄河三角洲测试点选在黄河入海口潮间带上,青岛城区测试点位于某校园的一处空地,而济南城区测试点则处在繁华的经十路主干道。三个测试点共同之处在于地表都有一定厚度的松软覆盖层,因其对随机噪声的放大作用,使得能够测量到这些远距离传播的振动。

2.2 试验仪器及试验方案

试验中选用重庆奔腾数控技术研究所生产的WZG-6A型 6通道工程地震仪,台站检波器为威海双丰物探设备股份有限公司生产的PS-2 Hz垂直单分量速度型检波器。试验中共使用6个检波器,其间采用同轴电缆连接方式以保证时间同步性。

实际工作前,先测试各检波器的一致性,在相位、振幅、相干系数等达到一致性要求后,进行数据采集。试验中采用的CCA圆型观测阵列如图1所示,阵列中6个检波器均匀分布在圆周上,圆心位置未安放台站。依据试验目的,设计以下5种试验方案(见表1)。

表1 不同试验目的及其方案

图1 圆形观测阵列图(a)及现场测试照片(b) Fig.1 Map of the centerless circular array(a) and the field test photograph(b)

根据上述方案分别在上述三个测试场地(见图1)进行了随机噪声测量,其中SJZ试验于2021年10月5、17和18日,测试时间均为白天;QDS场地试验从2021年2月28日开始,进行了连续7天的测量,一天中每隔2 h测量一次;JNS场地试验于2021年9月8日夜间完成。

3 结果分析与讨论

根据上述方案,本文获得了各试验场地的随机噪声记录,作为示例,本文仅给出SJZ场地测点的结果(见图2)。由图可见,随机噪声记录是一个非常复杂的波形,其振幅是不确定的和不可重复的,仅从单台站的波形中无法获知随机噪声场的任何信息。

接下来利用公式(1)进行了数据处理,将每个台站的数据按连续的6个区段分组,我们称之为数据块,两个相邻数据块之间有30%～50%的重复段。对于每个台站,取该台站数据中所有段的功率和广义谱密度的平均值,并使用带宽为0.3 Hz的Parzen窗口对其进行平滑处理,最终得到了随机噪声的Fourier谱(FSD)、功率谱密度(PSD)和各台站间的相关系数。通过对这些结果的分析,探讨影响随机噪声测量结果的因素。

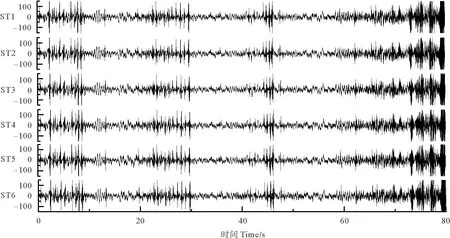
图2 SJZ测点原始记录图

3.1 不同应用场景随机噪声特征

由于随机噪声被认为是自然因素和人为因素共同引起的,我们推测三个场地的观测噪声具有不同的信号特征。为了验证这一点,计算了3个测试点观测数据的Fourier谱并绘制于图3中,图中显示各个通道中从低频到高频均有一定幅度的随机噪声信号,由于图中曲线彼此之间仅略有不同,因而可以认为随机噪声在各个方向传播,每个方向的能量几乎相同。从曲线图的特征上分析,SJZ场地随机噪声在低频段(1.9～7.7 Hz)幅度一致性较好,高频段相对离散,JNS场地高频段(19.0～31.0 Hz)随机噪声幅度一致性优于低频段,而QDS场地随机噪声则在高低频段(低频段为2.0～8.0 Hz,高频段为14.0～20.0 Hz)均具有良好的一致性。结合实际的测量环境,我们分析认为黄河三角洲试验场地因靠近海洋,波浪、潮汐和风等因素可能是主要的噪声源,它们通常表现为低频、长波长,当然也会有航船引起的高频、短波长噪声;济南城区试验场地位于繁华的城市街道,为典型的内陆类型,主要的随机噪声源以工业振动、交通和行人为主,相关噪声成份以高频、短波长为主;而青岛城区试验场地同时受到自然因素(海洋)和人为因素的影响,其相关性噪声出现在更宽的频段。上述分析表明不同的应用场景具有不同的有效频带,而频率是决定随机噪声法勘探深度的关键因素,因而相关结论可用于指导野外施工设计。

((a) SJZ场地; (b) JNS场地和 (c) QDS场地。(a) SJZ site, (b) JNS site and (c) QDS site.) 图3 各测试点Fourier谱

3.2 采样率对观测结果影响

实际振动信号采集过程中,采样率是很重要的参数,采样率的不同会影响采集到噪声信号的质量,甚至于无法从采样后信号中将原始信号恢复出来。对随机噪声这种具有宽频带特征的信号来说,究竟采用何种采样率能取得较好的分辨率,仍然值得探讨。本文选取QDS场地,分别计算0.50、2.0、5.0和20.0 ms四种采样率情形下的Fourier谱(见图4)和相关系数曲线(见图5)。

((a) 0.50 ms; (b) 2.0 ms; (c) 5.0 ms; (d)20.0 ms。) 图4 QDS场地不同采样率时的Fourier谱

综合分析图4和图5中曲线的变化规律,可以发现:(1)频率低于2.0 Hz时,各台站的Fourier谱相对分散,相关性明显较低,而这个频率恰恰对应台站检波器的自然频率;(2)随着采样率的增加,各台站Fourier谱一致性升高,对应的频段范围也逐渐增大,到5.0 ms时最佳(见图4(c)),最高频率达到了22.0 Hz。若以0.95作为评价相关性的下限值,则由图5(a)—(c)也可以看到随着采样率增高,高相关性的频段依次增大,并与Fourier谱反映出的规律完全吻合。但当采样率增大到20.0 ms时,Fourier谱的一致性和相关性均降低且无法获得高频段的噪声信息;(3)图5所有的曲线中,约8～14 Hz频段相关系数陡降,大致对应图4中相同频段曲线的凸起(或凹陷)位置,推断可能是受到瞬态脉冲噪声(如强干扰源)的影响,导致噪声偏离了正态分布特征。

3.3 采样时长对观测结果的影响

CCA方法假设随机噪声具有时间平稳性,将随机噪声视为随机变量并分析其频率分布和相关特性,可以检验这一假设条件的满足程度。试验中针对20.48、40.96和81.92 s三种不同采样时长的台站数据,分析了其功率谱密度和台站间的相关系数特征,以确定不同采样时长台站数据对观测结果的影响。

((a) 0.50 ms; (b) 2.0 ms; (c) 5.0 ms; (d) 20.0 ms。) 图5 QDS场地不同采样率时的相关系数

图6和图7为依据公式(1)和公式(2)计算的QDS场地结果。图中显示周期小于0.08 s(频率大于12.5 Hz)时,三种采样时长的功率谱密度曲线差异均较大,相关性很差;周期0.08～0.50 s(2.0～12.5 Hz)范围内,功率谱密度曲线和相关系数的一致性较好,但相比之下20.48和81.92 s两种采样时长的结果要明显优于40.96 s的结果,这似乎表明了这一影响因素的无规律性;在周期大于0.50 s(频率<2.0 Hz)时,采样时长20.48 s的功率谱密度一致性差,其相关性也低,其它两种采样时长的结果更好一些,但此时采样时长40.96 s的结果要优于81.92 s的结果。根据上述的分析,本文认为:(1)采样时长对观测结果的影响是比较复杂的,这可能是由于随机噪声的复杂性导致信号不满足平稳随机特性,要解决这一问题,需要在数据采集时加强质量控制环节,实时调整采样时长参数以便获得准确的测量结果;(2)较短的采样时长仍然能够获得高质量的噪声数据,这一点对实际的工程应用非常有利。

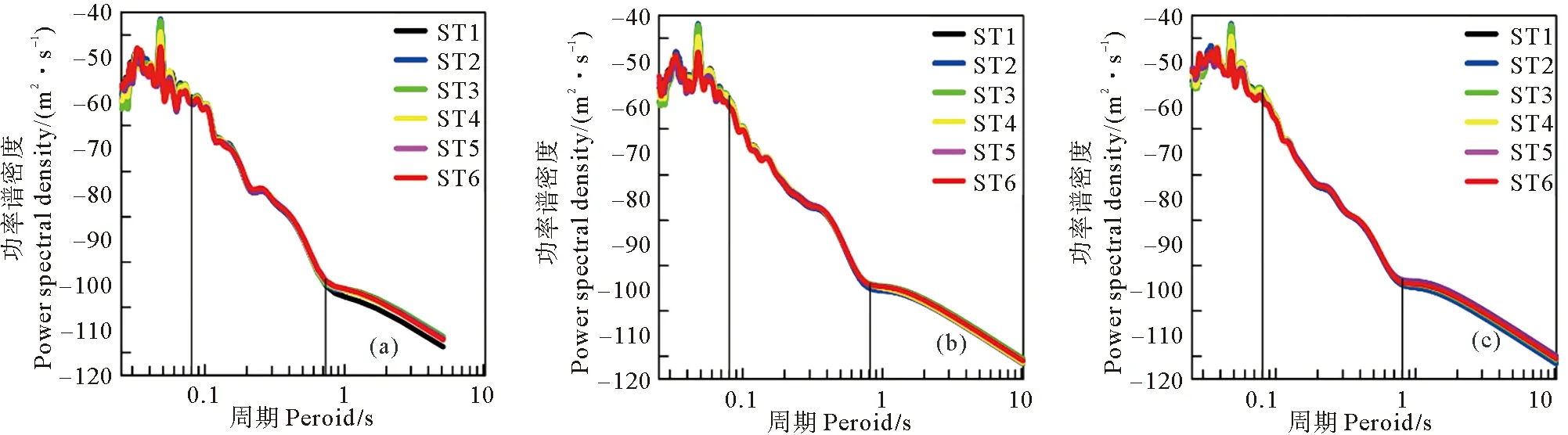
((a) 20.48 s; (b) 40.96 s; (c) 81.92 s。) 图6 QDS测点在不同时长下的功率谱

((a) 20.48 s; (b) 40.96 s; (c) 81.92 s。) 图7 QDS测点在不同时长下相关系数曲线

3.4 台阵半径对观测结果影响

观测阵列的台阵半径是CCA法应用中的重要指标,已有研究证实台阵半径越大探测深度越深,但现在我们关注的是更小的台阵半径是否也可以获得足够的分辨率和稳定性。因为很多已有的工程需求中不具备开展大半径阵列观测的条件,如在地铁隧道超前预报工作中,因空间受限而无法开展大半径阵列观测工作。Cho等通过试验验证了半径5～15 m的小型阵列的适用性[11],接下来采用不同阵列半径的功率谱密度和各台站间随机噪声信号的相关性分析,以获得小阵列半径时CCA测量方法的时空平稳程度,进一步分析半径小于5 m时对观测结果产生的影响。

图8和图9分别为QDS场地1、2和3 m台站半径获得的功率谱密度曲线和相关系数曲线。对比三种台阵

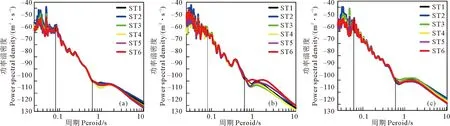
((a) 1 m; (b) 2 m; (c) 3 m。) 图8 QDS场地在不同台阵半径下的功率谱

((a) 1 m; (b) 2 m; (c) 3 m。) 图9 QDS场地在不同台阵半径下的相关系数曲线

半径的结果,表明周期0.08～0.50 s(2.0～12.5 Hz)范围内,功率谱密度和相关性均较好,而在其它频率段一致性较差。且随着台阵半径的降低,其相关性依次升高,当台阵半径为1 m时,无论是功率谱密度还是各台站间观测数据的相关系数(大于0.95)都是最佳的,从而表明了更小台阵半径仍能保证随机噪声的时空平稳性。

4 结论

在东营黄河三角洲、青岛城区和济南城区三处地点开展不同采样率、采样时长、台阵半径和不同应用场景的噪声观测工作,得到以下主要结论:

(1)不同应用场景中,随机噪声展现出不同的有效频带,从而决定了有效的勘探深度,对这一特性的研究将有助于指导施工设计。

(2)采样率会影响观测精度,在本文的工作中证实5.0 ms的采样率具有最佳的能量一致性和高相关性,对应的有效频率范围也最宽,但试验结果也证实采样率并非越大越好,这可能需要测量前的试验来确定这一最佳参数。

(3)较短的采样时长可以获得高质量噪声数据,这有利于提高工作效率,但受限于随机噪声复杂性,需要通过现场试验获得最佳采样时长。

(4)更小台阵半径仍能保证随机噪声的时空平稳性,有利于拓展应用领域。小于5 m的观测半径同样具有时空平稳性,可以获得高质量的测量数据,有利于解决特殊环境下的随机噪声测量施工。

(5)实际应用中应注意避免短时的强干扰源或持续性强干扰源,这可能导致噪声偏离正态分布,影响数据质量。