基于离散元法的颗粒-气泡间相互作用行为模拟研究

陈有轩,张志军

(中国矿业大学(北京) 化学与环境工程学院,北京 100083)

浮选是一种实现细粒矿物及煤炭分选提质的高效分选方法,其原理是利用不同矿物颗粒表面物理化学性质的差异实现有用矿物与脉石矿物的选择性分离,疏水性矿物颗粒能够与气泡黏附并形成稳定的颗粒-气泡结合体上浮至矿浆表面成为精矿产品,亲水性颗粒因不能与气泡黏附而继续停留在矿浆中并随尾矿排出[1]。颗粒-气泡间相互作用过程可分为3个子过程:① 颗粒-气泡碰撞过程;② 颗粒-气泡黏附过程;③ 非稳定黏附颗粒脱落过程[2-3]。这3个子过程共同决定气泡对颗粒的捕获效率。颗粒-气泡的碰撞过程主要取决于浮选槽内流体力学因素的影响以及颗粒和气泡的尺寸、数量的影响[4],且与流场分布息息相关[5]。

颗粒-气泡的黏附过程又可分为3个子过程:颗粒-气泡间液膜薄化至临界液膜破裂厚度;液膜破裂形成三相接触线;三相接触线扩展形成稳定的接触周边[6]。颗粒从气泡表面脱落过程受到浮选槽内流体力学因素的支配,在颗粒-气泡结合体上浮的过程中,过强的流体扰动会克服颗粒-气泡间的毛细管力,致使颗粒脱落[7]。

颗粒-气泡间相互作用行为的试验研究大多数在宏观尺度下进行且以颗粒沉降法[8-9]为主。VAZIRI等[10]研究了颗粒形状以及表面粗糙度对颗粒-气泡间相互作用的影响,试验发现,玻璃微珠的临界碰撞角最大,腐蚀后的玻璃微珠次之,腐蚀后的不规则玻璃颗粒最小。LECRIVAIN等[11]研究了玻璃纤维与气泡间的相互作用,发现玻璃纤维与气泡之间的碰撞角在小于30°时,玻璃纤维在与气泡黏附时会发生强黏附,即玻璃纤维沿长轴方向与气泡相切,而当碰撞角大于30°时会发生弱黏附,即玻璃纤维沿短轴方向与气泡相切。NGUYEN和EVANS[12-13]利用Milli-Timer试验装置研究玻璃微珠与气泡间的相互作用,观察到了玻璃微珠在气泡表面滑动时会有一个“陷入”现象,这是因为液膜薄化至临界液膜厚度时,玻璃微珠刺破液膜形成三相接触线。卓启明等[14-15]采用自行搭建的颗粒与气泡碰撞、黏附行为测量装置研究颗粒-气泡间相互作用时发现:煤颗粒在接近气泡表面时会沿气泡上半球做绕流运动,运动轨迹发生改变。当煤颗粒与气泡发生碰撞时,颗粒速度降至最低。发生碰撞后,煤颗粒随即在气泡表面滑动,颗粒滑动速度逐渐增加,当颗粒到达气泡“赤道”位置时速度达到最大值,跨过“赤道”后,滑动速度逐渐降低,最终停留在气泡底部。

目前对颗粒-气泡间黏附过程的机理研究还不透彻。一方面是颗粒和气泡的表面物理化学性质以及溶液化学性质等因素均能影响黏附过程且每一个因素都不易量化、难以用数学模型表达。另一方面是在黏附过程中,颗粒-气泡间液膜厚度大多在微米以内,整个过程持续的时间约为几十毫秒且气泡表面会在受到外力的作用时发生形变[16]。这两方面均给黏附过程的试验研究带来了巨大挑战,因此也约束了科研人员对颗粒-气泡间相互作用行为的进一步认识。

近年来数值模拟技术获得长足进步,因此通过计算机数值模拟的方法研究颗粒-气泡间相互作用成为了可能[17]。在颗粒-气泡间相互作用的模拟研究中,主要有2类方法:第Ⅰ类为多相流方法,由于该方法未考虑颗粒-气泡之间的相互作用力,不适合模拟颗粒与气泡的黏附过程,因此该方法主要用于研究颗粒-气泡间的碰撞过程[18]。第Ⅱ类为离散元法,由于离散元法(DEM)是根据力位移定律进行迭代计算的,所以其能较好解决颗粒-气泡间的相互作用力以及气泡的变形等难点。MAXWELL等[19]基于离散元法搭建了颗粒群-固定气泡间相互作用的模型,研究了颗粒粒度、颗粒数量、颗粒-气泡间疏水作用力强度对颗粒-气泡碰撞的影响以及颗粒在气泡表面的滑动时间。MORENO-ATANASIO[20]对比研究了单指数、双指数、幂函数型等3种疏水作用力模型对气泡捕获颗粒的影响。GAO等[21]采用单指数型疏水作用力公式研究了疏水作用力对颗粒-气泡间相互作用的影响,发现当λ(衰减长度)小于10 nm时,气泡捕获的颗粒数量与疏水作用力强度无关。而对于λ在10～500 nm内,捕获效率随着疏水作用力和λ的增加而增加。

综上所述,由于颗粒-气泡间黏附过程的复杂性和微观性给宏观尺度下的相关试验研究提出了很大挑战,并且离散元法(DEM)能较好地解决颗粒-气泡间相互作用力和气泡形变等难点。因此笔者在颗粒-气泡间力学理论的基础上结合离散元法(DEM)对不同密度级的球形煤颗粒与气泡间的相互作用行为进行了模拟研究。

1 模拟系统

1.1 模型描述

模拟系统的三维示意如图1所示。在静止的水环境中,气泡被固定在坐标原点O处,颗粒在距离气泡中心O上方3Rb(Rb为气泡半径)处的水平面上沿X轴正方向依次生成并释放,颗粒每次生成的位置都较上一次的生成位置向X轴正方向多出一定的距离。如此循环直至颗粒在X轴某一位置释放时颗粒不能被气泡捕获。在本模拟中将颗粒接近气泡过程中,颗粒速度达到最小值处的位置定为碰撞点,气泡中心与碰撞点的连线与Z轴正方向的夹角定为碰撞角(φ)。

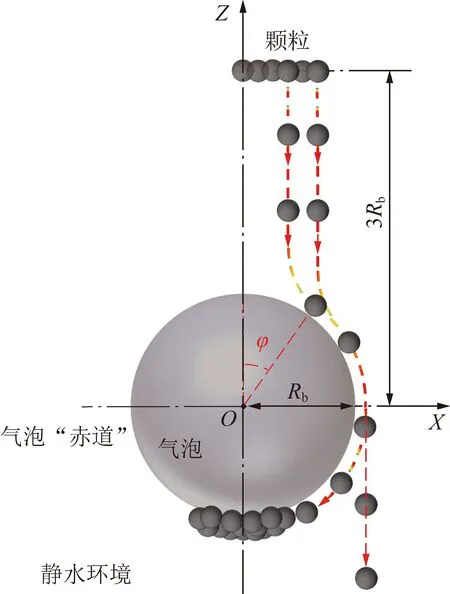
图1 模拟系统示意Fig.1 Schematic diagram of simulation system

颗粒-气泡间的力学模型示意如图2所示,根据各力的作用范围和性质不同可分为2类:颗粒-气泡接触前作用力(范德华作用力、静电作用力、疏水作用力)和颗粒-气泡接触后作用力(毛细管力、静水压力、拉普拉斯压力、离心力),重力、浮力、流体阻力在整个模拟过程中都一直存在。

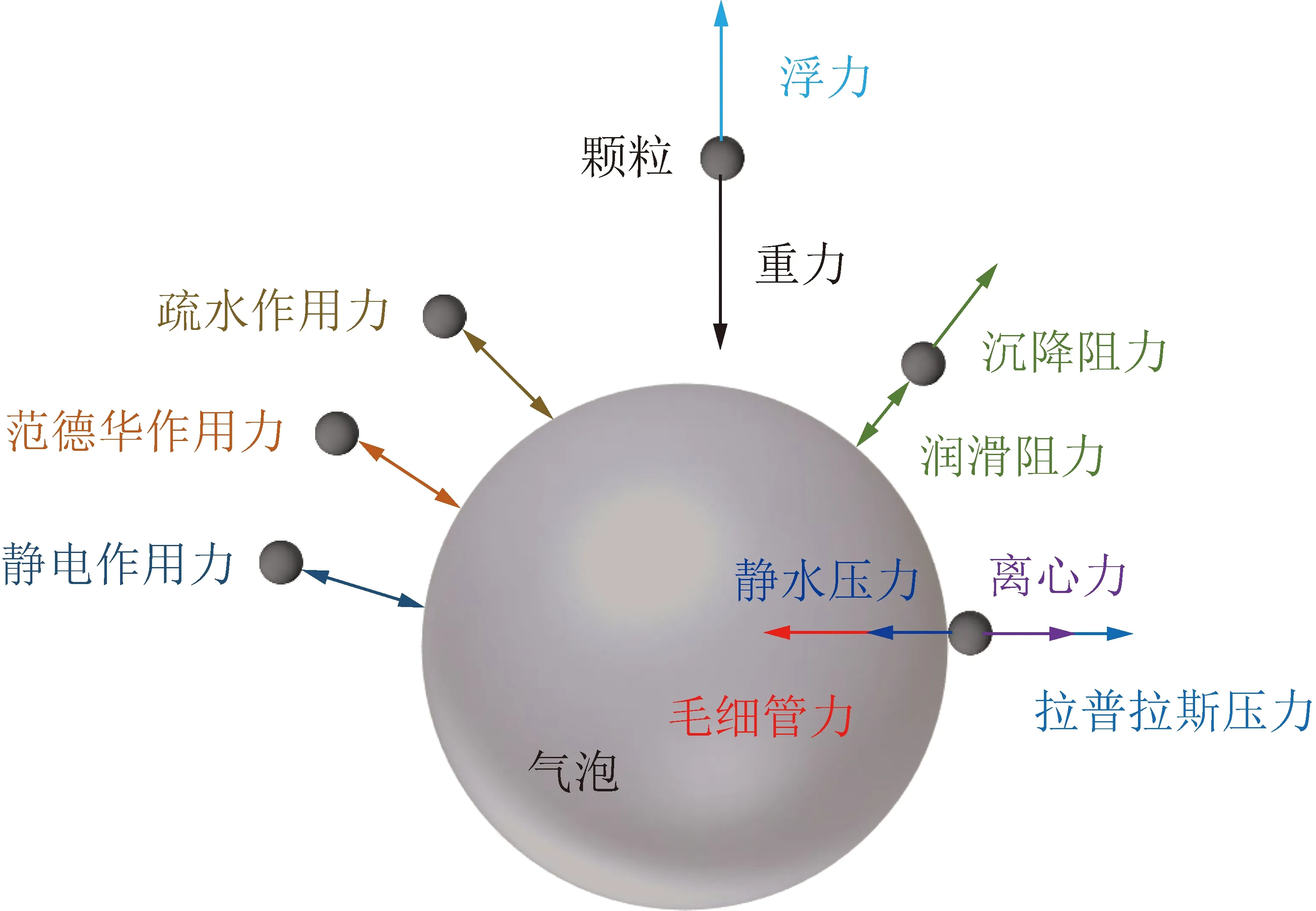
图2 颗粒-气泡间力学模型示意Fig.2 Schematic diagram of particle-bubble mechanical model

1.2 离散元法(DEM)与运动方程

离散元法(DEM)是CUNDALL[22]1971年在研究岩土力学问题时首次提出,其基本思想是把研究对象离散为刚性元素的集合,每个元素都具有相应的质量、转动惯量和接触参数等物理参数,并且每个刚性元素都满足牛顿第二定律,用时间步迭代的方法求解各刚性元素的运动方程,从而得到研究对象的整体运动形态。

本次模拟使用颗粒流程序(Particle Flow Code,PFC)软件来模拟颗粒-气泡间相互作用行为。通过添加额外作用力的方式将所需的各种作用力的公式添加到接触模型中,该软件会在每个时间步长内更新颗粒和气泡之间的距离,从而计算更新颗粒所受到的各种相互作用力的大小,最后通过力-位移定律得到颗粒的加速度、速度和位置等信息,其运动方程为

(1)

式中,m为颗粒质量;r为颗粒的位移;t为时间;FG、FB、FR、FBC、FAC分别为颗粒所受重力、浮力、流体阻力、颗粒-气泡接触前作用力、颗粒-气泡接触后作用力。

1.3 颗粒-气泡接触前作用力

扩展的DLVO(Derjaguin-Landau-Verwey-Overbeek)理论即EDLVO理论[23]认为,在颗粒与气泡相互作用的过程中存在3种作用力,即:范德华作用力、静电作用力和疏水作用力。

1.3.1 范德华作用力

范德华作用力FV是一种弱碱性的电性吸引力其存在于中性分子或原子之间,也是颗粒与气泡等宏观物体间一种重要的相互作用力,不同物体间因具有不同形状和大小而导致其范德华作用力不同[24]。

假设颗粒和气泡的半径分别为Rp、Rb的球体,则范德华作用力公式为

(2)

式中,A132为颗粒和气泡在介质(水)中的Hamaker常数;h为球形颗粒表面与气泡表面之间的最短距离。

在气固液三相体系中,Hamaker常数A132可由式(3)计算:

(3)

式中,A11、A22、A33分别为颗粒、气泡、介质(水)在真空中的Hamaker常数。

煤泥浮选体系中一些物质在真空中的Hamaker常数见表1,根据表1并结合式(3)可以计算出在水溶液中煤颗粒和气泡在水介质中的Hamaker常数A132为-1.050 8×10-20J,因此在煤泥浮选体系中煤颗粒-气泡间的范德华作用力为斥力。

表1 物质在真空中的Hamaker常数[25]

随着煤的密度级增加,其中无机矿物质组分在煤中比例也逐渐增加,并且煤中无机矿物质组分在真空中的Hamaker常数通常大于煤在真空中的Hamaker常数。根据Hamaker常数的成对可加性[26]可知随着煤的密度级增加其在真空中的Hamaker常数也逐渐增加,因此根据该性质可近似得到各密度级煤在真空中Hamaker常数,见表2。

表2 不同密度级煤在真空中的Hamaker常数

1.3.2 静电作用力

颗粒-气泡间的静电作用力公式有多种不同的形式[27-28],本模拟采用的静电作用力FE为

(4)

(5)

(6)

式中,ε为介质(水)的介电常数;к为德拜长度的倒数;ψ01、ψ02为颗粒和气泡的表面电位,可用Zeta电位近似代替,V。

1.3.3 疏水作用力

疏水作用力公式主要有3种形式:单指数型、双指数型和幂函数型[29]。目前关于疏水作用力还没有普遍认同的形式,因此本模拟选取幂函数型疏水作用力FH公式,该计算公式为

(7)

(8)

式中,K131、K232、K132分别为颗粒和颗粒、气泡和气泡、颗粒和气泡在介质(水)中的疏水作用力常数,J。

此外,上述3种作用力均在h趋于无穷小时其绝对值趋于无穷大,显然这是不正确的,因此为了防止计算出错所以在模拟中加入了截至距离(0.5 nm)[19],即当h<0.5 nm时,认为颗粒与气泡已经发生了接触,这3种作用力将不再考虑,停止计算。

1.4 颗粒-气泡接触后作用力

当颗粒成功的黏附在气泡上,将其定义为颗粒-气泡结合体,其几何示意如图3所示。

图3 颗粒-气泡结合体示意[30]Fig.3 Geometry of a particle-bubble aggregate[30]

1.4.1 毛细管力

毛细管力是颗粒和气泡之间最主要的黏附力,矿物颗粒在气泡表面的黏附很大程度上取决于毛细管力。毛细管力与接触角、表面张力、三相接触线有关,同时毛细管力可能是浮选过程中最重要的力[31]。毛细管力Fcap的计算公式为

Fcap=2πRpσsinαsin (θ-α)

(9)

式中,σ为液体表面张力,N/m;θ为接触角,(°);α为气泡中心与三相接触线的连线与竖直方向的夹角,(°)。

1.4.2 总压力

由于颗粒-气泡结合体存在弯曲的气-液界面,因此在气泡内部会存在拉普拉斯压强,其表达式为

(10)

式中,Δp为拉普拉斯压强。

又因为气泡为球形,所以R1=R2=Rb,则式(10)可化简为

(11)

总压力Fp是作用在颗粒上的拉普拉斯压力和静水压力之差。静水压力的作用是维持颗粒黏附在气泡上,而拉普拉斯压力的作用是促使颗粒从气泡上脱附。静水压力与拉普拉斯压力的竞争决定了总压力的大小和方向,也决定了其最终的作用效果。作用在三相接触平面上的静水压力Fh、拉普拉斯压力Fl、总压力Fp的公式分别为

(12)

(13)

(14)

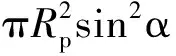
一般而言,拉普拉斯压力远大于静水压力,因此颗粒所受的总压力为脱附力。

1.4.3 离心力

当颗粒被气泡捕获时,颗粒会在重力、毛细管力等力的共同作用下沿气泡表面做圆周运动,因此会产生离心力,离心力Fd计算公式为

(15)

式中,ρp为颗粒的密度;bm为离心加速度,m/s2。

当颗粒与气泡黏附后,颗粒陷入气泡的深度受颗粒表面性质、颗粒和气泡的尺寸、溶液化学条件等的共同影响,没有固定值,约占颗粒和气泡纸直径之和的2%[32]。通过陷入深度可计算出α约为17.06°,进一步计算可知毛细管力比总压力大了约2个数量级,因此总压力相对于毛细管力可以忽略不计,所以在本模拟编写颗粒-气泡间力学模型时只考虑了毛细管力和离心力。

1.5 流体阻力

1.5.1 沉降阻力

当矿物颗粒尺寸微小或矿物颗粒相对于介质的运动速度较小,且形状又易于流体绕流,附面层没有分离时,摩擦阻力占优势,压差阻力可忽略(Re≤1),摩擦阻力可用斯托克斯公式计算[33],即

Fdrag=6πηRpv

(16)

式中,η为介质的动力黏度,Pa·s;v为矿粒的相对速度,m/s。

1.5.2 润滑阻力

在颗粒接近气泡过程中,由于颗粒-气泡间的水分子被不断排开,因此气泡会对颗粒施加一个反作用力(润滑阻力),宏观表现为颗粒在接近气泡表面时会有一个绕流现象,运动轨迹发生改变。当前使用较为普遍的排液模型主要有3种:Sterfan-Reynolds平坦膜模型、Taylor模型和Stokes-Reynolds-Young-Laplace(SRYL)模型[34]。由于颗粒-气泡表面间距在一个颗粒直径范围内时,Taylor模型与试验结果较为吻合[35],因此本模拟中选用Taylor模型来计算润滑阻力,计算公式[36]为

(17)

式中,vr为颗粒速度在颗粒与气泡中心连线上的分量,m/s。

1.6 模拟参数

本次模拟中气泡的直径为1 mm,气泡的表面电位为-45 mV。颗粒直径为0.1 mm,颗粒性质选取了-1.3,1.3～1.4,1.4～1.5,1.5～1.6,1.6～1.7,+1.7 g/cm3等6个密度级煤样的性质。具体模拟参数见表3。颗粒性质见表4,其中各密度级煤颗粒的Hamaker常数可根据表1、2中的数据结合式(3)计算得到,疏水作用力常数K132的取值参考Yoon的试验结果[31]。

表3 模拟参数

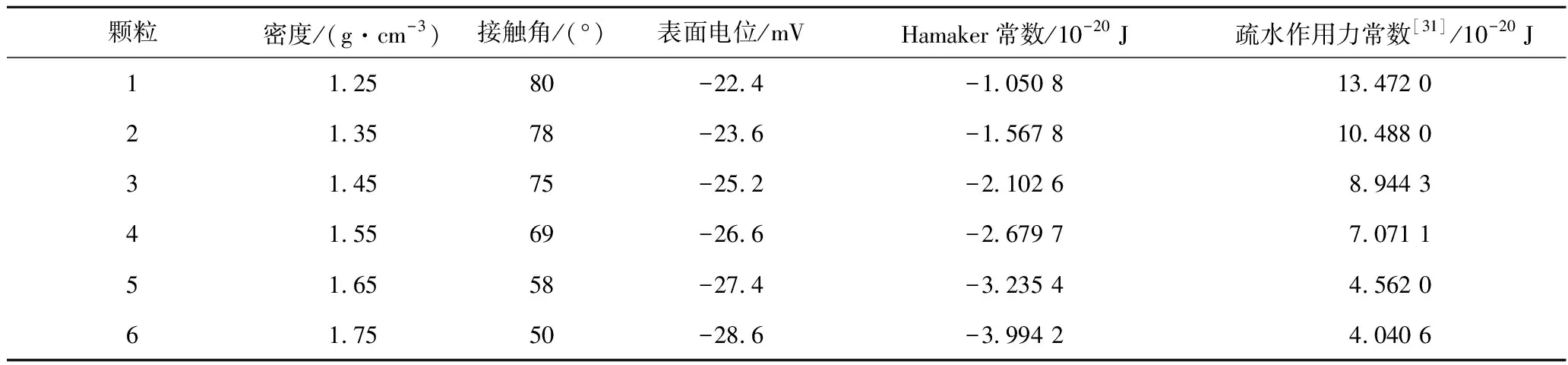
表4 颗粒性质参数

2 模拟结果与讨论

2.1 颗粒-气泡间相互作用行为分析

图4为一个典型颗粒(密度1.45 g/cm3,粒度0.1 mm,碰撞角40.71°)与气泡的相互作用行为,可分为5个阶段:① 自由沉降阶段,颗粒在经过短暂的加速后达到自由沉降末速,然后开始做匀速沉降运动;② 绕流运动阶段,颗粒在到达气泡表面附近时,因为颗粒-气泡间的水分子被不断排开,所以在此过程中气泡会对颗粒产生一个由气泡指向颗粒的阻力(润滑阻力)导致颗粒在气泡表面做绕流运动,运动轨迹发生改变;③ 颗粒在液膜上滑动阶段,颗粒与气泡发生碰撞后,颗粒在各相互作用力以及重力等力的共同作用下,颗粒随即在颗粒-气泡间的液膜上滑动;④ 液膜破裂形成三相接触线(TPC)阶段,当颗粒-气泡间液膜厚度薄化至临界液膜厚度时,颗粒刺破液膜形成三相接触线以及三相接触线扩展至稳定状态;⑤ 伴随TPC滑动阶段,颗粒在与气泡形成三相接触线的基础上,在毛细管力、拉普拉斯压力、浮力、静水压力、离心力、重力的共同作用下,颗粒继续沿气泡表面向下滑动,最终停留在气泡底部。

颗粒-气泡间相互作用行为的模拟结果与NGUYEN和EVANS[12]利用Milli-Timer试验装置观察到的玻璃微珠-气泡间相互作用行为的各个阶段较为吻合,其试验结果如图5所示。

此外,虽然上述5个阶段均存在于各个密度级颗粒与气泡相互作用中,但是由于各密度级煤颗粒的表面性质存在着很大的差异,因此导致各个阶段持续的时间会有所不同。

图6为颗粒(密度1.45 g/cm3,粒度0.1 mm,碰撞角40.71°)速度变化曲线。①A—B段为自由沉降阶段:该阶段颗粒在经过短暂的加速后便达到自由沉降末速(2.43 mm/s),然后以该速度接近气泡。②B—C段为绕流运动阶段:颗粒在与气泡碰撞前,颗粒会沿气泡上半球做绕流运动,此过程中颗粒速度的大小和方向均会发生改变,颗粒速度从2.43 mm/s降低至1.47 mm/s,降低了约40%,C点为碰撞点。③C—D段为颗粒在液膜上滑动阶段:碰撞后颗粒随即沿气泡表面上的液膜滑动且滑动速度不断增加,滑动速度从1.47 mm/s增加至1.96 mm/s。④D—E段为液膜破裂形成三相接触线(TPC)阶段:颗粒滑动到气泡表面某一位置时(此时颗粒-气泡间的间距为150.14 nm),颗粒的滑动速度骤然下降,从1.96 mm/s降至0.87 mm/s。这是因为颗粒与气泡间的液膜厚度达到临界液膜厚度后(150.14 nm)液膜破裂并形成三相接触线。⑤E—F段为伴随TPC滑动阶段:颗粒在形成三相接触线的基础上继续滑动且滑动速度逐渐增加,当颗粒到达气泡的“赤道”位置附近时,颗粒滑动速度达到最大值2.42 mm/s,颗粒在经过气泡“赤道”位置后,颗粒的滑动速度逐渐降低,最终停留在气泡底部。另外对E—F段分析可知:颗粒在气泡表面的滑动速度近似关于气泡“赤道”对称,这与VERRELLI等[37]观测的试验结果相吻合,即颗粒滑行速度在气泡“赤道”两侧并非完全对称。

颗粒速度的模拟结果与卓启明[38]试验测得的煤样颗粒(粒级为0.15～0.10 mm,密度级为1.4～1.5 g/cm3,碰撞角为41.95°)速度变化规律相吻合,其试验结果如图7所示。试验结果中颗粒自由沉降末速为2.97 mm/s,而模拟结果为2.43 mm/s并且在颗粒与气泡碰撞前,试验结果中颗粒速度降低了约33%,而模拟结果降低了约40%,这是因为其试验中采用的煤颗粒为不规则颗粒,而模拟采用的颗粒为球形颗粒,因此2者的自由沉降末速和速度变化会存在一定的差异。此外其试验结果中没有体现颗粒与气泡间的液膜破裂形成三相接触线以及三相接触线扩展这一过程。分析认为,可能是因为该过程时空尺度较小,导致其开发的多目标追踪软件未能捕捉到这一过程。

2.2 临界碰撞角分析

临界碰撞角的定义为:颗粒与气泡的碰撞角(φ)若不大于临界碰撞角(φc)则颗粒会被气泡捕获,否则颗粒不会被气泡捕获。如图8所示,以密度为1.45 g/cm3、粒度为0.1 mm、临界碰撞角为45.30°的颗粒为例,当φ1≤φc时颗粒会被捕获,而当φ2>φc时颗粒不会被气泡捕获。

为了探索临界碰撞角与密度的关系,模拟得到了密度级为-1.3、1.3～1.4、1.4～1.5、1.5～1.6、1.6～1.7、+1.7 g/cm3,粒度为0.1 mm的颗粒与气泡的临界碰撞角。模拟结果如图9所示(蓝色曲线),随着颗粒密度的增加,临界碰撞角从50.77°降至31.93°。该模拟结果与卓启明等[14]的试验结果变化趋势相符合,其试验结果如图9所示(红色曲线)。将2者对比分析可知:随着颗粒的密度级从-1.3 g/cm3增加至+1.7 g/cm3,模拟结果的临界碰撞角比试验结果大3.63°～6.68°。这是因为在模拟和试验中对临界碰撞角的定义不同,试验中将临界碰撞角定义为颗粒捕获概率为50%时所对应的碰撞角,这是一个概率值而非临界值。因此模拟中的临界碰撞角要比试验结果大一些。

图9 临界碰撞角与密度Fig.9 Critical collision angle and density

分析认为,对于同一品种和产地的煤样,其密度差异主要取决于有机质和无机矿物质在煤中的比例且无机矿物质的密度要高于有机质。有机质的主体为缩合芳香核,缩合芳香核的化学性质稳定不活泼,因此煤的主要表面是疏水的。无机矿物质中多数矿物具有一定的极性,因而使煤表面部分具有亲水性[33]。随着颗粒密度的增加,无机质在煤中的比例也随之增加,因此煤的亲水性逐渐增加,疏水性逐渐减小,这导致由芳香核等疏水的有机质产生的疏水作用力逐渐减小,颗粒-气泡间液膜薄化、破裂形成三相接触线越来越困难,颗粒更难黏附在气泡上。最终表现为:颗粒的密度级从-1.3 g/cm3增加至+1.7 g/cm3,而其临界碰撞角从50.77°降低至31.93°。

2.3 捕获概率分析

当颗粒-气泡间的碰撞角为临界碰撞角时,此时颗粒的释放位置与Z轴之间的水平距离为临界碰撞半径(Rc),临界碰撞半径示意如图10所示。

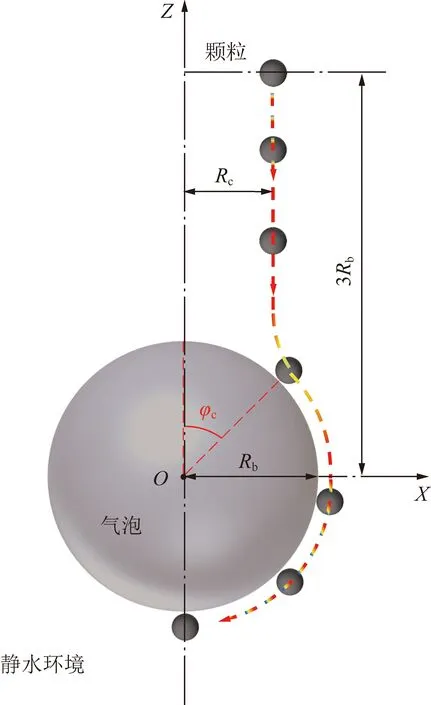
图10 临界碰撞半径示意Fig.10 Schematic diagram of critical collision radius

由于本次模拟中毛细管力远大于颗粒所受的脱附力,即颗粒只要被气泡捕获就不会脱附。因此根据气泡捕获颗粒概率公式[31]和碰撞概率[39]计算可得各个密度级颗粒的捕获概率为

Ecap=EcEa(1-Ed)

(18)

(19)

式中,Ecap、Ec、Ea、Ed分别为捕获概率、碰撞概率、黏附概率、脱附概率。

捕获概率与密度的关系如图11所示,随着颗粒密度的增加,气泡对颗粒的捕获概率从51.74%降低至22.04%。分析认为,随着颗粒密度的增加,颗粒的接触角和疏水性逐渐减小,颗粒-气泡间的疏水作用力也逐渐减小,导致颗粒-气泡间的吸引力越来越小,颗粒越来越难黏附在气泡上。虽然密度的增加会使颗粒的沉降末速和动能增大,使其更容易刺破颗粒-气泡间的液膜并被气泡捕获,但是颗粒因沉降末速增大而增加的动能对颗粒-气泡间相互作用行为的影响远不及颗粒-气泡间的疏水作用力的影响。因此从该模拟结果也可以看出疏水作用力是促使颗粒-气泡黏附的主要因素。

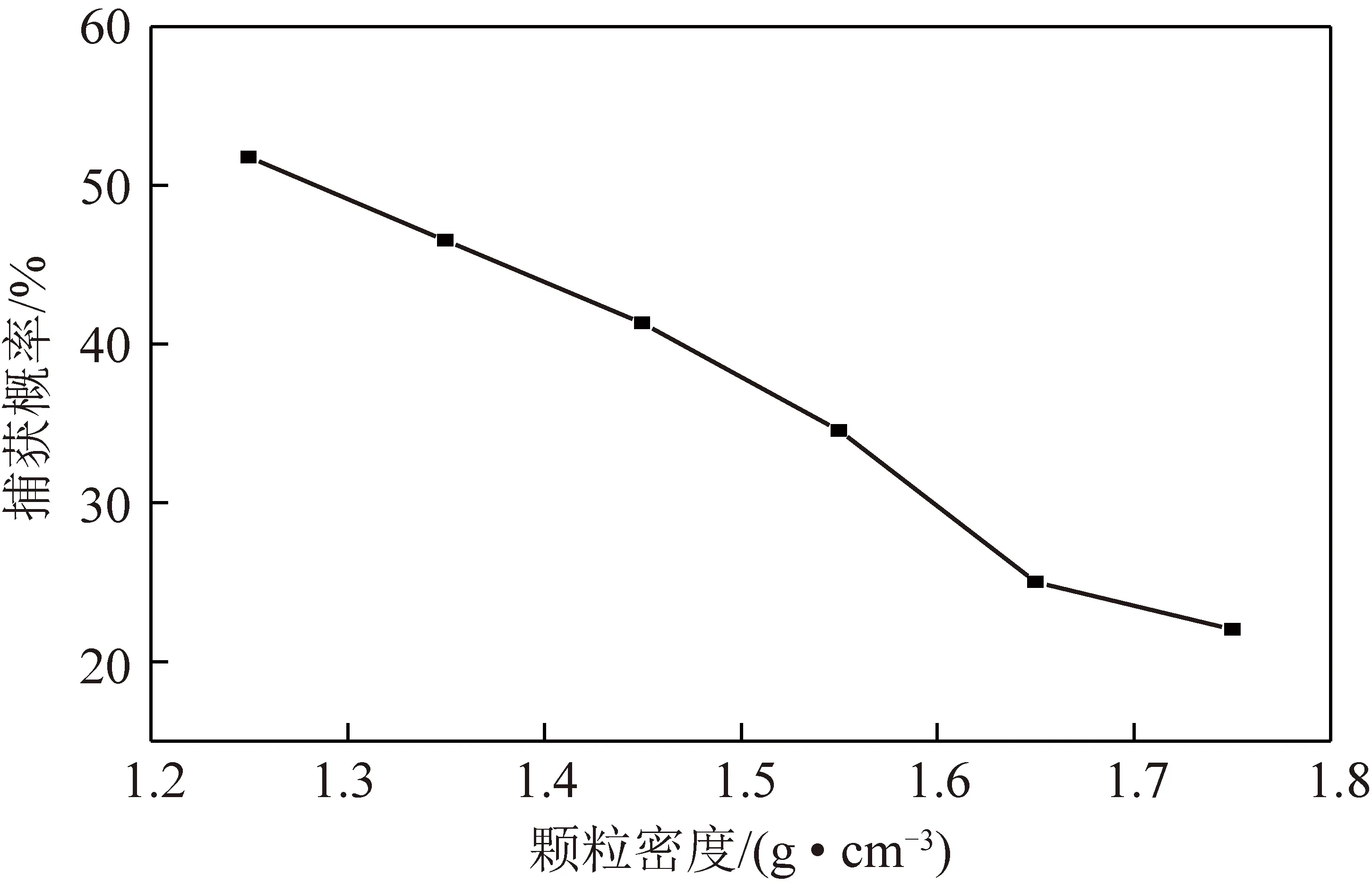
图11 捕获概率与密度Fig.11 Capture probability and density

3 结 论

(1)颗粒以自由沉降末速接近气泡,在到达气泡表面时颗粒会做绕流运动,颗粒运动轨迹发生改变,当颗粒与气泡发生碰撞时其速度降至最低。颗粒-气泡发生碰撞后,颗粒随即在气泡表面滑动,滑动速度先是逐渐增加,然后急速下降,再然后又继续增加。当颗粒到达气泡“赤道”位置附近时速度达到最大值,经过气泡“赤道”后颗粒速度逐渐降低,最终停留在气泡底部。颗粒在气泡表面滑动过程的速度变化近似关于气泡“赤道”对称。

(2)颗粒的密度级从-1.3 g/cm3增加至+1.7 g/cm3时,颗粒的临界碰撞角从50.77°降低至31.93°。

(3)颗粒的密度级从-1.3 g/cm3增加至+1.7 g/cm3时,气泡对颗粒的捕获概率从51.74%降低至22.04%。