概率校准方法的脑电信号分类算法研究

丁胜　吴全玉　孙健　潘玲佼　陶为戈

摘 要：脑机接口技术是很多学科融合的前沿研究方向，脑电信号分类的准确率是限制脑机接口系统实现的难题之一。针对脑电信号分类准确性问题，采用两种概率校准方法Platt Scaling和Isotonic Regression。首先对预处理后的运动想象脑电数据利用功率谱密度提取脑电频域特征，使用主成分分析算法进行特征降维。其次选择逻辑回归和支持向量机构建分类预测模型，使用上述两种概率校准方法进行模型校准。最后，选用ROC曲线下的面积AUC、Brier得分和可靠性曲线评估校准模型的性能，并且绘制交叉验证学习曲线，观察模型在不同数据量下的拟合效果，以及模型的泛化能力。在BCI竞赛IV Datasets 2a脑电数据集上进行实验验证，结果表明，概率校准的方法能够对模型预测输出结果进行有效校准。

关键词：运动想象；概率校准；功率谱密度；逻辑回归；支持向量机

中图分類号：TP18；TP301.6  文献标识码：A  文章编号：1673-260X（2023）04-0011-05

1 引言

脑机接口（Brain-Computer Interface，BCI）是一种不利用外周神经和肌肉，由大脑完成控制命令输出的与外界进行通讯的新方式[1，2]，已在神经康复、生物医学及生活娱乐等领域被广泛研究。运动想象（Motor Imagery， MI）是BCI中的一个重要实验范式，这是一种特殊的心理表象类型[3，4]，人进行运动想象，通过BCI可以实现单独操纵设备[5]。然而脑电信号（Electroencephalogram，EEG）具有复杂，时变，非线性等特点[6]，使得挖掘到有效地脑电信号存在很大的困难，因此，研究如何利用算法对脑电信号进行准确分类显得非常重要[7]。

经典的机器学习算法发展时间长，且具有成熟的数学理论基础，常被用于运动想象脑电信号的分类。许多研究学者对脑电信号分类算法进行一些改进。Shi等[8]采用改进的松鼠搜索算法优化支持向量机的参数，提高了模型的分类精度。Miao等[9]在朴素贝叶斯（Naive Bayesian，NB）基础上提出加权朴素贝叶斯（Weighted NB，WNB），对多个时频特征进行加权，得到不错的分类结果。

然而许多分类算法的预测输出值并不是真正的概率输出，即具有一定的偏差[10]，在实际应用场景中可能会导致一些严重的后果。例如支持向量机（Support Vector Machines，SVM）算法，先寻找让边际最大的决策边界，然后计算测试样本点到决策边界的距离来判定该样本属于哪一类，但是大部分样本点都徘徊在决策边界附近，模型很容易做出错误的判断，只有离决策边界较远的样本才有很高的置信度，所以说SVM是一个“极度不自信”的算法。即使是NB这种真正的概率算法，也会存在有偏的预测。NB产生的分数通常太过极端[11]，概率分布存在两边高，中间低的现象。因此NB模型无法产生准确的概率估计[12]，是一个“过分自信”的算法。特别当测试样本的特征之间并不是条件独立时，朴素贝叶斯分类器输出的概率估计也是存在偏差的。

概率校准的方法可以将有偏差的概率输出结果进行校准。概率校准是指寻找一个校准函数，将初始预测映射为更加精确的后验概率[13]。使用概率校准的方法不仅将非概率分类器的输出转化为概率类型，而且也对概率分类器的结果进一步提升[14]。目前比较可靠的两个概率校准方法为Platt Scaling[15]和Isotonic Regression[16]。

本文选择支持向量机和逻辑回归（Logistic Regression，LR）作为预测模型，引入上述两种概率校准的方法，将模型在第四届BCI竞赛2a数据集上进行验证，结果显示，概率校准后的模型比原始模型有更好的表现。

2 数据集和方法

2.1 数据集

试验数据来源于2008年第四届国际BCI竞赛Datasets 2a数据集[17]。该数据集一共记录了9名受试者（A01，A02，A03，A04，A05，A06，A07，A08，A09）关于左手、右手、双脚和舌头四种不同的运动想象任务，每名受试者在不同的日期记录两次实验。本文只对左右手两类任务进行分类，每个受试者的数据由两个部分组成，一部分用于训练，另一部分用于测试，每个部分都包含了144次试验，每次试验持续7.5秒。所有数据均是通过分布在头部的25个Ag/AgCl电极记录的，采样频率为250Hz，并对采集EEG信号进行0.5Hz-100Hz带通滤波。具体细节参考https：//www.bbci.de/competition/iv/。

2.2 预处理

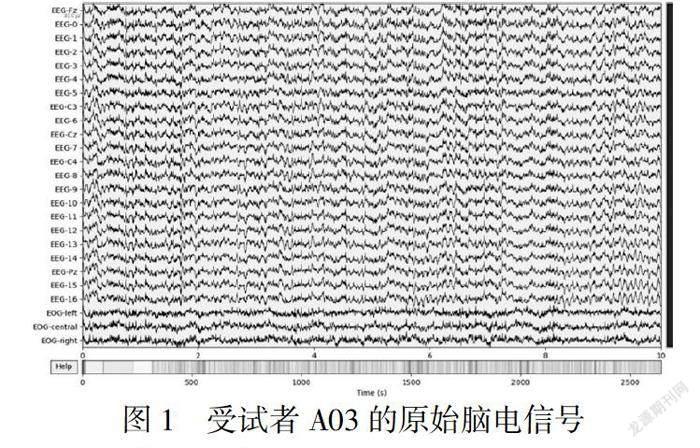
为了更有效地提取脑电信号特征，先对原始脑电数据进行预处理。本文选用Python语言，在集成开发环境PyCharm中进行编程，利用MNE工具箱对脑电信号预处理，受试者A03原始的脑电信号如图1所示。该数据集包含3个眼电伪迹的通道，删除这三个无用通道。与MI有关的频率主要集中在α节律（8～13Hz）和β节律（14～30Hz）[18]，因此对脑电信号进行8-30Hz的带通滤波。滤波后不仅方便选择后续工作所需要的有效频段，而且可以减轻高频干扰与工频噪声[19]。脑电信号中掺杂着各种生理伪迹[20]，调用MNE工具箱中内置的独立成分分析（Independent Component Analysis，ICA）算法进行去噪处理。

2.3 特征提取与降维

2.3.1 特征提取

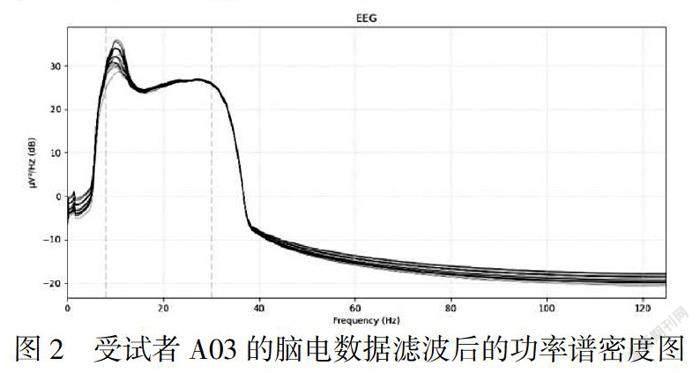
对预处理后的脑电信号使用功率谱密度（Power Spectral Density，PSD）提取反映受试者意图的频域信号特征，受试者A03的脑电数据经带通滤波后的功率谱密度如图2所示。计算对应频率段的曲线下面积作为脑电信号在该频段的能量值。对每名受试者的22个通道分别计算Alpha（8-13Hz），Beta1（14-20Hz），Beta2（21-28Hz）三个频段的脑电信号功率，共提取66维脑电特征。

2.3.2 特征降维

提取到的脑电特征包含许多冗余信息，会影响分类模型的识别准确率，使用主成分分析（Principal Component Analysis，PCA）算法降维。PCA通过矩阵分解将高维特征数据压缩到少量特征上，并且信息量不会损失太多，形成新的含有大量有效信息的低维特征矩阵。

2.4 模参型数

精细调参可以提高分类器的准确率，使用学习曲线和网格搜索的方法确定SVM和LR模型的参数。SVM的核函数设为‘linear，选择L2正则化防止模型过拟合，惩罚项系数C设为0.8，最大迭代次数max_iter为-1。LR模型选用L2正则化，C设为0.78，设置‘lbfgds作为目标损失函数的迭代优化算法。

2.5 概率校准

2.5.1 Platt Scaling

Platt Scaling是一种参数化校准方法，模型校准的过程实际上是在确定最优参数（a，b）。将分类器的预测输出值通过Sigmoid函数进行转换，将分类器的原始预测输出值映射为较为准确的概率值，其范围为（0，1）。假设输入样本为xi，分类器的预测输出值为f（xi），则分类器最终输出概率的计算公式为：

参数（a，b）通过极大似然估计的方法可求得：

其中，pi为校准后的概率，yi为输入样本的真实类别，pi用式（3）表示：

在实际应用中，为了防止分类器过度拟合，经常会使用下式给样本正类y+和负类y-赋值：

其中，N+和N-分别是正负样本的数量。

2.5.2 Isotonic Regression

Isotonic Regression是一种非参数校准的方法，假设分类器预测输出值为yi，输入样本的标签为Yi，则模型定义为：

其中，F为分类器预测输出值yi和样本真实值Yi之间拟合的单调递增的函数，？着i为误差。若给定数据集set（yi，Yi），则F可以通过式（7）求解：

式（6）的一种求解算法是PAV（Pool Adiacent Violators）[21]，通过不断更新违反函数单调性的局部区间，找到最终满足单调性的区间。

3 评估方法与结果分析

3.1 评估方法

模型的评估是非常重要的一步，为了评估概率校准后模型的效果，本文采用了三种指标：布里尔分数（Brier Score），可靠性曲线（Reliability Curve），ROC曲线下面积AUC来评估概率校正后模型的效果。

3.1.1 布里尔分数

布里尔分数是一项衡量概率校准表现的标准指标，其计算方法为样本真实值与概率预测之间的均方误差。具体表达式如下：

其中，N是样本数量，fi是分类器预测输出值，yi是样本的真实标签。式（8）的范围从0到1，衡量概率预测值和真实值的差异，布里尔分数越小，模型的预测精度越高。

3.1.2 可靠性曲线

可靠性曲线，又称为概率校准曲线（Probability Calibration Curve），它是一种可视化的评估方法，可以直观地看出模型在进行二分类任务时，其概率输出与理论最优分类器预测的偏差程度，可以帮助我们了解模型的置信度。如果模型具有很好的置信度，那么可靠性曲线应该接近45度对角线。而如果模型的置信度有问题，可靠性曲线可能会出现明显的偏差。

3.1.3 AUC

ROC（Receiver Operating Characteristic）曲线，又称为感受性曲线，ROC曲线是一种以真阳性率为纵坐标，以假阳性率为横坐标的二维曲线。模型的预测效果可以通过ROC曲线下面积AUC来进行评估，AUC值越大则模型的预测效果越好。通常，AUC值被用来衡量二分类模型的分类效果，其取值范围在0到1之间。当AUC值越接近1时，模型的分类效果越好。

3.2 结果分析

表1展示了9名受试者采集的脑电信号在原始模型和概率校正后模型下的分类准确率。为了叙述方便，下文以‘模型+Platt、‘模型+Isotonic的方式命名校准后的模型。SVM、SVM+Platt、SVM+Isotonic、LR、LR+Platt和LR+Isotonic在9名受试者脑电数据上的平均准确率分别为70.96%、73.74%、72.18%、72.28%、74.78%和73.94%。可以看出经概率校准的分类器的准确率比原始分类器的准确率有所提高，且Platt概率校准方法在该数据集上比Isotonic概率校準方法更有优势。

由于篇幅限制，本文只展示受试者A03的概率校准模型的可靠性曲线图。如图3所示，明显看到经过概率校准的模型SVM+Platt、SVM+Isotonic、LR+Platt和LR+Isotonic都比未校准的模型更靠近对角线，模型效果更好。支持向量机模型的布里尔分数为0.140，经概率校准后SVM+Platt和SVM+Isotonic的布里尔分数分别为0.124，0.126；逻辑回归模型的布里尔分数为0.130，经概率校准后LR+Platt和LR+Isotonic的布里尔分数分别为0.119， 0.120。校准的模型布里尔分数降低，说明模型的概率预测输出与样本真实标签更接近，模型变得更加稳定可靠。

图4展示了应用本文采用的概率校准方法后，SVM+Platt的AUC比原始SVM模型的AUC提高0.03，达到0.93；SVM+Isotonic的AUC略微逊色达到0.92。对于原始LR模型，模型本身效果就比较好，AUC为0.92；概率校准后，LR+Platt的AUC有所上升，达到0.93，而LR+Isotonic的AUC则与LR的AUC持平。

4 討论

本文对第四届BCI竞赛2a脑电数据集进行解码，利用概率校准方法对模型的预测输出进行再学习，模型准确率上升，达到实验预期。概率校准并不是对所有的数据集都起作用，如表1中，受试者A07的脑电数据，经过两种概率校准方法校准后，模型的准确率反而下降；对于受试者A09，经Platt方法校准，模型的准确率升高，经Isotonic方法校准，模型的准确率下降或持平。SVM+Platt、SVM+Isotonic、LR+Platt和LR+Isotonic四种校准模型在9名受试者的脑电数据上进行建模，平均准确率比原始模型分别提高2.78%，1.22%，2.50%，1.66%。通过调研文献资料发现，Platt校准方法在数据量较少时会有更好的效果，因为Isotonic校准方法非常容易过拟合，当有足够多的数据时，Isotonic方法会更有效。

通过绘制交叉验证学习曲线观察6种模型在受试者A03数据集上的表现情况。由于训练数据集和测试数据集分别有144个，数据量偏少，选择将两组数据组合在一起，总共288个数据样本，建立模型后，以每次训练的不同的样本数量为横坐标，训练分数和测试分数为纵坐标来绘制学习曲线，如图5所示。从图上可以看出，支持向量机和逻辑回归模型在训练数据量较小时都存在严重的过拟合现象，随着样本量的增大，模型过拟合的情况会得到缓解；概率校准后，有效地减轻了模型的过拟合情况。两种概率校准后的模型测试准确率均高于原始模型的表现，达到85%以上，且经Platt方法校准的模型表现略胜一筹，说明Platt方法在数据集较少时的表现确实好于Isotonic方法。从图上可以预见，采集更多的脑电数据用于训练，两种方法校准后模型的准确率会进一步提高。

本文的不足之处：第一，只提取脑电信号频域特征，有效信息量过少，接下来工作会从时域、频域、空域三种不同的角度提取脑电信号特征，然后进行特征融合，利用启发式算法选择特征。第二，经典单一分类器的表现效果或许不如多模型融合以及神经网络模型，后续工作会进行验证。

5 结束语

脑机接口技术改变了人们与外界的信息交互方式，在未来许多领域必定会大放异彩，脑电信号的解码至关重要。本文对运动想象脑电信号使用PSD方法提取频域特征，利用PCA技术降低特征维数，选择SVM和LR两种算法建立脑电信号分类预测模型，选用Platt、Isotonic两种概率校准方法对模型有偏的输出结果进行校准，两种方法在本文数据集中多名受试者的脑电数据上均达到不错的效果，且随着数据量的增加，模型过拟合情况得到缓解，分类准确率也能进一步提高。

——————————

参考文献：

〔1〕Kamhi S， Zhang S， Ait Amou M， et al. Multi-Classification of Motor Imagery EEG Signals Using Bayesian Optimization-Based Average Ensemble Approach[J]. Applied Sciences， 2022， 12（12）： 5807.

〔2〕许冬萍，陈峰.基于改进小波变换和模糊熵的脑电信息研究[J].计算机仿真，2019，36（10）：227-232.

〔3〕Yang Y J， Jeon E J， Kim J S， et al. Characterization of kinesthetic motor imagery compared with visual motor imageries[J]. Scientific Reports， 2021， 11（01）： 1-11.

〔4〕田贵鑫，陈俊杰，丁鹏，等.脑机接口中运动想象的执行与能力的评估和提高方法[J].生物医学工程学杂志，2021，38（03）：434-446.

〔5〕刘拓， 叶阳阳，王坤，等.运动想象脑电信号分类算法的研究进展[J].生物医学工程学杂志，2021， 38（05）：995-1002.

〔6〕Li C， Chen M， Zhang L. A Domain Adaptation-Based Method for Classification of Motor Imagery EEG[J]. Mathematics， 2022， 10（09）： 1588.

〔7〕鲁杰，杨晓栋，彭靖宇，等.基于LSTM的运动想象脑电信号分类方法[J].电子设计工程，2021，29（04）：88-92.

〔8〕Shi M， Wang C， Li X Z， et al. EEG signal classification based on SVM with improved squirrel search algorithm[J]. Biomedical Engineering/Biomedizinische  Technik， 2021， 66（02）： 137-152.

〔9〕Miao M， Zeng H， Wang A， et al. Discriminative spatial-frequency-temporal feature extraction and classification of motor imagery EEG： An sparse regression and Weighted Na？觙ve Bayesian Classifier-based approach[J]. Journal of neuroscience methods， 2017， 278： 13-24.

〔10〕Niculescu-Mizil A， Caruana R. Predicting good probabilities with supervised learning[C]//Proceedings of the 22nd international conference on Machine learning. 2005： 625-632.

〔11〕Zadrozny B， Elkan C. Transforming classifier scores into accurate multiclass probability estimates[C]//Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining. 2002： 694-699.

〔12〕Zhong W， Kwok J T. Accurate probability calibration for multiple classifiers[C]//Twenty-Third International Joint Conference on Artificial Intelligence. 2013.

〔13〕范双龙，赵志强，余红梅，等.基于概率校准的弥漫性大B细胞淋巴瘤患者死亡风险预测[J].中国卫生统计，2021，38（05）：670-674.

〔14〕肖瑶，谢贵才，朱兵.浅谈分类问题中的概率校准[J].中国统计，2018，66（05）：35-37.

〔15〕Platt J. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods[J]. Advances in large margin classifiers， 1999， 10（03）： 61-74.

〔16〕Qin J， Garcia T P， Ma Y， et al. Combining isotonic regression and EM algorithm to predict genetic risk under monotonicity constraint[J]. The annals of applied statistics， 2014， 8（02）： 1182.

〔17〕Naeem M， Brunner C， Leeb R， et al. Seperability of four-class motor imagery data using independent components analysis[J]. Journal of neural engineering， 2006， 3（03）： 208-216.

〔18〕Tang Z， Li C， Sun S. Single-trial EEG classification of motor imagery using deep convolutional neural networks[J]. Optik， 2017， 130： 11-18.

〔19〕Daud S S， Sudirman R. Butterworth bandpass and stationary wavelet transform filter comparison for electroencephalography signal[C]//2015 6th international conference on intelligent systems， modelling and simulation. IEEE， 2015： 123-126.

〔20〕吴全玉，张文强，潘玲佼，等.一种结合自适应噪声完备经验模态分解和盲反卷积去除脑电中眼电伪迹的新方法[J].数据采集与处理，2020，35（04）：720-729.

〔21〕Ayer M， Brunk H D， Ewing G M， et al. An empirical distribution function for sampling with incomplete information[J]. The annals of mathematical statistics， 1955： 641-647.

收稿日期：2023-02-11

通讯作者：吴全玉（1977-），男，汉族，安徽砀山人，副教授，硕士研究生导师。研究方向：嵌入式康复系统开发、医学信号处理和血流动力学仿真。

基金項目：国家自然科学基金青年项目（62001196）；江苏省重点研发计划（SBE2020648）；常州市社会发展项目（CE20225045）