基于多传感器零速修正的消防员定位算法研究

牛仁杰,程 玉,陈 帅,陈 曦,廖泽俣,袁思思

（南京理工大学自动化学院,南京 210094）

0 引言

消防员在大跨度大空间的灾害现场因迷失方向而伤亡的案例较多,例如: 2012年2月1日,苏州工业园区厂房发生火灾,1 名消防员在内攻侦察时因导向绳被倒塌的货物埋住而在复杂的环境中迷失方向英勇牺牲;2013年10月11日,北京石景山区苹果园南路喜隆多商场发生火灾,2 名消防员进入火场侦查,因火势迅速蔓延,建筑突然坍塌,导致2 人在火场迷失方向壮烈牺牲。因此在消防和灾难救援中,保障消防员自身安全,对救援人员进行定位是有必要的[1]。

以往的行人定位都是在开阔的室外场景,全球导航卫星系统（Global Navigation Satellite System,GNSS）为救援人员提供实时、精准、可靠的定位服务。然而,卫星定位也不是无所不能的,在高楼、隧道等环境中卫星信号经常受到干扰,灾害过后的坍塌环境卫星信号遮挡更严重,基本上无法依靠卫星[2]。当GNSS 不能正常利用时,捷联惯导（Strapdown Inertial Navigation System,SINS）独特的优点就显现出来了,通过连续地采样可以实时获得救援人员的位置信息。

目前,郑佳瑶等[3]对于行人导航中的航向角误差采用有步态约束的序列检测算法,修正了航向角的漂移,抑制了发散,其定位误差占总路程的0.7%,有效改善了导航精度。Johann 等[4]利用建筑物的方向将人在建筑物内的行走分为4 个或8 个主要方向,然后对航向进行约束。尹航[5]提出了利用室内地图修正航向的方法,采用拓扑化规则提取门、房间、走廊等在空间中具有固定关系的特征并存储在数据库中,在消防员行走时利用地图匹配算法修正其位置,由于该算法以原始的空间结构图作为室内地图,所以消防救灾中难以实现。

我国在消防救援环境的个人定位研究相对较少,本文在零速检测的基础上设计了一种基于多传感器零速修正的消防员定位算法。该方法以零速修正为基础,将惯性传感器、磁强计、高度计固连在鞋上测量脚部的运动信息,利用Kalman 滤波算法对导航误差进行零速修正,可实现无信标环境下消防员的自主定位,最后对算法精度进行了验证。

1 消防员定位算法构架

基于多传感器辅助的消防员定位零速修正算法架构设计如图1所示,由惯性器件输出、磁强计输出、高度计输出、捷联惯导解算单元、步态检测单元、Kalman 滤波组成。

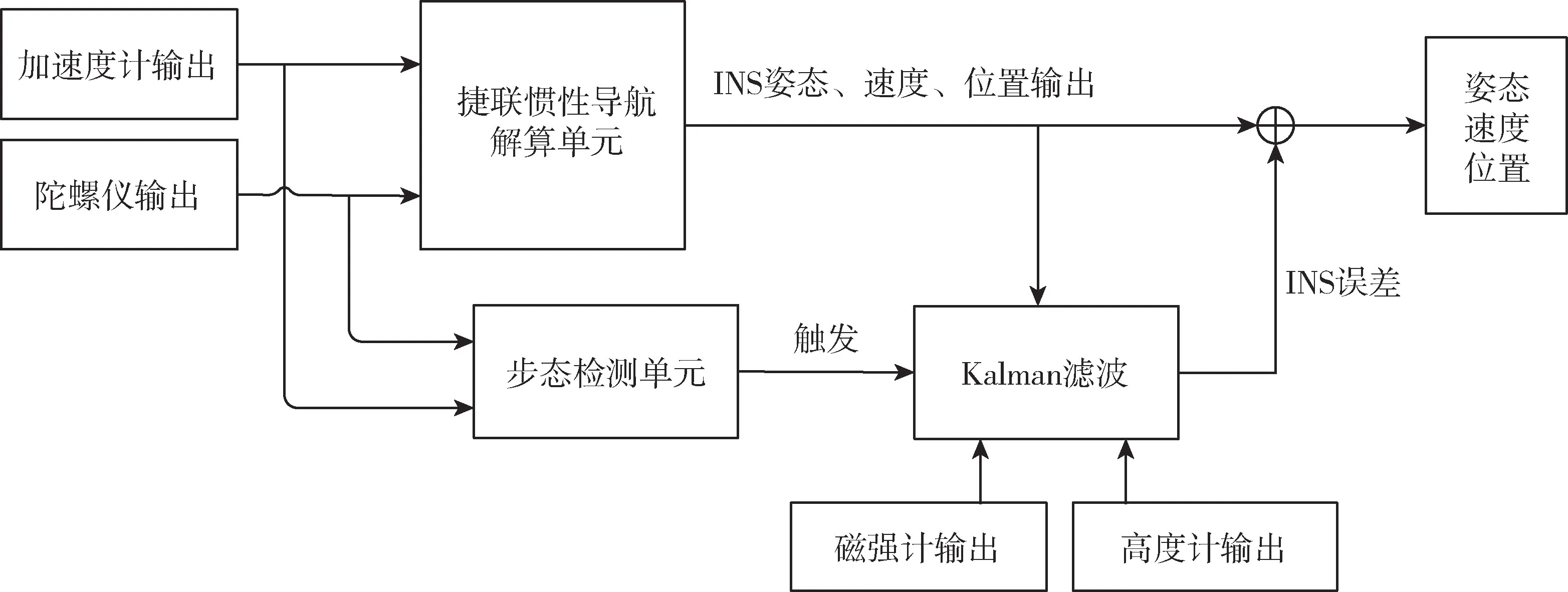
图1 基于多传感器辅助的消防员定位零速修正算法结构图Fig.1 Structure diagram of zero-velocity update algorithm for firefighter positioning based on multiple sensors assistance

在行走过程中,消防员脚跟和脚尖完全着地时,惯性器件输出几乎为零,根据这一特点触发零速检测,结合高度计和磁强计输出的高度信息和航向信息,设计Kalman 滤波器来对速度误差、航向误差、高度误差进行最优估计。

本文的消防员定位算法以捷联惯导为核心传感器,因此在惯导解算之前首先要进行初始对准,利用加速度计静止时三个方向的加速度计输出即可完成水平对准,计算公式为[6]

式（1）中,θ0和γ0为俯仰角和横滚角估算值,g0为重力加速度,fbibx、fbiby、f bibz为x轴向、y轴向、z轴向的加速度计输出。航向角φ0由校正过的磁强计单独给出。

2 零速区间检测算法

图2所示为简化版的步伐周期示意图。步伐周期从右脚迈出阶段开始,然后进入右脚落地阶段,接着进入左脚迈出阶段,最后进入左脚落地阶段。在左脚和右脚落地的过程中,只有脚跟和脚尖完全着地阶段是本文要检测的零速时间段。

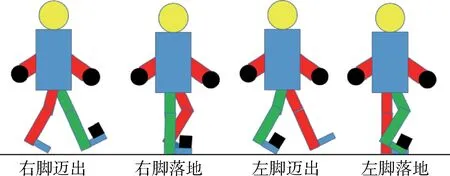
图2 行人步伐周期示意图Fig.2 Schematic diagram of the pedestrian stride cycle

在零速修正方面,步态检测是至关重要的一个环节。为了保证检测的准确性,需要同时利用加速度计和陀螺仪输出的数据,采用两个条件（T1和T2）综合判断运动状态,以状态“0” 表示运动,状态“1” 表示静止。

条件1（T1）: 加速度计输出合成幅值,处于给定的上下阈值之间则人体静止。

定义加速度计的输出合成幅值为[7]

式（2）中,abkx、abky、abkz分别为加速度计输出的加速度。

定义给定的阈值为amin=9m/s2和amax=10.9m/s2,并有

条件2（T2）: 陀螺仪输出合成幅值,低于给定阈值则人体静止。

定义陀螺仪的输出合成幅值为[7]

式（4） 中,ωbkx、ωbky、ωbkz分别为陀螺仪输出的角速度。

给定的阈值为ωmax=10（°） /s,并有

两个条件之间采用“与” 逻辑,即只有当两个条件的判断结果都为“1” 时才认为目标处于静止状态。

从实际步行实验采集到的数据来看,加速度计和陀螺仪的输出合成幅值和曲线并不光滑,如图3所示。这是因为安置在脚上的微惯性器件不仅仅随着脚步做前进且周期性的交替运动,同时它还存在高频次的左右向和上下向的生理抖动。对这样的加速度计和陀螺仪信号进行步态检测很容易被包含在其中的杂波信息和局部极值点影响造成误判,解决方法是先对加速度计和陀螺仪进行滤波,再对平滑后的曲线辨识。本文选用Savitzky-Golay 滤波器对数据进行平滑处理,图4为用原始数据和滤波后的数据分别进行逻辑判断的对比,可以看出使用Savitzky-Golay 滤波器滤波后的数据拥有更好的判断效果。

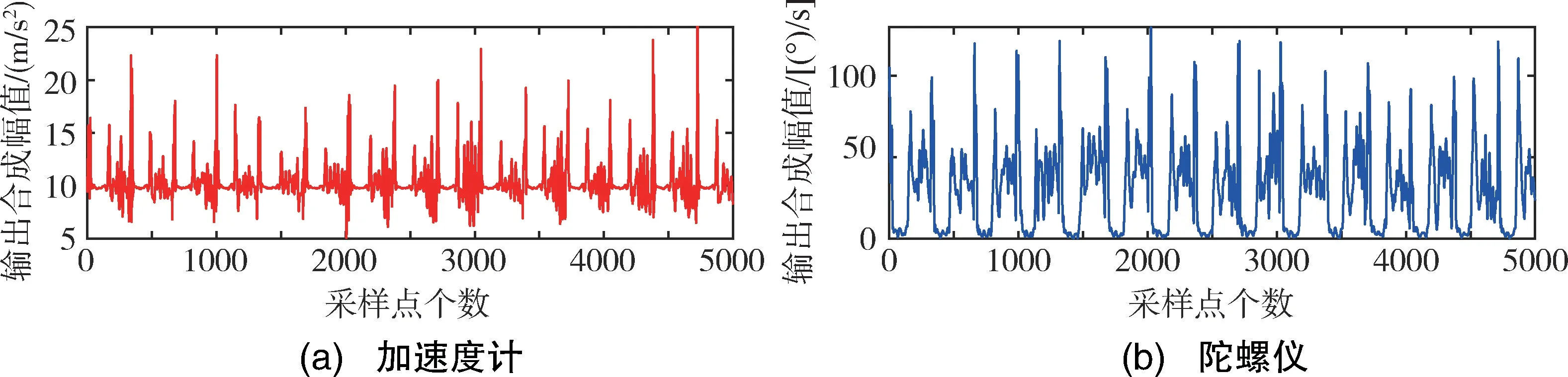
图3 加速度计和陀螺仪的输出合成幅值Fig.3 Output synthesis amplitude of accelerometer and gyroscope

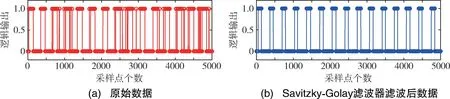
图4 零速区间检测结果Fig.4 Test results of zero-velocity range

对陀螺仪输出合成幅值滤波时,Savitzky-Golay滤波器的滑动窗口宽度为71,多项式阶次为3 阶,滤波前后对比如图5所示。对加速度计输出合成幅值滤波时,Savitzky-Golay 滤波器的滑动窗口宽度为85,多项式阶次为3 阶,滤波前后对比如图6所示。由图5、图6可知,滤波之后传感器原始数据的高频噪声明显减少,为步态检测的准确度奠定基础。

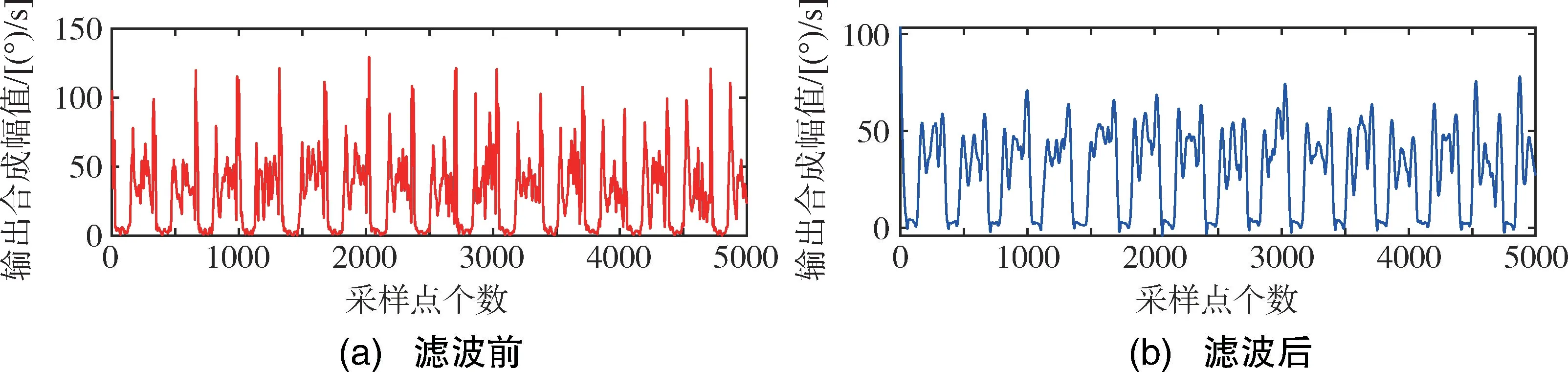
图5 滤波前后陀螺仪输出合成幅值对比Fig.5 Comparison of gyroscope output synthesis amplitude before and after filtering

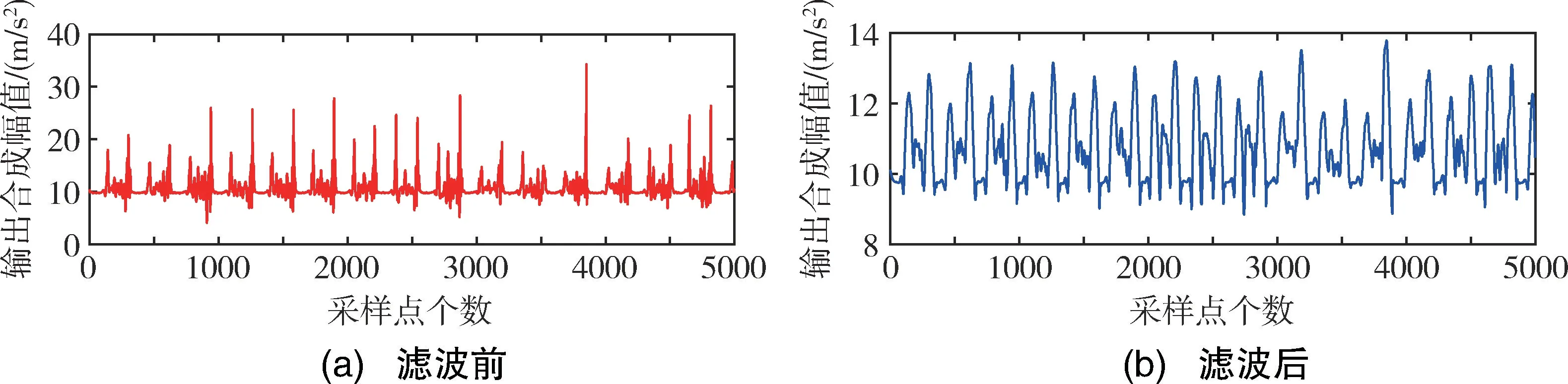
图6 滤波前后加速度计输出合成幅值对比Fig.6 Comparison of accelerometer output synthesis amplitude before and after filtering

3 Kalman 滤波器

对系统状态量进行分析是设计Kalman 滤波器的前提,零速修正的Kalman 滤波状态方程依据惯性导航误差方程推导而来,惯性导航误差方程可以细分为姿态误差方程、速度误差方程与位置误差方程,在导航坐标系（n）即地理系下可表示为[8]

式（6）中,、、分别为失准角误差、速度误差、位置误差对时间的导数,和δωnin为导航系相对惯性系的角速度及其误差在导航系下的投影,ωnie和δωnie为地心地固坐标系相对惯性系的角速度及其误差在导航系下的投影,f n为比力在导航系下的投影,δf b、δωb、δg分别为载体系下加速度计量测误差、陀螺仪量测误差以及扰动重力误差,为导航系相对地球系的角速度在导航系下的投影。

在零速修正时由于载体相对地面静止,故可将其简化为

系统的状态方程为

式（8）中,X（t）为由SINS 误差变量构成的15 维状态向量,F（t）和G（t）为关于时间参数t的确定性时变矩阵,W（t）为零均值Gauss 白噪声向量。

系统的状态向量设计为

式（9）中,φe、φn、φu分别为捷联式惯性导航系统在东北天上的姿态角误差,δve、δvn、δvu分别为捷联式惯性导航系统在东北天上的速度误差,δL、δλ、δh分别为捷联式惯性导航系统纬度、经度、高度的位置误差,δωbx、δωby、δωbz分别为陀螺仪在x、y、z三个轴向上的随机常值误差,δf bx、δfby、δfbz分别为加速度计在x、y、z三个轴向上的一阶Markov 偏移误差[9]。零速修正的15 维状态模型为

本文将纯惯性解算的航向角与磁强计航向的差值、纯惯性解算的速度vins与零速的差值、纯惯性解算的高度与高度计的差值作为系统量测向量,系统量测方程为

式（11）中,φins为捷联惯导输出的航向角信息,φc为磁强计输出的航向角信息,vinse、vinsn、vinsu为捷联惯导输出的地理系下载体在东北天上的速度信息,hins为捷联惯导输出的高度信息,ha为高度计输出的高度信息,H（t）为量测矩阵,V（t）为量测噪声。

定义

则式（11）中,

通过时间更新可以得到估计协方差为

式（14）中,Φk,k-1为k-1 时刻到k时刻的系统一步转移矩阵;Γk-1为系统噪声矩阵,表征由k-1时刻到k时刻的各个系统噪声分别影响k时刻各个状态的程度;Qk-1为系统噪声的方差矩阵。

在量测更新过程中,根据误差协方差Pk|k-1算出Kalman 滤波增益Kk,然后再结合当前时刻的测量值Zk进行状态估计更新。

k时刻的Kalman 滤波增益为

式（15）中,Rk为量测噪声的方差矩阵。

则状态估计为

估计误差协方差更新为

4 实验与分析

为了验证本文所述基于多传感器零速修正的消防员定位算法的可靠性和有效性,共设计了两组半物理仿真实验。

如图7所示,实验1 将惯导、磁强计、高度计固联在测试者脚面,以NovAtel-KVH1750 作为基准,通过usb 接口和计算机相连接,通过数据采集上位机采样数据,后期用Matlab 对数据进行仿真处理,设备性能指标如表1所示。本算法的实验场景选为南京理工大学标准400m 操场,测试者穿戴好装置,在实验场地按照逆时针行走一周,黑色实心圆为初始点,向北出发,行走路径是一个封闭环形。

图7 算法验证设备和行动轨迹Fig.7 Diagram of algorithm verification devices and action trajectory

表1 实验设备性能指标Table 1 Performance indexes of experiment devices

实验中,给定陀螺仪的输出合成幅值阈值为ωmax=10（°） /s,加速度计的输出合成幅值阈值为amin=9m/s2和amax=10.9m/s2,行走时长约800s,初始对准时长约25s。由图8可知,传统ZUPT 算法航向角由于其不可观测的特性容易发散,水平误差为19.74m,约为总路程的4.93%,加入磁强计修正后水平误差降至2.58m,约为总路程的0.65%,误差比小于1%D。由图9可知,加入高度计约束之后,高度误差减小为原来的16.33%,从而验证了本文算法的有效性和可行性。

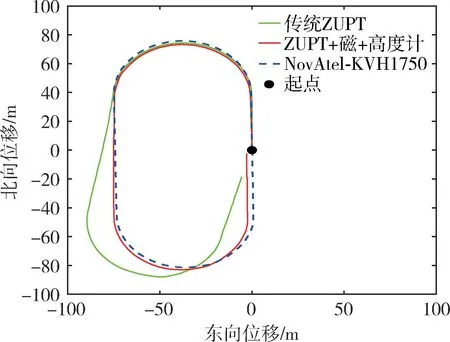
图8 传统零速修正、本文算法和基准位置对比Fig.8 Comparison of traditional zero-velocity update,proposed algorithm and benchmark position

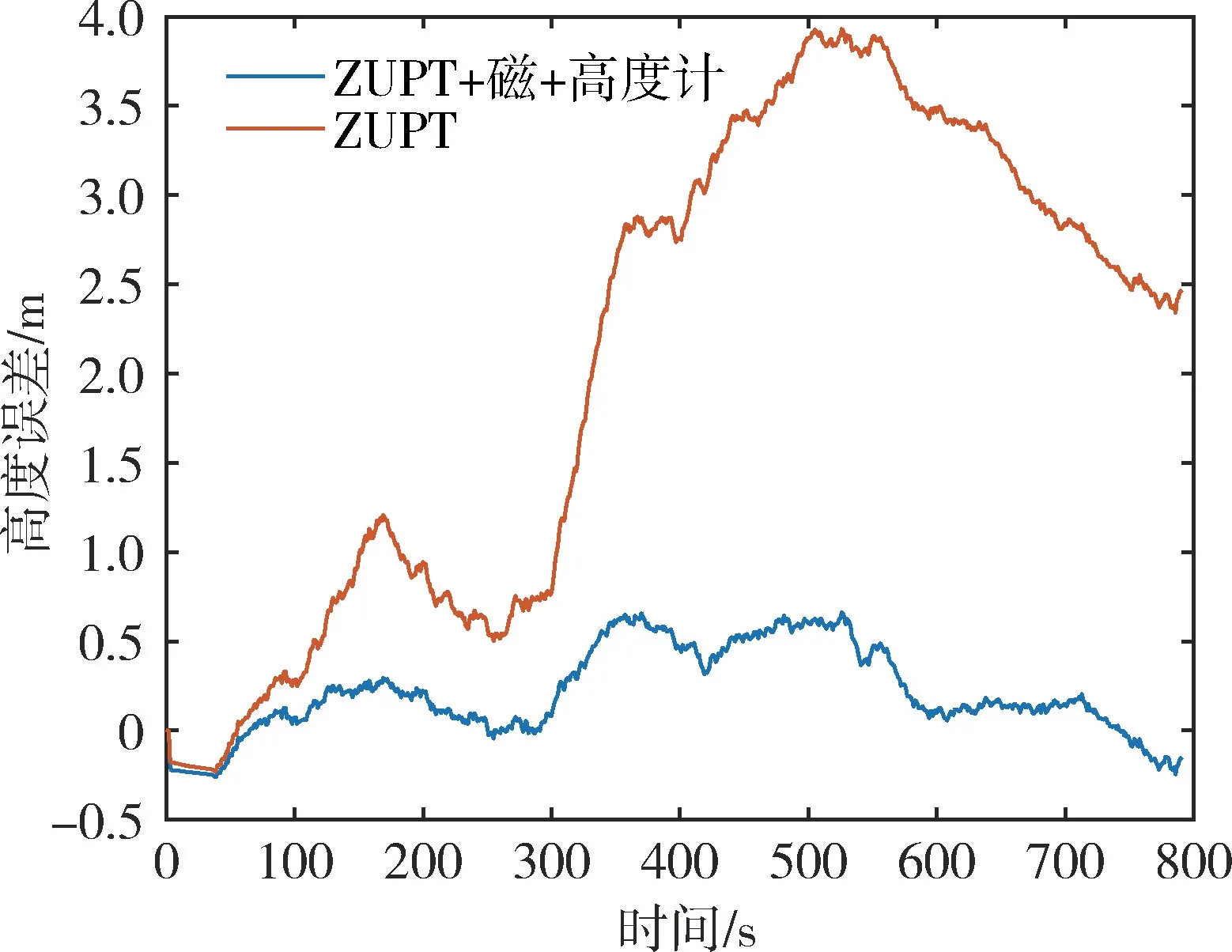
图9 高度误差对比Fig.9 Comparison of height error

由图10可知,横滚角和俯仰角变化很小,航向角由于磁强计的修正变化趋势正常,经历了0°～180°（-180°）～0°的变化,充分验证了磁强计修正航向的可行性。图11为测量的加速度和角速度数据（为方便查看,截取前100s 数据）。

图10 行人实时姿态Fig.10 Diagram of pedestrian real-time attitude

图11 加速度和角速度测量结果Fig.11 Measurement results of acceleration and angular velocity

实验2 在室内环境下按照“8” 轨迹行走,实验行走路径大约75m,如图12所示。黑色实心圆为初始点向上出发,经过一个“8” 字形从左侧绕回来,“∗” 为终点结束实验,行走路径是一个封闭的双环形,场地距离用卷尺进行测量。绿色曲线为传统零速修正算法轨迹,由于没有磁强计约束,因此在结尾处航向角有偏移,轨迹起点与终点未能重叠;红色曲线为本文算法轨迹,由于加上了磁强计的约束,轨迹起点与终点重叠。

图12 室内行人轨迹对比Fig.12 Comparison of indoor pedestrian trajectories

由图13可知,横滚角和俯仰角变化很小,航向角由于磁强计的修正变化趋势正常,经历了0°～90°～0°～-90°～180°（-180°）～90°～180°（-180°）～-90°的变化,验证了消防员在任意方向行走时航向角依然正确。

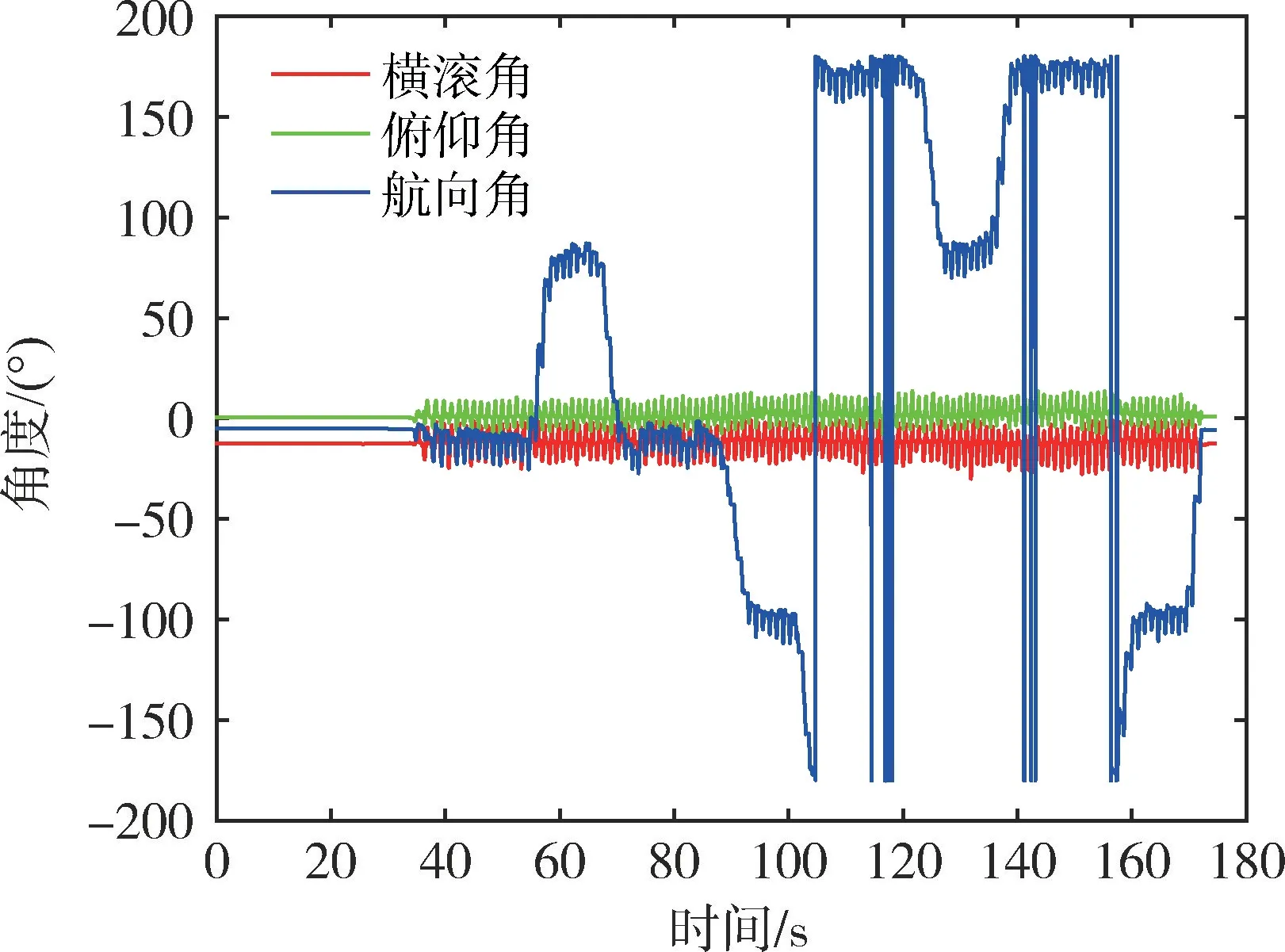
图13 室内行人实时姿态Fig.13 Diagram of indoor pedestrian real-time attitude

5 结论

消防员在大跨度大空间的灾害现场因迷失方向而伤亡的案例较多。因此,本文针对消防救援时出现卫星拒止导致定位精度差的问题,在传统零速修正的基础上增添磁强计、高度计进行辅助定位,解决了传统算法航向角和高度随时间发散的问题,可实现无信标环境下消防员自主定位。通过操场和室内两种环境下的半实物仿真实验对算法有效性进行验证,结果表明: 本文的多传感器零速修正定位算法在复杂环境中精度效果好,鲁棒性高,误差比不超过1%D。