无人机视觉导航相对位置解算及二义性优化方法
2023-05-19齐艳霞李岳伦梅志强付英华
齐艳霞,庄 羽,李岳伦,梅志强,付英华,李 冲
(1.河南九域博慧方舟咨询发展有限公司,郑州 450052;2.北京理工大学自动化学院,北京 100081)
0 引言
随着无人系统的应用与研究不断扩展与深入,以无人机与无人车为代表的无人系统广泛地被应用于生产生活中的诸多领域,例如工厂自动化、建筑、采矿、电力、农业以及军事装备等。近年来,人们开始使用异构多智能体无人系统以完成更加复杂的任务,这也使得无人系统异构智能体间的相对导航技术受到了国内外学者的广泛关注[1-3]。
同时,根据应用需求的增加和细致化,需要在室内、地下、隧道、对抗干扰等复杂、随机、多变的环境下进行作业[4],而常见的主动式相对导航方法,如全球卫星导航系统(Global Navigation Satellite System,GNSS)、超宽带(Ultra-wideband,UWB)、激光雷达(LiDAR)等[5-8],或因为信号被遮挡、屏蔽,或因为传感器尺寸大、能耗高,或因为基站部署的硬件成本居高不下,在上述复杂环境下很难得到应用,相对导航精度与效果无法得到保障。而一些非主动式相对导航方法,如基于视觉[9-10]和惯性导航系统(Inertial Navigation System,INS)等[11]非主动式传感技术的相对位置估计方法,与主动式传感器相比,具有抗干扰能力强,传感器尺寸小、能耗低、质量小等优点。因此,在卫星拒止条件下,无人系统内部异构智能体间可采用基于视觉的相对导航方法,并利用智能体间可视觉识别的合作标识实现诸如无人机与无人车间的协同导航与相对位置解算[12-15]。
当前,基于合作标识的技术方案是所有视觉引导的无人机相对位置估计技术中最为成熟、应用最为广泛的。主流方案采用二进制编码表示物即ArUco 作为合作标识物,主要依靠二维码提供的角点信息来实现[16-18],但是二维码角点提取对相机成像质量要求较高,因此复杂环境下相对位置解算的鲁棒性较差。而相对于传统的二进制编码标识物,自行设计的地标可以极大地减少解算位置所需参数,减小计算量,提高位置解算算法实时性。因此,圆形、矩形、H 形、T 形及不同形状组合的自主设计合作标识应运而生[19-21]。上述合作标识的识别方法主要可以采用基于角点的检测方法和基于形状特征的检测方法: 利用提取到的特征点,基于角点的检测方法能够快速实现相对位置解算,但对成像质量要求较高;基于形状特征的检测方法易于检测和识别合作标识,但难以获取高精度相对位置信息[22]。
面向复杂环境下无人机与无人车之间的相对位置估计难题,本文开展了无人机视觉自主相对导航方法研究,提出了基于椭圆合作标识边缘检测和位置解二义性优化方法。首先,设计了具有同心圆特征的合作标识,以提升不同距离情况下合作标识检测的鲁棒性;其次,通过椭圆模型将相对位置解算问题转换为高次方程求解问题,实现像素坐标系下椭圆方程拟合;然后,提出了基于特征点的相对位置初始化方法和基于运动约束的相对位置跟踪方法,以解决纯视觉相对位置解算过程中存在的二义性问题;最后,开展了卫星拒止条件下的实验,验证了所提方法的有效性,实现了复杂场景下厘米级或分米级高精度相对位置解算。
1 基于合作标识的边缘检测及椭圆方程拟合
相对导航过程中,无人机与无人车组成的空地无人系统采用具有同心圆特征的图案作为合作标识,该合作标识与无人车固连,合作标识半径和相机内参已知,能够提供相对位置解算所需的先验信息。为了实现高精度的相对位置解算,有必要在像素坐标系下检测合作标识的椭圆边缘并拟合椭圆方程。
如图1所示,建立圆形合作标识在像素坐标系(u-v)下所呈现的椭圆方程参数(a~f)到空间圆(即蓝色圆)在相机光心坐标系(x-y-z)下相对位置的映射模型。坐标系(xe-ye-ze)为空间圆圆心坐标系,且ze轴为空间圆在相机光心坐标系下的方向向量。考虑到无人机有限的机载算力和椭圆拟合高精度的需要,本文采用基于边缘检测的椭圆方程拟合算法。

图1 空间圆在像素坐标系下的成像示意图Fig.1 Imaging diagram of spatial circle in pixel coordinate system
如图2所示,算法分四个步骤: 在步骤1 中使用改进的Canny 边缘检测算法,沿图像45°和135°方向进行边缘检测,并将离散的边缘连接成边缘簇,从而根据边缘簇的检测梯度将边缘分为两类;步骤2 根据边缘簇的凹凸性将边缘簇再分为两类,此时步骤2 输出的边缘簇共可分为四类;步骤3 标记所有边缘簇的左右边缘点,并根据左右边缘点的距离将可能连接的边缘簇封装到同一个边缘簇集合内,当边缘簇集合满足椭圆的定义,即边缘簇集合中包含四类边缘簇且按一定的顺序首尾连接,则该边缘簇集合即椭圆边缘簇集合;步骤4 主要对内外同心圆进行识别,并在仅识别出一个圆的情况下,通过对历史帧内外圆参数的约束,恢复另一个圆对应的椭圆方程,并借助最小化当前帧与历史帧椭圆方程参数的误差,实现内外圆的鲁棒识别。
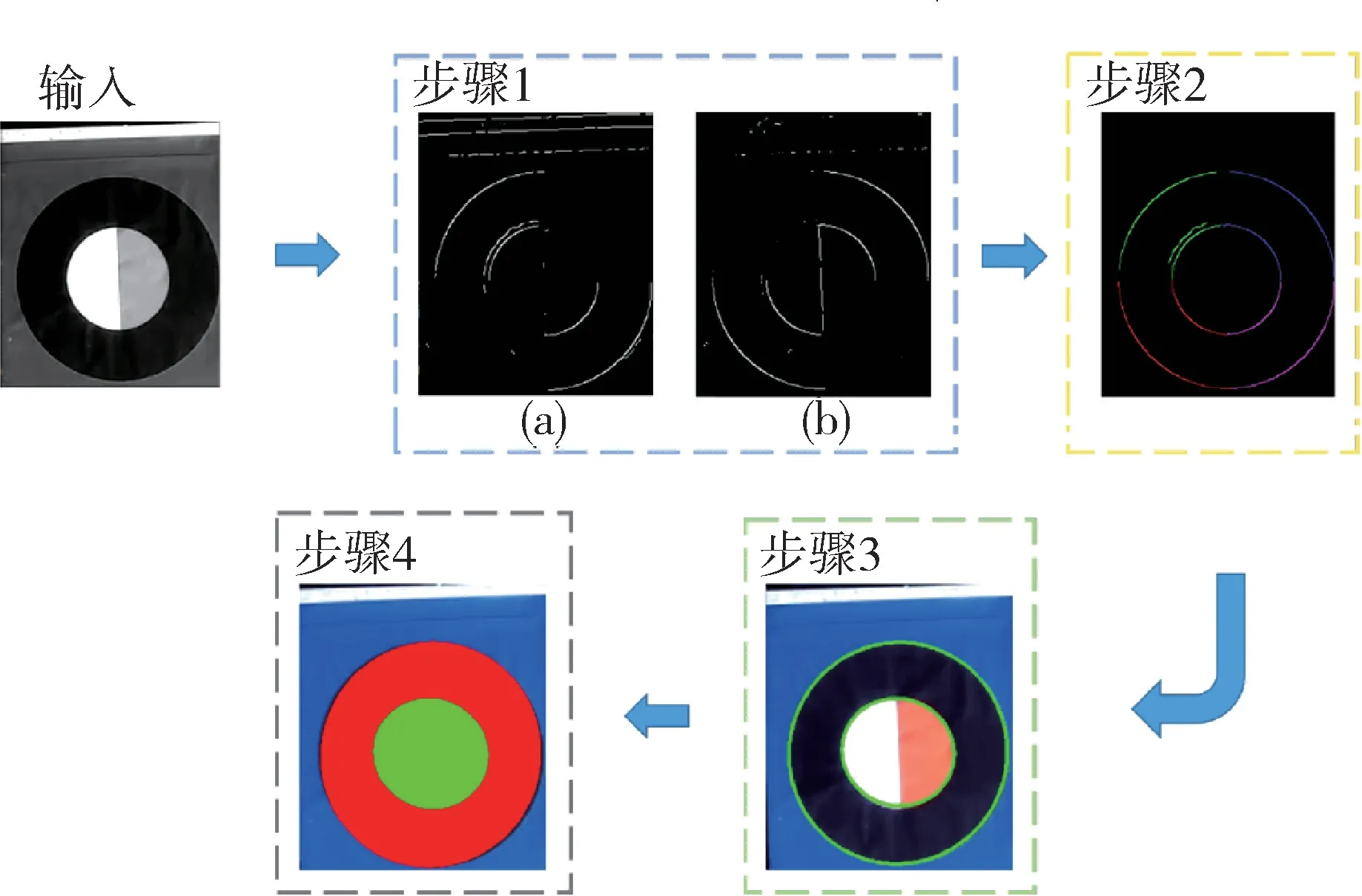
图2 基于边缘检测的椭圆拟合算法Fig.2 Diagram of ellipse fitting algorithm based on edge detection
在获取椭圆边缘簇集合后,便可以开始拟合椭圆方程参数,且椭圆方程定义为
进而,将椭圆方程拟合问题建模为最小二乘问题,令W=[abcdef]T、X=[x2xyy2xy1]T,则优化目标为
理论上,采用最小二乘方法,利用N个椭圆方程上的离散点(x,y),基于最速下降优化方法,即可求得椭圆参数实现椭圆拟合。但该方法只考虑了离散点之间的相关性,椭圆方程拟合精度较低,鲁棒性较差。为了提升了椭圆拟合的实时性、鲁棒性和精度,本文提出了融入边缘信息的椭圆拟合方法。如图3所示,首先基于获取的椭圆边缘簇集合解算出椭圆中心坐标;然后,根据椭圆方程的性质即椭圆上平行弦的中点是共线的,分别从椭圆边缘簇集合四个分类中的三个两两构建平行弦,并连接中点成中点线;最后,对中点线之间的交点取平均值,得到椭圆方程的中心坐标(xc,yc)。

图3 基于椭圆边缘簇集合的椭圆中心坐标解算Fig.3 Diagram of ellipse center coordinate solution based on ellipse edge cluster set
根据椭圆性质可知,椭圆中心与椭圆方程参数的关系为
在式(2) 基础上加入椭圆中心约束,即(xc-)2+(yc-)2<ρ,则有
进而,利用提取且分类的连续椭圆边缘簇信息,在最小二乘方法的基础上施加了对椭圆方程中心的约束,实现精度更高、鲁棒性更好的椭圆方程拟合。
2 相对位置解的二义性及其优化方法
空间圆在相机光心坐标系下相对位置和方向向量会存在两个解,即存在二义性的问题。如图4所示,在同一圆锥面内,可能对应一个像素坐标系下两个空间圆,且两个空间圆相对某一平面相互对称。理论上,像素坐标系下所呈椭圆方程具有5 个变量,而空间中的相对位置和方向向量具有6 个自由度,因此在不引入其他约束的情况下,必然会产生二义解。
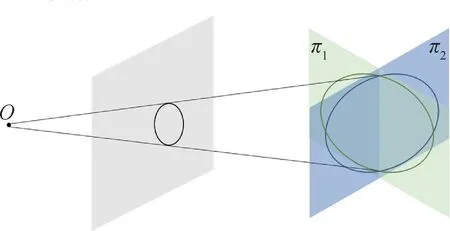
图4 二义性产生的原理示意图Fig.4 Schematic diagram of ambiguity principle
对于无人机与无人车组成的空地无人系统来说,相对导航位置解算时二义解问题分析如下:1)初始化阶段,由于没有相对位置历史信息,或者较长时间内相机视野中未出现合作标识,无法为当前相对位置的解算提供运动约束;2)跟踪阶段,存在有效的相对位置历史信息,能够为当前相对位置的解算提供运动约束;3)过零阶段,即当相对运动使得空间圆在像素坐标系下呈正圆时,空间圆方向向量的延长线会经过相机光心,此时利用相对位置历史信息难以为当前相对位置的解算提供运动约束。
为了解决二义性问题,本章分别针对上述不同阶段,给出了相应的解决方法。
2.1 基于特征点的相对位置初始化配准方法
基于特征点的相对位置初始化配准方法主要通过三帧匹配特征点对应的基础矩阵求解相对位置,进而提供初始化运动约束,实现对二义性问题的求解。理论上,利用基础矩阵求解相对位置是多视图几何中经典的2D-2D 极几何问题,且该过程只与相机的内参和帧间相对位置有关。从几何代数的角度,分析基本矩阵内在的射影几何。设三维空间点P=[XYZ]T,P在两帧下的像素点坐标p1和p2满足
式(5)中,K为内参矩阵,s1和s2为对应深度,R和t分别为帧间的旋转矩阵和位移矩阵。将式(5)写成齐次坐标的形式,可以得到
假设,x1和x2分别为p1和p2的归一化坐标,即
由式(6)和式(7)可得
式(8) 两侧同时与t做外积,并同时左乘xT2,可得
式(9) 中,t∧为t的反对称矩阵。进而,不难得到
式(10)中,E=t∧R。
代入p1和p2后,得到
或
式(12)中,F=K-TEK-1为基础矩阵。
在获得足够的匹配点对后,通过帧间若干个匹配的特征点,可以求解出帧间相对位置对应的基本矩阵F,进而采用八点法求得帧间旋转矩阵R和位移矩阵t。
在基于特征点进行相对位置初始化配准过程中,利用对极几何的约束,设计基本矩阵的评价准则。
解算出的基本矩阵F质量越好,则通过匹配获得的p2与由F得到的极线l2的距离d=越小。因此,基本矩阵F的评价标准为
式(14)中,n为两帧中匹配的特征点对数;当j=1 时k=2,当j=2 时k=1;{αj,βj,γj} 为由基本矩阵F在像平面lj生成的极线方程参数;(ukj,vkj)为在像平面lk上的第j对特征点;ρ(·)为方差归一化。
2.2 基于连续帧运动约束的相对位置跟踪方法
当合作标识能够稳定地出现在相机视野中时,能够有效获得相机在空间圆圆心坐标系下的初始相对位置和方向向量。由于方向向量会随着无人机运动而朝着相反的方向旋转,因此可以通过相机运动感知以及初始相对位置和方向向量的约束有效解决二义解的问题。
如图5所示,在跟踪阶段存在有效的相对位置历史信息,能够为当前相对位置的解算提供运动约束。已知前一帧相对位置和方向向量分别为Xn-1和Vn-1,为求得当前帧相对位置和方向向量Xn和Vn,构造方向向量约束条件

图5 相对运动约束下的二义性问题示意图Fig.5 Schematic diagram of ambiguity problem under relative motion constraints
式(15)中,V∗n为符合约束条件的正确方向向量,X∗n为对应的相对位置解。
在过零阶段,即当相对运动使得空间圆在像素坐标系下呈正圆时,空间圆方向向量的延长线会经过相机光心,此时利用上述相对位置历史信息难以为当前相对位置的解算提供运动约束,不能保证获得唯一解。
为此,通过利用历史多帧提供的相机在空间圆圆心坐标系下的历史旋转向量信息,为当前相对位置的解算提供运动约束,从而实现鲁棒的二义解筛选。假设,历史帧的位置和方向向量为XN和VN,且N∈n-1,n-2,…;当前帧的相对位置和方向向量的二义解为{Xn1,Vn1} 和{Xn2,Vn2}。令帧间平均旋转轴为
式(16)中,vi(i=1,2,…,n-1)为历史帧方向向量的旋转轴。
此时,当前帧与上一帧的帧间旋转轴v∗应满足
通过式(17)约束进行鲁棒的二义解筛选后,即可得到二义解的真实解v∗n以及对应的当前帧相机在空间圆圆心坐标系下的位置和方向向量{,}。
3 实验验证与结果分析
为了验证所提出的相对位置解算方法的正确性和有效性,本文开展了卫星拒止条件下视觉相对导航实验,以验证相对位置和相对姿态解算的精度、鲁棒性和实时性。实验过程中,在室内自然光照条件下采集了相机与合作标识处于白色背景板上的相对运动视频,并建立了基于视觉信息的相对导航数据集,数据集中包含了平行、垂直以及合作标识方向向量经过相机等多种运动模式。
采用本文所提方法和基于二维码ArUco 的相对位置解算方法,得到如图6所示的相对位置解算轨迹和如图7所示的相对位置解算结果。因为基于二维码相对位置估计算法在室内场景以及相对距离较近时拥有较高的解算精度,因此在此次实验中,使用ArUco 位置解算算法获得的相对运动位置轨迹作为参考值,ArUco 图标和圆形合作标识的半径均为3.7cm,相机的图像传输参数为720p 分辨率和30fps。由于相机没有配置云台,因此运动抖动较为明显,相对位置解算的难度较大。
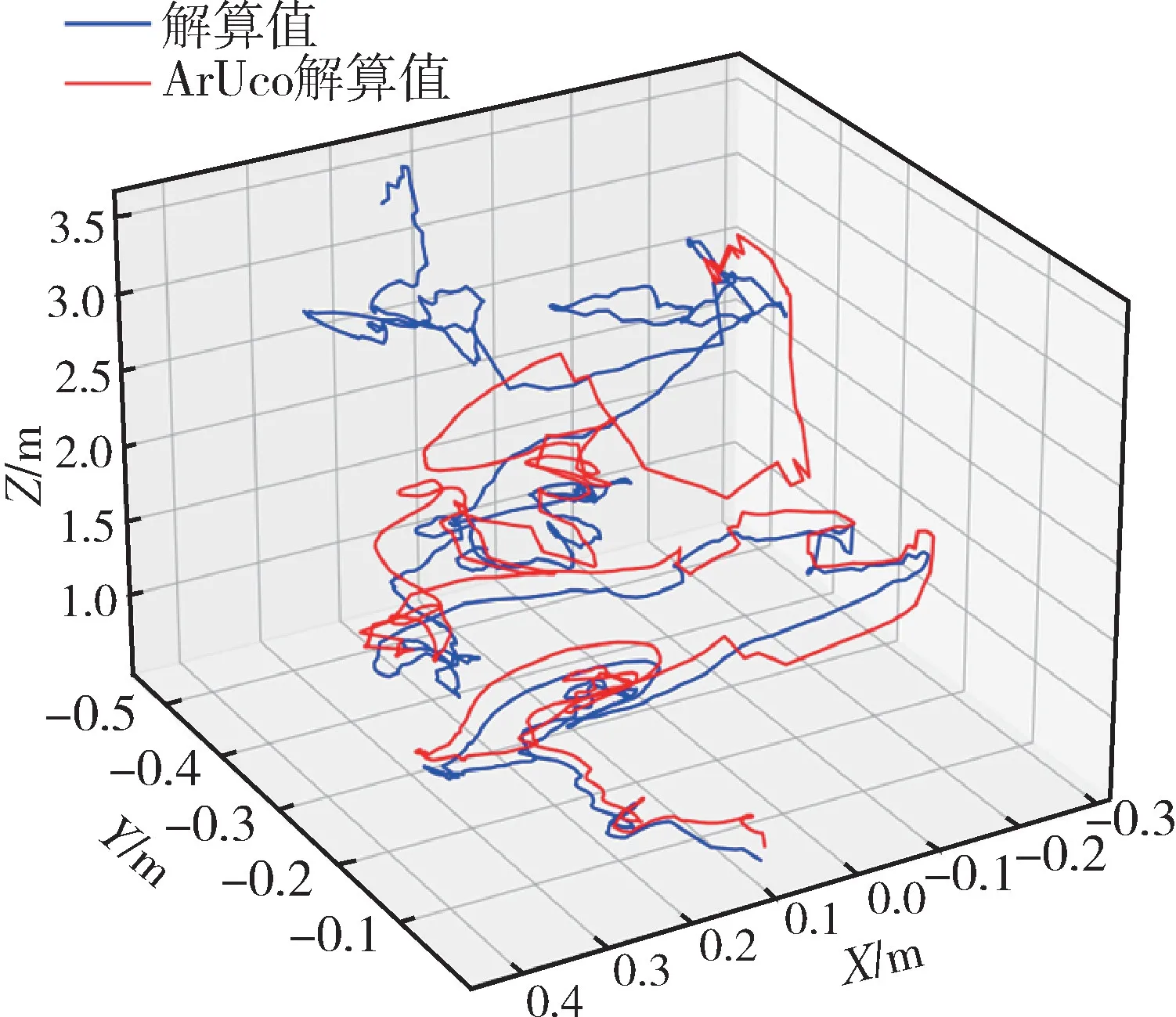
图6 卫星拒止条件下相对运动轨迹Fig.6 Relative motion trajectories under satellite rejection condition
对比图6中本文方法解算的轨迹和ArUco 位置算法解算的轨迹可知,尽管相机运动存在明显的抖动,两个算法都能较好实现对相机运动的跟踪。本文方法解算的轨迹在近距离时基本与ArUco 位置解算轨迹贴合,说明本文方法的相对位置精度在近距离时与ArUco 位置解算算法相近,而基于ArUco 位置解算算法在近距离时精度是厘米级的,因此本文方法在近距离时的位置估计可以满足相对导航要求。通过分解位置信息在X方向、Y方向和Z方向上的量及计算两个算法在这三个方向上的差值,分别如图7(a)、图7(b)和图7(c)所示。在最开始几帧,本文方法解算的三个方向位置均有不同程度抖动,这是因为算法正在初始化,由此带来位置估计的抖动可忽略不计。

图7 卫星拒止条件下相对位置解算结果Fig.7 Relative position calculation results under satellite rejection condition
通过观察位置在三个方向上的分量,可得知两个算法在X方向、Y方向上的解算基本贴合,差值<0.05m,而在Z方向上的解算趋势仍然贴合,但差值相对较大,差值<0.2m。在远距离时,发现当Z方向距离为2.5m 左右时,ArUco 方法解算在三个方向上的分量均有不同程度的抖动,且与本文方法的差值开始急剧增加,此时ArUco 方法解算的相对位置精度降低明显,而此时本文方法仍然保持较好的鲁棒性。当Z方向距离大于2.5m时,ArUco 方法已经完全无法检测ArUco 图标,从而无法解算相对位置信息,而此时本文方法仍在鲁棒地检测圆形合作标识并解算相应的相对位置信息。在室内实验场景下,图标半径为3.7cm 时,本文方法在近距离相对位置解算的精度能达到与基于二维码相对位置解算方法相同的精度,在较远距离且基于二维码相对位置解算方法失效后,仍能鲁棒地解算相对位置。
通过对比本文所提方法的相对位置解算值(蓝色实线)与基于二维码ArUco 的相对位置解算值(红色实线)可知: 1)在相对距离较近的情况下,本文方法与基于二维码ArUco 的方法都能够较好地跟踪相机运动,两种方法的解算精度相当且达到厘米级;2) 在相对距离较远的情况下,基于二维码ArUco 的方法会失效,而本文方法仍能够较好地跟踪相机运动,且具有较好的鲁棒性。
4 结论
本文针对基于椭圆特征相对位置估计存在二义解的问题,在空地无人系统相对导航场景下分析了二义解成因及其内在几何约束,提出基于特征点的相对位置初始化配准和基于连续运动约束的相对位置跟踪算法,实现了对相对位置解的稳定跟踪。在此基础上,进行了卫星拒止条件下场景下的验证。卫星拒止条件下的实验结果表明,本文方法与基于二维码ArUco 方法相比,在相对距离较远的情况下仍能够较好地跟踪相机运动,保证了相对位置估计的精度及鲁棒性。
