轴向磁通电励磁发电机绕组排布方式电磁特性分析
2023-05-19李林涛史立伟李法成王文强刘政委
李林涛,史立伟,李法成,王文强,刘政委
(山东理工大学 交通与车辆工程学院,山东 淄博 255049)
随着现代社会的发展,汽车成为日常生活中不可或缺的一部分。然而传统内燃机排出的废气不仅对环境造成了不可逆的污染,也大大浪费了其可利用的剩余能量[1]。回收废气能量,不仅可以降低对环境的污染,也最大限度地节省了化石能源的利用与消耗,成为国内外学者研究的热点与方向。
实际上,内燃机燃料燃烧主要转化为有用的机械能、废气能量、散热损失能量与机械损失能量。但机械能的转化率非常低,仅有30%~40%,而废气带走的能量占总能量的25%以上[2]。为了利用废气中的剩余能量,直接涡轮复合发电系统[3]应运而生。该系统结构简单,所需附加附件较少,受到广大学者的关注。高温高速是涡轮增压器典型的工作环境,这在很大程度上限制了发电机类型的选择。稀土永磁电机效率高、功率因数高,成为最常用、研究最为广泛的电机类型[4-5]。然而永磁体高温退磁、不易调磁与故障灭磁的特点也是其无法忽视的缺点,这也极大地限制了永磁类电机在高温场合中的应用。文献[6]把轴向磁通永磁发电机安装在涡轮膨胀机的一侧,这无疑会较大增加涡轮增压器的体积,而且对其安装位置有较高要求,同时隔热材料与冷却系统也是必不可少的。因此,电励磁类电机以其调磁方便、结构简单、稳定性高等优点脱颖而出[7-8]。GE公司与Honeywell公司分别研制了一种6/4极高速开关磁阻起动发电机,其发电运行转速分别可达50 000 r/min和60 000 r/min[9-10]。二者作为高速发电机,其共性是转子结构简单、稳定性高、散热性好。而把传统径向电励磁电机直接应用于涡轮复合发电系统时,会因转子质量大而导致涡轮增压器响应延迟的问题。因此该系统所使用的发电机需具备转子结构简单、稳定性高、质量小的特点。
针对上述问题,本文提出一种轴向磁通双定子双凸极电励磁发电机(axial flux doubly stator doubly salient electro-magnetic generator, AFDS-DSEG),用励磁绕组提供磁动势,避免了永磁体退磁的风险。转子结构简单、稳定性高,适合高温高速的工作条件,并且整体质量轻,转动惯量小,对涡轮机的响应影响较小。本文主要对该发电机定转子极数的约束公式进行推导,并通过有限元软件对AFDS-DSEG两种绕组排布的电磁特性进行分析研究。
1 AFDS-DSEG工作原理
AFDS-DSEG为单转子双定子结构,转子为分块结构,位于两定子中间,且固定在不导磁的转子套上,如图1所示。定子极与转子极均为扇形极,定子槽为扇形槽,因此定子极与转子极始终以线接触啮合与脱离,以确保电枢磁链可以均匀增加、均匀减少。电枢绕组为集中绕组,绕制在定子1上;励磁绕组为跨两极绕制,绕制在定子2上。
相比于径向磁通发电机,该发电机的转动部分只有分块转子及不导磁铝制转子套,有转动惯量小的优点;并且转子结构简单,稳定性高,适合高温高速的工作环境。
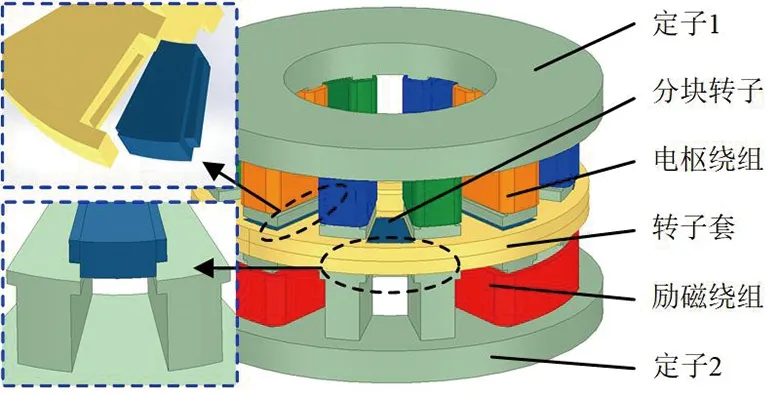
图1 AFDS-DSEG基本拓扑
图2所示为三相AFDS-DSEG发电机中间半径处轴向截面磁通路径示意图。向缠绕在定子2上的励磁绕组中通以恒定的直流电,在励磁定子中建立励磁磁场。

(a)定转子对齐
当转子齿处于图2(a)所示的位置时,转子对齐A相,磁通经转子齿在A相内匝链产生感应电动势。但此时磁通会在相邻的异极性励磁极间相互匝链,形成漏磁通。转子逆时针旋转时,转子与A1重合面积逐渐减小,与B1的重合面积逐渐增大。当转子处在图2(b)所示的位置时,磁通经A相与B相后形成磁通回路,此时磁路中有两相磁链发生变化。在转子旋转过程中,一相磁链增多,一相磁链减少,未匝链的一相磁链不变。磁链减少产生正的感应电动势,磁链增大产生负的感应电动势,经全桥整流电路后,输出电压为一定值。
图3给出了三相AFDS-DSEG的理想电感与感应电动势变化曲线。在转子旋转过程中,根据电枢绕组匝链的磁通具有周期性的特点,一个周期内电枢绕组与励磁绕组的互感可以分成三个阶段。在120°电角度时,转子齿与C相绕组所在定子齿恰好完全脱离,C相定子齿与转子槽对齐,当转子继续旋转,C相定子齿仍然与转子槽对齐,此时C相电感LCF处于最小值且保持不变;在240°电角度时,转子齿与C相所在定子齿即将出现重合部分,随着转子旋转,C相电感LCF逐渐增加,此时C相绕组内感应出负的感应电动势,直至定转子完全重合时,LCF达到最大值;当转子继续旋转,与C相完全重合的转子齿开始与定子齿脱离,C相电感LCF开始减小,在减小的过程中,绕组内感应出正感应电动势,直至完全脱离到最小值,如360°电角度时刻所示。

图3 理想电感与感应电动势曲线
2 AFDS-DSEG拓扑结构分析
上述分析足以证明,转子相对于电枢定子的位置对电枢电感有较大影响,在定转子极弧宽度相同的情况下,定转子极数是其相对位置的唯一影响条件。两定子共同构成一条磁路,对励磁定子与电枢定子分别进行分析。
假设励磁定子数为
Pse=2ik,
(1)
式中:i为励磁跨距;k为正整数。电枢定子数为
Psa=qt,
(2)
式中:t为相数;q为正整数。
由图3可知,每转过一个转子极距,电枢绕组内感应出一个周期的感应电动势,因此电枢定子上相邻的两相相差的机械角度应为
(3)
式中Pr为转子极数。一个励磁定子极、一个电枢定子极和一个转子极极距所占的机械角度分别为
(4)
以A相和C相为例,其相对位置关系如图4(a)所示,二者相差的机械角度应为
βsa-βr=±βδ,
(5)
联立式(2)—式(5),可以得出
Pr=q(t±1)。
(6)
电枢绕组反电势的产生是电枢绕组中匝链了来自励磁绕组产生的磁通,并且双侧定子对齐可以增大转子与电枢绕组完全重合时的最大磁通量Ψmax以提高电压幅值,同时保证各相工作电角度为360°/t。因此与A3和C2绕组相对应的两励磁定子齿与转子的相对位置如图4(b)所示,二者相差的机械角度应为
βse-βr=±βδ,
(7)
联立式(2) —式(4)和式(7),可以得出
(8)
即
(9)

(a)电枢定子与转子位置关系
式中:ik=tn;n为正整数。因此,定转子极数分别为
(10)
根据上述分析,表1给出了不同相数与不同励磁跨距的定转子极数。

表1 不同相数与不同励磁跨距的定转子极数
3 AFDS-DSEG电磁特性仿真分析
双定子为镜像结构,定子齿对齐,励磁绕组与电枢绕组分别按照一定的次序缠绕在定子齿上。当励磁绕组跨两个定子齿绕制时,相邻的励磁绕组绕向相反,使其N极和S极交替分布,在磁通路径上有短磁路的效果。电枢绕组为非叠集中绕组,相隔90°机械角度的四个线圈串联为一相,共有三相,各相按照ABC的顺序排列。AFDS-DSEG的基本参数见表2。

表2 AFDS-DSEG基本参数
在对AFDS-DSEG电感特性与定转子极数分析的基础上,本文利用有限元软件,保证电机主要结构与电磁参数相同的前提下,提出了两种电枢绕组与励磁绕组的排布方式,分别为励磁跨距1(excitation span 1, ES1)和励磁跨距2(excitation span 2, ES2),二者拓扑结构如图5所示。两种绕组均按照上述绕向与连接规则进行排布,建立发电机的三维拓扑模型,并着重分析三相12槽8极两种绕组排布方式的空载与负载的电磁特性。

(a)ES1 (b)ES2
该发电机旋转部分包括分块转子和转子套,二者合计质量为371.85 g,同尺寸径向磁通发电机旋转部分仅有转子,其质量为3 017.57 g,AFDS-DSEG与传统径向发电机相比质量下降了87.68%。
3.1 空载发电分析
根据表2 所列AFDS-DSEG的基本参数建立有限元仿真模型,设置仿真条件为:励磁电流为5 A,转速为3 000 r/min,对两种绕组排布进行空载发电仿真,空载感应电动势如图6所示。

图6 电枢绕组空载感应电动势
由图6可知,两种绕组排布方式感应电动势的变化基本符合图3分析中的波形,各相磁链上升、下降与不变所占的电角度均为120°。
电励磁双凸极发电机的定转子均为凸极结构,其内部磁场非线性严重,这也导致了其谐波磁场的产生,进而产生了谐波电势,谐波电势又会给直流输出电压带来较大的脉动,降低发电质量。因此谐波问题对发电机的结构设计至关重要。为了比较两种绕组排布方式对AFDS-DSEG空载感应电势的影响,对其空载感应电动势波形进行傅里叶分解,得到其各谐波阶次感应电动势幅值,如图7所示。ES1的基波幅值为6.27 V,ES2的基波幅值为5.78 V。尽管ES2的基波幅值相较于ES1有7.81%的降低,但其各次谐波相较于ES1也均有所降低。

图7 ES1与ES2空载感应电动势谐波对比
ES2有6套励磁绕组,而ES1有12套励磁绕组,相邻两套励磁绕组极性相反。当转子对齐异极性定子槽时,会引起漏磁通的闭合,如图2(a)所示。8个分块转子中,4个对齐定子齿时,会有4个对齐定子槽。ES1中这4个定子槽全都是异极性定子槽,ES2中只有两个异极性定子槽,持续性的磁通闭合又会引起铁芯损耗的增加,如图8所示。

图8 铁芯损耗对比
为了比较两种绕组排布方式空载感应电动势波形的正弦度,本文选取了空载感应电动势的前10次谐波进行谐波失真分析,通过式(11)可以分别计算出总谐波失真(UTHD)、奇次谐波含量(UTHDO)和偶次谐波含量(UTHDE)。
(11)
式中:i为谐波次数;ui为感应电动势的第i次谐波幅值。由式(11)得出的两种绕组排布方式的空载电动势各阶次谐波含量见表3。由表3可以得出,ES2相较于ES1总谐波失真下降了5.17%,奇次谐波含量下降了7.14%,偶次谐波含量下降了3.53%。因此ES2排布方式的谐波失真更少,波形正弦性更好,谐波含量少,可以有效地降低谐波所造成的损耗,提高了发电机的发电质量与功率。

表3 ES1与ES2空载感应电动势谐波含量
3.2 负载发电分析
图9为定转子相同的情况下,在励磁电流为6 A,转速为3 000 r/min,接入15 Ω纯阻性负载时,两种绕组排布的感应电动势对比图。由图9可知,整体上二者波形均为正弦型,但均出现了由于电枢反应所导致的正负幅值不对称的问题,这致使负向幅值稍大于正向幅值。

(a) ES1
为了进一步评估负载感应电动势波形的畸变情况,对负载感应电动势波形进行傅里叶分解后,取其前10次谐波进行分析,如图10所示。ES2相较于ES1基波幅值下降了0.61 V,除此之外,其他各阶次谐波也均有不同程度的降低。依据式(11)可计算得出具体降低量,见表4。

图10 ES1与ES2负载感应电动势谐波对比
由表4可知,ES2总谐波失真比ES1下降了5.07%,并且其奇次谐波与偶次谐波均有所下降,因此ES2感应电动势波形中的总谐波失真少,谐波含量减少,发电机的发电质量较好,效率较高。
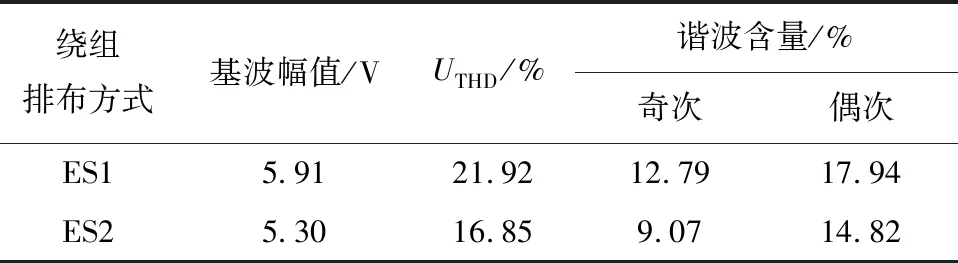
表4 ES1与ES2负载感应电动势谐波含量
负载的输出电压如图11所示,其中ES1与ES2的输出电压均值分别为8.33 V和7.15 V,脉动率分别为58.60%和42.17%。这说明ES2还有输出脉动率低的优点。

图11 ES1与ES2输出电压对比
4 结论
本文提出了一种轴向磁通电励磁双凸极发电机,介绍了发电机的基本拓扑结构与发电原理,并对该发电机定转子极数进行推导,对两种绕组排布方式进行仿真分析,得到如下结论:
1)AFDS-DSEG在设计时,其电感应对称,总磁导应保持不变,其相数与励磁跨距应满足表1中的约束条件。
2)与ES1相比,ES2的漏磁路径少,损耗较少;空载时,ES2的感应电动势总谐波失真相较于ES1下降了5.17%,负载感应电动势总谐波失真下降了5.07%。因而,ES2绕组排布方式正弦度较高,谐波含量较少,输出电压脉动小,发电质量较好。
