矩相关保费原理下具有时间变化效应的信度模型
2023-05-19李新鹏高榕陈一峰万萌萌何爱进吴黎军
李新鹏,高榕,陈一峰,万萌萌,何爱进,吴黎军
(1.新疆农业大学 数理学院,新疆 乌鲁木齐 830052;2.新疆大学 数学与系统科学学院,新疆 乌鲁木齐 830046)
信度理论是保险精算中重要的保费厘定方法,它依据风险的先验信息和赔付信息对保费进行估计,得到的信度保费为样本均值和信度补项的加权平均。Bühlmann等[1]研究的任意分布下的净保费信度估计是现代信度理论起源。
若保险人只收取净保费,则依据破产理论,必将导致保险人破产,所以在实际中不能直接使用净保费原理。因此,在不同保费原理下对信度保费的研究成为其热门领域,Bühlmann[2]研究了基于方差保费原理的近似信度估计;Pan等[3]给出了Esscher保费原理下的信度估计,并证明了估计满足相合性;温利民等[4]研究了基于指数保费原理的信度保费;章溢等[5]在2019年采用风险随机变量的矩母函数给出了矩相关保费原理,它包含了非寿险精算学中大部分保费原理,研究了矩相关保费原理下信度保费问题;李新鹏等[6]在2021年研究了基于矩相关保费原理的具有风险相依结构的信度保费问题,给出了信度保费以及结构参数的无偏估计。
在实际问题中,不同风险之间具有相关性,如一次交通事故可以导致多个赔付,地域相近的房屋面临共同的火灾风险等。李新鹏等[7-8]在LINEX损失函数下分别对具有时间变化效应的单合同和多合同信度模型问题进行了研究,推导出了相应的信度保费;Bolancé等[9]提出了索赔频率风险模型,推导出了时间效应为自相关时间序列时的信度保费;郑丹等[10]研究了具有时间变化效应的信度保费问题;Wen等[11]研究了共同随机效应下的信度模型,得到了信度保费;李新鹏等[12]在2020年给出了MLINEX损失函数下具有风险相依效应的信度保费。
本文在矩相关保费原理下,考虑风险间的时间变化效应,研究一份保单在过去不同年赔付额之间具有时间变化效应的信度模型,以期得到相应的信度保费,最后,运用数值模拟的方法验证基于矩相关保费原理,并证明几种常见保费原理下风险保费的信度估计满足相合性。
1 模型假设与预备知识
信度理论基于平方损失函数,将估计限定在过去赔付额的线性组合中,得到信度保费公式

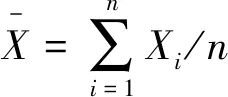
给定随机变量X,称M(t)=E(etX)为随机变量X的矩母函数。由此可得
E(X)=M'(0),
D(X)=M''(0)-[M'(0)]2,
E(eαX)=M(α),
E(XeαX)=M'(α),
并且定义一种统一的保费原理——矩相关保费原理。
定义1给定风险随机变量X及数α>0,矩相关保费原理为
H(X)=f(M'(0),M''(0),M(α),M'(α)),
式中f为多元连续函数[5]。
假设一份保单过去n年赔付额随机变量X1,X2,…,Xn有各自的风险参数Θ1,Θ2,…,Θn,且这些风险参数具有时间变化效应。模型的假设如下:
假设1给定风险参数Θ1,Θ2,…,Θn,赔付额X1,X2,…,Xn之间独立, 条件矩母函数为
M(t,θi)=E(etXi|θi),i=1,…,n+1。
由此可得:
假设2风险参数Θi的分布函数为π(θi),且
E[M(t,θi)]=M0(t),
Cov[M(t,θi),M(t,θj)]=
εi(t)εj(t),i,j=1,…,n+1。
记X=(X1,…,Xn)',Θ=(Θ1,…,Θn)'。易知:
E(Xi|θ)=M'(0,θ),
D(Xi|θ)=M''(0,θ)-[M'(0,θ)]2,
E(eαXi|θ)=M(α,θ),
E(XieαXi|θ)=M'(α,θ)。
基于矩相关保费原理,该保单下一年的风险保费为
u(θ)=f(M'(0,θ),M''(0,θ),M(α,θ),M'(α,θ)) ,
(1)
为此,令
Yi(t)=etXi,Y(t)=(Y1(t),…,Yn(t))'。
令Yi(t)的线性组合为M(t,θ)的估计,通过求解下述最优化问题:
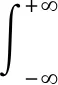
(2)
式中ω(t)≥0为已知权重函数,得到其估计,再依据“代入”准则得到u(θ)的信度估计。
为了求解问题(2),给出引理1。
引理1设Yn+1(t),Y1(t),…,Yn(t)为随机序列,Y(t)=(Y1(t),…,Yn(t))',B=(b1,…,bn),则当
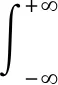
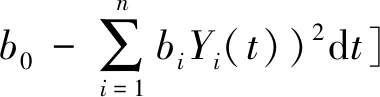
引理2给出了具有时间变化效应的信度模型的性质。
引理2在假设1和假设2下,可得以下结论:
(i)Yi(t)的期望为
E[Yi(t)]=M0(t),i=1,…,n+1。
(ii)Yn+1(t)与Y(t)的协方差为
Cov[Yn+1(t),Y(t)]=
εn+1(t)(ε1(t),…,εi(t),…,εn(t))。
(iii)Y(t)的方差协方差矩阵为
i=1,…,n)+(ε1(t),…,εi(t),…,
εn(t))'(ε1(t),…,εi(t),…,εn(t)),
式中diag[…]为对角矩阵。
(iv)Y(t)的方差协方差矩阵的逆矩阵为

2 矩相关保费原理下信度保费估计
下述定理1给出了问题 (2) 的解,即条件矩母函数M(t,θ)的最优估计。
定理1在假设1、假设2下,通过求解最优化问题(2),得到M(t,θ)的最优估计为
式中:

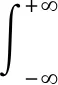
证明由引理1得,M(t,θ)的最优估计为
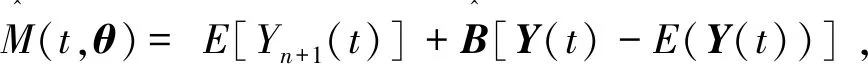
(3)
根据引理2和定理1中已知条件可得
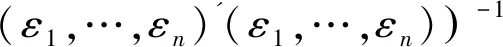
因此,


令
E(Xi|θ)=μ1(θ),
E(XieαXi|θ)=γ(α,θ),
E[μ1(θ)]=μ1,
E[μ2(θ)]=μ2,
E[γ(α,θ)]=γ(α),
并且引入记号
则风险保费为
u(θ)=f(μ1(θ),μ2(θ),M(α,θ),γ(α,θ))。
因此,通过“代入”原则,易得定理2。
定理2在矩相关保费原理下,基于风险之间的时间变化效应,得到矩母函数的信度估计,进而得到风险保费u(θ)的信度估计为
式中:
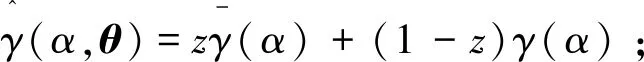
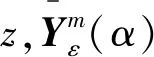
由于函数f具有不同形式,所以根据定理2给出期望值保费原理、方差保费原理、Esscher保费原理、指数保费原理下具有时间变化效应的信度保费估计。
推论1(i)期望值保费原理中信度保费估计为
(ii)方差保费原理中信度保费估计为
(iii)Esscher保费原理中信度保费估计为
(iv)指数保费原理中信度保费估计为
推论2在矩相关保费原理下,基于风险之间的时间变化效应,Bühlmann模型的信度保费估计为
式中:
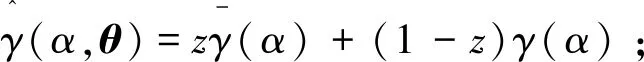

3 数值模拟
下面运用数值模拟方法验证基于矩相关保费原理,证明在几种常见保费原理下本文得到的信度保费估计满足相合性。
首先,给出期望值保费原理、方差保费原理、Esscher保费原理、指数保费原理下风险保费分别为:
u1(θ)=(1+α)μ1(θ),
u2(θ)=μ1(θ)+α(μ2(θ)-μ1(θ)2),
假设Θi~U(0,0.5),在风险参数θi给定下,赔付额Xi,i=1,…,n+1服从Bernoulli分布,即P(Xi=1|θ)=θ,P(Xi=0|θ)=1-θ,则:
M(α,θ)=E(eαXi|θ)=θ(eα-1)+1,
σ2(α,θ)=D(eαXi|θ)=(eα-1)2(θ-θ2),
μ1(θ)=μ2(θ)=θ,
γ(α,θ)=E(XieαXi|θ)=θeα,
取
εi(α)=εj(α)=ε(α),

则


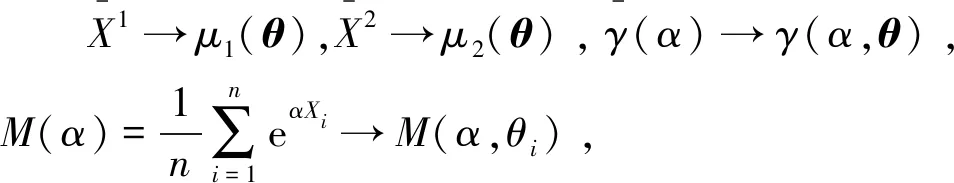
根据定理2及连续性定理可得

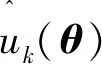

表1 不同样本容量下风险保费的信度估计均值及均方误差
从表1可看出,4种保费原理下得到的风险保费信度估计的均方误差随着样本容量的增大而逐渐减小,说明本文得到的信度估计满足相合性。
4 结束语
本文在矩相关保费原理下,研究了具有时间变化效应的信度保费,得到了信度估计,并且给出了基于矩相关保费原理和几种常见保费原理下具有时间变化效应的信度保费估计和具有时间变化效应的Bühlmann模型的信度保费估计。本文得到的信度估计形式简单,数值模拟验证了本文得到的信度估计满足相合性。
