基于B样条算法的智能车辆局部避障路径规划
2023-05-19张宇龙杨金山王鹏伟黄炯肖文龙
张宇龙,杨金山,王鹏伟,黄炯,肖文龙
(1. 山东理工大学 交通与车辆工程学院,山东 淄博 255049;2.江铃汽车股份有限责任公司,江西 南昌 330001)
智能车辆局部路径规划常用方法包括人工势场法[1]、贝塞尔曲线法[2]、遗传算法[3]、B样条曲线算法[4]等。由于这些方法提出年代较早,在现代应用中难免存在计算复杂、效率低下等缺陷,为此,学者提出多种改进方案[5]。杨杨等[6]在传统人工势场算法的基础上引入速度势场函数,把横、纵向危险影响范围设定为不同值,保证车辆避障路径满足车辆动力学要求。张新锋等[7]提出了一种基于贝赛尔曲线的轨迹规划算法,并且对路径的最大曲率与目标状态曲率进行约束,规划出一条曲率连续有界的避障路径。徐美清等[8]将神经网络与遗传算法相结合,使用遗传算法特性来调整神经网络中的权值,从而保证在未知复杂道路上规划出一条顺利避开障碍物的较优路径。屈盼让等[9]通过建立完整的分布规划模型对B样条曲线算法进行改进,最终得到最优规划路径,且路径生成高效,满足实时规划路径的要求。在众多路径规划算法中,B样条曲线算法作为一种典型的多项式曲线,其规划路径平滑性好,且计算原理简单,计算量小,符合路径规划系统对算法实时性的要求,深受学者关注。
因此,针对无人车实际局部避障情况,本文提出基于三次准均匀B样条算法的路径规划方案。通过在传统B样条算法中引入无碰撞约束与车辆动力学约束条件,确定控制点,生成满足要求的规划路径,并采用CarSim与Matlab联合仿真验证路径合理性。
1 基于B样条曲线算法的路径规划
1.1 B样条算法概述
B样条曲线是在贝塞尔曲线基础上推导而来,该曲线是Schoenberg于20世纪40年代提出的,由De Boor和Cox分别提出的递推定义[10],通过控制点与B样条基函数组合生成曲线形状。本文采用三次准均匀B样条曲线进行路径规划,因其两端节点有重复度k,使曲线起始于第一个控制点,终止于最后一个控制点。规划路径时,先确定智能车辆进行避障过程中的碰撞约束、动力学约束等条件,保证车辆顺利躲避障碍物,再根据上述条件选取控制点,最后通过控制点与B样条基函数结合得到符合要求的避障路径。
曲线、控制点与B样条基函数具体关系如下。假定P0,P1,P2,…,Pn一共n+1个控制点对B样条曲线进行控制,则k阶B样条为
(1)
式中:Bi,k(u)表示第i个k阶B样条基函数;u为自变量。
B样条基函数的递推公式为
(2)
式中ui为第i个节点,所有节点组成非递减序列的节点向量U=[u0,u1,…,umax][11]。
在式(2)中约定:

(3)
1.2 选取控制点
智能车辆局部避障路径规划过程由障碍物检测、信息处理、避障路径生成三部分组成。智能车辆使用车载传感器检测周围环境信息,并确定车辆位姿信息。信息处理器综合所有信息,通过分析影响避障的因素,确定当前存在的安全隐患,进而采取合适的避障策略规划最优避障路径。
设定行驶道路是直行双车道,智能车辆在一侧道路中心线上行驶,当检测到前方障碍车后,需行驶到另一侧道路,以躲避障碍车,并在完成避障后返回原车道行驶。设定智能车长为h0、宽为m0,障碍车长为h1,宽为m1,并分别简化为m0×h0与m1×h1的矩形。道路可行驶区域设定为长为L,宽为2r的矩形,两条车道由虚线分隔。将道路环境放在二维坐标系下,如图1所示,A1表示智能车,A2表示障碍车。车辆行驶过程中车身要在道路边界之内,以保证不与道路边界碰撞,则B样条控制点位置(x,y)选取范围为

(4)
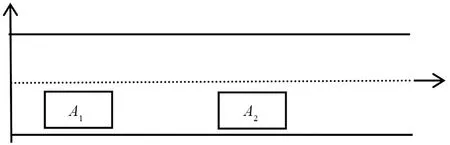
图1 道路约束示意图
此外,车辆经过障碍车恰好不碰撞的临界位置如图2所示,需保证车辆经过该位置外,以避免碰撞发生。
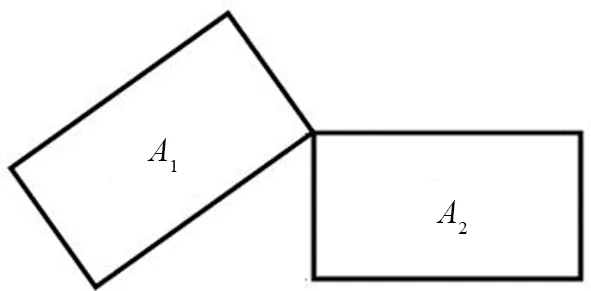
图2 智能车辆不与障碍车碰撞的临界示意图
则智能车与障碍车纵向初始安全距离限制为
D≥xA1-xA2,
(5)
式中:xA1为智能车纵向位移;xA2为障碍车纵向位移。
为避免智能车辆避障过程中发生侧滑,需设定车辆动力学约束:
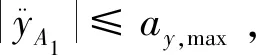
(6)
式中:yA1为智能车辆横向位移;ay,max为智能车辆最大侧向加速度。
避障路径规划过程中需要考虑障碍物位置、尺寸、速度等因素。为保证车辆避障系统出现失误后有足够的距离刹车,不与障碍物发生碰撞,本文设定在躲避障碍物过程中,避障初始位置由TTC碰撞时间与当前车速结合确定。基于本文研究智能车辆,计算TTC时间时不需要考虑与驾驶员有关的影响因素。则TTC时间为车辆持续产生制动力到车辆速度减至与障碍车速度相同所需时间以及制动生效到液压器产生制动的时间之和。假定持续制动过程中车辆保持最大制动加速度,该过程所花费的时间为
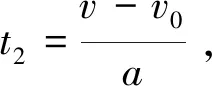
(7)
式中:v是智能车辆行驶速度;a是智能车辆制动加速度(取7.84 m/s2);v0是障碍车速度(静态障碍车速度取0)。
假定在制动生效到液压器产生制动的时间内,车辆速度不变,则实现车辆与障碍物之间不发生碰撞的安全距离为

(8)
式中t1是制动生效到液压器产生制动的时间,该时间大约为0.15~0.3 s[12],本文取0.2 s。
采用此种方法得到的安全距离会随智能车辆车速降低而减少,为避免低车速时转弯半径过小,智能车难以稳定进行避障操作,本文在安全距离之外加入一段调节距离z,经过多次实验得出调节距离与车速关系为
(9)
假定智能车开始避障时,障碍车尾部中心点初始位置是(x1,-0.5r),则第一个控制点为P0=(x1-x0-z,-0.5r)。同时,为满足初始时刻智能车辆航向角为零且不发生突变,设定P2=(x1-x0-z+d,-0.5r),为进一步加强该约束,设定控制点P1=(x1-x0-z+0.5d,-0.5r)。d取值过大易造成避障换道过程中纵向距离不足,难以满足车辆动力学约束,故设定d与智能车辆车长相同。
智能车保持原速行驶,从与障碍车距离为x0到不与障碍车发生碰撞的临界位置时,障碍车行驶距离为

(10)
从而得到临界位置时,障碍车尾部横坐标为x1+x2,如果智能车辆车头横坐标位于x1+x2时,能运行到另一侧道路中心线处,智能车将与障碍车、路边均有足够安全距离,且该过程中智能车辆横向位移较小,能保证侧向加速度在合理范围内,故选定控制点P3=(x1+x2,0.5r)。
智能车换道后一直沿另一侧道路中心线行驶,当智能车辆车尾处横坐标超过障碍车的车头横坐标半个车身长度时,智能车辆进行返回原车道的操作,以此确保返回过程中不与障碍车发生碰撞。忽略智能车辆换道过程中多消耗的时间,则智能车辆从行驶至避障道路中心线到上述位置所用的时间为

(11)
则进行转向操作的横坐标位置为
x3=x1+x2+vt3,
(12)
因此选取控制点P4=(x1+x2+0.5vt3,0.5r)、P5=(x3,0.5r),将返回原车道的路径设定为与避障路径对称的状态,故选取控制点P6=(x3+x0+z+x2-d,-0.5r)、P7=(x3+x0+z+x2-0.5d,-0.5r)、P8=(x3+x0+z+x2,-0.5r)。
2 仿真验证
为验证路径规划方案合理性,运用CarSim与Matlab进行联合仿真。首先,在Matlab中得出不同工况下的规划路径;其次,设置CarSim中的仿真场景,将CarSim中信息发送到Matlab/Simulink,由Simulink横向控制模块控制车辆沿规划路径行驶,并观测车辆动力学参数波动范围。
2.1 躲避静态障碍车的规划路径
设置智能车辆与障碍车的宽为2 m,长为4.79 m,仿真车道单条车道宽度为3.5 m,长度为100 m,路面摩擦系数设置为0.85。在静态避障场景中,静止障碍车尾部横坐标设置于50 m处。智能车辆分别以10 m/s与15 m/s的速度躲避静止障碍车的路径如图3、图4所示,其中红色矩形为障碍车简化模型,绿色曲线为规划路径。
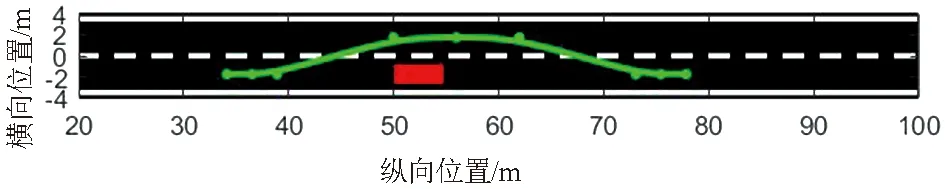
图3 车速恒定10 m/s躲避静止障碍车
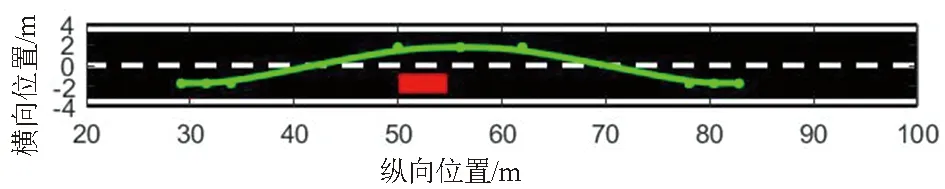
图4 车速恒定15 m/s躲避静止障碍车
图3、图4表明在此场景下智能车能够躲避静止障碍车,并且成功返回原车道行驶,证明规划路径适用于此种工况。
路径平滑性主要根据路径曲率求得,车速恒定10 m/s时躲避静止障碍车工况下的规划路径曲率波动范围为-0.038 0~0.068 0 m-1,车速恒定15 m/s时为-0.027 4~0.042 3 m-1。该结果表明路径曲率变化幅度较小,平滑性较好。
2.2 躲避动态障碍车的规划路径
在动态避障场景中,低速障碍车速度设置为5 m/s,并且当障碍车运行到车尾横坐标为50 m时,智能车辆正好到达应该进行避障操作的位置。得出智能车辆分别以15 m/s与20 m/s的速度躲避障碍车的路径如图5、图6所示,其中蓝色矩形为智能车简化模型。
图5、图6表明在此场景下智能车能够躲避低速障碍车,并且成功返回原车道行驶,证明规划路径适用于此种工况。

图5 车速恒定15 m/s躲避低速障碍车
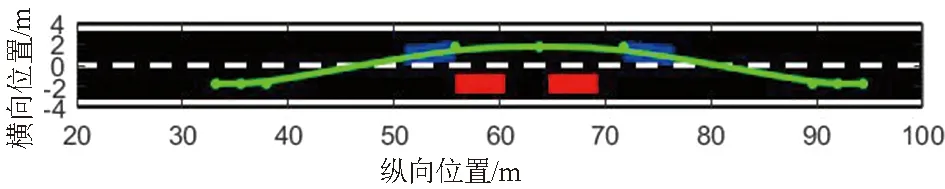
图6 车速恒定20 m/s躲避低速障碍车
车速恒定15 m/s时躲避低速障碍车工况下的规划路径曲率波动范围为-0.028 9~0.060 7 m-1,车速恒定20 m/s时为-0.018 0~0.038 2 m-1。该结果表明路径曲率变化幅度较小,平滑性较好。
2.3 路径动力学验证
根据本文设定的数据信息在CarSim中搭建仿真场景,同时结合Matlab/Simulink中基于规划路径的LQR控制模型对路径合理性进行验证。
为验证路径合理性,本文采用较高车速车辆在较低车速下规划得出的路径上行驶,观测车辆动力学参数波动情况。设定以15 m/s车速在10 m/s车速下、以20 m/s车速在15 m/s车速下、以25 m/s车速在20 m/s车速下规划出的路径行驶,得出车辆质心侧偏角、前轮转角以及横摆角速度波动范围见表1。
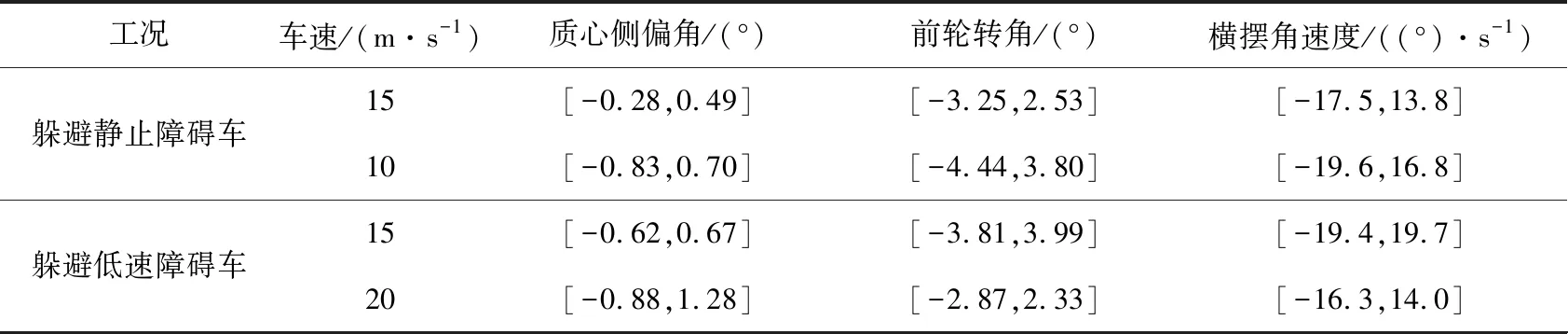
表1 不同工况下智能车辆各类动力学参数波动范围
从表1能够看出,不同工况下智能车辆动力学参数波动均在合理范围内[13-15],能够保证车辆运行过程中具有较好平顺性与横向稳定性。
3 结束语
本文对智能车辆局部避障路径规划问题进行分析,设计了一种基于B样条算法的避障路径规划方法,进而规划出不同工况下的局部避障路径。通过仿真验证不同工况下规划路径曲率及智能车辆各类动力学参数。结果表明规划路径能够满足车辆动力学约束、路径平滑、无碰撞等条件,适用于智能车辆局部避障过程。
