区域视角下我国老龄化人口的组合预测模型

孙丽苹, 袁宏俊, 胡凌云

( 1.安徽财经大学 统计与应用数学学院; 2.安徽财经大学 管理科学与工程学院: 安徽 蚌埠 233030 )

统计显示,2020年我国人口(14.11亿人)中65岁及以上人口总数为1.90亿人(占比为13.5%)[1],这表明我国已经进入老龄化社会.人口老龄化不仅会加大社会保障和公共服务压力,而且会持续影响社会活力、创新动力和经济潜在增长率,因此研究老龄人口变化具有重要意义.传统预测人口的方法主要有GM(1,1)模型[2]、Logistic模型[3]、BP神经网络模型[4]、队列要素法[5]等,这些单一模型虽然具有自我学习能力强和使用数据少等优点,但由于它们难以同时捕获数据序列的线性及非线性特征,因此在预测波动性强的数据序列时存在精度较低的问题.为此,一些学者提出了基于不同准则的定权组合模型和变权组合模型,如徐翔燕等构建的GM(1,1)-SVM组合预测模型[6]、龙会典等构建的GM(1,1)-Markov链组合预测模型[7]、袁宏俊等构建的COWG-WPA算子区间型组合预测模型等[8-10],研究表明这些组合模型的预测效果均优于单项预测模型.基于上述研究,本文以灰色-BP神经网络模型、残差修正GM(1,1)模型和Logistic模型作为单项预测模型,构建了一种基于相关系数的诱导有序加权平均(IOWA)算子组合预测模型,并利用该模型预测了2021—2030年我国东部、中部、西部和东北部地区及全国的老龄人口发展趋势.

1 老龄人口总量的单项预测模型

1.1 残差修正GM(1,1)模型

灰色理论[11]由邓聚龙教授首次提出,其中GM系列模型因具有使用数据少和计算简单等优点被广泛应用于经济、农业及交通运输等多个领域.由于修正的灰色预测模型优于GM(1,1)预测模型[12],因此本文选用修正的灰色预测模型对老龄人进行预测.构建修正的灰色预测模型的步骤如下:

(1)

(2)

(3)

(4)

(5)

其中k∈[k0,n].

(6)

其中k0指未参加残差修正的个数.

1.2 灰色-BP神经网络模型

BP神经网络模型[13]是一种能够模仿人脑结构及其功能的信息处理系统,其运算方式主要为信息前向传播和误差反向传播.由于该模型具有超强的自学习与自组织能力以及具有良好的非线性映射、容错和泛化等能力,因此被广泛应用于经济、环境科学及自动化技术等领域.研究显示,将灰色预测模型和BP神经网络模型相结合可有效提高预测的准确性[14],因此本文利用GM(1,1)和BP神经网络模型构建灰色-BP神经网络模型,构建步骤为:

步骤2 构建BP神经网络模型的输入矩阵P和输出向量y.将灰色预测值的前3年数据作为第1组样本的输入向量,再用第4年数据替换第1年数据后的数据作为第2组样本的输入向量,如此迭代即可得输入矩阵P.将实际值的第4年数据作为第1组样本的输出值,将实际值的第5年数据作为第2组样本的输出值,以此类推即可得到输出向量y.

步骤3 利用输入矩阵和输出向量构建BP神经网络模型.

步骤4 利用灰色-BP神经网络模型计算预测值,并对该模型的外推性进行验证.若误差函数值满足模型的外推性条件,则对未来数据进行预测;否则返回步骤3,调整部分参数后重新构建BP神经网络模型.

1.3 Logistic模型

2 基于相关系数和IOWA算子的老龄人口的组合预测模型

2.1 模型的建立

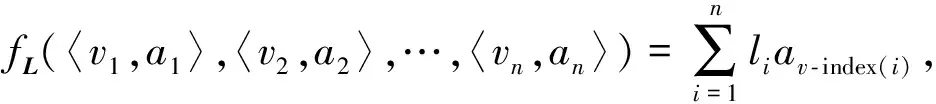
步骤1 计算第i种单项预测方法的预测精度ait,其计算公式为:

其中:i= 1,2,…,n;t= 1,2,…,N;xt为老龄人口实际值;xit为第i种单项预测方法的预测值.

步骤3 构建以相关系数最大化为准则的最优组合预测模型,权重向量L的计算公式为:

步骤5 计算未来k期的组合预测值,其计算公式为:

2.2 预测误差评价指标体系

3 老龄人口预测的实证研究

3.1 数据来源

本文选取2000—2020年《中国人口和就业统计年鉴》中31个省、自治区、直辖市的65岁及以上人口数作为研究数据(见表1),运用灰色-BP神经网络模型、残差修正GM(1,1)模型和Logistic模型进行组合预测.

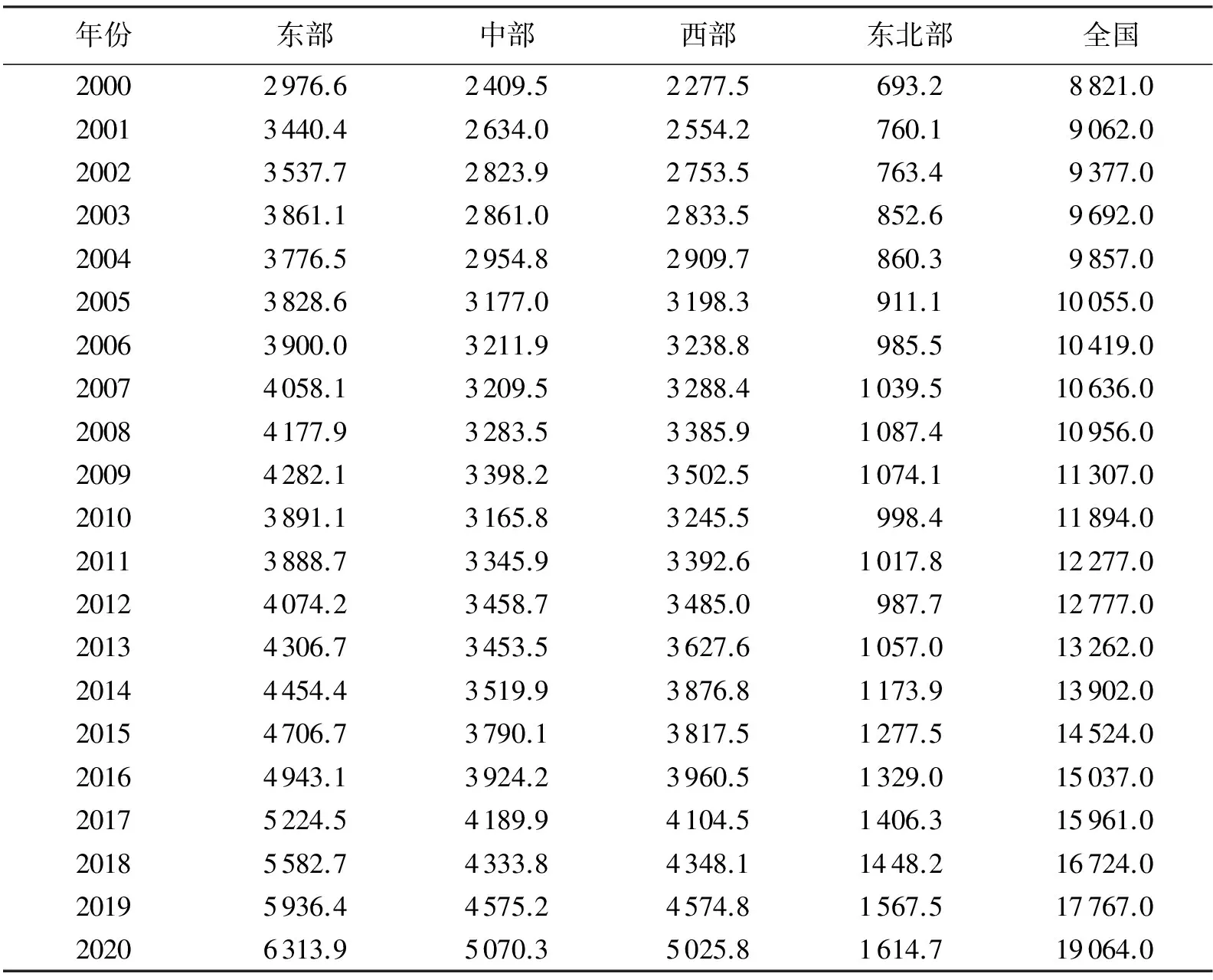
表1 各地区及全国65岁及以上老龄人口的实际数量 万人

3.2 老龄人口数的单项预测

3.2.1残差修正GM(1,1)模型的预测结果

运用所得的修正模型对各地区及全国老龄人口数进行预测的结果见表2.

表2 利用残差修正GM(1,1)模型预测各地区及全国老龄人口的结果 万人

3.2.2灰色-BP神经网络模型的预测结果

以2003—2018年数据为训练集,以2019—2020年数据为测试集构建灰色-BP神经网络模型.其中:输入层神经元数为3,输出层为1,隐含层的取值范围为3～12;输入层和隐含层之间的激活函数为tansig函数,隐含层与输出层之间的激活函数为logsig函数,训练函数为trainlm函数.利用Matlab软件计算得到的各区域及全国老龄人口数的预测结果见表3.

表3 利用灰色-BP神经网络模型预测各地区及全国老龄人口的结果 万人

3.2.3Logistic模型的构建及其预测

3.3 基于相关系数和IOWA算子组合模型的预测结果

以预测西部地区老龄人口为例建立的基于相关系数和IOWA算子的组合预测模型为:

(7)

表4 利用Logistic模型预测各地区及全国老龄人口的结果 万人

表5 利用组合预测模型预测各地区及全国老龄人口的结果 万人

为了对各预测模型的有效性进行比较评价,利用SSE、MAE、MSE、MAPE、MSPE对各预测模型的预测结果进行了检验,结果见表6.由表6可以看出:组合预测模型的各评价指标值均显著优于各单项预测模型;在3个单项预测模型中,预测精度高低的顺序依次是灰色-BP神经网络模型、残差修正GM(1,1)模型、Logistic模型.这表明,本文提出的组合模型可以有效地提高老龄人口预测的准确性.

利用本文提出的组合模型对我国东部、中部、西部和东北部地区及全国的2021—2030年老龄人口进行了预测,其结果见表7.由表7可以看出,未来10年内我国老龄人口数将保持增长的态势,其中:东部地区的老龄人口数呈持续高增长的态势,2030年将达到9860.6万人;中部地区在2021—2026年呈缓慢增长趋势,在2027—2030年则呈先下降后不断增长的趋势,其中在2029年达到峰值(7893.2万人);西部地区在2021—2023年呈缓慢增长趋势,在2023—2030年则出现先大幅增长后缓慢增长的趋势,其中在2030年达到峰值(8039.1万人);东北部地区在2021—2030年始终保持平稳增长,在2030年达到峰值(2114.4万人).这表明,我国区域间的老龄化进程差异不断增大,其中东部地区的老龄人口在未来10年的增长速度达到51.9%,而中部地区仅为24.4%.

表6 各模型预测的评价结果

表7 2021—2030年不同地区和全国老龄人口的组合预测结果 万人

4 结论

研究表明,本文提出的基于相关系数的IOWA算子组合预测模型的预测效果显著优于残差修正GM(1,1)模型、灰色-BP神经网络模型和Logistic模型,因此可利用本文模型对老龄人口进行预测.对我国东部、中部、西部和东北部地区及全国未来10年老龄人口数进行预测显示:我国老龄人口整体呈持续增长趋势,同时区域间的老龄化进程差异不断增大,其中东部地区老龄人口增长速度相对较快,中部地区则相对较慢.该研究结果可为各区域的老龄人口政策的制定提供参考.由于老龄人口数会受到经济发展、人口政策及医疗技术等各种因素的影响,因此为了达到更好的预测效果,在今后研究中我们拟将更多的因素加入到预测模型中,如人口出生率、人均地区生产总值等.