三维X型态的相干值计算

赵安婷, 方明, 陶元红

( 1.延边大学 理学院, 吉林 延吉 133002; 2.浙江科技学院 理学院, 杭州 310023 )

0 引言

量子相干性是量子力学的基本特征之一,也是量子信息学中的重要组成部分.研究表明,量子相干性在量子信息处理[1]、量子生物学[2]等领域有着重要的应用.2014年,Baumgratz等[3]提出了一个量化相干性的数学框架(BCP框架).由于该框架中的一个量化相干性条件(强单调性)难以验证,因此2016年于晓东等[4]提出了一个与BCP框架等价的YZX框架.基础YZX框架,学者们提出了大量的相干度量,如l1范数相干度量[3]、lp范数相干度量[5]、相对熵相干度量[3]、α-亲和度相干度量[6]、Tsallis-α相对熵相干度量[7]、Rényi-α相对熵相干度量[8]和斜信息相干度量[9]等.

近年来,学者们在不同相干度量下对量子态的相干性值的解析表达式进行了较多研究.对于单量子比特态,已有学者给出了其在几何相干度量[2]、迹距离相干度量[10]、保真度相干度量[10]、改进的保真度相干度量[11]以及其他7种常见的相干度量(l1范数相干度量、lp范数相干度量(p≥2)、相对熵相干度量、Tsallis-α相对熵相干度量、Rényi-α相对熵相干度量、α-亲和度相干度量和斜信息相干度量)[12]下的相干性值的解析式.针对高维最大相干混合态,有学者给出了其在几何相干度量[13]、迹距离相干度量[14]以及其他6种常见相干度量(l1范数相干度量、lp范数相干度量(p≥2)、相对熵相干度量、保真度相干度量、迹距离相干度量和斜信息相干度量)[15]下的相干性值的解析式.目前,大部分学者研究的多为两量子比特X型态,而对三维X型态的研究较少,如王耀坤等[16]只在无偏基下对这类态的l1范数相干值进行了研究;因此,本文研究如下三维X型态[16]的相干度量的解析表达式:

(1)

其中x、y、z均为非0实数.

1 基于范数的相干度量下的解析式

1)l1范数相干度量.本文记I为非相干态集合.量子态ρ的l1范数相干度量的表达式[3]为:

由l1范数相干度量的定义可知,Cl1(ρ)只与密度算子ρ的非对角线元素有关,因此显然有:

Cl1(ρX)= 2|z|.

2)lp范数相干度量.量子态ρ的lp范数相干度量的表达式[5]为:

由lp范数相干度量的定义可知,Clp(ρX)等于密度算子的所有非对角元素模的p次幂之和,因此有:

由上式可知,在lp范数相干度量下三维X型态(式(1))的相干性值的解析表达式为:

3)α-亲和度相干度量.对任意的量子态ρ和δ,其α-亲和度可定义[6]为:

量子态ρ的α-亲和度相干度量表达式[6]为:

(2)

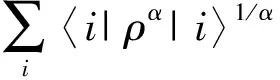
(3)

对于三维X型态(式(1)),若记

(4)

则有

(5)

再由式(2)可知,在α-亲和度相干度量下三维X型态(式(1))的相干性值的解析表达式为:

2 基于熵的相干度量下的解析式

2.1 相对熵相干度量

量子态ρ的相对熵相干度量的定义[3]为:

(6)

其中S(ρ)=-tr(ρlog2ρ)为冯诺依曼熵.为了方便计算ρX(式(1))的冯诺依曼熵,本文首先计算X型态ρX(式(1))的3个特征值.经计算,这3个特征值分别为:

基于上述计算结果和S(ρX)、S(ρXdiag)的定义可得:

S(ρX)=-tr(ρXlog2ρX)=(x+y-1)log2(1-x-y)-

S(ρXdiag)=-tr(ρXdiaglog2ρXdiag)=-xlog2x-ylog2y-(1-x-y)log2(1-x-y).

于是再由式(6)可得:

综上可得,相对熵相干度量下三维X型态(式(1))的相干性值的解析表达式为:

Cr(ρX)=xlog2x+ylog2y-

2.2 Tsallis-α相对熵相干度量

2.3 Rényi-α相对熵相干度量

3 基于斜信息的相干度量下的解析式

量子态ρ的斜信息相干度量的表达式[17]为:

(7)

为了便于相关研究人员对三维X型态的相干值进行学习与查阅,本文将上述3类相干度量下的三维X型态(式(1))的相干值的解析表达式列于表1中.在今后的研究中,我们将继续讨论高维量子态在不同相干度量下的解析表达式,以为相干性值的计算提供便利.

表1 三维X型态的相干度量的解析表达式