星载成像高度计双侧独立交叉定标方法

白卓， 张颢馨， 马纯永，2， 赵朝方，2， 陈戈，2

1. 中国海洋大学 信息科学与工程学院, 青岛 266100;2. 青岛海洋科学与技术试点国家实验室, 青岛 266237

1 引 言

海洋中的亚中尺度涡旋（半径10—50 km）对于海洋动力学和生物学研究有着重要意义（Lévy 等，2012），但是传统高度计存在覆盖范围小，重返时间长，观测精度低（Enjolras等，2006）等问题，使其仅能观测到6%—10%的涡旋（Amores等，2018），因此传统高度计很难满足对涡旋的观测要求（Chelton和Schlax，2003；Chavanne和 Klein，2010）。

为了解决这一问题，NASA、CNES、CSA合作提出一项预计于2022年发射的飞行任务（Durand等，2010；Gaultier等，2016a）：SWOT（Surface Water and Ocean Topography）任务。SWOT 搭载Ka 波段的宽刈幅干涉高度计，在两个扫描带上进行干涉测量，在间隙中使用Jason 级星下点高度计进行观测。为实现观测海洋上快速变化的亚中尺度过程（Morrow等，2019）的科学目标，SWOT的重复周期为20.86 d，子周期10 d，分辨率可达5 km。Fu 和Ubelmann（2014）从空间分辨率和覆盖范围等方面论证了宽刈幅高度计SWOT相比传统高度计对涡旋观测能力的提升，但Wang等（2019）说明SWOT的观测能力受纬度位置和季节因素影响，Ma 等（2020）也说明SWOT误差会影响6.5%的涡旋观测。

因此为了更精准地观测到更多的亚中尺度涡旋，要求对SWOT 平台仪器进行严格的误差控制，同时在数据层面建立误差估计方案，降低误差对亚中尺度海洋信号的影响。Gómez-Navarro等（2018）尝试利用滤波方法去除误差，但只能恢复40—60 km波长范围内的海洋信号，对于15 km 波长海洋信号的观测问题仍未解决。而Ubelmann 等（2018）利用交叉谱分析进行误差估计，虽然效果良好，但只能应用于CalVal 调试运行轨道，因此众多研究学者将误差解算重点放在SWOT与其他卫星的地理空间观测交叉区域上。

其实通过交叉区域估计误差的思想早在传统高度计误差估计中就有所应用，Faugere等（2006）就曾利用Envisat 与Jason 系列卫星的交叉点来评估Envisat 的观测能力，以及Ablain 等（2010）利用Jason-1与Jason-2交叉点来标定轨道误差。在SWOT误差估计方面，Pujol等（2012）就曾利用传统高度计来解算交叉区域SWOT 的测高误差。Dibarboure等（2012）根据基线误差具有距离向上呈现梯度变化的特性，提出了针对SWOT倾角误差和基线长度误差的交叉定标方法，可以将基线误差降低到厘米级，观测海洋亚中尺度信号的效果良好。Dibarboure 和Ubelmann（2014）对SWOT 分别在科学观测轨道（20.86 d 周期10 d 子周期）、应急轨道（20.86 d 周期1 d 子周期）和CalVal 轨道（1 d 重复周期）3 种轨道运行时，采用SWOT 自交叉以及外部星下点交叉对基线倾角误差进行估计，结果表明交叉定标在不同纬度上覆盖范围虽略有差异但有着良好的校准能力。Dibarboure 等（Dibarboure等，2012；Dibarboure 和Ubelmann，2014）对基线倾角误差进行误差估计，效果良好，减弱了基线倾角误差的影响，但对相位误差的估计仍未有很好的方法。

相位误差是两个干涉雷达信道之间的相位不平衡（Rosen 等，2000）反映到测高上的误差，如相对相位差1°对应在刈幅60 km 处的测高误差为16 cm，是误差估计的重点研究内容之一。其产生与不同的飞行系统和Karin 组件有关，Peral 和Esteban-Fernandez（2018）在SWOT 任务的误差预算文件中认为产生原因有3点：（1）由任何电子雷达子系统引入的两个干涉雷达信道之间的相位漂移；（2）由天线和机械/热子系统引入的相位漂移；（3）系统相位失配。虽然可通过设定仪器漂移速率要求，以及调整SWOT旋转太阳能电池序列等方法避免一部分相位误差的产生（Peral 和Esteban-Fernandez，2018），但当仪器的漂移速率达不到要求时，即相位匹配相差超过0.15°时，刈幅60 km处的测高误差已经超出误差预算。在仪器设定精度难以达到时，难以识别海表面高度差异较小的区域内的中尺度特征，此种情况下对相位误差进行估计是十分必要的。

根据相位误差与倾角误差类似的特点，即在单侧刈幅上存在梯度变化（Metref 等，2019），基于Dibarboure 等（Dibarboure 等，2012；Dibarboure和Ubelmann，2014）的文章中提到的交叉定标方法，本文提出了双侧刈幅独立交叉定标的方法。该方法将交叉定标方法扩展应用于相位误差和基线倾角误差的复合误差估计中，扩充交叉定标方法的适用范围，以期对多种误差复合输入的情况进行整体误差估计。

2 误差特性与交叉定标方法

2.1 基线倾角误差

基线倾角误差（Roll error，下均简称倾角误差）是由于卫星观测过程中干涉陀螺仪的抖动基线倾角发生不规则变化，角度测量仪器的精度有限，导致角度测量不准确，出现图1（a）中的δθ角的偏差，使得观测点的测高会出现δh的偏差。对于任何给定的时间点，确定了方位向位置al和距离向位置ac即确定了倾角误差hθ(al, ac)，公式表示如下（Gaultier等，2016b）：

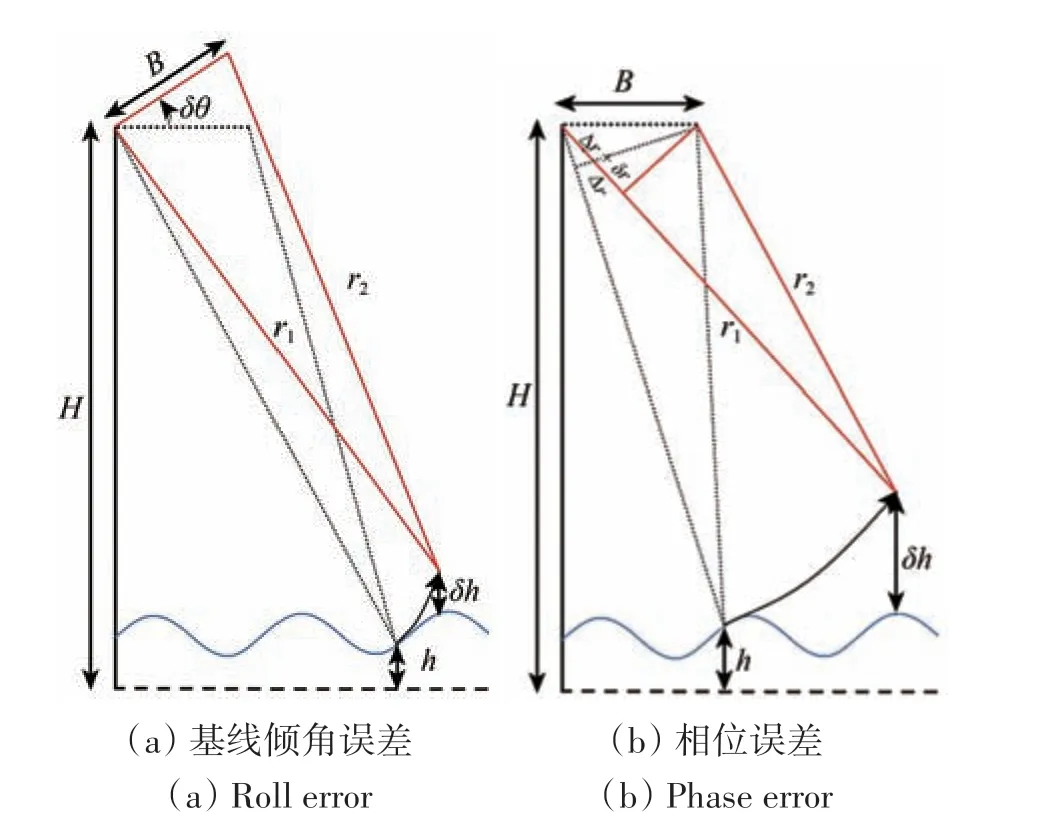
图1 误差形成示意图Fig. 1 Error formation

式中，ac为观测点距星下点距离xac（即距离向上的距离，下式（2）同），RE为地球半径（下式（2）同），H是卫星距大地水准面的高度（下式（2）同），θroll（al）为倾角的变化量，仅与方位向位置al相关。因此同一时刻左右刈幅倾角误差与距离向上距星下点离的平均斜率（本文所指平均斜率是同一时刻误差除以观测点距星下点距离的平均值，用p（t）表示，下文所有梯度/斜率）是一致的。即如图2（a）所示，左侧为采样数据中的倾角误差，选取特定距离向数据，如黑色实线，其对应的误差分布如右图所示，xac与Roll error成线性关系，即连线表现为一条过原点的直线。

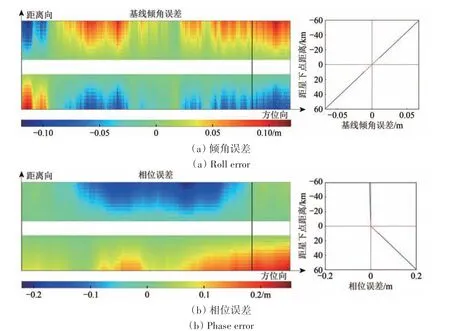
图2 误差特点示意图Fig. 2 Error characteristic

2.2 相位误差

相位误差（Phase error）是干涉对中的两个信号路径之间的相对相位的变化反映到海平面的测高误差。对于任何给定的时间点，确定了方位向位置al和距离向位置ac即确定了相位误差hθ（al，ac），公式表示如下（Gaultier等，2016b）。

式中，B是基线长度，KKa是指Ka波段的波数，（al）是方位向上的相对相位变化，仅与方位向位置al相关。由于同一时刻左右刈幅的相位变化不相关，相位误差在左右刈幅上分别与距离向上距星下点距离xac呈线性关系，且左右刈幅的斜率不同。即如图2（b）所示，左侧为采样数据中的相位误差，选取特定距离向数据，如黑色实线，则其对应的误差分布如2（b）右图所示，单侧刈幅上xac与Phase error成线性关系，即连线表现为一条过原点的直线。因此可以分左右刈幅类比倾角误差，通过交叉定标方法进行解算。

2.3 交叉定标方法及原理

卫星在绕地观测中相隔一段时间（小于周期）内会重访一段区域，利用两轨刈幅的观测值相减将海洋信号与测高误差剥离，再通过计算两轨的误差值，再通过观测值减误差值来估算海洋真值，即为交叉定标（Dibarboure等，2012）。

在观测中，由于卫星的轨道信息已知，观测点经纬度坐标（lon，lat）可通过轨道数据换算为距星下点距离xac（即距离向上距星下点的距离，下同）和时间t的函数，所以下文中观测点的观测值都以Hobs（xac，t）表示。

观测值Hobs由真值Hreal和含有距离向梯度的误差Errorgradient（xac，t），以及其余误差去除后的残差ε构成（下式（5）同）。其中距离向上具有梯度变化的误差值Errorgradient（xac，t）可以表示为

p（t）为随时间变化的量，对于Roll error误差来说，左右刈幅上的p（t）在同一时刻具有唯一值；而对于Phase error来说，左右刈幅上的p（t）不是一定相同的，即同一时刻左刈幅的p1（t）具有唯一值，右刈幅的p2（t）同样具有唯一值，但二者一般不同，符号可能相同，也可能相反，绝对值上一般也差距较大。

如图3（a）所示，当相隔一段时间后，第二轨刈幅经过第一轨刈幅的区域，即有部分观测点像素重叠时，对于第一轨来说重叠区域的时间节点为t0和t1，通过将两轨刈幅交叉区域（即图3 中深灰色菱形块）的观测值之差Y在公式中消去Hreal，通过两条刈幅之间具有距离向梯度的误差差异，来计算出t0—t1时间段的误差梯度值p（t）的变化，反算出t0—t1的误差值，进而估算海表面高度值（Dibarboure等，2012）。在两个刈幅交叉的菱形区域内，任一点的观测值之差可以写作Y（lon，lat，t），其模型中主要成分满足式（5），其中δH为重叠区域（图3中深灰色菱形块）模型值之差，对应于两次观测之间的海洋变化。

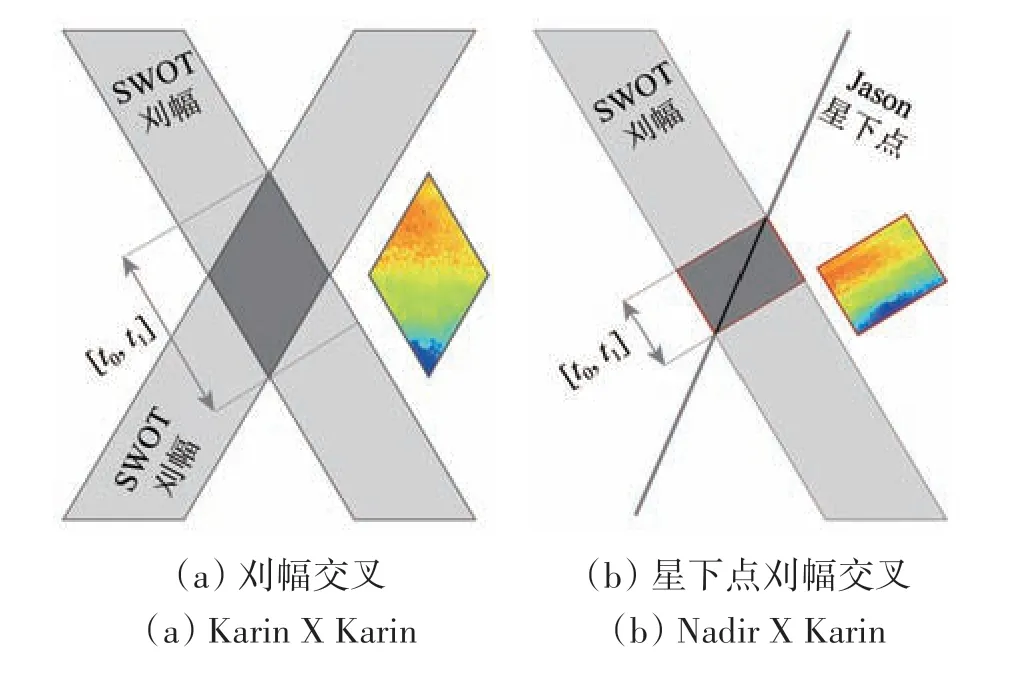
图3 交叉定标示意图Fig. 3 Schematic diagram of cross calibration

如图3（b）所示，星下点刈幅交叉的核心思想是通过星下点在刈幅上交点对应的起始时刻t0和结束时刻t1来提取刈幅观测值，再将对应的星下点观测值插值到刈幅数据的网格上，用插值后的星下点观测值Hnadir与图中红框矩形块内Hobs作差在公式中消去Hreal，进而估算海洋信号观测值（Dibarboure 等，2012）。星下点与刈幅交叉过程中，由于星下点观测值不含基线倾角误差和相位误差，而星下点自身误差在2 cm 左右，则有式（6），其中δH为重叠区域（图3 中深灰色矩形块）模型值之差，对应于两次观测之间的海表面高度变化，ε为其余误差去除后的残差以及星下点数据误差。

利用矩阵M表示xac，矩阵P表示p（t），则可简化成式（7）进行求解，列出观测点距轨道星下点的距离矩阵M以及观测点观测值的差值（即图3中深灰色菱形块的观测值之差）矩阵Y，通过矩阵计算得到P，即可求得对应于两轨道对应时刻位置的不同斜率值p（t）、p（t′）等，进而反算误差值。

由于相交叉两轨的时间相隔较短，交叉区域的海平面高度变化δH（lon，lat，t-t′）较小（HYCOM数据日变化差值为3 cm 左右，在实际计算中交叉区域海表面高度变化差值更小），低于交叉定标误差解算的最低极限值。

3 数据结果处理与分析

实验所用刈幅采样数据是基于Gaultier 等（2016b）研发的工具SWOT Simulator模拟生成。数据源是采用HYCOM（Hybrid Coordinate Ocean Model）2015 年 的SSH （Sea Surface Height） 数 据，采 用SWOT科学卫星轨道，轨道高度为891 km，周期为20.86 d，分辨率取5 km，本实验数据时间跨度为25 d（注，时间跨度指第一轨与最后一轨的时间差在25 d 左右），使单个周期内首轨和末轨都得到充分交叉观测，以保证第3 天至第23 天该区域内的重叠观测数据满足一个完整周期。实验所选区域经度从180°向东到80°W，纬度从67°S 到0°，包括了南太平洋东部的大部分地区。该区域主要的特点是区域内岛屿及陆地较少，而海洋范围较大，足够获得连续的多组采样数据。纬度选择主要是由SWOT卫星的覆盖范围以及交叉区域的数量来决定。根据SWOT 的轨道方案，3 天内其刈幅自交叉的区域主要分布于中纬度地区，在赤道附近无重复观测。

实验中所用星下点数据是基于SWOT Simulator模拟工具。数据源采用HYCOM 2015 年的SSH 数据，Jason-2卫星科学轨道参数（2016年10月前轨道，2016 年发射的Jason-3 与其轨道参数相同）来源于Aviso 官网（轨道高度为1336 km，周期为9.9156 d），分辨率取5 km。由于星下点数据误差整体在2 cm 以内，但实验中交叉定标的误差处理中部分可低至2 cm，所以本实验也将星下点数据误差作为背景误差纳入实验中。

SWOT Simulator生成的沿轨采样数据要进行网格化处理转换成经纬度坐标系，进而提取出两条沿轨采样数据在海表面的交叉区域。交叉定标的实验方案基于前文研究进行设计，由于Phase error同一时刻左右刈幅的p（t）不同，所以在网格化采样数据的过程中将同一轨的左右刈幅数据分开，分别生成两个网格文件，在后续的交叉定标环节中视作两个沿轨采样来进行定标。实验中对于单独一个刈幅来说，虽然同一时刻只计算出一个P（t），但该值实际上是基线倾角误差Proll（t）和相位误差Pphase（t）的和。误差反演主要目的是为了将误差去除，所以并未深究基线倾角误差或相位误差各自的大小，而是将其视为一个整体考虑，意在降低复合误差对海洋信号观测的影响。

实验中，并不是所有的交叉观测都可以进行交叉定标，Dibarboure等（Dibarboure等，2012；Dibarboure和Ubelmann，2014）的研究指出，两条刈幅相隔时间为1—3 d 时可以进行交叉定标；但由于本文所选区域（180°—80°W，67°S—0°的南太平洋东部地区）海表面高度变化剧烈，本文统计了2015 年HYCOM 相邻1 d 的海表面高度变化（绝对值），平均约为2 cm，而相邻2—3 d平均约为3.8 cm，此时海表面高度变化被误认为测高误差进行校正的比例增大，造成亚中尺度信号的泄露增多。因此，为降低两个交叉刈幅的相隔时间对定标结果的影响，在筛选刈幅时，限定相隔时间为1 d。

而且，交叉定标计算对交叉区域的大小有一定的要求，对较小的区域内进行误差估计往往呈现处较大的异常值，因此对交叉区域观测点个数进行了一定的筛选。在星下点刈幅交叉实验中，由于星下点本身数据较少，交叉区域观测点个数有限，因而并未对观测点个数进行定量筛选。

3.1 SWOT刈幅自交叉定标

SWOT 刈幅自交叉定标是基于式（5）、（7），利用相隔一天时间内的重访同一地区的两轨采样数据，通过式（5）和式（7）中的矩阵计算，得到估计的p（t）值，接着乘以该观测点距两轨星下点距离来反算测高误差值，再用观测值减去估算的误差值得到处理后的结果值。由于相位误差存在，左右刈幅的整体误差值并不具有明显相关关系，实验中将双侧刈幅独立交叉计算，在批量统计时也不考虑左右刈幅，仅将任意两条单侧刈幅的交叉区域视作一个交叉点，约是以往交叉定标区域面积的四分之一。本实验从误差分布区间、交叉区域的误差绝对值的平均值和误差的标准差3个方面综合评估。

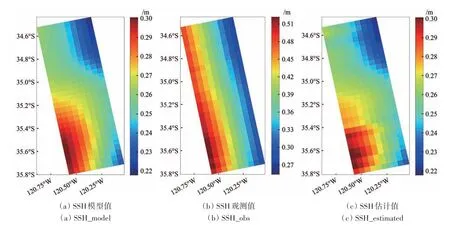
实验样例1中，当海洋信号与误差相近时，从图4（b）可见误差掩盖了图4（a）中的海洋信号（图4（b）中海表面高度值为30—50 cm），经过交叉解算，20 cm 的误差值降低到可接受的2 cm 以内，在结果图4（c）很好的还原出4（a）中海洋信号的分布特征，误差处理效果良好；实验样例2中，图5（b）中误差削弱了图5（a）中的海洋信号，经过交叉解算后，很好地还原出海洋信号特征，误差残差值（图5（f））已经降到可接受的1 cm以内，误差处理效果良好。

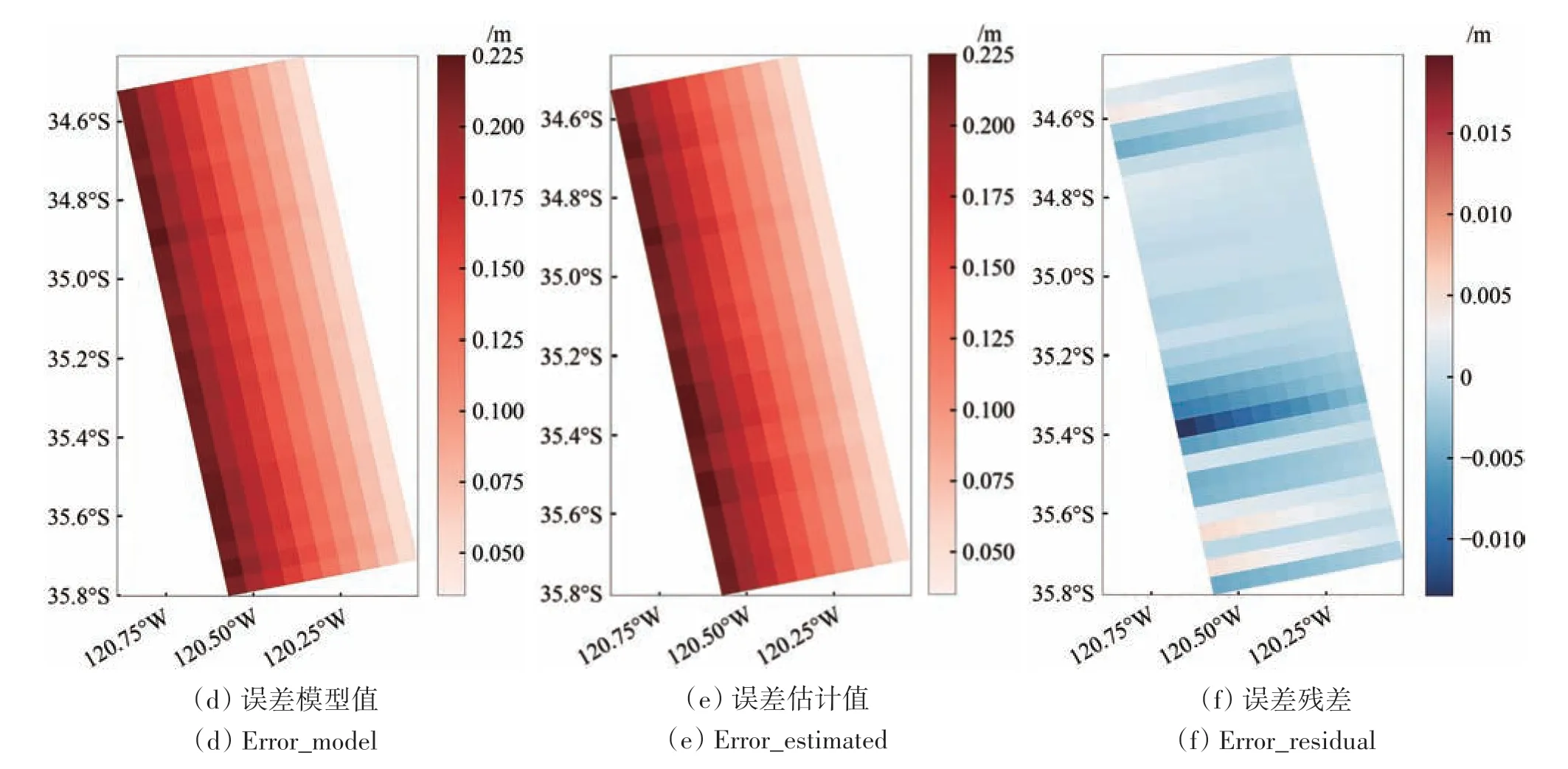
图4 交叉定标前后对比图（样例1）Fig. 4 Example of swath before and after cross calibration （example 1）

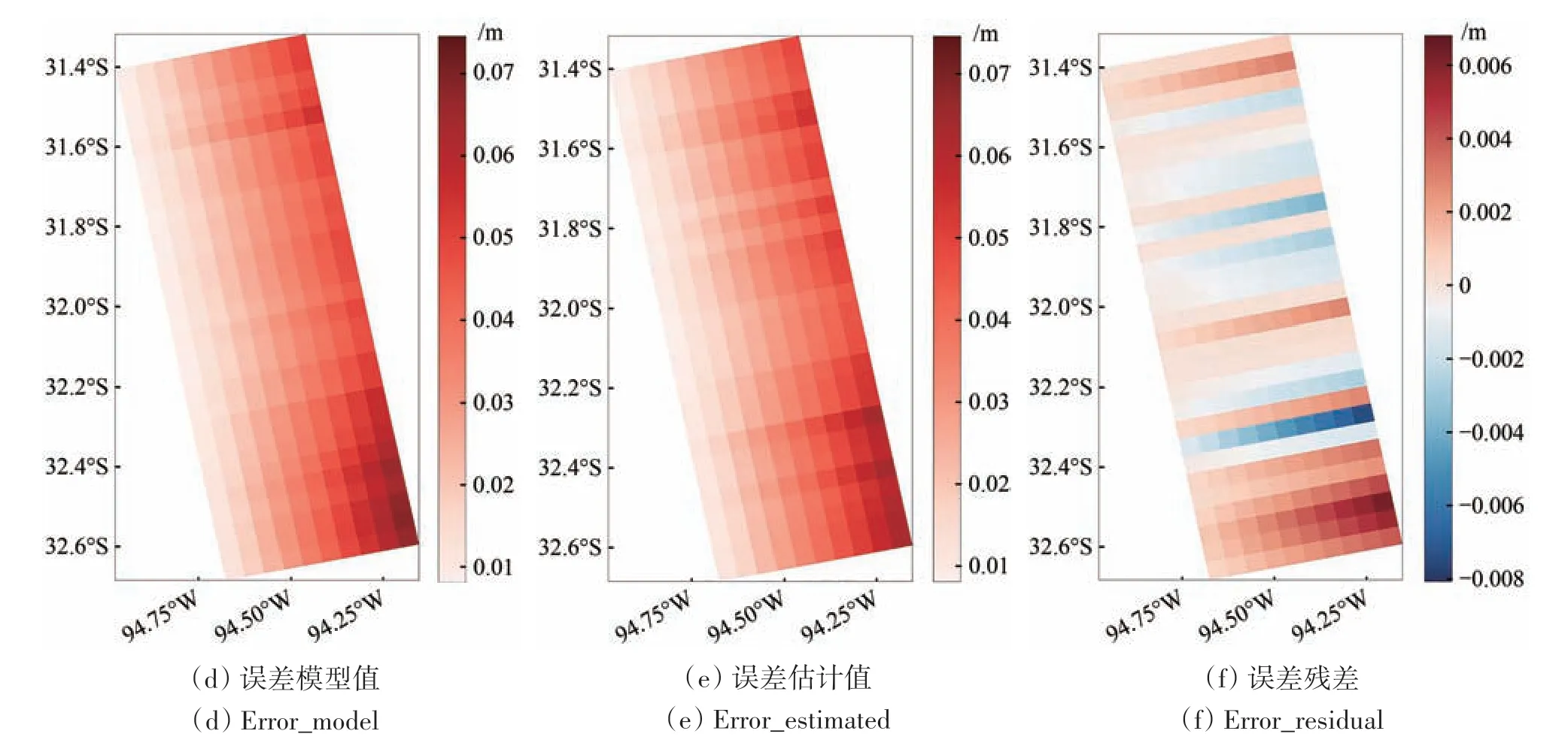
图5 交叉定标前后对比图（样例2）Fig. 5 Example of swath before and after cross calibration （example 2）

从以上两组样例中可以看出，无论海洋信号与测高误差相近或相差较大，交叉定标方法通过将两组观测值作差，都有效降低了海洋真值在误差处理中的影响，仅保留两轨采样数据中的误差差值再进行计算，增大了误差值在计算值中的权重，从而较好的进行误差反演。为了更直观更准确的评估刈幅自交叉的效果，对一个周期内的批量刈幅交叉定标结果进行统计，从上文提到的3个方面综合评估。

本次刈幅自交叉实验中共有2938个交叉区域，观测值共553246个，从图6（颜色表示核密度估计（KDE）计算的数据密度，黑线为对角线）可见，误差在10 cm 内分布集中，且误差模型值—误差估计值呈梭形分布于对角线附近，反映出刈幅交叉解算出的误差值和模型值较为接近。从图7 可见，解算前，误差平均值在2 cm 内的占比为16%，解算后占近77%，提升近4倍；解算前，误差标准差在2 cm 内占比为34%，解算后占近73%，提升一倍多。所以从平均值和标准差看，SWOT刈幅自交叉方法对交叉点的误差反演效果良好。

图6 误差模型值—误差估计值的散点分布图Fig. 6 Scattered density diagram of Error_model-Error_estimated

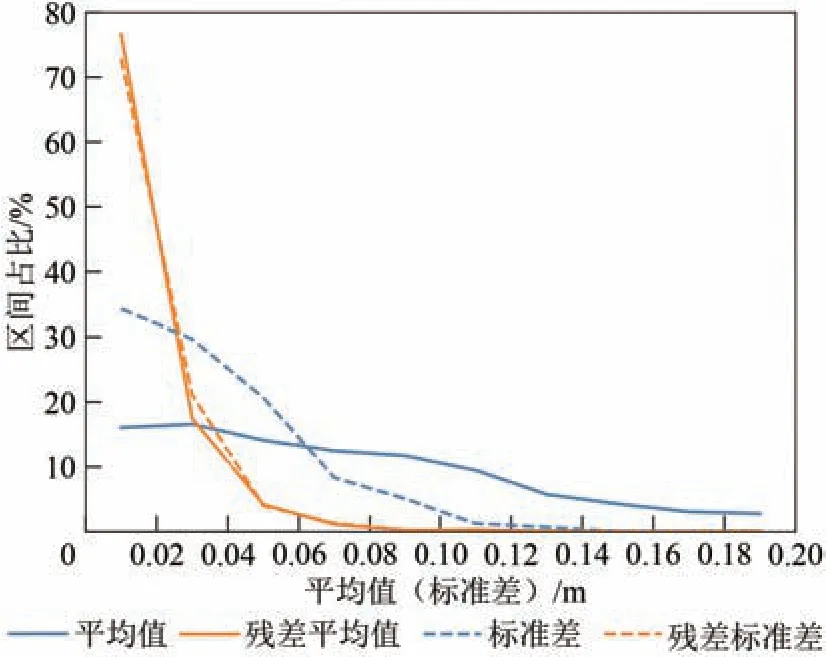
图7 误差绝对值的平均值与标准差的区间分布Fig. 7 Interval distribution of mean of absolute value and standard deviation of error value before and after Karin-Karin cross calibration

3.2 Jason星下点与SWOT刈幅交叉定标

Jason 星下点与SWOT 刈幅交叉定标是基于式（6）、（7），利用相隔一天时间内的重访同一地区的两轨采样数据，通过式（6）和式（7）中的矩阵计算，得到估计的p（t）值，接着乘上该观测点距星下点距离反算测高误差值，再用观测值减去估算的误差值得到处理后的结果值。与SWOT刈幅自交叉定标相同，采用双侧刈幅独立解算误差，并将误差残差分布区间、误差绝对值的平均值和标准差纳入结果统计。

Jason-2星下点—刈幅交叉实验样例1中，误差值与海洋信号较为接近，将海表面高度整体提高了近20 cm，且掩盖了海表面高度原本的分布特征，经过误差解算反演后，很好地还原出图8（a）中方位向上海表面高度分布差异，将误差降到可接受的2 cm以内，误差处理效果良好；实验样例2中误差值较小，但也影响了对海表面高度分布特征的识别，经过误差解算反演后，很好的还原出图9（a）中方位向上海表面高度分布差异，将大部分误差降到可接受的2 cm以内，误差处理效果良好。

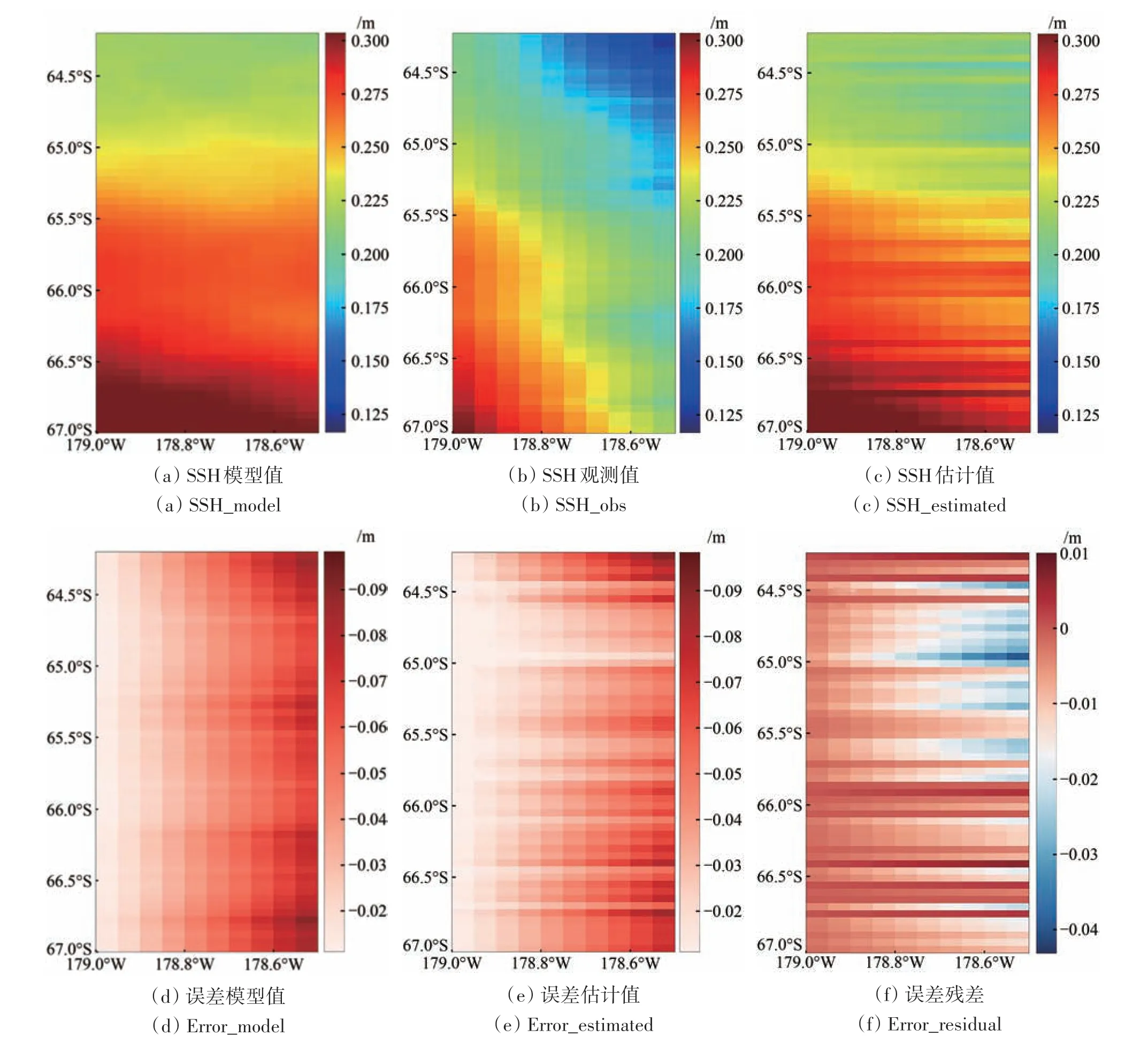
图9 星下点刈幅交叉样例2Fig. 9 Example of swath before and after nadir-Karin cross calibration （example 2）

从以上两组样例中可以看出，无论海表面高度值与测高误差量级相近或相差较大，利用Jason-2星下点来解算SWOT刈幅的误差效果良好，通过观测值作差增大了误差值在计算值中的权重，从而较好的进行误差反演。为了更准确的评估刈幅交叉的效果，对一个周期内的批量刈幅交叉定标结果进行统计，从刈幅自交叉部分提到的3个方面进行综合评估。

由图10（图10中颜色表示核密度估计（KDE）计算的数据密度，黑线为对角线）可见交叉定标后，在3373组交叉点中，误差在10 cm内分布集中，且误差模型值—误差估计值呈梭形分布于对角线附近，反映出星下点刈幅交叉解算出的误差值和模型值较为接近。输入的星下点误差约为2 cm，因此探究误差平均值分布时考虑4 cm内的分布情况，从图11可见，解算前，误差平均值在4 cm内的占比为33.4%，解算后占近87.7%，提升1.5倍多；解算前，误差标准差在2 cm内占比为36%，解算后占54.5%。所以，从平均值和标准差看，结合Jason-2星下点的SWOT刈幅交叉方法，对交叉点的误差反演良好效果明显。

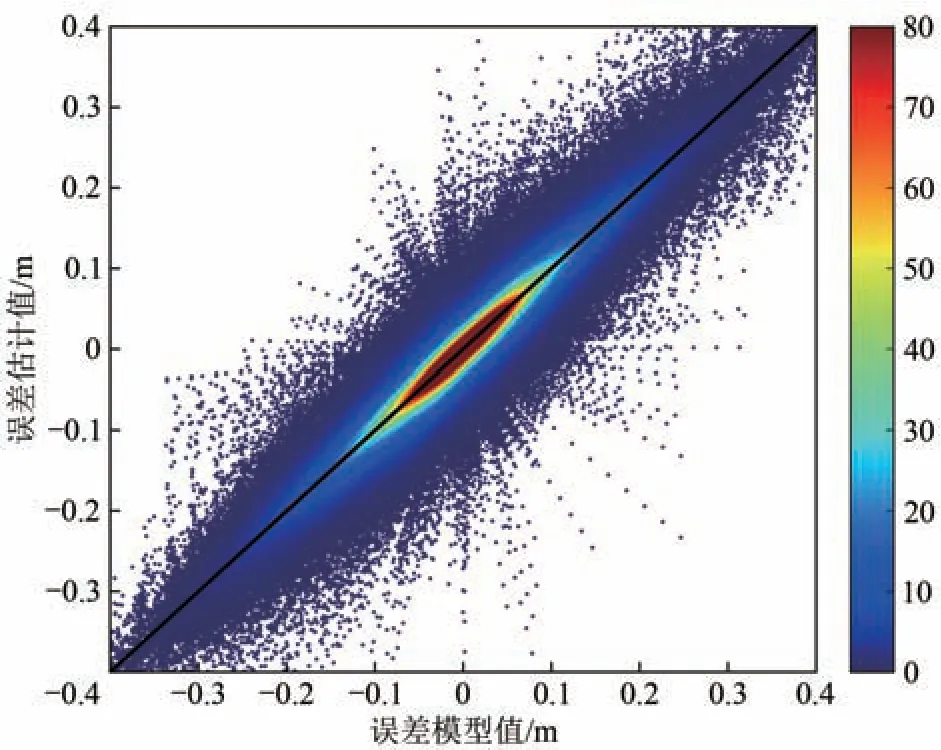
图10 误差模型值—误差估计值的散点分布图Fig. 10 Scattered density diagram of Error_model-Error_estimated

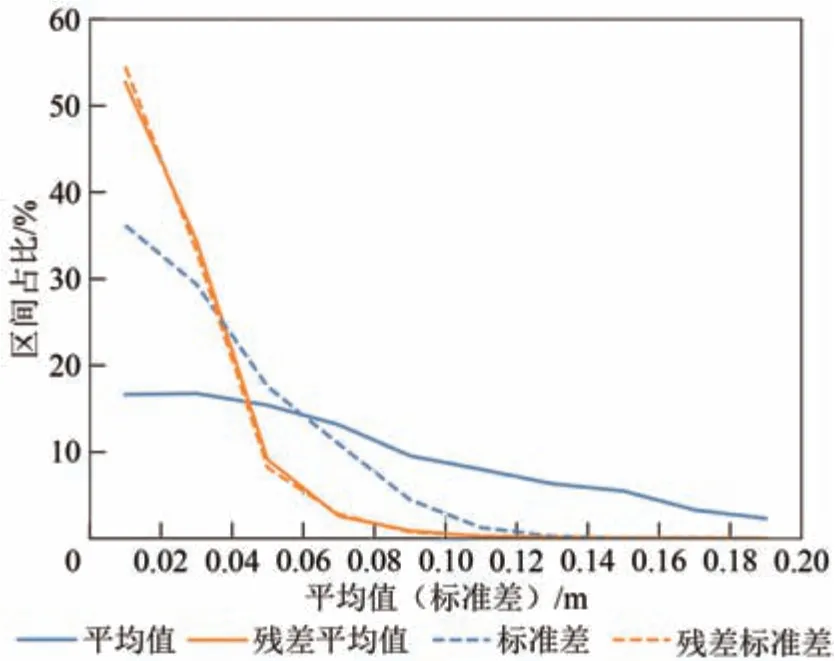
图11 误差平均值/标准差的区间分布Fig. 11 Interval distribution of mean of absolute value and standard deviation of error value before and after nadir-Karin cross calibration

3.3 结果分析与讨论

（1）交叉定标方法通过观测值相减的方式相当于削弱了海洋信号对误差处理的影响，将大部分的海洋高度模型值屏蔽，将误差保留，通过建立矩阵计算，进而估计误差来达到去除误差的效果。刈幅自交叉实验中从误差残差分布区间上看，本次实验中交叉点有2938个，观测值共有553246个，交叉定标解算误差前，误差真值在±0.50 m 内均有分布，解算后的残差在±0.10 m 外分布明显少于误差真值，绝对值在0—4 cm 内占比超过91%，0—2 cm 内占80%，比解算前提升一倍多，说明从误差残差分布区间上看SWOT刈幅自交叉定标对交叉点的误差解算良好；从平均值和标准差上看，交叉定标误差解算前后对比，0—4 cm 内的占比可达94%，0—2 cm 内的占比分别提升了四倍和一倍，反映出刈幅自交叉对误差反演效果良好，有效还原了海洋信号的分布特征。

无论是从误差残差或是平均值标准差的区间分布来看，对于单个交叉点来说，本方法将误差估计的较为准确，误差残差相比误差值降低到一个量级；批量实验中，交叉定标能将80%左右误差降到2 cm 以内，70%以上交叉点平均值标准差降到2 cm以内，说明刈幅自交叉方法有效。

（2）本次实验中SSH 数据来源于HYCOM 数据，通过模拟得到SSH 模型值，由于HYCOM 本身的时间分辨率限制，一天的全球海表面高度变化未能得到体现。这也导致相邻两天的采样数据中，即便相隔时间较短，但SSH 模型值的差距也很大。这种情况在此次实验的交叉定标中较为常见，而且没有很好的处理方法。模型值之间的差距一旦呈现出距离向的梯度就会被误认为相位误差或基线倾角误差被抹平，对实验结果造成了一定不良的影响；同样对于两轨均在同一天的数据来说，两轨的SSH 模型值是相同的，两者作差仅剩误差，有效提高了实验效果。针对这种基础数据的时间分辨率以及数据模拟方法的限制对实验效果造成的影响，暂时没有很好的解决办法。

（3）双侧刈幅独立交叉定标的方案是基于相位误差的分布特征提出的，即相位误差距离向斜率不一致。刈幅分开降低了每个交叉点的观测点数量，虽然对于单个交叉点来说观测点数量的减少对于误差估计是一个不利因素，但是通过实验结果来看仍能满足对大部分相位误差和基线倾角误差的整体解算要求。

（4）通过SWOT 刈幅自交叉实验以及Jason 星下点与SWOT 刈幅交叉实验结果对比来看，SWOT刈幅自交叉的交叉点区域数量不及星下点刈幅交叉。从误差和交叉点误差绝对值的平均值和标准差区间分布来看，刈幅自交叉将占比更高的误差残差降到了4 cm 内，结果呈现刈幅自交叉比星下点刈幅交叉效果好。从公式来看刈幅交叉中一次需要估算出两轨的p（t），而星下点刈幅交叉仅需估算单轨的p（t），从公式中的未知数来看，星下点刈幅交叉的未知数更少，估算应该更容易。但实际上，交叉定标误差反演效果差异关键在于交叉点的观测值个数上，刈幅交叉中一个交叉点的观测值个数至少为80个，而对于星下点刈幅交叉来说，由于星下点是单轨观测值，一个交叉点的观测值个数较少，一般在20 个值以内，星下点刈幅交叉是将星下点插值到刈幅的网格上，本身交叉点观测值少，加上插值过程中的不准确以及星下点误差的存在，综合影响了两种交叉方法的不同效果。

（5）本次实验误差输入时，未将误差高频变化去除。卫星经过每个交叉点的时间较短，对于星下点刈幅交叉区域仅为20 s 左右。当忽略高频抖动后，可以忽略交叉点区域内p（t）随时间的变化，可将单轨数据一个交叉点处单侧刈幅认定为一个p（t）进行误差估算。相应的刈幅交叉批量实验结果如下表所示，刈幅自交叉中将90%的误差降到4 cm 内，简化刈幅自交叉将97%的误差降到2 cm 内，星下点刈幅交叉将85.7%的误差降到4 cm 内，简化星下点刈幅交叉方法将近93%的误差降到4 cm 内；从平均值和标准差来看，刈幅自交叉中将2 cm 以内的平均值提升四倍多、标准差占比提升一倍，星下点刈幅交叉标准差2 cm 内占比从36.2%提高到54.5%，星下点刈幅交叉简化方法标准差0—2 cm 内占比已达94%，说明简化方法能够提高误差4 cm 内的百分比以及将94%以上标准差缩小到2 cm 内。这种简化方法是将交叉点处认定为单个p（t），本质上是估计了交叉区域内方位向上的误差平均水平，估计了较短时间内占有较大比重的误差低频变化，基于SWOT团队目前的误差仿真效果较好。而当误差仿真过程中高频信号占比更高时，前文提到的方法体现了误差在方位向上的变化规律，更适用。

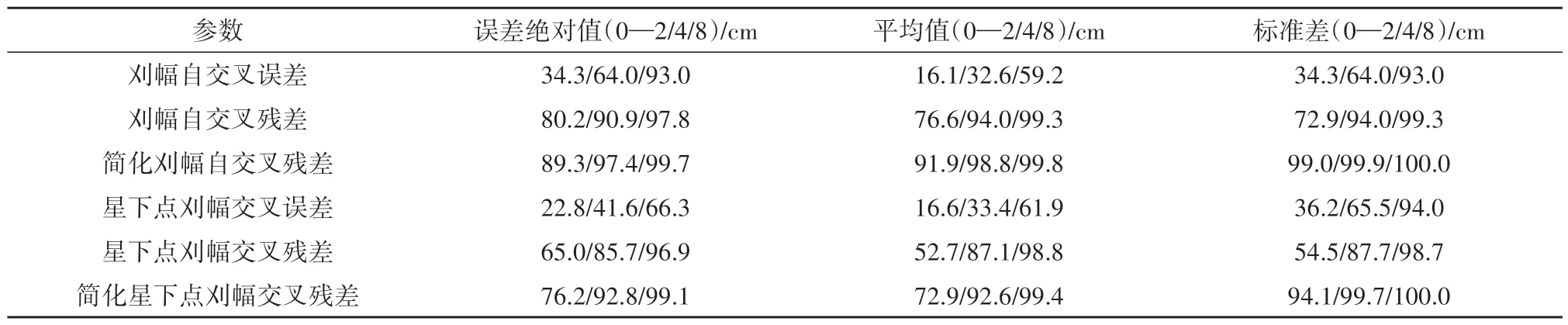
表1 误差和残差的区间分布Table 1 Interval distribution of errors and residuals/%

4 结 论

本文利用左右刈幅分别交叉定标的方法对基线倾角误差和相位误差复合输入的刈幅进行误差估计。其中由于单个交叉点的观测值个数差异，SWOT刈幅自交叉的误差解算效果比Jason-2 星下点刈幅交叉的效果好，但都有效提高了误差在0—2 cm 内中所占比例，以及平均值和标准差在0—2 cm 内所占比例，经过交叉定标解算误差后，80%的误差在4 cm 内。原因在于通过交叉的方式削弱了较大部分的海洋信号的影响，提高了计算过程中误差所占权重，再通过矩阵解算误差。针对相位误差不同于基线倾角误差的特点，即在左右刈幅距离向上的p（t）不同，故双侧刈幅独立交叉定标，计算出单侧刈幅距离向上的p（t），由于相位误差和基线倾角误差一同叠加在单侧刈幅上，所以计算出的p（t）直接反算即可估整体误差。综上，实验结果表明在仪器精度较低的情况下，双侧刈幅独立交叉校准的方案能够科学有效地估计两种误差的复合输入值，显著降低了误差水平。

本次实验也反映出只要误差在距离向上呈现梯度变化规律，都可通过交叉定标方法利用矩阵解算出误差值，进而降低误差对观测的影响；同时当误差产生原因不同但具有共同特点时，即同样与距离向上距星下点距离成正比或是满足其他的关系，可以将具有固定值的参数简化成一个常数，统一式子将误差表示成距离向上距星下点距离的一次项（或多次项）与斜率乘积的形式进行表达，不需要将两种误差彼此分开，将两种误差统一进行解算，即可反演出整体误差，这种方法将有助于解决多种误差混合的情况下的误差处理。基线长度误差也是测高误差中重要成分之一，由于基线长度误差在距离向上分布与相位误差、倾角误差不同，结合基线长度误差的误差进行交叉定标仍有待进一步研究。

在之后的研究中，如能提高采样数据的时间分辨率改进模拟工具使采样数据能反映出一天内海洋表面的动态变化，更接近海洋的真实情况，则能进一步提高交叉定标误差解算能力，提升反演效果；另外，交叉点数量对误差解算的影响则需要更进一步的研究。