北极海域SAR海浪方向谱反演及其与中法海洋卫星CFOSAT/SWIM 数据的比较

黄冰清， 李晓明， 蔡琼琼

1. 中国科学院空天信息创新研究院 数字地球重点实验室, 北京 100094;2. 中国科学院大学, 北京 100049;3. 国家海洋环境预报中心, 北京 100081

1 引 言

北极是全球气候变化的敏感区域，其变暖速度约是全球平均水平的两倍，该效应被称为“北极放大效应”（Serreze 和Francis，2006；赵进平 等，2015）。在全球升温的背景下，北极海冰持续减退，北极地区的反照率降低使地表吸收更多太阳辐射，进而加速了海冰的减退，形成了北极放大的正反馈效应（Serreze 和Francis，2006；赵进平 等，2015）。近年来，卫星资料显示北极海域风场存在增强趋势，同时，伴随着海冰的持续减退，北极海域的固有风区增大，新风区产生，在这些因素共同作用下，海浪进一步成长（Thomson 和Rogers，2014；Liu 等，2016）。增强的海浪向海冰内部传播，与海冰发生相互作用，导致海冰破碎、消融，可能进一步引起海冰的持续减退（Kohout等，2014）。然而，由于北极地区观测数据的缺乏，对于这一过程的认知是当前研究的薄弱环节（Kohout 等，2014）。此外，伴随着北极季节性海冰的减退，北极航道的开通和利用极大节约了航运成本，但同时风险并存。航道上准确的海况监测也是船只通航安全保障的重要内容。

目前北极海冰—海浪相互作用的研究多利用有限的现场观测数据以及模式模拟结果。然而，由于北极地区的特殊地理环境及气候条件，浮标观测、随船测量等传统观测手段很难在大范围内获取持续的观测数据。雷达高度计RA （Radar Altimeter）和合成孔径雷达SAR（Synthetic Aperture Radar）等具有全天候、全天时工作优势的微波传感器成为了北极海况持续观测的有效技术手段。卫星雷达高度计主要侧重海表波高的测量，而星载SAR 则能够提供海表的二维信息，更全面的描述海浪特征。除星载SAR 以外，2018 年发射的中法海洋卫星CFOSAT（China-France Oceanography SATellite）上搭载的波谱仪SWIM（Surface Wave Investigation and Monitoring）作为一种实孔径雷达，也能够提供海浪二维信息。然而由于缺少实测的二维谱数据，SWIM 谱数据的对比验证较为困难。尽管部分浮标数据可提供二维的海浪谱信息，但多数浮标提供的方向谱数据并非严格意义的海浪方向谱，而是通过频谱和方向分布函数计算得到（Earle 等，1999）。因此SAR 反演的海浪方向谱数据也是SWIM谱产品的重要验证数据集。

欧洲航天局于2014 年和2016 年相继发射了哨兵1A（S1A）和哨兵1B（S1B）卫星，这两颗双子星可在2 天内实现对北极地区的完全覆盖。哨兵1号的干涉宽幅IW（Interferometric Wide Swath）模式是其在北极地区的主要成像模式之一，提供了幅宽约250 km，分辨率为10 m 的高分辨率SAR 影像数据（ESA，2013），为北极海域海浪的监测积累了良好数据基础。尽管SAR 具有高分辨率二维成像的突出优势，但由于SAR 对海浪的成像过程是一个复杂的非线性过程，存在方位向高频信息截止和传播方向模糊的问题（Alpers 和Rufenach，1979；Hasselmann 等，1985），因此从SAR 图像中反演海浪信息较为困难。缺少如雷达高度计一样成熟的海浪遥感数据产品限制了星载SAR 数据在海浪研究中的广泛应用。本文期望通过实验数据验证传统方法和在轨的卫星SAR 数据在北极海域海况监测反演的适用性和可行性，促进SAR 数据在北极海域海况监测及相关研究中的应用。同时为SWIM 波谱仪谱数据产品的对比验证提供可靠的数据集。

目前，已有的海浪信息反演方法可大致分为4 类：（1）非线性算法。Hasselmann 等在推导了海浪方向谱到SAR 图像谱的非线性变换关系基础上，提出了经典的MPI海浪方向谱反演算法（Hasselmann和Hasselmann，1991；Hasselmann 等，1996）。该方法通过引入外部先验信息来确定海浪传播方向并弥补丢失的高频海浪信息，进而反演获得完整海浪方向谱。此后，基于非线性变换关系，国内外研究学者又相继发展得到了参数化和半参数化等反演算法（何宜军，1999；Mastenbroek 和De Valk，2000；孙健，2005）。（2）准线性的交叉谱反演算法（Engen 和Johnsen，1995）。该算法是欧洲航天局海浪谱二级产品的标准算法，但该算法将非线性关系降级为准线性关系，仅能获得截止波数内的涌浪谱，且在高海况下误差较大（王贺 等，2008；Li等，2010）；（3）参数化经验模型算法，如CWAVE 系列参数化模型算法（Schulz-Stellenfleth 等， 2007； Li 等， 2011； Stopa 和Mouche，2017），通过建立SAR 图像特征与海况参数之间的关系，从而反演获得全海况的海浪参数信息，具有良好的业务化应用前景。目前基于该方法已形成一套年代际的全球海浪SAR 遥感数据集（Li和Huang，2020）；（4）机器学习方法也为解决海浪信息非线性反演问题提供了新的解决途径（Stopa 和Mouche，2017；Shao 等，2019；Wu 等，2021）。如Stopa、Wu 等与将传统经验算法所采用的参数与机器学习非线性映射能力相结合，可以更准确地反演获得海浪特征参数，例如有效波高。在上述方法中，非线性反演方法，如MPI 算法，是反演获得完整海浪方向谱数据常用方法（Heimbach 等，1996；王来部和冯倩，2004；刘晓燕 等，2017；黄冰清 等，2017）。海浪方向谱相比一维海浪参数能够全面反映海浪的组成、能量分布、传播方向等信息，尤其在海浪向冰传播能量衰减过程研究中能够发挥突出优势，可揭示不同频率的海浪衰减过程以及波向的变化过程。因此，为了后续开展北极边缘海海浪与海冰相互作用研究，本研究重点开展基于S1 宽幅SAR 数据的北极海域海浪方向谱的反演研究。

基于北极地区获取的高分辨率S1 SAR 影像数据，本文将开展北极海域海浪方向谱的反演及其与SWIM 波谱仪测量结果的比较研究。一方面，将为SWIM 波谱仪的二维谱数据产品提供良好的海浪方向谱验证数据集，另一方面也将为北极边缘区海浪与海冰相互作用研究奠定数据和方法基础。

2 数据及研究方法

2.1 数据

2.1.1 SAR数据

本文使用的SAR数据为欧洲航空局提供的S1A和S1B 的IW 模式数据。该模式是哨兵1 号在北极地区的主要成像模式之一，具有HH（Horizontal-Horizontal） 和HV （Horizontal-Vertical） 或VV（Vertical-Vertical） 和VH（Vertical-Horizontal） 两种极化组合方式。IW 模式数据的幅宽约250 km，空间分辨率为10 m（ESA，2013）。该模式每月在北极可获约2000 景数据，是北极地区海况持续监测的良好数据源。

图1 展示了本文的研究区域，主要包括格陵兰海及挪威海海域。此区域连接了北极海域与开阔的大西洋，容易观测到产生自北大西洋开阔水域并向海冰覆盖区域传播的海浪案例，因此选择该区域作为研究区域。在此研究区域内，本文共使用了在2020 年9 月的114 景IW 数据，包括91 景VV 极化和23 景HH 极化数据，其空间分布分别为图1中红色和蓝色方框所示。

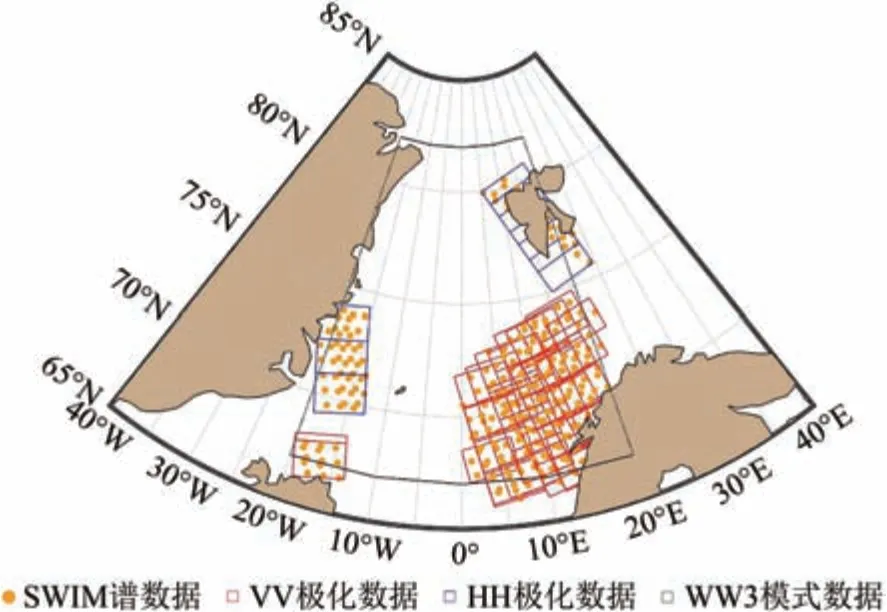
图1 2020年9月S1 IW数据（VV极化：红框；HH极化：蓝框）的分布，WW3模式数据获取区域（黑框）以及SWIM谱数据（橙色圆点）空间匹配情况Fig. 1 Map of the study area. The red and blue square denote the WW3-collocated S1 data in VV and HH polarization，respectively， in September 2020. The black box marks the region of WW3 model data. The orange dots mark the collocated SWIM spectrum data in the month

在进行反演前，本文参照了欧洲航天局的哨兵1号数据手册对SAR数据进行降噪和辐射定标预处理，公式表达如下（ESA，2013）：

式中，σ0为后向散射系数，DN 为SAR 图像的灰度值，n为影像的噪声矢量，ks为辐射定标常数。

2.1.2 WW3 模式海浪谱数据

MPI海浪方向谱反演算法需要借助外部先验信息。本文中使用了国家海洋环境预报中心全球海浪数值预报系统提供的预报产品作为先验信息。该预报系统基于全球第三代海浪数值预报模式WW3（Wave Watch III）（Tolman，1997，1999，2009）6.07版本，系统空间分辨率为0.1°。本研究中使用了该系统所输出的每日12 时至次日12 时的24 h 的海浪二维方向谱预报产品。数据覆盖区域如图1中黑框所示。输出的二维谱数据时空分辨率分别为1 h 和0.5°。二维谱的频率范围是0.04118—0.4056121 Hz，对应海浪波长范围约为9—920 m，整个频谱按对数平均分为25 个频率区段。二维谱的方向范围是0°— 360°，平均分为48个方向。

2.1.3 SWIM波谱仪数据

SWIM 是中法海洋卫星CFOSAT 上搭载的星载波谱仪，是一个工作于Ku 波段的实孔径雷达，具有6 个入射角（0°、2°、4°、6°、8°和10°）。数据获取范围可覆盖南北纬80°内的海域。在0°入射角下，SWIM 波谱仪工作模式类似于传统雷达高度计，可测量海浪的有效波高信息，测量足印宽度为18 km。在6°、8°和10°入射角下，SWIM 波谱仪测量获取海浪的斜率谱数据，方向角度分辨率为15°，谱数据的波数范围为0.0126—0.2789 m-1，对应波长范围约为23—500 m（Tison和Hauser，2018）。本文中使用的SWIM 波谱仪数据由法国国家空间局卫星海洋学存档数据中心（Aviso+）提供。已有的研究结果表明，SWIM 波谱仪在星下点测量的有效波高与Jason-3以及SARAL高度计测量结果十分接近，其偏差分别约为0.01 m 和0.06 m（Hauser 等，2021）。与法国气象局业务化运行的MFWAM 海浪模式数据结果对比显示，SWIM 在10°入射角波束下测量的谱数据较6°和8°入射角下测量结果具有更高精度，谱积分得到的有效波高偏差为0.02 m，均方根误差为0.26 m，谱的传播方向以及主峰波长的偏差分别为3.9°和-12.3 m，均方根误差为26°和33 m（Hauser 等，2021）。因此，本文采用10°入射角下的SWIM谱产品与SAR反演的海浪方向谱结果进行对比验证；此外亦采用星下点测量的有效波高数据对SAR 反演谱积分得到的有效波高参数进行对比验证。

SWIM 波谱仪在10°入射角下谱的覆盖范围约为70 km×90 km。图1 中橙色圆点即表示与SAR 反演结果匹配的该入射角波束下覆盖范围的中心经纬度。SWIM 测量得到的是斜率谱，反映了海浪波陡的分布情况。而海浪方向谱，即波高谱，则反映了海浪波高的分布，二者之间存在如下关系（Tison和Hauser，2018）：

式中，F(k，θ)表示海浪方向谱，E(k，θ)表示海浪斜率谱，k为波数，θ为海浪谱的方向。

SWIM 的二级产品中共提供了4 种星下点有效波高数据，本文中使用的是具有最高采样率的有效波高数据（nadir_swh_nsec，简称NSEC 有效波高数据）。NSEC有效波高数据由SWIM 星下点原始测量结果经编辑、平滑、平均等处理后得到，连续两个数据产品的时间间隔约为220 ms，空间间隔约为1.5 km。NSEC 有效波高数据数目与原始测量数据数目一致，提供了数据量更丰富的星下点有效波高测量结果，因此在本研究中用于S1 SAR反演的有效波高数据的比对。

2.2 MPI海浪方向谱反演方法

1991 年，Hasselmann 等推导得到了海浪方向谱到SAR 图像谱的非线性关系，并在此基础上提出了MPI 海浪方向谱反演算法（Hasselmann 和Hasselmann，1991；Hasselmann 等，1996）。MPI算法通过引入模式运行产生的海浪方向谱数据（称为第一猜测谱）来提供海浪传播的方向，并弥补丢失的高频信息。该算法在迭代运算中不断地调整猜测谱，使价值函数J最小化，来反演获得最优的海浪谱。价值函数J的定义如下：

式中，P(k)表示SAR 图像谱，(k)表示根据非线性关系由猜测谱正演得到的模拟SAR 图像谱，(k)表示第一猜测谱，F(k)表示反演的最优谱，μ为权重系数，B为防止分母为0时设置的小正数。在价值函数J的表达式中，第一项表示观测的和模拟的SAR 图像谱的差，第二项表示第一猜测谱与反演谱的偏差。当价值函数最小时，反演谱对应的模拟SAR 图像谱最接近真实的SAR 图像谱，同时，反演获得的海浪方向谱也最接近第一猜测谱。

MPI 算法最早应用于欧空局ERS 卫星波模式数据，为ERS 卫星波模式UWA（SAR Wave Fast Delivery Product. Wave Spectra）谱产品设计了程序接口。因此，本文参照了UWA 产品手册来计算S1 SAR 图像谱并进行编码处理（Brooker，1995）。本文采用1024 像素×1024 像素的窗口（约10 km×10 km）对S1的SAR图像进行分割，将得到的每一个子图像作为反演的一个单元。为减少图像谱的噪声，本文又将子图像按512 像素×512 像素窗口分为4个部分，分别计算图像谱并通过平均得到一个较平滑的子图像谱。为避免SAR 子图像中存在岛屿、油膜、海冰等现象或特征而导致海浪反演误差大甚至错误，需要在进行图像谱计算前对子图像进行均质性检测。采用均质性参数ξH，即图像功率谱的方差和均值的比值：

定量描述该子图像是否为均匀一致的。式（4）中，φk表示分割后的子图像的功率谱密度，和分别表示功率谱密度的均值和方差。对于均匀SAR 海表图像，其均质性参数ξH接近于1，而对于不均匀的SAR 图像，ξH往往大于1。本文中采用1.05 作为阈值，当均质性参数小于1.05 时，方进行图像谱计算（Schulz-Stellenfleth和Lehner，2004；Li和Huang，2020；Wu等，2021）。

2.3 数据时空匹配

在MPI 反演过程中，本文将根据待反演的SAR 子图像中心经纬度匹配空间距离最近的WW3模式网格点，再提取该网格点上与SAR 过境时间最接近时刻模式数据作为反演所需的第一猜测谱。参考MPI 算法应用于ERS 波模式SAR 数据反演时使用的窗口尺寸，本研究中采用3 h 和3°作为SAR子图像与模式数据匹配的最大距离。需要指出的是该距离仅为进行反演的最宽松时空匹配条件，在实际匹配过程中，匹配到的数据时间差未超过0.5 h，91%的数据空间距离未超过0.5°。

本文分别采用了SWIM 10°入射角下的谱数据以及其星下点的有效波高数据对SAR 反演的海浪方向谱和有效波高等参数进行对比验证。由于10°入射角下谱产品覆盖范围、SWIM 星下点的足印面积以及SAR 子图像的尺寸存在较明显差异，因此本文在SAR数据与SWIM数据的时空匹配中采用了不同空间匹配原则（详述如下），但时间匹配窗口均≤1.5 h。

在SWIM 谱数据与SAR 反演谱数据的匹配中，本文直接通过平均SWIM 谱产品覆盖区域内的全部SAR 子图像谱来计算新的图像谱，并根据SWIM 谱的中心经纬度以及SAR 数据的过境时间来匹配最接近的WW3 模式谱数据，进而反演得到与SWIM谱时空匹配的SAR 海浪方向谱，匹配示意图如图2所示。图2 中蓝色方块表示SWIM 谱的中心经纬度，黑框表示SWIM 波谱仪10°入射角下谱的大致覆盖范围。由于IW 数据幅宽较宽、分辨率较高，对全部SAR 数据进行图像分割及反演需要较长时间，并占据较多计算资源，因此在本研究中只选取了25景SAR数据开展海浪谱的反演及对比验证，包含15景VV极化数据和10景HH极化数据，每景数据均能匹配到3 个以上SWIM 谱数据。排除部分反演失败和无效的SWIM 谱数据，最终匹配到的有效谱数据对为54对。

图2 SWIM谱数据与SAR数据的匹配示意图（蓝色方框表示SWIM谱的中心经纬度，黑色方框表示其中一个SWIM谱的大致覆盖范围）Fig. 2 Illustration of collocation between a SWIM spectrum（The blue squares denote the center locations of SWIM spectra and the black box represents the coverage of a SWIM spectrum）and a S1 SAR image

在SWIM 星下点有效波高的空间匹配中，本文使用了114景S1 SAR数据，直接以SWIM星下点经纬度为中心，提取1024 像素×1024 像素大小的子图像进行海浪方向谱的反演，并积分计算得到海浪的有效波高和平均波周期参数。最终成功匹配有效波高数据对共5075对。

3 反演结果及分析

3.1 海浪方向谱的反演及对比验证

本文首先展示一个SAR 海浪方向谱反演个例。以2020 年9 月29 日16：24：54 UTC 时间过境的S1 SAR 数据为例。图 3 给出中心经纬度为71.88°N，14.73°E处的海浪方向谱反演及其对比结果。

图3（a）和（b）分别为SAR 子图像谱以及WW3 模式谱数据（模式数据时间为2020 年12 月29日16：00 UTC，模式网格点经纬度为72°N/14.5°E）。图中用同心圆圈对波长进行标注，从外至内依次为50、100、200、500 和800 m。SAR 图像谱和模式谱数据展示了一组向东北方向传播的海浪，SAR图像谱数据计算得到海浪传播方向为北偏东41°，主峰波长约为224 m；模式谱提供的数据表明海浪的传播方向为北偏东60°，主峰波长为196 m。图3（c）和（d）分别为SAR 反演的海浪方向谱数据和10°入射角下获取的SWIM 谱数据。根据反演的海浪方向谱结果显示，海浪的传播方向为北偏东49°，主峰波长为215 m，较模式数据更接近SAR 图像谱参数。对比SWIM 谱可以发现，SWIM谱中也揭示了一组向东北方向传播的海浪，其波长在200 m 左右。此外，在SWIM 谱的低频区域（波长约400 m 以上）也有较高的谱能量分布，该信号产生的可能原因是SWIM 斜率谱在向波高谱转换的过程中，谱值除以分母k2后导致低频部分残留的噪声被放大。通常，该噪声信号在一维谱中更为显著，表现为低频区域中出现较为显著的谱峰，称为寄生谱峰（Hauser 等，2021）。在对反演的海浪方向谱与SWIM 谱的对比个例研究中发现，SAR 反演的海浪方向谱在谱形结构、能量分布等方面与SWIM谱数据都具有良好的一致性。

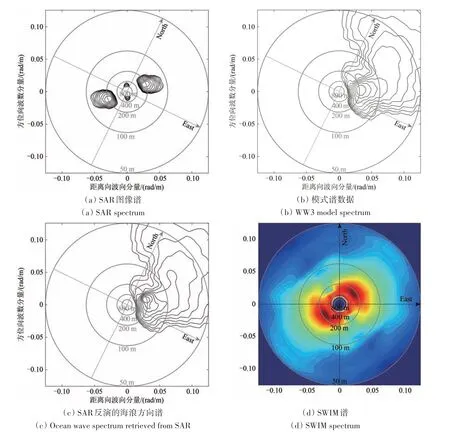
图3 海浪方向谱反演结果与SWIM谱的对比Fig. 3 Comparison between the SAR retrieved ocean wave spectrum and the SWIM spectrum

SWIM 波谱仪在10°入射角下除了提供斜率谱数据以外，还提供了谱的有效波高等积分参数。为定量的验证SAR 海浪谱反演结果的准确性，本文采用以下公式对SAR 反演的海浪方向谱进行积分，计算得到海浪的有效波高Hs、平均波周期等参数Tm02。

式中，f和θ分别表示谱的频率和方向，mn表示谱的n阶矩。

由于SWIM 的谱产品中并未直接给出平均波周期参数，本文参考海浪谱平均波数的计算公式（式（8））以及深水频散关系式（9），计算得到SWIM 谱的平均波周期参数。同时，本文也对SWIM 测量的谱以及SAR 反演的波高谱进行了平滑，并提取了谱峰的传播方向及波长。谱参数对比结果如图4所示。

为定量说明反演结果的精度，本文采用了偏差（Bias）、均方根误差（RMSE）、散度指数SI（Scatter Index）和相关系数（Correlation）等4种统计参数对反演结果精度进行定量描述。其中，散度指数计算公式如下式（10）。

式中，X和Y分别表示SWIM 波谱仪的测量结果以及SAR的反演结果，N表示数据集的数量。

图4（a）和（b）分别展示了SAR 海浪方向谱积分的有效波高和平均波周期参数与SWIM 谱积分参数的对比。从对比结果可以看到，两个数据集具有较好的一致性。有效波高比较得到的偏差和均方根误差分别为0.11 m 和0.71 m，相关系数为0.90，散度指数为21.12%；平均波周期比较得到的偏差及均方根误差分别为-0.52 s 和0.62 s，相关系数和散度指数分别为0.93和4.32%。

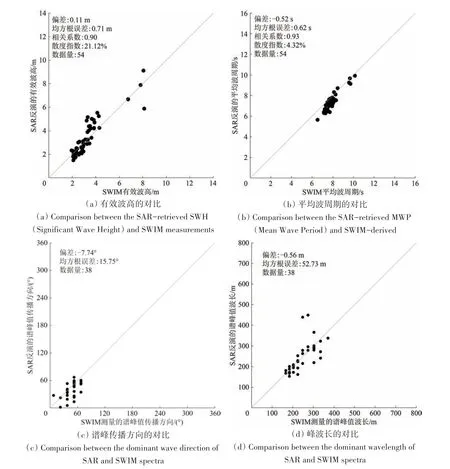
图4 SAR海浪方向谱参数与SWIM谱数据积分参数的对比Fig. 4 Comparisons of the ocean wave integral parameters by SAR-retrieved ocean wave spectra and SWIM slope spectra

在谱峰波长和传播方向等参数对比分析过程中，考虑到SWIM 波高谱低频区域的噪声可能会对谱峰位置判断产生影响，本文对比分析了SWIM 谱和WW3 模式谱的一维谱来判断SWIM 谱中是否存在显著的寄生峰，并对谱峰波长与寄生峰波长接近的数据进行了去除，最终匹配得到谱峰参数对38 对。谱峰传播方向和谱峰波长的对比结果分别如图4（c）和（d）所示。S1 SAR反演的谱峰的传播方向与谱峰波长均与SWIM 测量结果较为接近，谱峰传播方向的偏差和均方根误差分别为-7.74°和15.75°，谱峰波长的偏差和均方根误差分别为-0.56 m和52.73 m。

3.2 有效波高反演结果及对比验证

为进一步验证S1 SAR 海浪参数反演结果准确性，本文开展了SWIM星下点处S1 SAR海浪谱积分的有效波高结果与SWIM 测量结果的交叉验证，结果如图5 所示。由于SWIM 星下点有效波高数据产品采样更为密集，采样间隔约为1.5 km，而SWIM的10°入射角下获取的谱数据是由70 km×90 km 范围内所有独立测量结果合成的，因此，SWIM 星下点匹配的数据量远超谱数据匹配的数据量。从图5中可以看到S1 SAR 反演的有效波高结果与SWIM星下点的测量结果有着更好的一致性。二者的偏差和均方根误差为0.03 m 和0.48 m，相关系数为0.95，散度指数为15.88%。

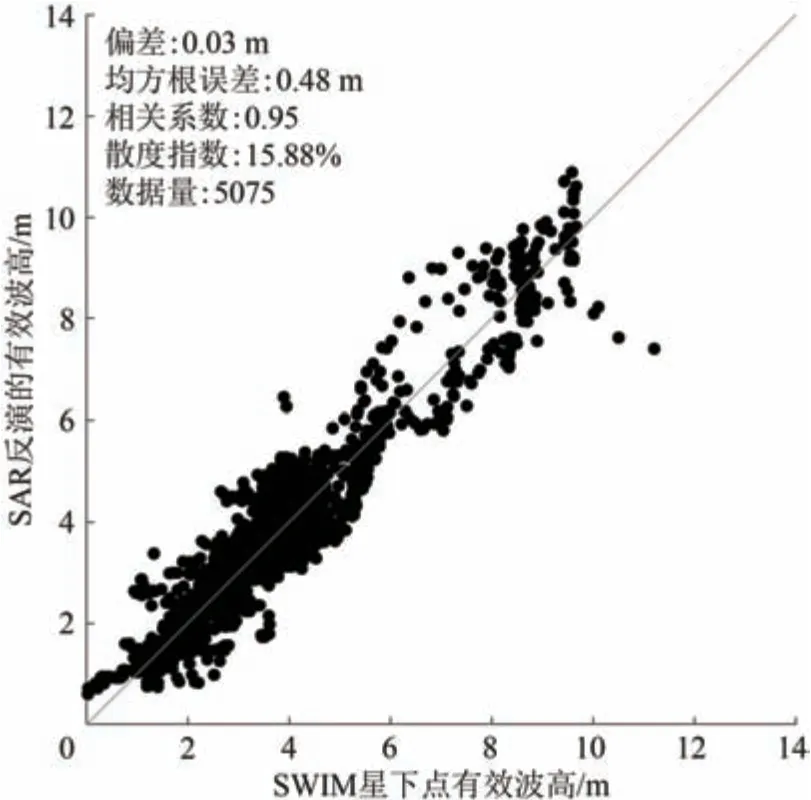
图5 SAR反演的有效波高结果与SWIM波谱仪星下点的测量结果的对比Fig. 5 Comparison of the SAR-retrieved SWH with the SWIM nadir measurements

4 结 论

本文基于MPI 海浪方向谱反演方法，利用了哨兵1 号的高分辨率IW 数据在格陵兰海和挪威海海域开展了海浪方向谱的反演研究。同时，利用了SWIM 波谱仪提供的海浪谱及海浪有效波高等数据，对S1 SAR 反演结果进行了验证。一方面，本研究为北极海冰—海浪的相互作用研究提供方法和数据基础。另一方面，本研究展示了S1 SAR 数据和SWIM 波谱仪数据可互为验证数据集，二者互补，有望能够提高北极海浪方向谱数据的时空覆盖率，为全面刻画北极海浪信息提供重要数据集。

研究选取了2020年9月的25景IW 数据，进行了SAR海浪方向谱反演以及反演结果与SWIM谱数据的验证。对比结果表明SAR 反演的海浪方向谱从谱型结构、能量分布、传播方向、积分参数等方面与SWIM 测量的斜率谱都具有较好的一致性。SAR 反演的有效波高的偏差和均方根误差分别为0.11 m 和0.71 m，相关系数和散度指数分别为0.90和21.12%；平均波周期的偏差和均方根误差分别为-0.52 s 和0.62 s，相关系数和散度指数为0.93 和4.32%；谱峰传播方向偏差和均方根误差为-7.74°和15.75°，谱峰波长的偏差和均方根误差分别为-0.56 m和52.73 m。

本文选取了114 景SAR 数据进行了SWIM 星下点处有效波高的反演及对比，反演并匹配到数据对5075 对。对比结果显示，相较于SWIM 10°入射角下海浪谱积分得到的有效波高，SAR 反演的有效波高与SWIM 星下点测量结果具有更好一致性，偏差和均方根误差分别为0.03 m和0.48 m，相关系数和散度指数分别为0.95 和15.88%。产生上述结果的原因可能有两方面，一方面，SWIM 10°入射角条件下获取的海浪谱代表了70 km×90 km 大范围的测量结果，即便把该区域内所有SAR 子图像谱平均作为MPI 算法输入，两者仍然可能存在较大差异。另一方面，由于SWIM 谱数据的噪声去除算法和调制传输方程都还有待提升，SWIM 10°入射角条件下获取的海浪谱反演精度也待进一步提高（Hauser等，2021）。

本研究验证了利用MPI反演方法以及哨兵1号IW 数据在北极海域进行海浪方向谱及参数反演的可行性。尽管MPI 方法在应用方面依然存在一些限制，最突出的就是依赖于先验信息，但是该方法仍然是目前可以得到高分辨率海浪方向特征参数的有效方法。基于该方法反演获得的海浪方向谱数据是研究海浪向冰传播过程海浪各频率、各方向上的能量衰减过程及波向变化的关键数据。

志 谢本文中使用的哨兵1 号SAR 数据及SWIM波谱仪数据分别由欧洲航天局和法国国家空间局卫星海洋学存档数据中心AVISO+提供。同时感谢国家海洋环境预报中心为本研究提供了大量的WW3模式数据。在此表示衷心的感谢！