HY-2卫星微波散射计海面风场地球物理模式函数研究

王志雄， 邹巨洪， 林明森， 林文明， 张有广，李秀仲， 冯倩， 何宜军

1. 南京信息工程大学 海洋科学学院, 南京 210044;2. 南方海洋科学与工程广东省实验室(广州), 广州 511458;3. 自然资源部空间海洋遥感与应用重点实验室, 北京 100081;4. 国家卫星海洋应用中心, 北京 100081

1 引 言

当前，中国海洋卫星系列实现了组网业务化运行，其中海洋二号（HY-2）系列卫星搭载主动和被动微波遥感器，主要实现对全球海洋动力环境要素的卫星组网观测（蒋兴伟 等，2016，2019）。微波散射计是HY-2系列卫星的主要载荷之一，通过测量海洋表面的雷达后向散射系数实现对全球海面风场（风速和风向）和极地海冰（海冰范围和类型等）的遥感观测（Liu，2002；刘建强 等，2021；赵朝方 等，2019）。

海洋表面的雷达后向散射系数不仅与微波散射计的雷达系统有关（主要是波段、极化方式、入射角、方位角），也由海面状态决定（主要是厘米尺度的波浪、海表温度和海流）；而海面风场是海面波浪形成的主要驱动力。基于此，把定量表达海面雷达后向散射系数、海面风速风向等主要地球物理参数和雷达观测方式之间关系的函数称为地球物理模式函数GMF （Geophysical Model Function）。可见，GMF 是影响星载微波散射计海面风场反演精度的关键因素之一。GMF 的构建主要采用半经验方法；通常以数值天气预报模式预报风场或海面风场遥感数据作为参考海面风场，基于海面后向散射系数观测数据对GMF 模型参数进行分析拟合的方式构建。因此GMF 的准确性在一定程度上受到卫星数据和参考风场数据的制约。以Wentz和Smith（1999）基于Ku波段NSCAT散射计数据构建的NSCAT-2 GMF为例，由于NSCAT散射计采用固定天线扇形波束体制，观测入射角范围较大（16°—66°），使得NSCAT-2 GMF具有较好的普适性，涵盖了迄今所有Ku 波段卫星散射计的观测入射角和极化方式（水平和垂直极化）。然而受NSCAT 观测数据量少（仅有9 个月），以及当时ECMWF 和SSMIS 辅助数据质量等因素的影响，NSCAT-2 GMF 的准确性不够高。研究表明基于NSCAT-2 GMF 处理QuikSCAT/SeaWinds、OceanSat-2/SCAT 和HY-2A/SCAT 等卫星散射计数据得到的反演风速存在显著误差（Wang 等，2019；Zhao等，2021）。这种情况下，美国针对QuikSCAT 散射计开发了Ku-2011 GMF（Ricciardulli 和Wentz，2015），印度针对OceanSat-2/SCAT 散射计开发了OSCAT-specific GMF （Gohil 等，2013），而欧洲荷兰皇家气象研究所（KNMI） 则是通过校正NSCAT-2 GMF 的风速依赖关系得到了NSCAT-4 GMF（https://scatterometer.knmi.nl/nscat4_gmf/［2022-05-23］）。

近年来，ISS/RapidScat 和HY-2C 等微波散射计搭载在非太阳同步轨道卫星上运行，使得同期在轨运行的Ku 和C 波段卫星散射计产生大量全球分布的匹配数据。这为研究海面风场遥感产品的一致性、海面风场GMF 研究等提供了契机。Wang等（2017a）研究表明，Ku波段海面后向散射系数受到海表温度（SST）的影响十分显著。若Ku 波段GMF 中没有SST 因子项（如NSCAT-4 和Ku-2011 GMF），则反演风速的误差将呈现显著依赖于SST 的特征。因此有必要在Ku 波段GMF 函数中加入SST 因子；相对而言，SST 对C 波段海面后向散射系数的影响可以忽略不计。Wang等（2017b）基于NSCAT-4 GMF 构建了用于Ku 波段RapidScat 卫星散射计且包含SST 因子的GMF，该研究提出了SST 因子项系数的拟合方法，并且验证了GMF 中引入SST因子项可以进一步提高风场反演精度。

基于上述研究，国际上最新发布的Ku 波段卫星散射计海面风场产品的反演算法中均使用了包含SST 因子的GMF。例如，美国JPL 于2018 年发布了重新处理的QuikSCAT/SeaWinds（版本V4 和V4.1）和ISS/RapidScat（版本V2）散射计海面风场产品（https://podaac.jpl.nasa.gov/［2022-05-23］）；欧洲KNMI 在Ku 波段卫星散射计数据处理的业务算法中使用了NSCAT-4DS+SST 校正项的GMF（参见KNMI 官网https://scatterometer.knmi.nl/nscat_gmf/［2022-05-23］）。

2021 年5 月25 日，中国海洋二号D 卫星成功发射，标志着中国海洋动力卫星三星组网观测星座正式形成。HY-2B/C/D 卫星采用一颗太阳同步轨道、两颗倾斜轨道的独特组网方式。这为HY-2B/C/D 卫星之间，以及HY-2 卫星与欧洲C 波段散射计在全球范围内获取交叉匹配数据，进而构建适用于HY-2系列卫星微波散射计的新型地球物理模式函数的研究提供了契机。本文旨在构建一种适用于HY-2 系列卫星微波散射计且含SST 因子项的新型地球物理模式函数（命名为NSCAT-5.HY-2 GMF），并对其应用效果进行分析。

2 研究数据

2.1 HY-2系列卫星微波散射计数据

当前在轨运行的HY-2 系列卫星包括HY-2B、HY-2C和HY-2D卫星；其中HY-2B星为太阳同步轨道且升交点地方时约为18：00 UTC；HY-2C 和D星均为顺行倾斜轨道（倾角约为66°），卫星经过某地的当地时间在0：00 至24：00 漂移；三星组网的卫星轨道设计极大提高了卫星数据对全球海洋的时空覆盖能力，其微波散射计累计12 h 可以覆盖全球＞96%的海洋。

HY-2 系列卫星微波散射计（HSCAT）采用Ku 波段旋转扫描体制，通过内外两个固定入射角的笔形波束测量地球表面的归一化雷达后向散射截面（也称为后向散射系数，常用符号σ0表示）；内波束采用水平（HH）极化方式，而外波束为垂直（VV）极化。HSCAT 散射计每个波束发射的脉冲信号在地面的足印大小约为25 km×32 km（方位向×距离向），回波信号经过内定标计算得到该地面单元的后向散射系数（Zhang 等，2021）。Wang等（2021）通过3种定标方法验证了HY-2系列B、C 和D 星3 个平台的微波散射计σ0数据具有很好的一致性，总体相对定标偏差小于0.1 dB。HSCAT-B、HSCAT-C 和HSCAT-D 散射计σ0数据之间的高度一致性为GMF 研究，以及反演具有高度一致性的海面风场提供了条件。HSCAT 散射计σ0数据通过面元匹配重采样到分辨率为25 km 的沿着顺轨和交轨方向划分的地面网格单元（风矢量单元），并用对每个风矢量单元进行风矢量反演，得到空间分辨率为25 km的海面风场数据（邹巨洪 等，2017）。本研究使用HSCAT散射计25 km分辨率的数据。

下文研究中，HSCAT-B 和C 散射计数据的时间范围为2020 年10 月至2021 年11 月，HSCAT-D数据的时间范围为2021年6月至2021年11月。

2.2 HSCAT与ASCAT微波散射计配对数据

欧洲MetOp 系列A、B 和C 卫星都搭载了微波散 射 计ASCAT，由 于MetOp-A 于2021 年11 月15 日结束了为期15 年的业务运行，目前仅MetOp系列B 和C 卫星提供业务化遥感数据产品。MetOp系列卫星运行在相同的太阳同步轨道面，升交点地方时约为21：30 UTC。ASCAT 散射计采用C 波段VV极化的观测方式，目前主要提供分辨率为25 km、12.5 km 和5.6 km 的 海 面 风 场 产 品（Verhoef 等，2012；Vogelzang 和Stoffelen，2017）。本研究选用ASCAT-B 和ASCAT-C 散射计25 km 分辨率的海面风场产品，ASCAT 数据的时间范围与HSCAT 数据对应。

研究表明，不同于Ku 波段散射计，C 波段散射计测量海面后向散射系数和遥感风场产品不受到海表温度变化的影响。基于此，本文研究将以ASCAT 海面风场数据为参考，研究用于HSCAT 散射计海面风场反演的GMF。在匹配ASCAT 与HSCAT数据过程中，限制空间距离小于观测时间差小于45 min。此外，根据ASCAT 和HSCAT 数据产品中的质量标识等信息，进一步根据数据产品中质量控制标识筛除受降雨影响等质量较差的数据。

海表温度数据采用ECMWF ERA5模式在06：00和18：00 UTC 时刻的再分析数据。在对每个ASCAT 或HSCAT 数据匹配SST 的过程中，采用空间二维线性插值，但在时间上则选取最近时间点的SST数据（匹配时间差最大为12 h）。

3 NSCAT-5.HY-2 GMF构建

本研究旨在构建适用于中国HY-2卫星微波散射计海面风场反演的GMF；该工作将基于现有NSCAT-4 GMF，分别改进海面后向散射系数随风速和风向的变化关系，并且增加SST因子项，将改进后的GMF 称为NSCAT-5.HY-2 GMF。需要注意的是，尽管SST 对海面σ0的影响与观测入射角有关，但由于HY-2 卫星微波散射计采用固定入射角，因此本研究不考虑观测入射角的变化。

在不考虑入射角变化的前提下，Wang 等（2017b）在前人研究基础上提出了包含SST因子项的Ku波段GMF 的数学模型。参考该研究提出的数学模式，本研究中NSCAT-5.HY-2 GMF 的数学模型采用如下形式：

式中，p表示极化方式（VV 或HH）；V表示海面10 m高处的风速；φ表示雷达观测方向与海面风向的夹角；T表示海表温度；T0表示参考温度，与风速V有关；N取值为4，即风向调制采用5 项傅里叶级数表达；表示简谐项系数；表示多项式系数。由式（2）可知，在给定极化方式和风速的条件下SST 对Ku 波段σ0影响的大小可以表示为SST相对值（相对于参考温度T0）的二次多项式。

由式（1）可知：（1）在地球物理模式函数中增加SST影响是通过增加海表温度因子项yp得以实现。在给定入射角和风速条件下，σ0随海表温度变化的关系采用二次多项式（式（2））表达；（2）海表温度影响在各个风向φ上各向同性；（3）系数A0p(V，T0)主要表示σ0对入射角和风速的依赖关系，其中风速影响占主导地位；（4） 风速因子项（A0p(V，T0)）、风向调制项（傅里叶级数）和海表温度因子项yp之间具有相对独立性。

本研究中GMF 的构建将基于ASCAT-B 与HSCAT-C 配对数据集，数据时间范围为2020 年10 月至2021 年9 月。下面将基于NSCAT-4 GMF 反演HSCAT散射计获得的海面风场表示为HSCAT/N4。

本研究NSCAT-5.HY-2 GMF 的构建主要包括3个部分。基于现有NSCAT-4 GMF在HY-2散射计观测入射角处：（1）改进σ0随风速变化的关系，结果是校正了式（1）中的表达风速依赖关系的系数；（2）改进不同风速条件下σ0随风向变化的关系，即重新拟合式（1）中的谐波项系数；（3）定量计算不同风速条件下σ0随海表温度变化的关系，即拟合式（2）中的多项式系数。下文依次介绍。

3.1 海面后向散射系数随海面风速变化的关系

风速是影响海面雷达后向散射系数大小的主要因素，在GMF 中风速因子项（系数A0p）占主导地位。GMF 中A0p项对散射计反演风场的风速概率密度函数（PDF）分布具有决定性作用。Stoffelen等（2017）在研究C 波段CMOD7 GMF 过程中验证了采用累积分布函数（CDF）配准方法可以校正风速误差。本研究基于ASCAT-B 与HSCAT-C/N4 数据的配对数据集开展，选取ASCAT-B 海面风速CDF 为参考CDF（记作Cref），通过将HSCAT-C/N4风速CDF （记作CN4） 配准到Cref的过程得到HSCAT-C/N4 在不同风速条件下的风速校正量（ΔV）。具体而言，对于HSCAT-C/N4的反演风速x，可以找到风速使得CN4(x)=Cref()。则在风速x处的风速校正量为ΔV(x)=-x。认为HSCAT-C/N4的风速偏差ΔV主要是由于NSCAT-4 GMF误差造成的，只要将NSCAT-4 GMF偏移ΔV即可消除该偏差。

采用CDF 配准方法计算HSCAT-C/N4 反演风速的校正量，结果如图1 所示。图1 中蓝色粗实线表示校正量计算结果，红色细实线表示实际应用的校正量（即对NSCAT-4 GMF 的风速校正量）。需要注意的是，在低风速（小于2 m/s）和高风速（大于20 m/s）条件下对GMF 的实际风速校正量进行了约束处理，这主要是因为：一方面，该风速区间的数据量较少；另一方面，该风速条件下配对数据的客观一致性较差；ASCAT 风速不能很好地代表HSCAT 数据对应的“真实”风速（若风速为2（20） m/s，则45 min 对应的空间范围约为5.4 （54） km）。

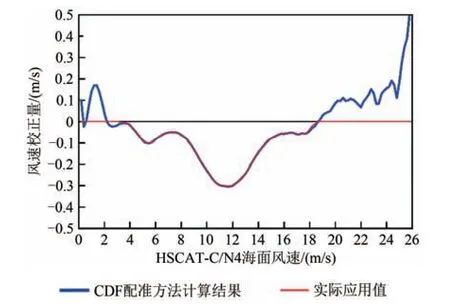
图1 使用CDF配准方法得到的HSCAT-C/N4风速校正量Fig. 1 Wind speed corrections as a function of wind speed using CDF matching technique

3.2 海面后向散射系数随海面风向变化的关系

以ASCAT-B 风向为参考风向，改进NSCAT-4 GMF 在HSCAT 入射角处的风向依赖关系。该研究中特别需要去除非风向调制误差（如风速）导致的风速偏差对研究结果的影响，即只关注式（1）中的风向调制项。为此，定义如下表达式：

式中，Jp(V，φ)表示极化p、风速V和风向φ对应的NSCAT-4 GMF 的校正量；表示HSCAT 测量表示基于NSCAT-4 GMF且以ASCAT 风速和风向、HSCAT观测几何为输入得到的仿真σ0；和分别表示在风速V条件下所有测量及对应仿真σ0数据的平均值。

式中，表示NSCAT-4 GMF 在HSCAT 入射角条件下给出的σ0。

将ASCAT-B 与HSCAT-C 配对数据按风速1.0 m/s和风向2.5°为间隔进行分组，计算每个风速区间校正后的风向调制Dp(V，φ)，进而采用5项傅里叶级数进行拟合并得到拟合系数4］），结果如图2 所示。在此基础上，采用三次样条插值法对各风速区间的谐波项系数进行后处理并获得随风速连续变化的系数（图2 中实线）。在该拟合过程中对低风速（小于2 m/s）和高风速对应的谐波项系数进行了约束。对于平静海面（风速很低），在海面观测单元（25 km×25 km）内风速和风向的空间变率相对较大，这模糊了散射计测量σ0对风向变化的敏感性。

由图2可见，尽管在风向调制中三次和四次谐波项（即和）的对风向调制幅度的贡献较小，但系数随风速变化十分显著，并且HH 和VV 极化σ0随风向变化的关系显著不同。

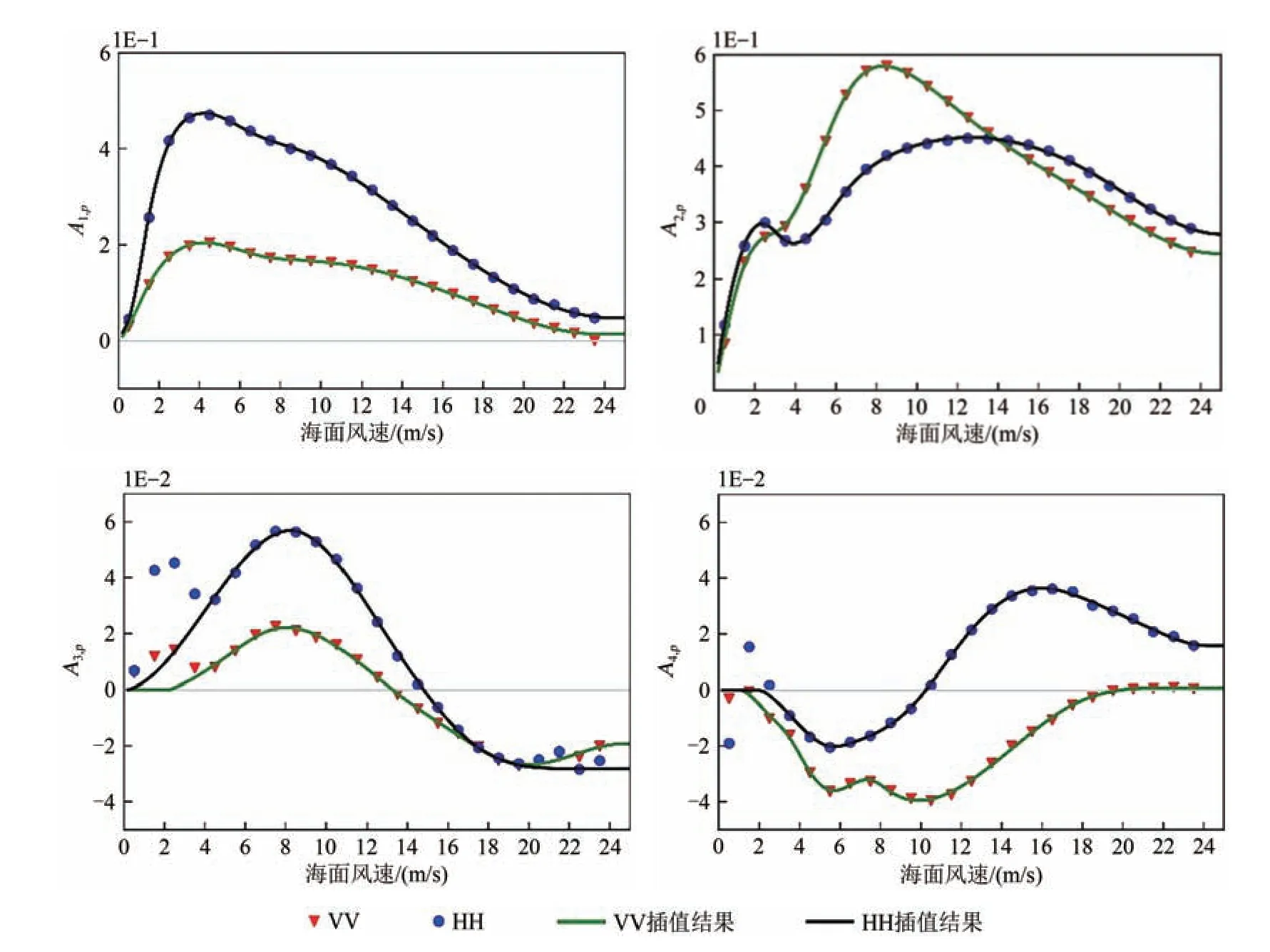
图2 风向调制的谐波项系数（散点数据为基于分组数据得到的每个风速区间的谐波项系数；实线为基于散点数据插值平滑后的谐波项系数）Fig. 2 Harmonic coefficients for wind direction modulation （points correspond to harmonic coefficients based on collocated scatterometer data； solid lines correspond to smoothed harmonic coefficients as a function of wind speed）

3.3 海面后向散射系数随海表温度变化的关系

Wang 等（2019）提出了推算和拟合SST 因子项（即式（2））各系数的方法，并且通过Ku 波段ISS/RapidScat 散射计数据验证了该方法的有效性。本文采用同样的方法得到系数，简要介绍如下。自定义函数fp和gp：

式中，T表示海表温度（℃）；T0为自由设定的参考温度，本研究中令T0(V) ≡12.5 ℃；需要注意的是，假设了海表温度影响在各个风向φ上各向同性；因此在上式中省略了风向符号。

结合式（1）和（2）可知，函数gp剥离了风速和风向对σ0值的贡献，只关注给定风速条件下海面σ0相对值（T相对于T0）随SST 变化的关系。换言之，函数gp给出了SST变化量（ΔT=T-T0）对应的σ0变化量。将ASCAT-B 与HSCAT-C 数据按照风速1 m/s 和海表温度1 ℃的间隔进行分组，再对每个风速和SST 数据组内观测和仿真σ0数据分别求均值得到和进而计算每个风速区间的函数gp。再没有噪声影响的情况下，函数gp等同于式（1）定义的SST 因子项yp。但实际研究数据存在多种误差（如HSCAT观测误差，ASCAT 数据误差，选取参考温度T0带来的误差）干扰。为减小误差影响，采用式（8）进行数据拟合。

若在理想情况下，式中a= 1；通过引入参数a能够改善对曲线的拟合效果，参数拟合的结果如图3所示。图中VV和HH极化分别用红色和蓝色表示，散点为各风速区间的参数拟合结果，实线为采用三次样条插值方法对拟合参数后处理得到的系数或。与前文相同，在低风速和高风速情况下研究数据的噪声相对较大，在得到系数或随风速变化关系的过程中，剔除了部分数据点并增加了约束条件。

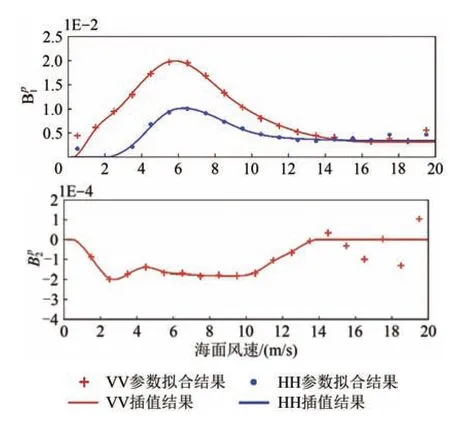
图3 SST因子项的系数Fig. 3 Coefficients of SST dependence

由图3 可见，VV 极化σ0随SST 变化的关系主要为1 次项的贡献（近似线性关系），而二次项的贡献非常小。本文同样采用了2 次多项式拟合了HH 极化数据，但分析发现二次项系数随风速变化的关系不规律。由于HH 极化2 次项的贡献较小，使得噪声影响相对较大，从而导致过度拟合；基于此，认为采用线性关系（摒弃2次项）拟合结果可以更准确地表达HH极化σ0随SST变化的关系。

现有NSCAT-4 GMF 的建立使用了全球样本数据，所提供的可以理解为相同(V，φ，θ，p)条件下海面σ0数据的平均值。在这个GMF 构建过程中虽然没有考虑每个σ0受到SST的影响，但其结果是平均了所有σ0受到SST 的影响。由此可知，与海面某SST 值对应的σ0相等，我们把该SST 值表示为TN4。进一步分析认为，TN4随风速变化显著，而相对风向变化的关系不显著（忽略不计）。本研究用ASCAT-B 和HSCAT-C配对数据的每个风速区间内所有数据对应SST的均值作为TN4。一方面，本文3.1节中基于同样的数据集获得了GMF 中风速的依赖关系；另一方面，ASCAT-B 与HSCAT-C 配对数据的地理分布广泛且具有较好的代表性。

综上可知，以TN4作为式（1）和（2）中的参考温度T0，则对NSCAT-4 GMF（HSCAT 散射计入射角） 而言SST 影响下后向散射系数的校正量为

基于式（2）和式（9）以及系数或，分别计算VV 和HH 极化在给定风速和SST 条件下的海面后向散射系数的校正量，结果如图4 所示。图4 中颜色表示相同风速条件下某SST 值对应σ0与参考温度TN4（黑色虚线）对应σ0的相对值。

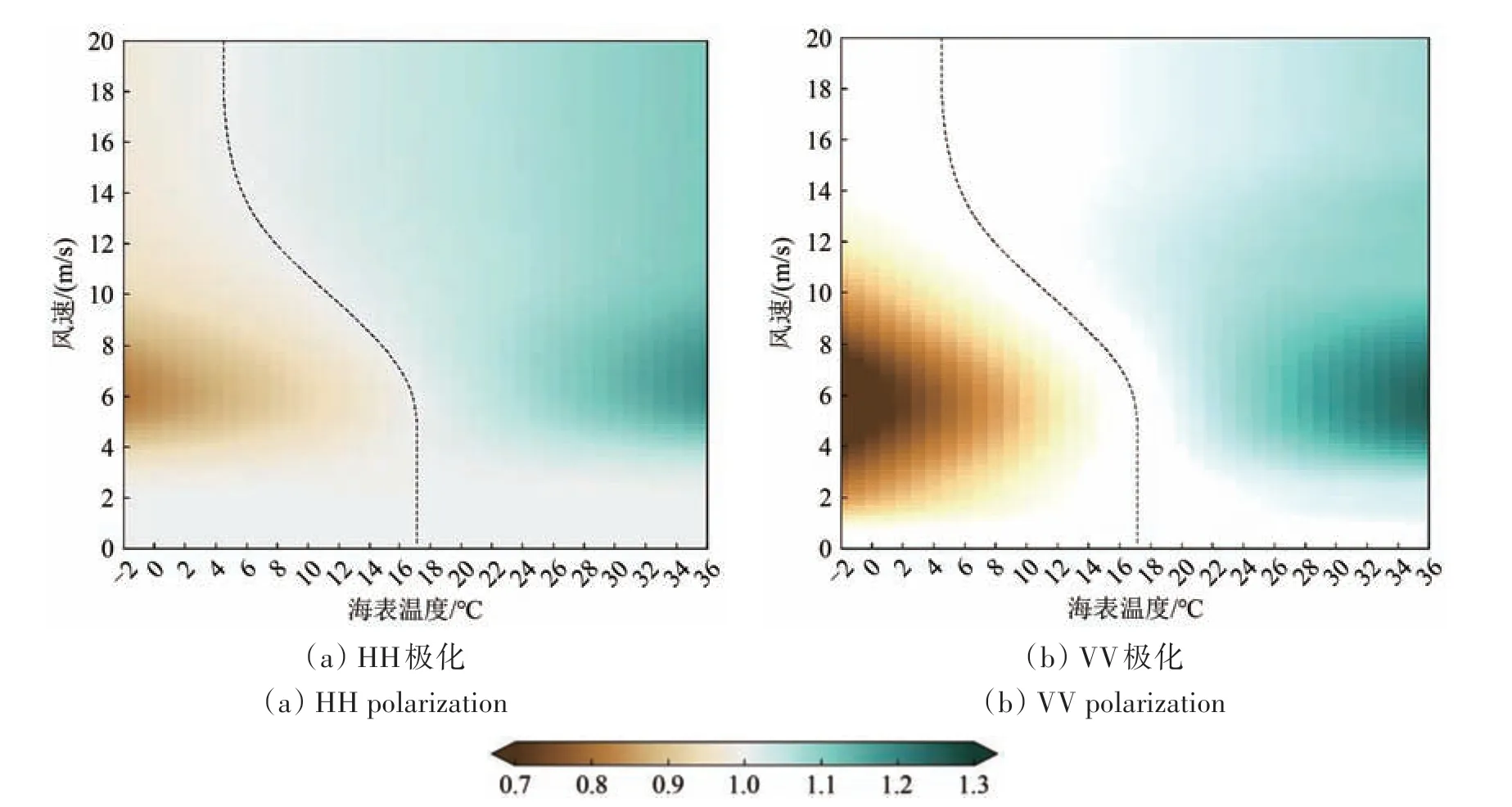
图4 SST影响下后向散射系数的校正量（图中颜色表示后向散射系数的相对值，黑色虚线表示TN4(V)）Fig. 4 Backscatter corrections for SST effects （Color represents the relative values of backscater coeffieients，black dasked line stands for TN4(V)）

3.4 小结与结论

本研究以式（1）和（2）作为NSCAT-5.HY-2 GMF 的数学模型，其中风速、风向和SST 依赖关系具有相对独立性。基于ASCAT-B和HSCAT-C/N4配对数据，通过3 个研究过程分别得到了σ0对风速、风向和SST的依赖关系。

（1）以ASCAT-B 风速为参考风速，采用CDF配准方法得到了HSCAT-C 反演风速的校正量ΔV(V)；该校正量主要是由NSCAT-4 GMF 中风速依赖关系的误差造成的。将NSCAT-4 GMF 偏移ΔV即可修正。

（2）以ASCAT-B 风速和风向为参考数据，计算给定风速V条件下每个风向的校正量Jp(V，φ)，进而得到给定风速V所对应的风向调制Dp(V，φ)；采用5 项傅里叶级数进行拟合Dp得到谐波项系数

（3）以ASCAT-B 风速为参考风速，计算给定风速V条件下海面σ0相对值（T相对于T0≡12.5℃）随SST变化的关系，即gp(V，T)；通过拟合gp得到SST 因子项系数和；进一步，结合NSCAT-4 GMF 固有TN4(V)计算得到各风速和SST 条件下的σ0校正量

4 NSCAT-5.HY-2 GMF 在HY-2 系列卫星微波散射计海面风场反演中的应用效果

采用NSCAT-4.HY-2 GMF 反演HY-2B、C 和D 散射计数据，把得到的海面风场记作HSCAT-B/N5、HSCAT-C/N5和HSCAT-D/N5。研究数据的时间范围如2.1节所述。

4.1 HSCAT风速偏差随风速变化的关系

本研究中以ASCAT-B 散射计海面风场作为了参考风场，该过程也实现了HSCAT 与ASCAT 散射计海面风场的交叉校正。图5 给出了HSCAT-D 与ASCAT-C 风速对比结果，包括偏差和方差（SD）随二者平均风速变化的关系。风速在25 m/s 以内，HSCAT-D/N5与ASCAT-C风速偏差不再显著依赖于风速变化，各风速区间的风速偏差均小于0.1 m/s。

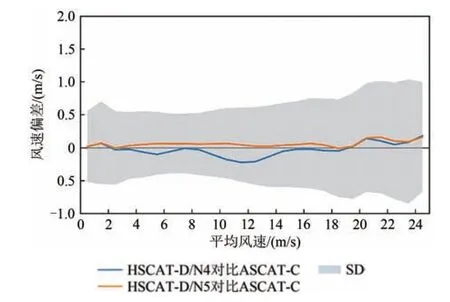
图5 HSCAT-D与ASCAT-C风速偏差随两者平均风速变化的关系Fig. 5 Wind speed biases between HSCAT-D and ASCAT-C as a function of wind speed

4.2 HSCAT风速偏差随SST变化的关系

海表温度影响主要导致依赖于SST变化的风速偏差。图6 给出了HSCAT-D 与ASCAT-C 风速偏差随SST 变化的关系，其中SST 数值范围为［-1，32］℃。由图6 可见，HSCAT-D/N4 风速约为7 m/s时SST 影响导致的风速偏差最为显著，幅度大于1.0 m/s；而HSCAT-D/N5 风速偏差随SST 变化的幅度小于0.1 m/s，即SST影响导致的风速偏差被准确校正。

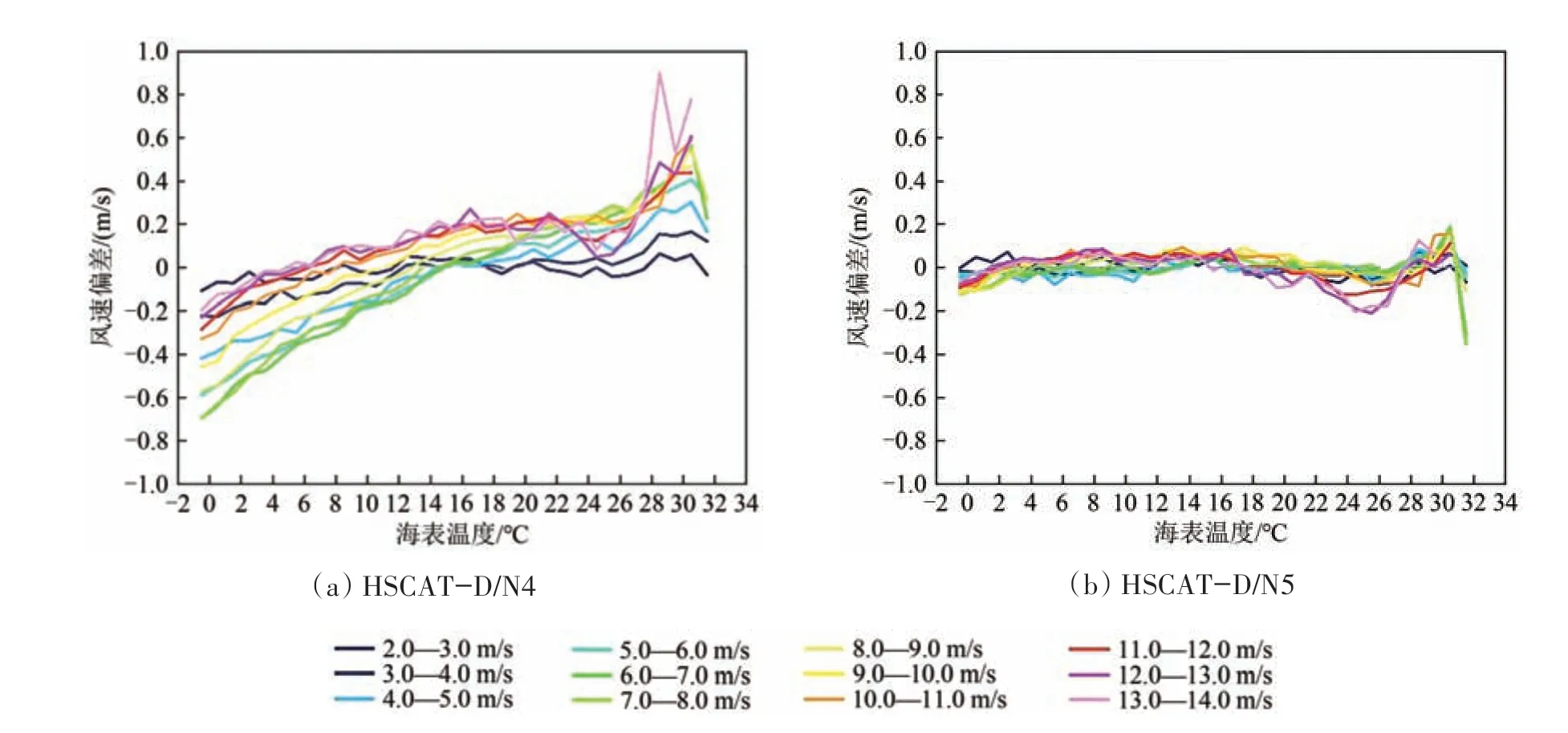
图6 HSCAT-D与ASCAT-C风速偏差随SST变化的关系Fig. 6 Wind speed biases between HSCAT-D and ASCAT-C as a function SST

由于SST 值大小与地理位置高度相关，使得HSCAT-D/N4 偏差也呈现出显著地理分布特点。图7 给出了HSCAT-D 与ASCAT-C 风速偏差的地理分布特点。由图7 可见，HSCAT-D/N4 风速在高纬度地区由于SST值较低而呈现风速负偏差。

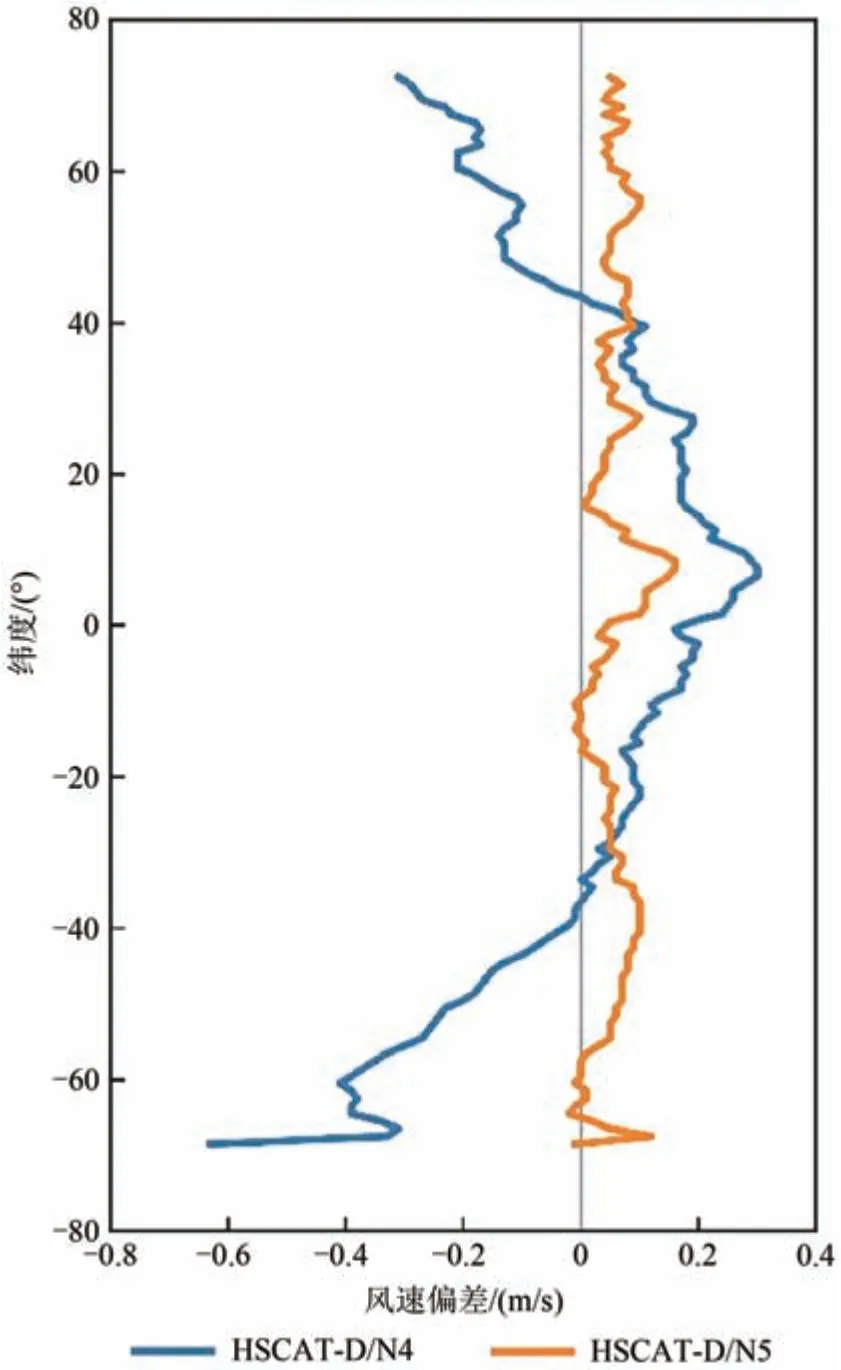
图7 HSCAT-D与ASCAT-C风速偏差随纬度变化的关系Fig.7 Wind speed biases between HSCAT-D and ASCAT-C as a function of latitude

4.3 HSCAT与ASCAT海面风场的总体比较

对HSCAT 与ASCAT 风速的整体一致性进行了对比分析，结果如表1所示。表1中风向RMS的计算中仅使用了风速（ASCAT 与HSCAT 的平均值）大于4 m/s 的数据。如表1 所示，使用NSCAT-5.HY-2 GMF 反演的HSCAT 海面风场与ASCAT 海面风场的一致性更好、HSCAT 海面风速与ASCAT 风速的一致性提高了约11%。HSCAT/N5 风速、U 分量和V 分量的方差显著减小。然而，风向RMS 改进幅度较小，认为这与风场反演算法有关。本研究中采用了多解反演算法和二维变分模糊解去除方法组合的风场反演方法，研究表明这种反演算法用于旋转扫描体制的散射计数据风场反演十分有效。

需要注意的是，表1中的对比结果与数据匹配条件有关。表1 中选用25 km 分辨率风场产品，配对数据的时间窗口为45 min。若时间窗口减小为20 min，则可得到ASCAT-C 与HSCAT-D/N5 风速的总体方差为0.47 m/s，风向RMS为9.2°。

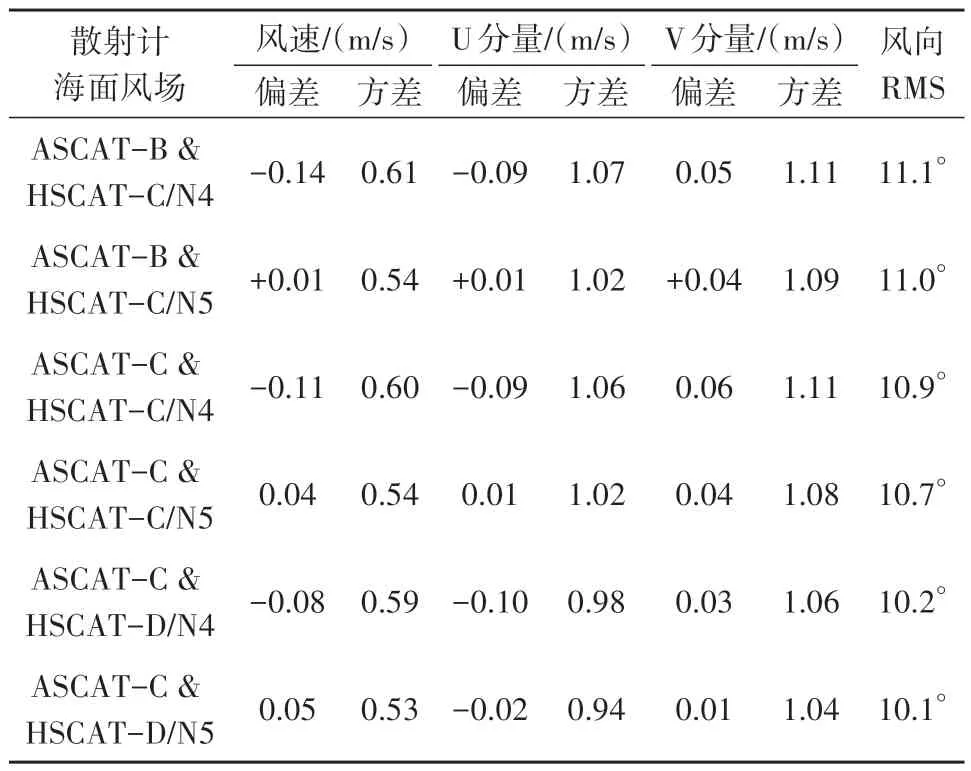
表1 HSCAT与ASCAT海面风场的对比结果Table 1 Overall wind comparisons between ASCAT and HSCAT

5 结 论

中国HY-2 系列B、C 和D 卫星搭载的微波散射计对全球海面风场形成了组网观测，也是当前和今后一段时期国内外海面风场遥感产品的最主要数据源。然而，目前用于风场反演的地球物理模式函数（NSCAT-4 GMF）存在显著误差，是影响HSCAT 海面风场反演质量的主要因素之一。本研究利用HY-2C 卫星倾斜轨道的特点，基于HSCAT-C 与欧洲C 波段ASCAT-B 产生的大量配对数据，通过改进NSCAT-4 GMF 中后向散射系数对风速和风向的依赖关系，并且补充了SST 因子项，最终构建了用于HSCAT散射计风场反演的NSCAT-5.HY-2 GMF。将基于NSCAT-5.HY-2 GMF 得到的HSCAT 风速与ASCAT 风速进行比较，结果表明两者的一致性得到显著提升，特别是HSCAT/N5反演风速的偏差不再依赖于SST变化。风速在25 m/s以内，各风速区间内HSCAT/N5 与ASCAT 风速的偏差小于0.1 m/s。

此外，中国Ku 波段中法海洋卫星散射计和FY-3E风场测量雷达（WindRAD）也面临现有GMF有待改进的问题；尽管本研究构建的NSCAT-5.HY-2 GMF 仅适用于HY-2 系列微波散射计，不具有普适性，但研究方法可推广到其他卫星微波散射计。

志 谢荷兰皇家气象研究所（KNMI）提供了本研究中的MetOp/ASCAT 和ECMWF 模式数据，在此表示衷心的感谢！