基于混合算法的多机器人协作任务均衡规划研究*

王喜敏，袁 杰

(新疆大学 电气工程学院，新疆 乌鲁木齐 830017)

0 引言

针对多机器人协作任务规划（Cooperative Multi-Robot Task Planning, CMRTP）问题，通过代价函数评价能够使任务规划结果获取较大的系统效能，但必须考虑任务规划结果的均衡性[1]，如果规划过程中某个机器人的任务量过于繁重，将出现任务规划失衡的情况，那么即使能够获取较大的整体效能，也会使部分机器人因任务量繁重而过早损坏，并且不利于系统整体执行效率的提高.所以在满足系统整体效能和移动机器人个体任务要求的基础上，考虑机器人任务规划的均衡性，尽量实现公平分配.机器人团队高效完成整体任务时，需要平衡各机器人的工作，只专注最小化总代价往往会导致劳动力失衡，所以在协作团队中满足总距离最小时，最小化所有机器人最大距离同样具有实际意义，否则会出现不正确的任务均衡效果.

现今对于CMRTP问题，熊衍捷等[2]为解决多通道资源负载均衡问题，提出基于NJW谱聚类的资源负载均衡调度算法，通过聚类划分一定的簇数量，进行加权的K-means算法完成聚类等方法提高负载均衡度，这促使我们应用一种简单的标准的聚类技术来解决多旅行商问题（Multiple Traveling Salesman Problem, MTSP）/均衡多机器人任务分配（Balanced Multi-Robot Task Allocation, BMRTA）问题.毛科技等[3]针对无线传感器网络的数据传输问题，提出能耗均衡的层次路由协议，通过划分不同规模的簇，实现网络能耗均衡.朱姗等[4]运用组合优化和聚类分析理论来缩短求解空间的方法，为大规模超市中的订单拆分问题提供了新思路.解决相关问题的同时提高求解效率，将不同算法进行融合来发挥算法的各自优势，克服或抑制各自的缺陷，实现算法优势互补.姚泽玮等[5]针对移动设备多边缘的负载均衡问题，提出粒子群遗传算法（Particle Swarm Optimization-Genetic Algorithm, PSO-GA）融合算法，通过任务调度来最小化边缘集合中最大的任务响应时间，缩短了边缘的任务响应时间并改善了用户体验.董亚倩等[6]在引导车选址中，利用调度最小生成树，解决任务均衡分配并优化了行进路径.罗海峰[7]设计一种局部搜索和大规模邻域搜索混合搜索的方法，利用局部搜索的局部性和大规模邻域的全局性，求解容量约束的车辆路由问题.胡士娟[8]、张硕航[9]等通过在杂草算法中引入繁殖机制产生的后代进行遗传操作，解决了工作量平衡的MTSP，从而改善快递员配送环节的任务平衡问题.Venkatesh等[10]在求解单仓库MTSP中，提出采用人工蜂群算法最小化所有旅行商的总距离，采用基于入侵杂草优化算法最小化所有旅行商所走的最大行驶距离.李道全等[11]考虑网络区域能耗的均衡问题，改进蚁群算法提高覆盖率和平衡网络能量的消耗.Bernardino等[12]提出一种分支切割算法与局部搜索结合的混合算法获得高质量的解.

本文在研究任务均衡规划问题时，将CMRTP问题表述为MTSP的一个复杂变体[13]，研究如何均衡机器人团队的所有机器人的行走距离，即如何最小化所有机器人的最长行走距离.为了能够达到任务均衡效果，对其聚类进行改进，将机器人总距离最小作为优化目标函数；在整体效能方面采用最小化最大路程作为目标函数.基于多种群智能的算法，使用黏菌算法和交叉操作相互结合来解决局部问题；结合头脑风暴优化算法思想以降低问题的复杂度和求解全局问题；利用最小化最大路径的方式求解任务规划问题的任务均衡问题.即不断地调整任务由哪个机器人完成，以及调整任务方案上完成任务的顺序.为了保证机器人系统完成任务之间的均衡性，使得每个机器人完成任务的代价尽量均衡，通过分析均衡度评价机器人团队的任务均衡性.本文分为两个阶段：第一阶段通过改进K-means聚类进行初步任务分配，第二阶段通过头脑风暴优化算法进行重规划、任务规划，获得较优的任务顺序方案，以便提高机器人利用效率和任务均衡性.

1 协作任务均衡规划问题分析与建模

多移动机器人协作任务规划问题中，存在机器人集合R={r1,r2,···,rm}，任务集合T ={t1,t2,···,tn}，任务ti的坐标(xti,yti)，任务子集合S ={S1,S2,···,Sm}，其中Sk(k=1,2,···,m)表示第k个机器人完成任务序列集合.C是一个N×N维代价矩阵，其中cij表示机器人从任务ti到tj的距离，同时规定c(ti,ti)=0，i ∈{1,2,···,n}表示相同任务之间的代价为0；c(ti,tj)=c(tj,ti)，i ∈{1,2,···,n}表示代价矩阵C为对称矩阵.

针对任务均衡规划问题，CMRTP问题考虑机器人工作均衡性，将其问题转为最小化所有机器人的最大距离更有实际意义.机器人位置、任务位置及从一个任务位置到另一个任务位置的代价矩阵是已知的.假设代价矩阵C是对称的，目标是规划任务和机器人，使得优化每个机器人完成任务的代价值较小和机器人完成任务代价之间均衡度较小.

1.1 优化目标

1）适应度值1.机器人集合完成任务所行走的总距离：

2）适应度值2.机器人行走的最长路程，目标函数为最小化最长距离：

其中：zk(k=1,2,···,m)为第k个机器人完成任务子集合Si(i=1,2,···,m)行走路程.

1.2 约束条件

针对任务均衡规划问题，任务和机器人需要满足以下约束条件.

其中：公式（6）和（7）表示约束所有机器人从集合出发点出发；公式（8）和（9）表示约束每个任务仅被机器人完成一次；公式（10）表示任务当前状态，任务完成情况；公式（11）和（12）表示机器人行走路线包含起始点；公式（13）、（14）和（15）表示任务间关系.

1.3 对多移动机器人系统的任务规划问题作如下假设

1）机器人工作的空间是二维平面；

2）机器人执行任务的成本代价用机器人行走的距离长度表示；

3）机器人在各自目标任务位置处执行任务消耗的代价忽略不计；

4）机器人从相同的集合点出发，且各机器人完成任务之后回到集合点.

2 算法介绍

黏菌算法[14]（Slime Mould Algorithm, SMA）是一种基于种群的新启发式算法，基于黏菌在自然界中的觅食行为，类似于细菌觅食优化算法[15].通过不断地移动和变化，筛选出通往食物的最短路径.Nakagaki等[16]发现黏菌在迷宫中觅食，自由移动形成觅食路径，即迷宫问题的最优解.利用SMA算法参数少、寻优效果强的优点，以解决网络流、线性规划、路由和运输等问题[17].

头脑风暴算法[18]（Brain Storm Optimization, BSO）与模仿生物遗传和觅食等群体行为的演化算法不同，模拟人类通过交流互动提出新方法的头脑风暴过程，能够在全局探索和局部开发之间达到较好平衡[19].本质是将不同知识背景的人聚集在一起，将具有同样或相似想法的人进行分组，选出各组的代表，在各组内部进行新想法讨论，是一种局部开发的过程；组间进行相互交流提出更广的新想法，是一种全局探索的过程.采用聚类[20]进行分组，在对应组空间内进行局部搜索获取局部最优值，在不同的组空间之间进行全局搜索获取全局最优值.

CMRTP问题中，执行任务的顺序是提高机器人系统执行效率的关键.第一阶段采用基于代价适应度值的改进K-means聚类技术进行任务分配.通过对代价适应度值进行聚类，不再局限于空间维度的限制，能够减少计算量.第二阶段采用了一种混合智能优化算法，基于SMA、BSO类内局部更新和类间全局更新个体方式、交叉操作和大规模邻域搜索操作进行更替方法，进行任务规划.

2.1 多机器人协作任务分配

任务分配的目标是根据机器人的使用情况，将任务集合通过分区、分组的方式分为不同区域，给机器人集合规划不同的任务子集合来完成任务.在给定任务空间维度{x1,x2,···,xn}，假设两个任务之间相似度可以通过其欧几里得度量来衡量，将相似点归为一类，同时将不相似的点区分开，首先需要假设类的个数k为已知的，并且同一个任务点只属于某一类.因此聚类的问题就是寻找k个不相交的非空集合{S1,S2,···,Sk}，且满足约束条件（公式(13)～(15)）.K-means算法目的是对所有任务点进行预处理，根据任务集合点的分布将任务分成m个簇，找出中心点作为优化算法的起始点，优化每个群.在这种情况下，该算法将一个大问题分解成几个子问题，并求出中心点，以降低问题的复杂度.

由于K-means传统思想是对数据点进行划分，即根据每个点的位置，k个节点作为聚类中心，计算每个节点与该中心节点距离，采用将节点分配到最近的中心点的思想进行划分，然而这样划分的结果导致划分不均匀，从而导致任务均衡性相对较低.为了保证多机器人完成任务过程中任务均衡，对任务区域内的任务成本代价适应度值进行聚类，这样能够减少问题的复杂度，如图1所示.

图1 适应度值聚类过程

步骤1：初始化任务集合、机器人集合、相关参数；

步骤2：随机生成初始种群，计算任务点之间的距离作为距离矩阵D（见式(1)）；

步骤3：在种群中随机选择m个个体作为聚类中心，并计算该m个聚类中心的适应度值1；

步骤4：计算种群中个体的适应度值1与m个聚类中心的适应度值取差值绝对值，选择差值绝对值最小的作为聚类中心，同时将当前个体归为此类；

步骤5：计算类中个体适应度值的平均值，将类中适应度值与平均值最接近的个体定为新的聚类中心；

步骤6：保证所有任务点分配到不同的类中，否则，重复步骤4.

2.2 多机器人协作任务重规划

针对所有任务是否完成以及是否获得合理的规划方案，对当前任务规划结果进行分析，判断当前任务规划方案的合理性和可行性.针对何时重规划以及如何重规划问题，本文采用任务和目标期望值判断依据解决任务重规划的选择问题.在头脑风暴优化算法中，对机器人内部任务进行大规模邻域搜索，开展任务局部重规划，获得局部最优值；对机器人之间的任务进行交叉操作搜索，开展任务全局重规划，获得全局最优值，以此解决重规划问题.任务重规划判断流程如图2所示.重规划过程如图3所示.

图2 任务重规划框图

图3 任务重规划过程

图3（a）中机器人内部当前规划方案存在均衡性较差问题，进行局部重规划获得较优规划方案.图3（b）中机器人之间当前规划方案存在均衡性较差问题，进行全局重规划获得较优规划方案.

3 多机器人协作任务均衡规划算法

为获得多移动机器人协作任务分配结果并保证所有机器人的任务均衡，每个机器人需要完成多个任务和优化路线方案.将CMRTP问题转化为MTSP模型求最优解，优化最小化机器人最长路程为最佳路线方案，使得每个机器人所走的距离都较短，从而得到总路径相对较小和每个机器人所走路程均衡，达到任务均衡效果，再通过均衡度、差异度、偏差率进行综合评价均衡效果优劣.

3.1 算法设计

1）种群初始化：初始种群通常是随机生成的，但是在保证个体多样性的前提下，不能同时获得较优的收敛速度，将会出现算法寻优速度慢的问题.所以本文将黏菌算法进行迭代生成的初始种群进行计算适应度值1，保留排序较优的个体作为初始种群，减少算法的寻优次数.

2）交叉算子：根据CMRTP问题的特点设计算法，有利于改善算法的性能.引入交叉算子产生尽可能多的新个体，提高搜索能力.交叉操作在机器人内部的交流是一种局部开发的过程，在机器人之间进行交流是一种全局探索的过程.交叉操作就是将亲代种群的个体片段进行选择性交换、匹配部分基因，产生新的高质量个体，如图4所示.

图4 交叉操作

3）大规模邻域搜索操作[21－22]：remove移除算子操作中随机选取移除的路线个数，在相邻的路线中移除i个任务，从当前解中选择一个任务i对任务进行初次排序，选择第一个点.采用repair算子操作能够得到不同类型的解，提高了解的质量.

4）扰动算子：采用随机个体聚类中心替换的策略，计算适应度值，比较更新当前个体.大规模邻域搜索操作对当前方案进行扰动操作，选择最优适应度值1作为最优方案.

3.2 算法实现

基于混合算法的多机器人协作任务均衡规划算法如图5所示.

图5 任务均衡规划算法

4 实验与分析

4.1 实验环境与参数设置

在Windows 10操作系统、Matlab2020a编程软件进行测试实验.每个实例运行20次以确保95%的置信区间，记录每个机器人的行走路线和行走距离.在不同机器人数量和任务数量下开展研究，通过均衡度、偏差率和差异度评估本文算法性能和任务规划效果.种群为50，迭代次数为600，概率参数为：z=0.03、Pone=0.5、Ptwo=1-Pone、Ponecenter=0.3、Ptwocenter=0.3、ωinitial=1、ωfinal=0.对遗传算法（Genetic Algorithm, GA）、蚁群算法[23－24]（Ant Colony Optimization, ACO）、SMA算法解决多机器人任务均衡规划问题的规划结果进行对比.

4.2 实例验证及结果

为验证所提算法的有效性，本文在TSPLIB国际标准测试库中，选取了三个不同规模的实例，采用不同算法验证规划结果的均衡性，记录相关数据并对实验结果进行具体分析和比较.实例中列举了不同实例和机器人数量的变化，如表1所示.

表1 测试实例

实例eil101中3、4、5、10个机器人的任务规划优化结果如图6所示.图6（a）代表机器人和任务分布，蓝色方格为机器人位置，红色圆圈为任务位置以及任务的序号.图6（b～e）为任务规划结果，不同颜色代表不同机器人的任务以及完成任务过程中机器人完成任务的顺序.

由图6（e）可知，不同机器人完成的任务之间没有出现重复现象，说明每个任务只被一个机器人完成，同时展示出任务规划后的最优方案.可以获得机器人分配的任务完成顺序、任务数量以及成本代价，如表2所示.

表2 实例eil101、机器人数量为10的任务规划结果

根据10个机器人完成对应任务所需成本代价分别为112.487 5、113.202 5、109.504 9、109.965 6、113.701 4、109.615 9、106.780 0、112.756 4、110.212 9、109.710 1，得出本文改进算法的平均均衡度为9.69%、平均差异度为2.848%、平均偏差率为1.997%.SMA算法的平均均衡度为14.059%、平均差异度为3.483%、平均偏差率为3.312%.经比较分析，本文算法任务均衡规划结果均衡度相对提高，机器人之间的成本代价差异程度相对较小，任务成本代价相对平衡，保证了机器人之间任务的均衡性，表明本文算法在均衡机器人任务代价上具有较好的均衡性.

4.3 算法性能分析

采用多个评估指标综合评价任务均衡规划结果的均衡性.机器人之间的行走距离的平均差异程度越小，其均衡性越好.SMA、GA、ACO和本文算法在不同实例上的任务规划结果、记录机器人行走最长距离的最优值（m）和平均值（m）如表3所示.SMA和本文算法任务规划结果的机器人团队总路径的最优值（m）和平均值（m）如表4所示.本文算法和SMA算法任务规划结果的平均偏差率PDav（%）、平均均衡度σ（%）和平均差异度CV（%）如表5所示.平均值[25]反映算法的平均优化精度，平均值越小证明算法的优化精度越好；最优值越小表示优化路径越短.平均均衡度σ和平均差异度CV 越小，说明机器人之间行走路径相近，任务成本代价差异程度相对较小，任务均衡性越优，任务规划效果就越好.平均偏差率PDav越小，表明任务规划结果的机器人总行走距离相对误差越小.

4.3.1 均衡性评估指标

1）任务均衡度：

其中：maxLi表示第i(i=1,2,···,m)个机器人的最长路程，minLj表示第j(j=1,2,···,m)个机器人的最短路程，i/=j，m为机器人总个数.

2）平均偏差率：

其中：平均长度为20次独立运行所得最优解的平均值，最优解是已知最优解.

3）路径长度平均差异度CV[26]反映各机器人路径长度的差异程度：

4.3.2 本文算法的收敛效果分析

为了验证本文算法的收敛效果，给出3个实例中不同机器人数量完成不同任务数量的规划结果，本文算法和黏菌算法迭代到全局最优值的收敛曲线，如图7所示.

图7 不同实例的迭代收敛曲线

图7（b）是实例eil101中机器人数量为4时的任务规划结果，收敛曲线的迭代早期为20时，本文算法约为195，而SMA算法约为200，前者起初找到全部最优值相对较优，所需要的迭代次数较少，收敛速度相对较快；本文算法寻得全局最优值为182.5，而SMA算法寻得全局最优值为184，精度提高约0.82%，可以得知本文算法在寻优精度方面效果较佳.图7（d）是实例eil101中机器人数量为10时的任务规划结果，本文算法在迭代次数100内寻得全局最优值，在较早的迭代过程寻得全局最优值为113.701 4，体现出较优的收敛速度，而SMA算法表现出陷入局部最优值的现象，寻得全局最优值为115.097 7，本文算法寻得全局最优值的精度提高约1.21%.综上所述，本文算法在不同实例中的搜索效率具有不同程度的提高，相对SMA算法，本文算法收敛效果较佳，全局搜索效果较好.本文算法的收敛曲线均位于SMA算法的下方，在算法收敛早期快速搜索到全局最优值的迭代次数相对较少、最优值精度相对较高.

由表3可知，比较不同实例中机器人任务规划的最长路径，本文混合算法的最优值比SMA算法解的质量高.不同实例中，本文算法收敛到全局最优值的过程中寻得全局最优值相对较优，而SMA算法迭代对应适应度值与本文算法比较显出最优解的劣势.通过表4进行综合分析，改进算法不论最长路径最优值还是团队最优值都有不同程度提高.表4中本文算法最优解以及平均解都比SMA算法的解的质量高.结合表5中平均均衡度σ、平均差异度CV、平均偏差率PDav指标，可知本文算法的机器人总行走距离相对误差小，保证了算法解的均衡.

表3 机器人任务规划最长距离

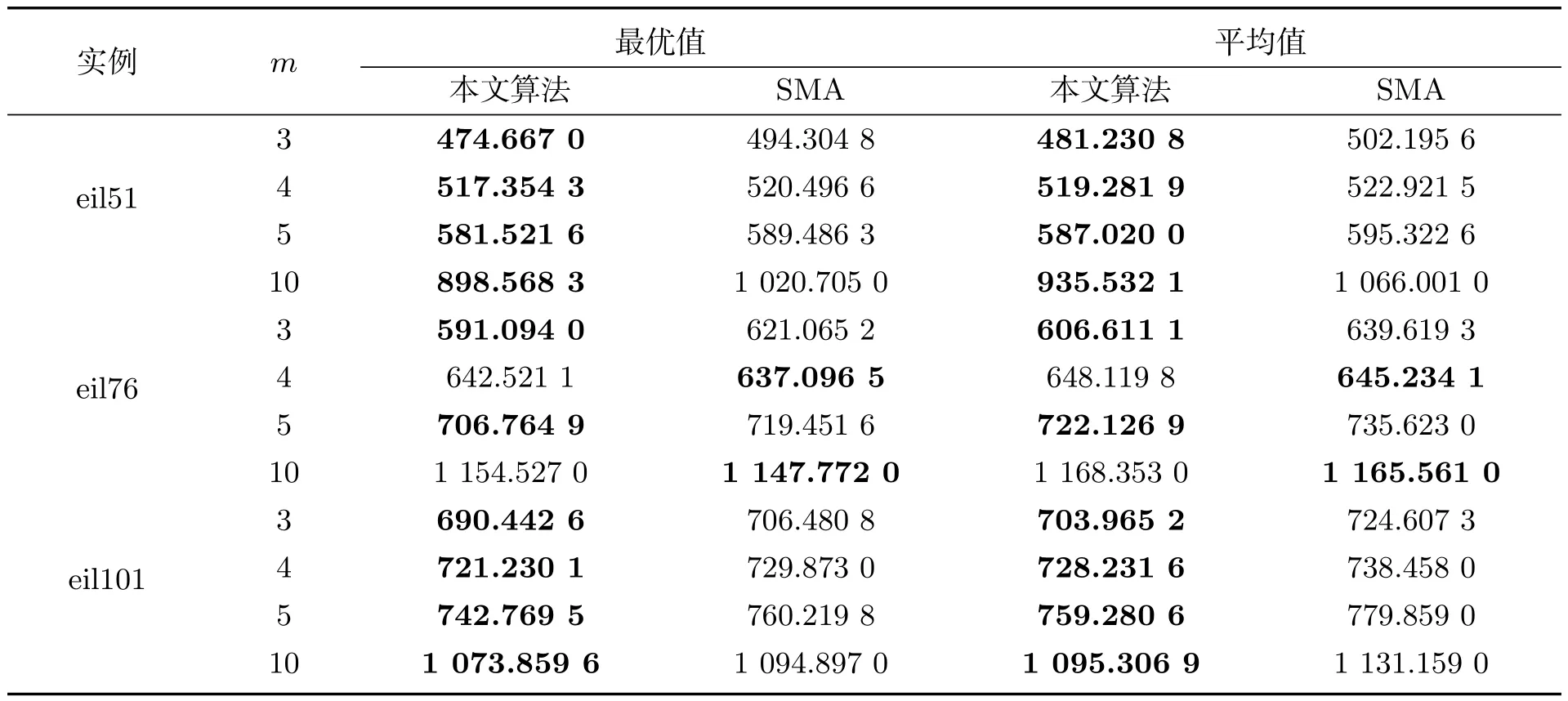
表4 机器人团队任务规划总路径

由表5可知，从平均均衡度σ分析，评估了最长行走距离和最短行走距离之间的差异，在任务数量较少安排机器人较少的情况下平均均衡度σ都在3%左右，机器人数量为5时，相对SMA算法提高了4%左右，均衡性相对较优；实例eil51-10中，机器人数量较多时平均σ在20%左右，本文算法在寻找最优任务规划效果上均衡性从31%降到28%，均衡性有所提高；实例eil101-10中，平均均衡度σ从14.059%降低到9.690%，最长行走距离和最短行走距离差距缩短，任务规划效果合理.从平均差异度CV 分析，评估了机器人团队中所有机器人行走距离之间的差异程度，很好地展现了机器人之间的差距，从不同实例得出本文算法在实例eil51-10中提高6%左右，其它情况下提高1%左右，将所有机器人之间的差异程度降到相对较低，本文算法的平均差异度CV 相比SMA算法更小，进一步保证了机器人之间良好的均衡性.从平均偏差率PDav分析，将所有机器人的整体效益进行对比，本文算法相比SMA算法具有更小的平均偏差率，说明更接近最优值，取得规划效果较佳.

表5 均衡性评估指标

SMA、GA、ACO、本文算法在不同实例中的任务规划结果和任务规划结果的机器人最大距离对比柱状图如图8所示；总距离对比柱状图如图9所示.图中不同颜色代表不同算法数据值：橘色柱形为GA、绿色柱形为ACO、紫色柱形为SMA、黄色柱形为本文算法.

图8 实例eil51、eil76和eil101不同算法最优值对比

图9 实例eil51、eil76和eil101不同算法总距离对比

由图8可知，黄色柱形的最大距离最优值最高点均位于其它算法的下方，说明比较后的最大距离相对较小，全局最优值相对较优，优化路线方案效果明显.

由图9可知，黄色柱形与其它颜色柱形进行比较，总距离整体较低，总距离值相对较小，体现出本文算法在全局搜索方面的优越性.可以看出本文算法的机器人最长距离最优解要比其它算法的最优解较优；获得机器人团队总距离也小于其它算法的值.综上所述，改进算法的寻优效果优于其它比较算法，任务规划结果较优.

4.3.3 任务规划结果的均衡性分析

为了验证任务均衡性能的好坏，获取本文算法在不同实例中的最优均衡规划结果的路程分布如图10所示.不同颜色代表任务规划中机器人的行走距离，进而计算每个机器人之间的行走距离的均衡度和路径长度平均差异度.

图10（a）代表实例eil51中机器人数量为3时，机器人1的行走路程为158.993 5，机器人2的行走路程为159.571 5，机器人3的行走路程为158.236 2，平均均衡度σ为1.874%，路径长度平均差异度CV 为0.540%，平均偏差率PDav为1.383%，机器人之间任务成本代价相对差异在2%以下，均衡效果与SMA算法相比有所提高.图10（b）代表机器人数量为10时的路径分布，平均均衡度σ为28.500%，路径长度平均差异度CV 为2.848%，平均均衡度大的原因是任务数量少的情况下安排的机器人数量多，使得出现总体规划效果差的现象，通过路径长度平均差异度CV 分析，本文算法的路径长度平均差异度为2.848%，而SMA算法相对较高，均衡效果劣于本文算法，本文算法任务规划结果相对合理.图10（c）代表实例eil101中机器人数量为10时，机器人1行走路程为112.487 5，机器人2行走路程为113.202 5，机器人3行走路程为109.504 9，机器人4行走路程为109.965 6，机器人5行走路程为113.701 4，机器人6行走路程为109.615 9，机器人7行走路程为106.780 0，机器人8行走路程为112.756 4，机器人9行走路程为110.212 9，机器人10行走路程为109.710 1，平均均衡度σ为9.690%，路径长度平均差异度CV 为2.848%，平均偏差率PDav为1.997%.SMA算法中平均均衡度为14.059%，路径长度平均差异度CV 为3.483%，平均偏差率PDav为3.312%，与本文算法比较相对较高，成本代价差异大，造成在机器人之间任务均衡效果不佳.

图10 实例eil51、eil101路径分布图

5 结论

在解决多移动机器人任务均衡规划问题中，为了使机器人的工作量相对接近，机器人之间任务均衡，同时提高机器人团体效益.本文在任务分配问题中采用基于适应度值的K-means聚类进行分类，减少了计算复杂度；利用黏菌算法三阶段搜索策略提高了求解问题的全局搜索能力，利用头脑风暴算法的机器人内进行局部更新操作和机器人间进行全局更新操作对任务子集合进行重规划，任务集合内进行任务规划，获取较优任务路线方案；采用交叉操作和大规模邻域搜索操作提高了该任务规划算法的全局搜索和局部搜索能力.实验结果表明：基于混合优化算法的任务均衡规划方法能够合理均衡规划多移动机器人系统中的任务和机器人，机器人之间的路径成本代价平均差异度相比SMA算法低，体现出成本代价之间的均衡效果较优，能实现多移动机器人的均衡规划，提升完成任务效率.所提出的算法在多移动机器人任务均衡规划问题中具有较好的均衡性.