基于POD-RBF方法的管道内壁几何识别*

余 波, 陶盈盈

(1. 合肥工业大学 土木与水利工程学院 工程力学系, 合肥 230009;2. 大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024)

0 引 言

天然气和石油是当今世界上重要的化石能源,管道运输是其主要的运输方式．由于长时间的运输,管道内部很容易发生腐蚀老化,进而导致管壁破裂和油气泄漏等灾难性事件的发生[1]．因此,管道缺陷检测对保证其运输安全尤为重要,识别管道内壁被腐蚀的几何形状对精准评估管道的腐蚀程度具有深刻的指导意义．

几何形状识别[2-4]主要通过系统外表面响应数据进行内部几何形状估算,属于反几何问题．近年来,多种无损检测技术[5-6]已被广泛应用于管道状况的评估,其中漏磁检测法[7]由于检测范围广、灵敏度高、适应性强以及零污染等优势备受关注．显然,准确快速地求解磁场正问题是确保几何形状高效识别的前提．在众多正问题数值求解方法中,有限元法因其强大的适应性和稳定性,迄今为止已被广泛地应用于求解磁场问题[8-10],并获得了准确的结果．因此,本文采用有限元法求解磁场的相关响应量,并以此为基础进行管道内壁几何形状的识别．

选用合适的优化方法是反几何问题成功的另一关键点,优化方法可分为局部搜索的梯度类优化算法和全局搜索的演化类优化算法．由于在几何形状识别过程中其形状会随迭代过程不断更新,从而对目标函数灵敏度的求解带来一定的困难,且灵敏度的求解在一定程度上会增加反演计算的成本．为避免灵敏度的计算并实现全局搜索的目标,本文选用非梯度类算法进行目标函数的优化．具有代表性的方法包括遗传算法[11]、布谷鸟搜索算法[12]、蚁群算法[13-14]、粒子群算法[15-16]和灰狼优化算法(grey wolf optimization, GWO)[17-18]等,其中GWO算法因其具有简单高效的优势而广受学者的关注．Mirjalili等[17]提出了GWO算法并将其应用于解决工程设计问题．Kohli等[19]将混沌理论引入到GWO算法中,以加快其全局收敛速度．文献[20]对目前GWO算法的相关改进及应用进行了总结,验证了该方法的可行性和有效性．基于此,本文选取GWO算法来实现管道内壁的几何形状识别．

在反演迭代过程中需多次实施正问题分析,尤其对于全局类演化搜索算法,调用正问题分析的次数或许可达成千上万次．此外,对于大型复杂模型,因其高维数和复杂性,直接进行分析相对困难且数值模拟耗时过长[21]．为此,对数值模型的规模或阶数进行有效的降阶处理就显得尤为重要．Hellström等[22]利用本征正交分解法(proper orthogonal decomposition, POD)进行了管道流动中结构的识别．Eftekhar Azam等[23]结合该方法和人工神经网络,提出了一种监督学习方法,并用于检测、定位和量化结构损伤强度．POD是预测响应最受欢迎的模型降阶方法之一,该方法以有限的数据捕获计算过程中的主要成分,可显著降低自由度,提升计算效率．但该方法的精度受样本数量与样本间相关性等因素的影响,样本的选择至关重要．利用本文建立的变几何样本库可有效处理这一难题．

常规POD的预测模型随着几何形状的改变需要反复更新有限元刚度矩阵,这在一定程度上严重增加了POD模型的计算成本．因此,探索一种代理模型以避免在计算过程中因几何改变反复求解有限元刚度矩阵是非常有必要的．常见的代理模型有多项式回归(polynomial regression, PR)[24-25]、Kriging(KRG)[26-27]、径向基函数(radial basis function, RBF)[28-30]和人工神经网络(artificial neural network, ANN)[31-32]等．其中,PR模型是通过样本数据基于最小二乘原理来拟合近似多项式．由于PR的模型简单、计算量小,且多项式的平滑能力能使带有噪声的函数快速收敛,因而成为最常用的代理模型之一．然而,PR在处理高度非线性问题时,由于高次多项式的使用会出现不稳定现象．KRG是对区域变量求无偏内插估计值的一种插值方法,预测精度主要依赖于初始采样,可能会导致模型过早停止或过于局部收敛．ANN是一种模拟人脑分析和处理信息方式的人工智能算法．该方法从复杂的数据中学习,确定输入和输出变量之间的关系,从而进行预测分析．RBF模型以关于Euclidean距离或者其他类似度量的函数为基函数[33-34],通过线性加权来插值拟合数据．Jin等[35]利用多种性能评价标准和14个标准测试函数系统地比较研究了PR、RBF和KRG等代理模型的性能,得出在处理不同阶数的非线性和问题规模时,RBF模型在准确性和稳定性等方面的表现最好．Jing等[36]提出了一种基于自适应RBF与遗传算法相结合的可靠性评估方法,以降低结构可靠性分析的计算成本．Liu等[37]针对多目标优化计算量大的问题,利用RBF提出一种基于自适应逼近模型的高效多目标优化方法,并通过算例验证了该方法的有效性和实用性．综上,若将POD和RBF的优势耦合,即可实现在降阶分析正问题的同时避免刚度矩阵的重复计算．例如,Khatir等[38]基于扩展等几何分析,将断裂力学试验与数值模型相结合,利用POD-RBF识别了板结构的单、多裂纹．Henneron等[39]应用该方法能够在合理的计算时间和良好的精度下得到有限元的近似解,从而模拟非线性静磁器件．Wang等[40]基于仿真结果,采用POD-RBF的降阶方法,预测了不同滑移幅值和不同微动磨损循环次数下试样的磨损特性．研究表明,POD-RBF可高效准确地预测相关响应量,显著地降低计算成本．截至目前,已出版的研究工作基本上是基于固定几何样本库采用POD-RBF进行响应量的预测．为此,本文基于构建的变几何样本库建立了POD-RBF降阶代理模型．该方法可期望在识别过程中避免因管道内壁几何形状的改变而需反复求解刚度矩阵,在满足拟合精度要求的前提下降低计算成本．

1 管道内部几何反演理论

1.1 静磁场二维有限元基本理论

本文在静磁场环境中进行管道内壁几何形状的识别,将其简化为平面问题,对应的平衡方程为[41]

(1)

其中x=(x,y),μr为相对磁导率,μ0为空气磁导率,Az为磁势,Jz为电流密度．

考虑两类边界条件:

(2)

如图1所示,Γ=Γ1∪Γ2表示域Ω的边界,m,n分别是Γ2和Γd的法向单位矢量,Bt为切向磁通密度．

图1 求解域示意图Fig. 1 The diagram of the solution domain

在磁导率不同的两种媒质界面Γd上,磁势应满足连续性条件:

(3)

对式(1)应用Galerkin有限元法可得

(4)

通过有限元离散可得

KAz=Jz,

(5)

其中K为总体刚度矩阵,Az为结点磁势向量,Jz为电流载荷向量．

不同管道内壁几何对应模型不同的表面磁势信息,其中管道内壁几何由若干个几何参数表示．在管道内壁识别过程中,通过有限元计算获得不同管道内壁几何相应的磁势信息,进而生成样本,并建立磁势数据与几何参数的关系．另外,利用管道内壁真实几何模型的磁势信息,对管道内壁几何形状进行预测．

1.2 本征正交分解-径向基函数

在采用POD-RBF求解之前,建立有效的样本库关系到问题的求解精度,因此选取合适的样本点至关重要．拉丁超立方抽样(Latin hypercube sampling, LHS)方法是目前使用较为广泛的抽样方法之一,该抽样方法利用分层的思想,保证样本点是从给定的设计空间内均匀随机抽取的．基于LHS生成POD-RBF降阶代理模型所需样本库的参数,有效避免了计算过程中因管道内壁几何形状改变反复更新刚度矩阵,能在保证计算精度的同时提高计算效率．

绝大部分工作均选用某个方向上的磁感应强度进行研究,我们期望从数值上建立全面反应有关磁感应强度信息的数据与模型几何的关系,故选用有限元分析中的磁势作为响应量．在相同边界条件下,通过LHS生成对应的不同管道内壁几何参数,进而利用有限元计算得到磁势样本矩阵:

ψ=[ζ(α1),ζ(α2),ζ(α3),…,ζ(αN)],

(6)

式中αi为控制管道内壁几何的参数,ζ(αi)为n维磁势列向量,N表示样本个数．

对样本矩阵ψ进行奇异值分解:

ψ=CSVT,

(7)

式中C∈Rn×n为ψ的左奇异向量组成的矩阵;V∈RN×N为ψ的右奇异向量组成的矩阵;S∈Rn×N仅在主对角线上有值,称为ψ的奇异值,可表示为si(i=1,2,…,min(n,N))．所有奇异值按降序排列,通过以下规则

(8)

实现k个奇异值和对应奇异向量的自适应截断进而可近似描述矩阵ψ,即

(9)

本文χ取99.999%．

(10)

(11)

其中i=1,2,…,N;q=1,2,…,k．

写成矩阵形式为

σ=WΦ,

(12)

其中W为wqj组成的矩阵,Φ可表示为

(13)

为了提升计算效率这里选用inverse multiquadtric(InvM)核函数对Φ进行近似展开,则Φ中任一元素φj(αi)可表示为

(14)

式中,c是取值大于零的平滑系数,rji表达式如下:

rji=‖αi-αj‖2,

(15)

‖αi‖2为αi的2范数．由式(12)可得

W=σΦ-1．

(16)

通过式(10)、(12)、(16)可得任意参数αp对应的磁势响应量:

(17)

由式(17)可以看出,通过变几何样本库的构建,在求解不同管道内壁几何对应磁势响应量时,只需更新几何对应的基函数向量Φ(αp),这将在很大程度上节省计算成本．

1.3 目标函数的优化

通过确定管道内壁几何参数αp即可确定管壁的几何形状,建立与αp有关的目标函数

(18)

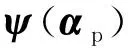
受灰狼群体捕食行为的启发,GWO算法被提出．灰狼被认为是食物链顶端的捕食者,大部分喜欢群居,一个群体平均有5～12只狼．在群体中,他们有着严格的等级制度,如图2所示,从高到底依次是首领狼a,副首领狼b,普通狼c和底层狼ω．

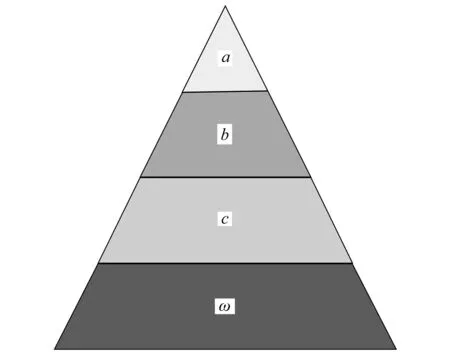
图2 灰狼的等级制度Fig. 2 The hierarchy of gray wolves

灰狼的狩猎是在首领狼a的带领下,进行围攻捕食．捕食过程分为三个阶段:

1) 通过气味跟踪、追逐、接近猎物;

2) 锁定猎物位置后,进行包围;

3) 快速地攻击猎物．

在狼群捕食过程中,围剿猎物公式为

C=|CXp(t)-X(t)|,

(19)

C=2ϑ1,

(20)

式中Xp(t)为猎物的位置,t是迭代步数,X(t)为灰狼的位置,ϑ1从[0,1]范围内随机取值．灰狼的位置更新如下:

X(t+1)=Xp(t)-BD,

(21)

在更新过程中,保留当前结果最好的前三组解,依次为a,b和c狼的位置．狼群中其他狼的位置根据a,b和c狼的位置进行更新:

(22)

(23)

通过式(22)、(23)不断更新前三个最优灰狼的位置,直到满足优化标准条件．

2 数 值 算 例

2.1 基于POD-RBF对响应量的预测

取管道任一横截面的附近区域进行分析,假定待识别的管道内壁几何分别为圆、椭圆和不规则形状．图3是该问题的简化模型,几何尺寸如图所示,其中方块被选为参考点(即后续算例中的测点),区域Ι、Ⅱ和Ⅲ分别为石油(或天然气)、管道壁和空气．在正方形上边界(y=1)处施加磁势Az=0.5 Wb/m,下边界(y=-1)处施加Az=0 Wb/m．天然气和石油由于抗磁性它们的相对磁导率和空气相近,即相对磁导率μr均取为1．管道材料选用常用的X52钢,对应的B-H取值参考文献[42]．

图3 圆型管道内壁Fig. 3 The inner wall of the circular pipeline

首先对POD-RBF模型的正确性进行验证,假定管道内壁形状为圆,该几何对应的参数αp里仅有一个元素,其值为0.533 m．样本对应的参数α通过LHS在0.5～0.6 m生成10组．用POD-RBF模型预测被对比点的磁势．有限元计算采用9 856个四节点四边形单元,10 037个节点,单元划分如图4所示,图5展示了相应磁场强度的大小．两种方法计算结果误差如图6所示．

图6(b)显示POD-RBF计算预测的响应量与有限元计算结果的最大相对误差不超过0.06%,即该算法对求解管道内部内壁几何正问题有效．

图4 有限元网格 图5 磁场强度大小Fig. 4 The FEM meshFig. 5 The magnetic field intensity

(a) 参考点磁势的绝对误差 (b) 参考点磁势的相对误差(a) Absolute errors of the magnetic potential at the reference points(b) Relative errors of the magnetic potential at the reference points图6 参考点磁势的误差Fig. 6 The magnetic potential errors at the reference points

2.2 不同样本数量对识别结果的影响

本小节对如图3所示管道内壁几何为圆的问题进行反演．利用LHS在0.5～0.6 m分别生成10组、20组和40组相应的几何参数α,再通过有限元分别建立N=10,20,40的样本库,进一步探究不同样本数量对反演结果的影响．

ε和tmax分别设定为10-10和100．从表 1对比分析的三组样本方案结果显示,不同数量的样本均能达到较高的识别精度．如图7和图8所示,当管道内壁形状为圆时,采用不同数量的样本,识别结果均在16步内收敛．使用40组样本时,经过6次迭代即可获得更准确的识别结果,但计算成本可能会随着样本数量的增加而增大．因此在复杂模型识别中,选择合适数量的样本至关重要．

图7 不同样本数量对应的目标函数值 图8 不同样本数量对应的几何参数 Fig. 7 Objective function values with different sample sizes Fig. 8 Geometric parameters with different sample sizes

表1 识别结果

为了确定后续算例的样本,采用继承LHS[43]生成样本,期望在保证精度的同时尽可能降低计算成本．经测试,后续分别拟采用50组和40组样本进行椭圆形和不规则形内壁几何的识别．

同时样本中对应的几何参数范围也会影响识别结果,接下来我们讨论在当前样本N=10下管壁几何的识别情况．待识别的真实管壁几何半径在0.45～0.69 m内,识别结果如表 2所示．

表2 不同方案下的识别结果

从表中可知,真实内壁几何在0.50～0.61 m间识别结果的相对误差均在1%内,在这范围外的相对误差随着半径的增大(或减小)而增加,当半径减小到0.45 m时,识别结果的相对误差达到了10.892 1%．综上,在有限的样本下,待识别的几何参数在所建立样本库相应的几何参数范围内识别结果更准确．但当样本库足够大时,理论上可以识别出任意管壁的几何．

2.3 基函数对反演结果的影响

如图9所示,本小节假定管道内壁形状为椭圆,真实几何对应的参数αp=[0.625,0.42]Tm．通过InvM核函数和紧支撑的四阶样条函数[44]讨论不同基函数对识别结果的影响．其中紧支撑的四阶样条函数可以表示为

图9 椭圆型管道内壁Fig. 9 The inner wall of the elliptical pipeline

(24)

样本对应的参数α由LHS在0.40～0.65 m生成50组．ε和tmax分别设定为10-8和300,两种方法的迭代初始值均设置在0.9～1.0 m之间．

如图10所示,使用紧支撑的四阶样条函数迭代总次数少于InvM核函数,且两种方法均能得到比较准确的几何．但在同样的步数下,InvM核函数耗时更短．同时为兼顾反演成本,在后续算例中选用InvM核函数．

(a) Inverse multiquadtric核函数(a) Inverse multiquadtric kernel functions

2.4 不同误差对反演结果的影响

为验证本文方法的抗噪性,本小节在测点响应上添加随机误差．算例采用如图11所示的模型,管道内壁的几何形状由12个参数控制,该组参数在平面内均匀分布,从0°～360°每隔θ=30°选取,最后通过样条曲线拟合成封闭图形．样本对应的参数α由LHS在0.5～0.6 m内生成40组, 真实几何对应的参数αp=[0.526,0.578,0.533,0.556,0.518,0.544,0.538,0.575,0.510,0.565,0.530,0.594]Tm．

图11 不规则几何形状的管道内壁Fig. 11 The inner wall of the pipeline with irregular geometry

考虑1%,2%和3%的随机误差,添加误差后的测点磁势可表示为

(25)

本算例假定ε和tmax分别为10-7和8 000．需要说明的是,有限元模型与POD-RBF降阶代理模型的计算结果是存在一定偏差的．

表 3列出了在不同误差水平下的参数识别结果．

图12直接展现了本文方法识别带有12个几何参数问题的性能．值得注意的是,在δ=0时,识别出的几何参数与真实参数存在微小差异,但拟合出的边界与真实边界几乎完全重合．从图13和图14可以看到,在误差水平分别为1%和2%时,识别结果与真实几何仍吻合较好．甚至δ=3%时,图15显示本文方法仍能识别出几何的基本轮廓．另外,从图16更能直观地观察到,在不同的误差水平下,本文方法可获得较为理想的磁势响应场和识别结果．

图12 δ=0时的识别结果 图13 δ=1%时的识别结果 Fig. 12 The identified results with δ=0Fig. 13 The identified results with δ=1%

图14 δ=2%时的识别结果 图15 δ=3%时的识别结果 Fig. 14 The identified results with δ=2%Fig. 15 The identified results with δ=3%

(a) 真实几何 (a) The true geometry

3 结 论

本文建立了变几何样本库的POD-RBF降阶代理模型,结合GWO算法构建了一种新型的管道内壁几何识别框架．通过LHS生成样本库后,利用POD-RBF对响应量进行预测,可避免迭代过程中因几何改变而反复更新刚度矩阵．GWO算法的引入实现了无需灵敏度计算的全局目标函数优化．数值算例表明,本文算法不仅能够准确预测正问题响应,同时可实现对管道内壁几何的准确识别．即使对于带有高维几何参数且考虑噪声问题,该算法仍具备强劲的识别性能,显示出了良好的识别稳定性．同时,本文的研究工作可为拓扑优化、几何识别和无损检测等变几何计算问题提供新思路．

致谢本文作者衷心感谢工业装备结构分析国家重点实验室开放基金(GZ21109)对本文的资助．