横向非均匀温度场作用的FGM夹层圆板热屈曲分析*

龚雪蓓, 赵伟东, 郭冬梅

(1. 青海大学 土木工程学院, 西宁 810016;2. 青海省建筑节能材料与工程安全重点实验室, 西宁 810016)

0 引 言

功能梯度材料(FGM)板壳通常是由陶瓷和金属两种组分材料沿厚度方向按照特定混合规则加工而成的一种新型梯度复合材料．与层压及纤维增强复合材料相比较,功能梯度材料能够明显减弱乃至消除不同组分材料之间的界面效应,从而有效解决因热膨胀失配和应力集中等不利因素导致材料失效的问题．陶瓷通常具有突出的耐高温性能和良好的抗腐蚀性能,金属通常具有优异的延展性和机械强度．由于陶瓷-金属FGM板壳结构兼具上述诸多优异性能,使其在诸如航空航天、热核反应、军事工业和化学工程等领域具有广阔的应用前景．

随着FGM板壳结构在现代工程领域的逐步应用,对其结构力学行为的研究吸引了诸多研究人员的注意．常见的分析方法有忽略横向剪切变形效应的经典理论和计及横向剪切变形效应的各种剪切理论．经典理论的数学形式简单、物理概念直观,但其分析精度稍显不足．剪切变形理论的结果更为精确,但其数学形式复杂、推导过程繁琐．基于经典板理论(CPT),Najafizadeh和Eslami[1]讨论了FGM圆板轴对称热屈曲问题,推导得到了一般形式的平衡方程和稳定方程,给出了用于预测FGM圆板临界屈曲温度的解析解．基于一阶剪切变形理论(FSDT),Reddy等[2]导出了一个考虑三维热传导方程耦合的FGM板壳热弹性边值问题,并借助有限元方法研究了FGM圆柱壳与板的动态热弹耦合响应．Shen[3]基于高阶剪切变形板理论(HSDT),考虑组分材料特性的温度依赖性,推导了功能梯度板的广义von Kármán大挠度方程,为FGM板壳的几何非线性分析奠定了基础．Van Do等[4]介绍了一种基于HSDT的横向剪切函数和基于径向点插值方法的精确、高效的无网格近似方法,分析了沿厚度具有不同温度分布的FGM板在边缘压缩荷载下的后屈曲响应．Ma等[5]基于von Kármán几何非线理论,针对FGM圆板在热机械荷载作用下的非线性弯曲和后屈曲行为开展研究,并使用数值打靶法求解了非线性耦合常微分方程边值问题．Zhang等[6]基于HSDT和物理中面概念,研究了弹性地基上FGM矩形板的热后屈曲响应．Lee等[7]针对弹性地基上的FGM板,考虑厚度拉伸效应,通过修正四变量板理论的位移场,提出了一种简单有效的高阶剪切变形理论．陈明飞等[8]基于平面应变理论,利用等几何有限元方法分析了弹性边界条件下面内功能梯度三角形板的面内振动特性．

与FGM板壳结构比较,由其发展得到的FGM夹层板壳结构,具有更为优异的阻热、防腐和力学性能．常见的FGM夹层板壳结构有两种类型,一种为FGM面层和均匀材料(陶瓷或金属)夹层连接而成的FGM夹层板壳结构(下文称此类结构为A类FGM夹层板壳结构),另一类为FGM夹层连接纯陶瓷和纯金属面层构成的FGM夹层板壳结构(下文称此类结构为B类FGM夹层板壳结构)．到目前为止,研究人员针对FGM夹层板壳结构力学行为的研究已得到了诸多研究成果．Shen等[9]基于HSDT,研究了考虑初始几何缺陷的A类FGM夹层板在不同热环境下的屈曲行为．Zenkour等[10]采用正弦剪切变形板理论推导了简支边A类FGM夹层矩形板的稳定性方程,对不同温度场条件下的控制方程进行了解析求解．Wang等[11]采用两步摄动法求解了置于弹性地基上的A类FGM夹层矩形板的控制方程．Alibeigloo[12]将广义微分求积法应用于沿径向的状态空间方程,形成半解析状态空间微分求积法,并使用这种半解析状态空间微分求积法对不同边界条件下的B类FGM夹层圆板进行了轴对称热弹性分析．Mahi等[13]基于FSDT对幂律型简支边A类FGM夹层矩形板进行静力分析．Li等[14]基于静力平衡法推导了B类FGM夹层板在横向分布荷载作用下的控制方程,研究了体积分数指数、厚度与边长比和层厚比对板弯曲特性的影响．Van Do等[15]提出了一种简单而精确的无网格逼近方法,在考虑初始几何缺陷的情况下对A、B类FGM夹层矩形板在边缘压力作用下的后屈曲行为进行了分析．

当幂律型FGM板壳或夹层板壳沿厚度方向存在温差时,沿厚度方向的Fourier热传导温度场存在无穷级数形式的解．数值计算时需要截取级数的多少项才能获得精度可接受的解呢?据笔者文献调阅所知,到目前为止,该问题仍未被研究人员充分关注．Zhao[16]针对幂律型FGM圆板,考察了截取的级数项数目对解的精度的影响,获得了一些有意义的结果．本文针对夹紧边的B类幂律型FGM夹层圆板,考虑沿厚度非均匀温度场作用,基于层间连续性条件,给出了沿厚度方向的温度场分布函数的解析解,建立了基于经典板理论的轴对称几何非线性位移型控制方程与其边界条件(两点边值问题)．本文首先将非线性边值问题退化为关于挠度的四阶线性边值问题,通过分析线性特征值问题,得到了系统的有量纲临界屈曲温度差解析解．然后运用数值打靶法求解非线性边值问题,求解时截取级数的前97项进行计算,得到了精度很好的热过屈曲平衡路径和平衡构形数值解,并进行了参数影响分析．当模型退化为FGM板时,通过识别屈曲平衡路径上分支点的值和用解析公式计算得到的系统的有量纲临界屈曲温度差,均能与已有文献结果很好一致．

1 基 本 方 程

如图1所示的FGM夹层圆板,半径为a;总厚度为h;hc,hF和hm分别为纯陶瓷层、FGM夹层和纯金属层的厚度．为便于分析,建立圆柱坐标系(Orθz),坐标轴正向如图所示．其中rOθ坐标面位于圆板中面内,坐标原点位于圆板中面形心处．中面内任意点(r,θ,0)处的径向、环向和横向位移分别由U(r,θ)(与r轴正向一致为正)、V(r,θ)(与θ轴正向一致为正)和W(r,θ)(与z轴正向一致为正)表示．

1.1 几何方程

在轴对称情况下,圆板中面任意点(r,θ,0)处横向位移W和径向位移U都是径向坐标r的一元函数,即W=W(r),U=U(r),环向位移V恒等于0．基于von Kármán几何非线性板理论,圆板内任意一点(r,θ,z)的应变-位移关系为[17]

(1)

式中(·),r代表(·)对r的一阶导数．

1.2 物理方程

在轴对称情况下,考虑温度应力,FGM夹层圆板的本构关系[18]表达为

(2)

式中T(z)表示圆板中任意点(r,θ,z)处相对初始无应力状态温度(即参考温度)的变温值,为厚度坐标z的一元函数;E(z)和α(z)分别是圆板中任意点(r,θ,z)处材料的等效弹性模量和等效热膨胀系数;μ是Poisson比,本文假定为常数．

为得到FGM夹层板壳结构坐标z处的温度应力,需要求解如下的一维Fourier热传导边值问题[19]:

(3)

式中K(z)是圆板中任意点(r,θ,z)处材料的等效导热系数;Tl和Tu分别表示FGM夹层圆板金属侧表面和陶瓷侧表面相对参考温度的变温值,用ΔT=Tu-Tl表示夹层圆板两表面之间的温度差．为了物理概念直观,本文建模过程使用Tl,Tu和ΔT作为系统的热荷载参数．需要指出的是,当金属侧表面温度相对参考温度不变化时(即Tl=0 ℃),陶瓷侧的变温值Tu即为两表面温度差(即ΔT=Tu),本文热过屈曲数值解就是在这种情况下得到的．

假设FGM层材料体积分数为幂律分布[16],即

Vc(z)=(0.5+z/hF)k,Vm(z)=1-Vc(z), -hF/2≤z≤hF/2,

(4)

式中Vc和Vm分别指陶瓷和金属组分材料的体积分数,非负指数k为梯度指数．

则FGM材料层坐标z处的材料等效弹性模量E(z)、等效热膨胀系数α(z)和等效导热系数K(z)可表示为厚度坐标z的函数[20]:

E(z)=Emψ1(ξ),α(z)=αmψ2(ξ),K(z)=Kmψ3(ξ),

(5)

式中Em,αm和Km分别为金属组分(与金属面层材料相同)材料的弹性模量、热膨胀系数和导热系数．

ψi(ξ)是无量纲坐标ξ(ξ=z/hF)的连续函数,其数学表达式为

ψi(ξ)=1+ηi(0.5+ξ)k,i=1,2,3,

(6)

式中ηi=ri-1,r1=Ec/Em,r2=αc/αm,r3=Kc/Km,其中Ec,αc和Kc分别为陶瓷组分材料(与陶瓷面层材料相同)的弹性模量、热膨胀系数和导热系数．

本文所用组分材料特性[16]如表1所示．

表1 金属和陶瓷组分的材料特性

将式(6)取i=3代入式(5)中的第三式,再将式(5)中的第三式代入式(3),考虑K(z)=Km(-hm-hF/2≤z≤-hF/2),K(z)=Kc(hF/2≤z≤hF/2+hc)与温度场边界条件和连续性条件,解边值问题(3)得到如下温度场分布函数:

(7)

式中Tc=[hcATl+(hF+hmB)Tu]/(hF+hcA+hmB)为FGM夹层纯陶瓷侧相对参考温度的变温值,Tm=[hmBTu+(hF+hcA)Tl]/(hF+hcA+hmB)为FGM夹层纯金属侧相对参考温度的变温值,ΔT=Tu-Tl为圆板上下表面温度差,无量纲系数A,B分别为

在轴对称变形情况下,FGM夹层圆板的薄膜力和弯曲内力为

(8)

将式(1)、(5)、(7)代入式(2),再将式(2)代入式(8),得内力/内矩表达式如下:

(9)

(10)

(11)

(12)

刚度系数Si由下式计算:

(13)

NT和MT分别为热膜力和热弯矩,可由下式计算:

(14)

将式(5)中的第一式代入式(13),通过积分运算得到刚度系数Si:

Si=Amhiχi,i=0,1,2,

(15)

式中Am=Emh/(1-μ2)是均质金属圆板的抗拉刚度,无量纲系数χi为

(16)

(17)

(18)

将式(5)的第一、第二式和式(7)代入式(14)得

(NT,MT)=-(1+μ)AmαmTl(ζ0,hζ1),

(19)

无量纲系数ζi(i=0,1)的表达式为

(20)

(21)

无量纲系数βi通过下式计算:

(22)

式中

(23)

η4=r4-1,r4=Tc/Tm,N为非负整数．

将式(6)(i=1,2)和式(23)代入式(22),得βi的表达式为

(24)

(25)

1.3 平衡方程

轴对称情况下,功能梯度夹层圆板的平衡微分方程为

(rNr),r-Nθ=0,

(26)

(rMr),rr-Mθ,r+(rNrW,r),r+qr=0,

(27)

其中q为横向均匀分布荷载,与z轴正向一致为正．

2 边 值 问 题

2.1 控制方程

为便于数值计算,引入下列无量纲变量:

其中x为无量纲径向坐标变量,w,u分别为圆板中面上任意一点的横向和径向无量纲位移,λ为相对参考温度的无量纲变温,Q为无量纲横向均布荷载．

将式(9)—(12)代入式(26)、(27),考虑前述无量纲变换关系,得到一组无量纲位移型几何非线性常微分控制方程如下:

(28)

(29)

式中∇2(·)=(·),x/x+(·),xx,(·)x表示关于x的一阶导数．

2.2 边界条件

不可移夹紧边界条件为

w(1)=0,w,x(1)=0,u(1)=0;

(30)

中心对称条件为

(31)

3 线性特征值分析

我们已经知道,周边夹紧的FGM夹层圆板的热屈曲属于分岔屈曲问题．结构的临界屈曲温度差可以通过识别结构热过屈曲平衡路径上的分岔点对应的值来确定,也可以通过求解线性特征值问题得到．考虑到分岔点对应的变形是微小的,因此忽略非线性控制方程中的径向位移函数u及其各阶导数与全部非线性项,得到一个关于挠度w的四阶线性微分方程如下:

∇4w+λ∇2w=0．

(32)

方程式(32)与边界条件式(30)中的前二式和中心对称条件式(31)中的前二式构成一个线性特征值问题．通过求解该特征值问题,可以得到无量纲临界屈曲温度λcr(即特征值)．考虑到工程设计人员对该系统的最低临界屈曲温度(即最小特征值)更感兴趣,而最小特征值对应于圆板的一阶轴对称屈曲的分岔点解,因此,为了得到最小特征值,可以假设一个圆板中心挠度有限的一元挠度函数如下:

(33)

式中J0为零阶Bessel函数,C1和C2为积分常数．

将式(33)代入边界条件式(30)中的前二式,得到如下齐次线性代数方程组:

(34)

式中J0,x代表J0对x的一阶导数．

在屈曲状态下,积分常数C1和C2不全为零,根据Cramer法则,线性代数方程式(34)的系数矩阵的行列式必然为零,再考虑到最小特征值λ≠0,因此有

(35)

根据著名的Bessel函数关系,有

(36)

式中J1为一阶Bessel函数．

对式(36),当x=1时,考虑式(35),有

(37)

基于式(37),可以得到系统最小的特征值为

λcr=14.684．

(38)

根据式(38),再结合前文给出的无量纲温度与有量纲温度变换关系,对于具有实际参数的不可移夹紧边FGM夹层圆板,当金属侧表面相对初始参考温度变温值为Tl时,系统的有量纲临界屈曲温度(Tu)cr为

(39)

(40)

(41)

在式(39)的基础上,可进一步定义有量纲临界屈曲温度差如下:

(42)

由式(42)易见,系统的临界屈曲温度差不但依赖于系统本身的几何物理参数、梯度指数和所截取的级数项数目,也与变温值Tl有关．需要说明的是,本文仅针对Tl=0 ℃的情况进行计算,故系统的临界屈曲温度差在数值上等于使系统发生临界屈曲时陶瓷侧表面的温升值．换句话说,当Tl=0 ℃时,用式(39)计算得到的(Tu)cr和用式(42)计算得到的ΔTcr在数值上是相等的．另外需要指出,式(39)和式(42)经退化,可用于梯度材料圆板和均匀材料圆板的分析计算．

4 热过屈曲分析

控制方程(28)、(29)与边界条件(30)和中心对称条件(31)构成几何非线性常微分方程两点边值问题,可以用其考察固定边FGM夹层圆板在轴对称热机械荷载作用下的几何非线性力学行为．当横向荷载Q充分小时,可以用其考察系统的热过屈曲问题．限于篇幅,本文仅运用上述非线性边值问题讨论系统的热过屈曲问题,并进行相应的参数影响分析．考虑到模型属于几何非线性两点边值问题,因此本文运用数值打靶法对其求解．

4.1 打靶法求解简单说明

为了用打靶法求解上述两点边值问题,现假设[21]

Y=[y1y2y3y4y5y6]T=[ww′w″w‴uu′]T．

(43)

考虑方程(28)、(29)和中心对称条件式(31)中的第二式在x=0处具有奇异性,数值计算时,可在区间[Δx,1]上(本文计算时取Δx=10-4)计算．为了运用打靶法求解,需将原两点边值问题转化为以下初值问题:

(44)

式中φi(i=1,2)可从方程(28)和(29)中得到．

由于位移函数在x=0处连续可微,当Δx足够小时,可以用x=Δx处的值替代x=0处的值,即在x=0处的中心对称条件可表示如下:

Y(Δx)=[V10V2-V2/x0V3]T,

(45)

式中ζ为x=Δx处的初始挠度(赋值);Vi(i=1,2,3)为待定参数,由x=1处的边界条件确定．以上是本文数值求解过程中对打靶法使用方法的简单说明,有关打靶法数值求解方法更为详细的介绍和具体实现步骤和程序可以参阅文献[22-23]．

4.2 结果验证

将本文FGM夹层圆板退化为FGM圆板,考虑沿厚度非均匀温度场作用(取温度级数解前7项计算),在金属侧表面相对参考温度未发生变温(即Tl=0 ℃)的情况下,表2给出了不同厚径比和不同梯度指数的FGM圆板临界屈曲温度差ΔTcr(从识别过屈曲平衡路径上分岔点处的值和用式(42)进行计算两种途径得到),表中同时给出了文献[24]的结果．可以看出,本文结果与文献结果几乎一致．

表2 具有不同厚径比和梯度指数的FGM圆板在Tl=0 ℃时对应的临界屈曲温度差ΔTcr

4.3 热过屈曲分析

我们已经知道,当幂律型功能梯度板两侧存在温度差时,其沿厚度方向的温度场函数可以表达为无穷级数．由于级数收敛慢,需要取相当多项才能获得精度可接受的解[16]．在给定层厚比为2∶1∶2、底面温度相对参考温度不改变(即Tl=0 ℃)、梯度指数k=1和厚径比h/a=0.05的情况下,图2给出了一组不同的温度级数项数N对应的FGM夹层圆板(固定边界)的热过屈曲平衡路径．其中N=0为对应级数的前两项的计算结果,此种情况下沿板厚的温度场退化成了线性温度场．由图2可以判断,当幂律型梯度夹层板/壳在两表面之间存在温度差时,如果将沿厚度的温度场退化为线性温度场,数值解会严重失真．当N≥1时,沿梯度层厚度方向的温度场为非线性温度场,沿均质面层依然为线性温度分布．从图中可以看出,当N=95时(对应级数的前97项),数值解收敛到了一个很理想的程度．因此对于两表面存在温差的FGM夹层圆板,为了保证解具有足够的精度,除非特别说明,本文数值结果均为对应级数前97项的结果．

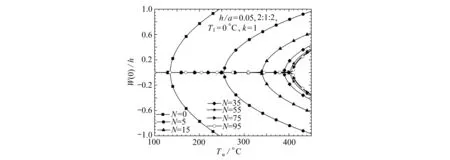
图2 不同的温度级数项数目对应的FGM夹层圆板热屈曲平衡路径Fig. 2 Thermal buckling equilibrium paths of FGM sandwich circular plates corresponding to different numbers of temperature series terms

为了考察厚径比对FGM夹层圆板热过屈曲平衡路径的影响,在给定层厚比为2∶1∶2、底面相对参考温度的温升Tl=0 ℃、梯度指数k=1的情况下,针对一组不同的厚径比h/a,图3给出了固定边的FGM夹层圆板的一组热过屈曲平衡路径．从图中可以看出,随着厚径比的增加,板的临界屈曲温度差ΔTcr增加．因为当厚径比h/a增加时,板的弯曲刚度随之增大,结构抗屈曲能力增加,该现象与定性结论一致．

图3 厚径比对FGM夹层圆板的热过屈曲图4 梯度指数对FGM夹层圆板的热过屈曲 平衡路径的影响 平衡路径的影响 Fig. 3 Effects of thickness-radius ratios on thermal Fig. 4 Effects of gradient indexes on thermal postbuckling equilibrium paths of FGM postbuckling equilibrium paths of FGM sandwich circular plates sandwich circular plates

为了考察梯度指数k对FGM夹层圆板热过屈曲平衡路径的影响, 在给定厚径比h/a=0.05、层厚比为 2∶1∶2、 底面温升Tl=0 ℃的情况下,图4给出了多个梯度指数k对应的FGM夹层圆板的热过屈曲平衡路径．从图可以看出,临界屈曲温度ΔTcr随着k的增加而增大,这里再次表明,对于层厚比为2∶1∶2的FGM夹层圆板,当梯度指数k增加时,结构抵抗热屈曲的能力是增加的．另外可以看出,随着梯度指数k的增加,其对于临界屈曲温度差ΔTcr的影响逐渐减小,这是因为当梯度指数k较小时,k对组分材料体积分数的影响更为显著,而随着k的增加,其对组分材料体积分数的影响逐渐减小．

为了考察层厚比对FGM夹层圆板热过屈曲平衡路径的影响,图5给出了不同层厚比对应的FGM夹层圆板的热过屈曲平衡路径．从图中可以看出,在厚径比h/a、梯度指数k和底面相对参考温度的温升Tl给定的情况下,随着梯度层相对厚度的增加,临界屈曲温度ΔTcr增加．

给定半径a=120 mm、梯度指数k=1、底面温升Tl=0 ℃、上表面温升Tu=480 ℃和层厚比为1∶2∶1的情况下,图6给出了不同厚度的FGM夹层圆板的热过屈曲平衡构形．可以看出,厚度h越小,过屈曲变形越大,该现象与预期结果一致．

给定半径a=120 mm、厚度h=6 mm、梯度指数k=1、底面温升Tl=0 ℃、上表面温升Tu=480 ℃时,图7给出了不同层厚比下FGM夹层圆板的热过屈曲平衡构形．从图中可以看出,在厚度和半径给定的情况下,梯度层相对厚度越小,FGM夹层圆板后屈曲变形越大．该现象表明,在FGM夹层圆板半径和厚度不变的情况下,通过改变层厚比,就可以显著改变FGM夹层圆板后屈曲变形程度,为工程中的弹性元件和结构设计提供了重要参考信息．

图7 不同层厚比的FGM夹层圆板的热过屈曲平衡构形 图8 不同梯度指数的FGM夹层圆板的热过屈曲平衡构形Fig. 7 Thermal postbuckling equilibrium configurations Fig. 8 Thermal postbuckling equilibrium configurations of FGM sandwich circular plates with different of FGM sandwich circular plates with different layer-thickness ratios gradient indices

给定半径a=120 mm、厚度h=6 mm、 底面温升Tl=0 ℃、上表面温升Tu=480 ℃和层厚比为1∶2∶1的情况下,图8给出了不同梯度指数对应的FGM夹层圆板的热过屈曲平衡构形．从图中可以看出,梯度指数k越小,FGM夹层圆板后屈曲变形越大．该现象表明,在FGM夹层圆板半径、厚度以及层厚比不变的情况下,通过调整FGM层的梯度指数,可以显著改变FGM夹层圆板后屈曲变形程度,同样为工程中的弹性元件和结构设计提供了重要的参考信息．

5 结 论

本文基于经典板理论,详细考察了横向非均匀温度场作用的边界夹紧的幂律型FGM夹层圆板的临界屈曲温度差和热过屈曲特性,得到了如下主要结论:

给定层厚比和梯度指数,随厚径比的增加,FGM夹层圆板的临界屈曲温度差单调增加．给定层厚比和厚径比,随梯度指数的增加,FGM夹层圆板的临界屈曲温度差单调增加．给定厚径比和梯度指数,随FGM层相对厚度的增加,FGM夹层圆板的临界屈曲温度差单调增加．给定半径和厚度,随着面板相对厚度增加,FGM夹层圆板的热过屈曲变形显著增加;随着梯度指数减小,FGM夹层圆板的热过屈曲变形显著增加．