图形化薄膜等效弹性模量的声表面波表征研究*

陈 龙, 肖 夏, 张 立, 戚海洋

(1. 天津大学 微电子学院, 天津 300072;2. 浙江省计量科学研究院, 杭州 310063)

0 引 言

芯片高度集成化和功能复杂化的需求促使应用于集成电路的材料、结构以及制造工艺不断改进和创新．低介电常数(low-k)材料的成功应用有效缓解了后端布线中寄生电阻、电容引起的互连延迟和信号串扰等问题[1-2]．相比于二氧化硅,low-k材料质软的特点[3-4]导致图形化互连薄膜整体机械性能恶化,严重影响互连系统稳定性．Cu/low-k互连薄膜普遍存在多孔较脆的特点,传统化学机械抛光(CMP)工艺由于较高的抛光压力不可避免地会对互连薄膜造成损伤．因此,为了开发适用于图形化薄膜、低压力的化学抛光技术,对图形化薄膜机械特性进行定量表征具有重要意义．

在过去的几十年中,研究者们已经提出并开发了用于测量薄膜机械性能的许多方法,如纳米压痕法[5-6]、膨胀实验法[7]、Brillouin光散射法[8]、原子力显微镜法[9-10]等．尽管不同检测方法都能够为大多数情况提供令人称道的解决方案,但它们在特定问题上存在一些局限性和缺点．以传统纳米压痕法为例,压头在压入薄膜时会破坏薄膜结构,这是一种有损检测．另一个缺点是其测量结果容易受基底和尺寸效应影响而出现较大误差．激光激发超声表面波技术是一种非接触式的无损检测方法,完全不受基底材料影响．声表面波在分层结构中传播时发生频散现象,高频和低频声表面波分别携带薄膜和基底信息[11]．基于此原理,声表面波技术在无损检测领域得到了广泛应用,它可以准确检测表面和亚表面缺陷[12-13],表征薄膜材料、功能梯度材料以及非均匀材料等力学特性[14-18]．近年来,声表面波技术也被应用于医学检测领域[19-20]．

现有的声表面波检测技术主要面向全部由low-k材料构成的匀质薄膜,而Cu/low-k图形化互连薄膜并非表现为各向同性．对于由两种或两种以上材料组成的复合材料,其宏观力学性能通常取决于细观组分的力学性能和分布方式,近几年来一直是广泛研究的课题．崔春丽等[21]基于广义自洽法,同时采用Gurtin-Murdoch界面模型和界面相模型研究了纳米纤维复合材料的有效弹性性能,获得了两种模型下有效体积模量的封闭解析解和计算有效面内剪切模量数值解的全部公式．陈海玉等[22]建立了细观等效模型,利用扭转变形、细观夹杂理论、弹性等效思想和M-T模型方法,推导了多成分组成的再生混凝土的宏观力学参数预测模型．

准确表征图形化薄膜的机械特性对于调整CMP工艺参数和保证互连结构稳定性有重要研究价值．本文采用横观各向同性和正交各向异性模型分别表征单大马士革和双大马士革薄膜结构,详细推导了声表面波在双大马士革薄膜/硅基底结构中的理论方程,使用有限元方法获得仿真频散曲线,并进一步与理论曲线匹配得到等效弹性模量．对比能量法计算结果发现,相对误差均低于5%,证明了声表面波方法表征图形化薄膜机械性能的可行性．

1 理 论 推 导

1.1 图形化互连薄膜等效结构模型

因此,通过下式可以建立等效体和代表性体积单元间的关系:

(1)

现在考虑一种简单的应力应变分布情况,第i层内的应力分量表示为

(2)

应变分量为

(3)

式中,txi,tyi,txyi和ezi,eyzi,exzi是每层介质中的附加应力和应变．

将式(2)代入式(1)中,可得附加应力满足以下条件:

∑φitxi=0, ∑φityi=0, ∑φitxyi=0,

(4)

式中,φi=hi/l,hi是第i层介质厚度,l为等效体厚度．同理,将式(3)代入式(1)中,得到附加应变条件:

∑φiezi=0, ∑φieyzi=0, ∑φiexzi=0．

(5)

对于所有层均为正交各向异性弹性体,则第i层的应力应变关系满足

ε=Dσ,

(6)

由式(4)和(5)消去式(6)中的附加应力和应变,得到等效工程常数表达式:

(7)

式中

1.1.1 单大马士革薄膜等效结构

图2为单大马士革结构,由金属互连线和low-k介质材料构成,将其看作互连布线层中的一个代表性体积单元．并做如下假定:1) 两种材料均为各向同性线弹性材料,互连线和介质的弹性模量分别为E1和E2,Poisson比分别为ν1和ν2; 2) 两种材料界面具有完美的黏附性,无相对滑动; 3) 材料的层理面相互平行．基于上述假定,单大马士革结构的等效工程常数为

图2 单大马士革结构代表体积单元Fig. 2 The representative volume unit of the single damascene structure

(8)

式中

计算结果表明,单大马士革结构可以等效为横观各向同性结构,而且弹性对称轴(x轴)垂直于分层介质交界面,坐标面yoz与各向同性面平行,共有5个独立的弹性常数,根据弹性常数与工程常数之间的转换关系得

(9)

1.1.2 双大马士革薄膜等效结构

图3为双大马士革结构代表体积单元,其中w1,h1为通孔的宽度和高度;w2,h2为引线沟槽的宽度和高度;T为结构单元的周期．求解其等效参数分为两步,首先将结构分为上下两层,上层由沟槽和填充介质构成,下层由通孔和介质构成,由于材料假定为各向同性,因此上下两层均可以等效为横观各向同性结构;在计算出每层的等效弹性常数后,再将其看成平行于xoy平面的层状复合模型计算．双大马士革结构表现为正交各向异性,共有9个独立的等效弹性常数:

图3 双大马士革结构代表体积单元Fig. 3 The representative volume unit of the dual damascene structure

(10)

1.2 表面波在图形化薄膜/硅衬底分层结构中的传播特性

非压电媒质中的波动方程和解的形式为

(11)

uj=αjexp(ikbx3)exp[ik(l1x1+l2x2+l3x3-vt)],

(12)

式中,ρ为介质密度;uj为微元介质沿xj方向的微小位移;cijkl为材料弹性刚度常数;αj为表面波各谐波分量的相对振幅;k为波矢的大小;b表示与传播方向垂直平面中波的振幅和相位随传播深度的变化;(l1,l2,l3)为传播方向余弦;v是表面波相速度．

将式(12)代入式(11)得到表面波在介质中传播的基本方程——Christoffel方程:

(Γjk-ρv2δjk)αk=0,

(13)

式中,δjk为Dirac δ函数,Γjk为Christoffel系数,Γjk=lillcijkl．图形化薄膜的Christoffel系数为

(14)

为确保式(13)存在非零解,其系数行列式必须为零:

(15)

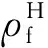
图4为表面波在双大马士革薄膜/硅衬底结构中的传播示意图,x3=0平面是薄膜和衬底交界面,x3=hf平面是自由表面,考虑波沿x1方向传播．

图4 表面波在双大马士革薄膜/硅衬底结构中的传播Fig. 4 The schematic diagram of SAWs propagating in the dual damascene film/substrate

因此要获得表面波传播特性与薄膜/衬底材料之间的关系,需要分别求解薄膜和衬底中的波动方程,且方程解还要满足以下边界条件:

1) 交界面处(x3=0)位移连续

(16)

2) 交界面处(x3=0)应力连续

(17)

3) 自由表面处(x3=hf)应力为零

(18)

其中

(19)

为满足边界条件,将薄膜和基底中的解线性组合,在薄膜中:

(20)

在基底中:

(21)

将式(20)和(21)代入式(16)—(19)中,可得边界条件矩阵:

M=[M1M2M3],

(22)

其中

式中,上标( )中的数字和字母分别表示薄膜和基底相关参量．令M的行列式等于零解得传播向量k,根据f=kv/(2π)可求得声表面波在双大马士革薄膜/基底中的色散曲线．对于单大马士革薄膜,根据式(9)先简化上述Christoffel系数和边界矩阵再求解色散曲线．因此,当表面波在图形化薄膜/衬底分层结构中传播时,相速度可以表示为

(23)

表1 双大马士革薄膜参数(参数标记见图3)和对应编号

以下讨论中,假设图形化薄膜淀积在硅衬底上,硅的密度为ρs=2.33 g/cm3,弹性常数为c11=165.7 GPa,c12=63.9 GPa,c44=79.6 GPa．声表面波沿Si[100]晶向传播,即方向余弦为l1=1,l2=0,l3=0．图形化薄膜由Cu和low-k材料构成,弹性模量分别为130 GPa和10 GPa,Poisson比分别为0.32和0.25,密度分别为8.9 g/cm3和1.0 g/cm3．

图5为表1结构对应的声表面波理论频散曲线．结果显示:在频率较低时,表面波可以穿透薄膜进入衬底,因此所有曲线在频率为零时的相速度近似等于Si[100]晶向的传播速度4 917 m/s[25]．随着频率增加出现正常色散现象,直观表现为曲线开始向下弯曲,而且随着沟槽宽度增加,SAW的色散现象愈发明显．编号②～⑩代表的图形化薄膜色散曲线随着频率增加彼此分离,且一直处于Cu和low-k曲线之间,曲线与两种材料占比成良好的线性关系,即在相同频率下,薄膜中low-k占比越大,其表面波速度越大．

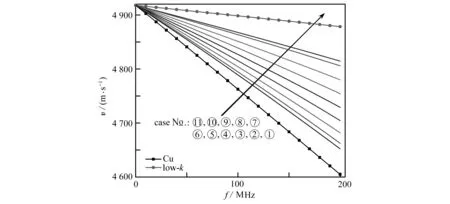
图5 膜厚为300 nm下表面波在表1的不同图形化薄膜中沿Si[100]晶向传播的色散曲线Fig. 5 Dispersion curves of surface acoustic waves propagating along the Si[100] direction in different patterned films in table 1 with a film thickness of 300 nm

2 数值算例及讨论

2.1 图形化薄膜/衬底结构的有限元仿真

本小节通过有限元仿真验证上述理论模型的合理性和准确性,选择固体力学中的特征值问题[26-27]模拟声表面波在图形化薄膜/衬底结构中的传播情况．由于在实际实验中采取的线光源只激发出x和z方向存在振动分量的“脊波”形式的应力波,因此在有限元软件中建立二维模型可以有效缩减计算量,节省时间．模型如图6所示,详细描述如下:模型宽度设置为一个波长,并在结构左右两侧增加周期性边界条件进一步简化模型加快计算速度,由于表面波沿介质传播时在到达表面下方深度1～2个波长后几乎衰减为零,因此衬底高度设置为3个波长,并在模型底部增加固定边界条件,薄膜表面设定为自由表面边界．

图6 图形化薄膜/硅衬底有限元网格化模型Fig. 6 The finite element meshing model for the patterned film/silicon substrate

图6为建立的有限元模型,对所建模型(表1编号⑥)采用模态分析求解特征频率f,如图7所示,波长为480 μm,位移幅度朝着衬底下方延伸逐渐减弱,最终衰减为零,完全符合表面波特点．对称和反对称模态对应两个特征频率的平均值作为最终频率,即10.23 MHz,因此该频率下的表面波速度为 4 910.40 m/s．声表面波相速度为vSAW=λf,调整表面波的波长即可得到表2中的参数,进一步使用多项式拟合可以得到仿真色散曲线．将仿真曲线与理论色散曲线簇匹配,通过最小二乘法确定等效弹性模量值．

(a) 对称模态 (b) 反对称模态(a) The symmetric mode (b) The antisymmetric mode图7 模型的表面振型及特征频率Fig. 7 The surface modes and eigenfrequencies of the model

表2 仿真模型的波长-频率-速度值

图8为表1中编号⑥结构的表面波色散曲线,等效弹性模量分别取10 GPa,15 GPa,20 GPa,25 GPa和30 GPa．图中显示随着频率增加,同一图形化结构的不同等效弹性模量会对频散曲线产生影响．具体表现为在相同的频率下,等效弹性模量越低的薄膜,声表面波的相速度衰减越快,曲线斜率越大．仿真曲线最接近等效弹性模量为20 GPa的理论曲线,精确匹配后得到其等效弹性模量Ef为18.74 GPa．由于薄膜厚度也是影响频散曲线的一个参量,图9所示为表面波沿Si[100]晶向传播时,图形化薄膜厚度对色散关系的影响．计算时选取单大马士革薄膜(VCu∶Vlow-k=1∶3),膜厚分别取50 nm,100 nm,200 nm,300 nm,500 nm和1 000 nm．图中显示在相同的频率下,薄膜厚度越大表面波传播速度衰减越快．因此在条件允许的情况下,增加薄膜淀积厚度可以增大色散曲线的曲率,有助于提高测量精度．本文综合考虑集成电路布线结构的研发挑战和需求,后文选择100 nm作为研究的薄膜厚度．

图8 膜厚为300 nm下表面波在表1编号⑥对应双大马士革 图9 表面波沿Si[100]晶向传播时单大马士革薄膜 薄膜中沿Si[100]晶向传播的理论和仿真色散曲线 (表4编号⑤)厚度对色散关系的影响Fig. 8 Theoretical and simulated dispersion curves of surface Fig. 9 Influences of the single damascene film thickness acoustic waves propagating along the Si[100] direction (case ⑤ in table 4) on the dispersion relation for the in the dual damascene film corresponding to case ⑥ in surface wave propagating along the Si[100] direction table 1 with a film thickness of 300 nm

2.2 能量法验证

能量法[28]可以同时考虑细观和宏观两种尺度推导得到复合材料的等效性能．等效体的应力和应变分别等于图形化结构的平均应力和应变,结构应变能为

(24)

式中,V代表结构体积;Ω为不同材料所占区域;σij和εij分别为应力与应变．假定结构沿x方向的正应变为1,其他方向为0时,应变能可以表示为

(25)

结果表明图形化薄膜等效弹性模量随Cu材料占比增加而增大,这一现象是符合实际物理规律的．值得注意的是,当Cu体积占比达到薄膜90%时,等效弹性模量为63.50 GPa,大约为Cu材料(130 GPa)的二分之一,表明由于low-k材料的存在,导致Cu/low-k图形化薄膜整体机械性能恶化．横向对比两表匹配结果,可以发现等效弹性模量还与薄膜具体结构相关．以表3中编号⑩为例,其体积比(VCu∶Vlow-k=1.9∶1)位于表4编号⑦(VCu∶Vlow-k=1∶1)和表4编号⑧(VCu∶Vlow-k=2∶1)之间,但等效弹性模量(47.74 GPa)并不在21.79 GPa和30.52 GPa之间,其他相同情况在表3中用黑体标明．因此,材料组分和具体结构均为影响薄膜等效弹性模量的因素,在相同体积比情况下,双大马士革结构普遍具有比单大马士革结构更高的机械强度,随着low-k材料的减少,这种规律体现愈发明显．声表面波法测量双大马士革和单大马士革薄膜的相对误差均在5%以内,最大相对误差分别为3.90%和4.25%,平均相对误差分别为2.06%和2.27%．因此在误差允许范围内表面波法可以用于表征图形化薄膜机械特性．

表3 双大马士革薄膜(hf=300 nm)等效弹性模量匹配结果

表4 单大马士革薄膜(hf=100 nm)等效弹性模量匹配结果

3 结 论

本文结合分层材料等效弹性性质理论、超声表面波理论和有限元仿真完成了图形化薄膜机械特性的量化表征．研究结果表明:在考虑互连材料均为各向同性时,单大马士革薄膜可以等效为横观各向同性结构,且弹性对称轴垂直于组分材料的交界面;双大马士革薄膜可以视为不同单大马士革薄膜在厚度方向的双层叠加,并最终等效为正交各向异性结构．本文基于声表面波方法对图形化薄膜的表征解决了现有表面波技术只能测量同种材料参数的问题,多个数值算例的匹配结果均有较高的准确率,研究结果对于选择low-k材料和发展化学机械抛光工艺具有重要指导意义．考虑目前low-k材料在制备过程中通过引入孔隙进一步降低介电常数的情况,未来将进一步细致研究孔隙结构及分布对多孔low-k介质与金属引线图形化集成结构的机械特性．