具有随机扰动和不确定性的中立型耦合神经网络有限时间同步*

2023-05-15王柯杰陈巧玉童东兵

应用数学和力学 2023年4期

王柯杰, 陈巧玉, 童东兵, 毛琦

(上海工程技术大学电子电气工程学院, 上海 201620)

0 引言

神经网络是模仿神经元信息传递过程所构建出的一种数学模型,可以用来解决一些复杂的非线性问题．近年来,神经网络已经被应用于生物信号检测、价格预测、风险评估和故障诊断等许多领域．随着研究的不断深入,中立型神经网络吸引了越来越多的关注．它是神经网络的特殊形式,其时滞在系统现在的状态和状态的导数中同时存在,由此导致该类系统具有更加复杂的动态行为,也使得此类系统相较于一般时滞系统具有更好的普适性．像化学反应过程、涡轮喷气发动机的转动过程等都可以利用中立型时滞系统进行建模．通过设计新的Lyapunov泛函和提出新的分析技巧,文献[1]研究了一类具有混合时滞的中立型耦合神经网络的指数同步．文献[2]利用M矩阵方法和随机分析法,研究了具有Markov切换参数的中立型随机神经网络的自适应同步．基于Lyapunov稳定性理论和不等式技术,文献[3]针对一类具有多时滞的中立型神经网络,研究了其平衡点的存在性、唯一性和全局渐近稳定性．

同步是指复杂网络中节点达到相同状态的行为,它不仅是一种基本的自然现象,也是复杂网络科学领域的重要研究方向之一．在过去的几十年里,学者们进行了全面的研究,并取得了大量的成果．其中,有限时间同步由于其优异的暂态性能而受到越来越多的关注[4]．文献[5]利用M矩阵方法得到了具有Markov拓扑和分布脉冲效应的神经网络有限时间同步判据．针对一类模糊中立型耦合Rayleigh系统,文献[6]利用有限时间稳定性理论和不等式技术,给出了其有限时间同步判据．对于具有自适应状态耦合的多权重复杂网络,文献[7]通过Lyapunov稳定性理论,设计出合适的控制器,使其达到有限时间同步和H∞同步．

在神经网络中,不确定性和随机扰动往往会造成不稳定或抖振,这些因素不利于神经网络的实际应用．因此对不确定时滞系统的研究一直是控制理论研究中的难点和热点问题之一．本文研究了具有不确定性和随机扰动的中立型耦合神经网络有限时间同步问题,所构建的系统模型与文献[8-10]相比引入了不确定性和随机扰动,更具实际意义．在Lyapunov稳定性理论的基础上,结合不等式技术,推导出中立型耦合神经网络有限时间同步准则．为了解决不确定性和随机扰动造成的问题,本文构造了合适的状态反馈控制器来保证主从系统实现有限时间同步．以Kronecker积形式给出有限时间同步判据,易于使用MATLAB工具箱来检验．

1 问题描述

考虑一类具有时滞和不确定性及扰动的中立型神经网络,其驱动系统设计如下:

d[xi(t)-Dxi(t-τ)]=[-(C+ΔC)xi(t)+(A+ΔA)f(xi(t))+

(B+ΔB)f(xi(t-τ))]dt,i=1,2,…,N,

(1)

其中,xi(t)=[xi1(t),…,xin(t)]T∈n代表第i个节点的状态向量,D=diag[d1,…,dn]且|di|<1,C=diag[c1,…,cn]是正定对角矩阵,A∈n×n和B∈n×n分别为连接权矩阵和时滞连接权矩阵,f(·)是神经元激活函数且有界,τ代表所考虑的时滞,未知矩阵ΔC,ΔA,ΔB代表系统参数的不确定部分．

其响应系统为

(2)

其中,系统参数D,C,A,B,ΔC,ΔA,ΔB的定义与式(1)相同,yi(t)=[yi1(t),…,yin(t)]T∈n,ui(t)为响应网络第i个节点的控制输入,c代表耦合强度,Γ=diag[γ1,…,γn]为内耦合配置矩阵,σi:+×n×n→n是噪声强度函数,ωi(t)=[ωi1(t),…,ωin(t)]T是定义在完备概率空间的标准Brown运动,G=(gij)N×N是外耦合转置矩阵,满足

将同步误差信号定义为ei(t)=col{ei1(t),ei2(t),…,ein(t)}=yi(t)-xi(t)．根据矩阵G的性质,可得到

(3)

其中

误差系统的耦合结构如图1所示．

图1 系统耦合结构图Fig. 1 The coupling structure diagram for the error system

通过使用Kronecker积,可以将式(3)改写为

d[e(t)-(IN⊗D)e(t-τ)]=

[-(IN⊗C)e(t)-(IN⊗ΔC)e(t)+(IN⊗A)F(e(t))+

(IN⊗ΔA)F(e(t))+(IN⊗B)F(e(t-τ))+(IN⊗ΔB)F(e(t-τ))+

(cG⊗Γ)e(t)+u(t)]dt+σ(t,e(t),e(t-τ))dω(t),

(4)

其中

σ(t,e(t),e(t-τ))=diag[σ1(t,e1(t),e1(t-τ)),…,σN(t,eN(t),eN(t-τ))]．

误差系统系统(4)中的控制器可以被设计如下:

u(t)=-R1e(t)+R2e(t-τ)-

ηsign(e(t)-(IN⊗D)e(t-τ))|e(t)-(IN⊗D)e(t-τ)|δ,

(5)

为了得到主要成果,则以下假设、引理和定义需要被提供．

假设1 噪声强度矩阵σ(·,·,·)是有界的,存在两个已知矩阵M∈n×n,N∈n×n,满足

tr(σT(t,e(t),e(t-τ))σ(t,e(t),e(t-τ)))≤eT(t)MTMe(t)+eT(t-τ)NTNe(t-τ)．

假设2 神经元激活函数f(· )是有界的,且对于任意xij,yij∈,满足下列条件:

注1 在实际系统中,许多常用的神经元激活函数满足假设2．例如Hopfield神经网络[11]中常用的f(x)=1/(1+e-λx),f(x)=(1-e-λx)/(1+e-λx)(λ>0)和f(x)=tanh(x);细胞神经网络[12]中常用的f(x)=(|x+1|-|x-1|)/2等．

假设3 未知矩阵ΔC,ΔA,ΔB满足下列结构:

(ΔC,ΔA,ΔB)=PS(t)(H1,H2,H3),

(6)

其中P,H1,H2和H3是已知的实矩阵,不确定矩阵S(t)可以是时变不固定的,且满足

ST(t)S(t)≤I．

(7)

注2 式(6)和(7)中的参数不确定性结构广泛应用于不确定系统的随机过程．式(7)可以对具有参数不确定性的实际系统进行精确建模．值得注意的是, 式(6)中的可变矩阵S(t)甚至可以是状态相关的, 即只要满足式(7),则S(t)=S(t,φ(t))成立．

引理1[13]存在x,y∈n,对任意ε>0,不等式xTy+yTx≤εxTx+ε-1yTy成立．

引理2[14]假设存在xi∈n,i=1,…n,0<ξ≤1,则下列不等式成立:

引理3[15]存在非负的连续函数χ(t)∈n,常数ζ∈(0,∞)和ξ∈(0,1)满足

Lχ(t)≤-ζχξ(t),t∈n0},

则χ(t)的平凡零解在概率空间内是有限时间稳定的,且随机设定时间满足E{T0}≤χ1-ξ(0)/(ζ(1-ξ))．

定义1[16]假设存在任意常数T0∈(0,∞)满足

则误差系统(4)可以实现有限时间同步,其中t≥t0+T0,且T0为同步的设定时间．

2 主要定理及证明

在这一节中,我们将推导出主从系统实现有限时间同步的判据．

定理1 在假设1、2、3满足的前提下,对于任意εi>0(i=1,2,…,10),对称矩阵R1,R2满足

(8)

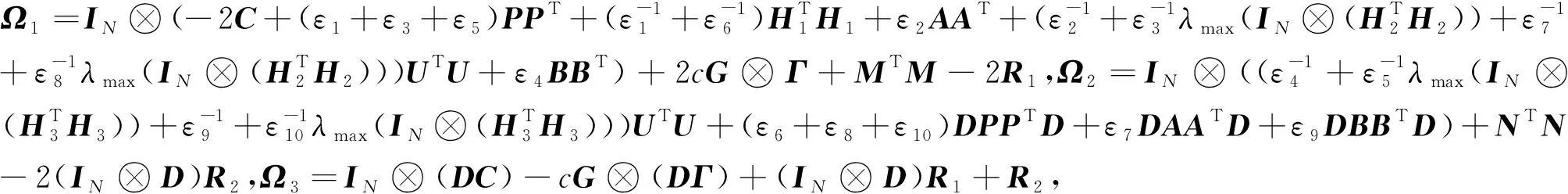
证明定义一个算子De(t)=e(t)-(IN⊗D)e(t-τ),并构造如下Lyapunov函数:

V(t)=(De(t))T(De(t))．

(9)

dV(t)=LV(t)+2(De(t))Tσ(t,e(t),e(t-τ))dω(t),

(10)

其中

LV(t)=2[(De(t))T[-(IN⊗C)e(t)-(IN⊗ΔC)e(t)+(IN⊗A)F(e(t))+

(IN⊗ΔA)F(e(t))+(IN⊗B)F(e(t-τ))+(IN⊗ΔB)F(e(t-τ))+

(cG⊗Γ)e(t)+u(t)]]+tr(σT(t,e(t),e(t-τ))σ(t,e(t),e(t-τ)))．

(11)

根据假设1和假设3,将控制器(5)代入式(11),能够获得

LV(t)≤-2eT(t)(IN⊗C)e(t)-2eT(t)(IN⊗ΔC)e(t)+2eT(t)(IN⊗A)F(e(t))+

2eT(t)(IN⊗ΔA)F(e(t))+2eT(t)(IN⊗B)F(e(t-τ))+

2eT(t)(IN⊗ΔB)F(e(t-τ))+2eT(t)(cG⊗Γ)e(t)-2eT(t)R1e(t)+

2eT(t)R2e(t-τ)-2ηeT(t)sign(e(t)-(IN⊗D)e(t-τ))×

|e(t)-(IN⊗D)e(t-τ)|δ+2eT(t-τ)(IN⊗(DC))e(t)+

2eT(t-τ)(IN⊗(DΔC))e(t)-2eT(t-τ)(IN⊗(DA))F(e(t))-

2eT(t-τ)(IN⊗(DΔA))F(e(t))-2eT(t-τ)(IN⊗(DB))F(e(t-τ))-

2eT(t-τ)(IN⊗(DΔB))F(e(t-τ))-2eT(t-τ)(cG⊗(DΓ))e(t)+

2eT(t-τ)(IN⊗D)R1e(t)-2eT(t-τ)(IN⊗D)R2e(t-τ)+

2ηeT(t-τ)(IN⊗D)sign(e(t)-(IN⊗D)e(t-τ))|e(t)-(IN⊗D)e(t-τ)|δ+

eT(t)MTMe(t)+eT(t-τ)NTNe(t-τ)．

(12)

根据假设2,可以得到

(13)

且

(14)

其中

由式(14),能够获得

eT(t)(IN⊗(UTU))e(t)．

(15)

通过假设3和引理1,有

-2eT(t)(IN⊗ΔC)e(t)=

-2eT(t)(IN⊗(PS(t)H1))e(t)=

-2eT(t)(IN⊗P)(IN⊗(S(t)H1))e(t)≤

(16)

2eT(t)(IN⊗A)F(e(t))≤

(17)

2eT(t)(IN⊗ΔA)F(e(t))=

2eT(t)(IN⊗(PS(t)H2))F(e(t))=

2eT(t)(IN⊗P)(IN⊗(S(t)H2))F(e(t))≤

(18)

2eT(t)(IN⊗B)F(e(t-τ))≤

(19)

2eT(t)(IN⊗ΔB)F(e(t-τ))=

2eT(t)(IN⊗(PS(t)H3))F(e(t-τ))=

2eT(t)(IN⊗P)(IN⊗(S(t)H3))F(e(t-τ))≤

ε5eT(t)(IN⊗(PPT))e(t)+

(20)

2eT(t-τ)(IN⊗(DΔC))e(t)=

2eT(t-τ)(IN⊗(DPS(t)H1))e(t)=

2eT(t-τ)(IN⊗(DP))(IN⊗(S(t)H1))e(t)≤

(21)

-2eT(t-τ)(IN⊗(DA))F(e(t))≤

(22)

-2eT(t-τ)(IN⊗(DΔA))F(e(t))=

-2eT(t-τ)(IN⊗(DPS(t)H2))F(e(t))=

-2eT(t-τ)(IN⊗(DP))(IN⊗S(t)H2)F(e(t))≤

ε8eT(t-τ)(IN⊗(DPPTD))e(t-τ)+

(23)

-2eT(t-τ)(IN⊗(DB))F(e(t-τ))≤

(24)

-2eT(t-τ)(IN⊗(DΔB))F(e(t-τ))=

-2eT(t-τ)(IN⊗(DPS(t)H3))F(e(t-τ))=

-2eT(t-τ)(IN⊗(DP))(IN⊗(S(t)H3))F(e(t-τ))≤

ε10eT(t-τ)(IN⊗(DPPTD))e(t-τ)+

(25)

将式(16)—(25)代入式(12),可得

2cG⊗Γ+MTM-2R1]e(t)+2eT(t-τ)[IN⊗(DC)-

(ε6+ε8+ε10)DPPTD+ε7DAATD+ε9DBBTD)+NTN-

2(IN⊗D)R2]e(t-τ)-2η|e(t)-(IN⊗D)e(t-τ)|δ+1．

(26)

根据引理2,有

-2η|e(t)-(IN⊗D)e(t-τ)|δ+1=

-2η((De(t))T(De(t)))(δ+1)/2=

-2ηV(δ+1)/2(t)．

(27)

接着对式(10)和(26)求数学期望,可得

(28)

其中

2cG⊗Γ+MTM-2R1,

(ε6+ε8+ε10)DPPTD+ε7DAATD+ε9DBBTD)+NTN-2(IN⊗D)R2,

Ω3=IN⊗(DC)-cG⊗(DΓ)+(IN⊗D)R1+R2．

当定理1成立时,E[dV(t)]≤-2ηE[V(t)](δ+1)/2．通过引理3,可以保证误差系统(4)可以在设定时间T0=V(1-δ)/2(0)/(η(1-δ))实现有限时间同步,证明完成．

控制器算法的步骤如下:

步1 定义激活函数f(·)和Gauss函数的宽度σi,并选择矩阵D,C,B,A,Γ,G;

步2 选择不确定参数矩阵P,H1,H2,H3及噪声强度矩阵M,N;

步3 通过e(t)=y(t)-x(t)计算e(t);

步4 选择合适的参数η>0,0<δ<1,且由式(8)可以确定对称矩阵R1,R2;

步5 计算u(t)的值,并将其用于产生控制信号．

3 仿真

在本节中,我们将通过以下的仿真来检验所设计的反馈控制器的有效性．误差系统(4)的参数设计为

激活函数为f(·)=tanh(·),η=1.13,δ=0.5,x1(0)=[1.2,1.8]T,x2(0)=[1.5,0.8]T,y1(0)=[1.7,-2.3]T,y2(0)=[1.3,0.4]T,τ=0.1．通过使用MATLAB的Yalmip工具箱,求得

ε1=0.316,ε2=0.512,ε3=0.235,ε4=0.613,ε5=2.130,

ε6=0.718,ε7=0.223,ε8=0.313,ε9=0.524,ε10=0.413．

经过检验,以上结果满足假设1、2、3和定理1中的条件．因此误差系统(4)可以实现有限时间同步．通过仿真,可以得到以下仿真结果．图2为随机噪声,图3和图4分别描绘了无控制输入和控制器(5)作用下误差系统(4)的状态曲线,且同步时间t≈3.3 s

图2 随机噪声图3 无控制器作用下的误差系统状态轨迹Fig. 2 Random noisesFig. 3 State trajectories of the error system

图4 控制器(5)作用下的误差系统状态轨迹图5 控制输入Fig. 4 State trajectories of the error system with controller (5) Fig. 5 Control inputs

注3 与文献[17]的同步时间t≈5 s和文献[18]的同步时间t≈10 s相比,本文所设计的控制器可以使系统在t≈3.3 s内达到同步,同步时间更短,更具优越性．

注为了解释图中的颜色,读者可以参考本文的电子网页版本．

4 结论

本文进一步研究了中立型耦合神经网络的有限时间同步问题．所使用的模型同时考虑了时滞、不确定性和随机扰动的影响, 更具普遍性．通过构造合适的Lyapunov函数和运用不等式技术,推导出中立型耦合神经网络的有限时间同步准则．设计适当的状态反馈控制器,使所考虑的系统达到有限时间同步状态．最后通过仿真结果检验了所获结论的有效性．