线性渐进滤光成像高光谱数据的波段配准方法*

于春瑶,方俊永,王潇,张晓红,刘学

(1 中国科学院空天信息创新研究院, 北京 100094; 2 中国科学院大学, 北京 100049)

高光谱数据具有丰富的空间和光谱信息,能以较高的光谱诊断能力对地物目标进行精细化解译,可大大增强地物信息的提取能力,近年来已成为遥感领域的研究热点[1]。

目前高光谱图像传感器中常见的分光方式主要有光栅分光、棱镜分光、可调谐滤光片分光、芯片镀膜等[2]。本文研究的高光谱相机基于线性渐进滤光片实现光谱分光及高光谱数据采集,与常见的衍射分光的推扫型光谱仪的成像方式不同。渐进滤光片型高光谱相机通常适用于固定成像条件、姿态稳定的场景中,搭载于无人机平台的实例尚不多见。本文针对渐进滤光片型高光谱相机姿态变化及各波段非同步获取情况下的配准问题,提出较适合的数据处理流程和方法。首先需要利用与影像获取同步的POS数据对各波段影像进行几何校正。各波段影像数据几何校正完成后,需要对校正后的所有波段影像进行波段配准,这样才可根据需求将各个波段组合成彩色图像来帮助识图。

校正后的高光谱图像波段配准主要用到图像配准算法。图像配准是对具有一定范围的重叠区域的两幅或多幅图像进行配准的过程[3-4]。目前的图像配准算法主要有两种:基于灰度的图像配准算法和基于特征的图像配准算法[5]。其中,基于特征的图像配准算法应用较为广泛,常用的基于特征的图像配准算法有Moravec算法[6]、Harris算法[7]、SUSAN算法[8]、SIFT算法[9]和SURF算法[10]。SIFT算法对两幅图像之间的旋转、平移、尺度缩放等变换具有较强的鲁棒性,应用较为广泛[4]。但SIFT算法对图像之间的灰度差异并不鲁棒,因此在对灰度差异比较明显的图像之间的配准,很多人提出了改进的图像配准算法。龚志成等[11]针对多光谱遥感卫星图像提出一种基于特征点的快速配准方法,在查找的感兴趣区域内利用SIFT算法提取特征。刘畅等[12]针对红外和可见光图像配准,提出一种基于高曲率特征点匹配的图像配准算法。Ma等[13]通过引入新的梯度定义以及增强的特征匹配方法提出PSO-SIFT算法,该算法对图像的灰度变化更加鲁棒。王晶晶等[14]通过设计两组匹配策略实验,提出一种适合框幅式高光谱影像波段配准的匹配策略。本文处理的高光谱数据各波段之间的灰度变化较为明显,而SIFT算法对于图像之间的灰度差异不够鲁棒,因此本文调整了波段配准的策略,并在PSO-SIFT算法[13]的基础上,提出适用于线性渐进滤光成像的高光谱数据波段配准的双充分性SIFT算法(double sufficiency-SIFT,DS-SIFT)。本文将介绍线性渐进滤光成像传感器及其成像原理,波段配准前数据预处理及几何校正,重点探讨DS-SIFT图像配准算法原理与流程,最终根据实验结果进行分析验证。

1 传感器介绍

本文研究的高光谱相机采用的传感器为CMV2K LS150+ VIS-NIR,其基本成像仪类型为CMOSIS CMV2000,属于线性渐进滤光,响应范围为2 048像素×1 088像素,其波长范围为可见光到近红外470～900 nm。图1为本文所研究的传感器的概念图。传感器将高光谱滤光片与标准CMOS图像传感器集成:该传感器去除了笨重的准直仪、棱镜和光栅组件,没有对准问题;由CMOS处理基础和制造基础架构支持,具有高性能、低成本等特点;由于无人机载重有限,因此本传感器在无人机遥感领域具有良好的应用前景。

图1 线性渐进滤光高光谱传感器概念图Fig.1 Conceptual picture of linear progressive filter hyperspectral sensor

为便于说明线性渐进滤光传感器的成像原理,将传统分光方式与线性渐进滤光进一步阐述,在图2中进行对比。图2(a)为传统分光方式成像的相机一次曝光形成的影像,各个波段对应的都是相同地物。图2(b)为基于线性渐进滤光成像的相机3次曝光形成的影像,每次曝光不同波段对应的地物不同。传感器获取数据时每5行对应一个波段,后期为便于处理,将每5行中提取出一行重新组成一个高光谱影像数据进行处理,这里采用的是每5行中提取出第3行组成新的影像。

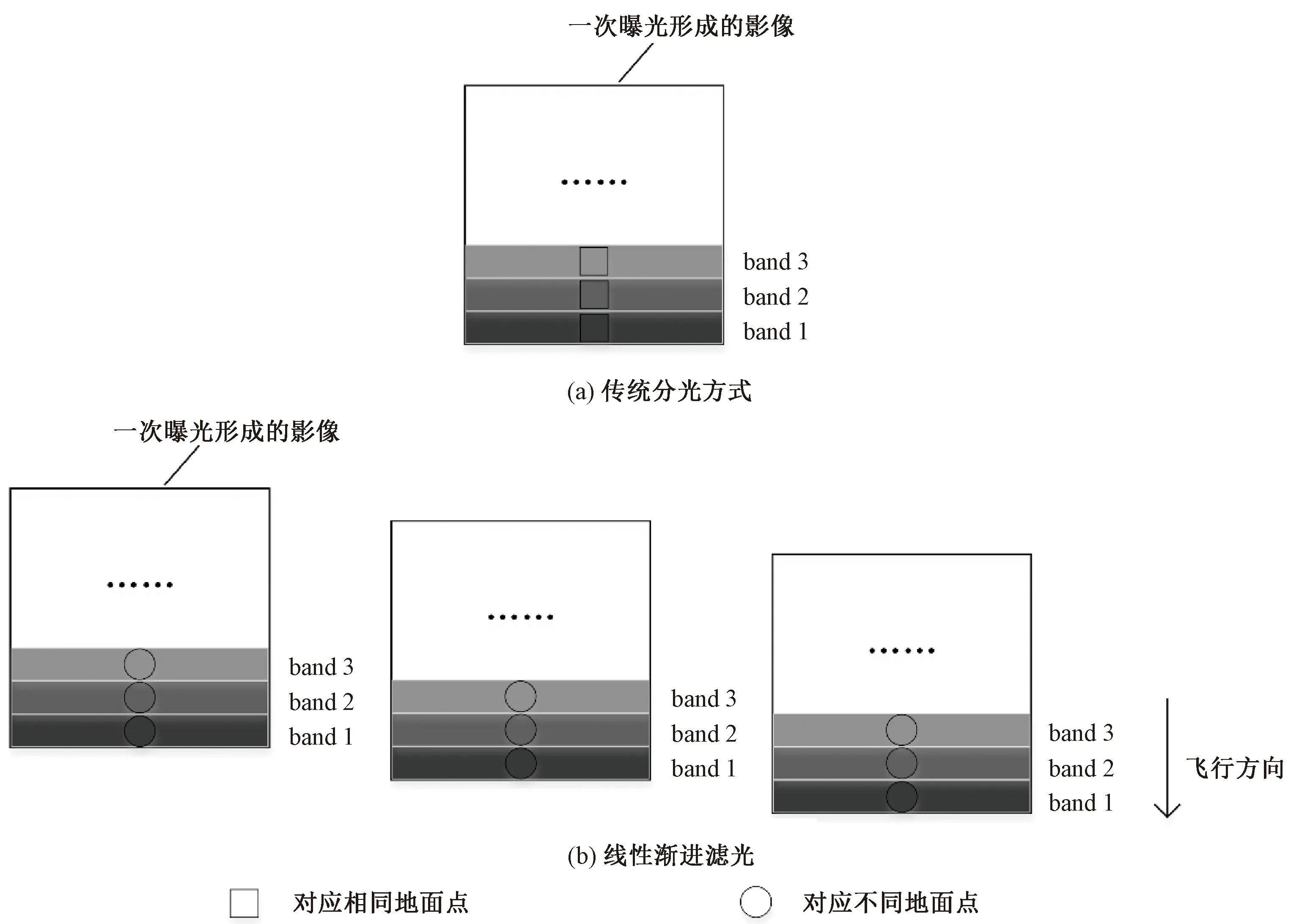
图2 分光方式对比图Fig.2 Comparison of spectroscopic methods

2 几何校正

线性渐进滤光传感器属于线中心投影。无人机飞行过程中易受低空气流影响,飞机姿态不稳定,速度不均匀,导致影像会有较为严重的几何变形[15]。利用POS系统可以获取传感器实时的位置和姿态信息,从而可对影像进行校正。飞行实验后得到的POS数据利用POSPac软件进行处理后可得到姿态角与位置信息。将其进行坐标转换,可得到影像在拍摄瞬间的空间位置和姿态。坐标转换过程如下:像空间坐标系(i)→传感器坐标系(c)→IMU坐标系(b)→导航坐标系(n)→地心地固坐标系(e)→局部空间直角坐标系(m)。其旋转矩阵可表示为

(1)

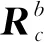
影像外方位线元素的计算方法如下:

(2)

其中:(XIMU,YIMU,ZIMU)e为IMU中心在地心空间直角坐标系下的坐标,(xl,yl,zl)为传感器透视中心在IMU坐标系中的坐标,(X0,Y0,Z0)e为局部空间直角坐标系远点在地心空间直角坐标系中的坐标。

提取单行数据后的线性渐进滤光高光谱影像进行几何校正的原理与以往线阵高光谱影像进行几何校正的原理基本相同,但需注意的是,线性渐进滤光高光谱影像需要各个波段单独进行几何校正,各个波段校正所需的POS数据并不相同。本文利用典型的共线方程法对各个波段进行几何校正,共线方程法中主要有两种校正方法,一种为直接法几何校正,另一种为间接法几何校正。由于直接法几何校正效果较差,校正后的影像会出现重叠或空白,使得原始数据丢失,而间接法的重采样精度较高,光谱保真度高,因此这里采用间接法对高光谱影像进行校正[17]。间接法几何校正采用的共线方程如下:

(3)

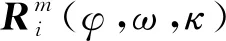
3 波段配准

根据线性渐进滤光传感器获取影像的特点,经几何校正后的高光谱影像需要进行波段配准。由于高光谱影像波段数多,且各波段影像之间的灰度会有明显差异,因此配准后100多个波段上的地物很难一一对应,这也是对本传感器获取的影像进行配准的一个难点。若只是单纯地利用SIFT算法将所有波段影像以某一波段影像为基准进行配准,波段间灰度差异大,而SIFT算法对灰度差异并不鲁棒,配准后的效果较差。因此这里将采用对高光谱各波段影像进行分组,选出3层基准波段,并对分组后的影像利用DS-SIFT算法进行图像配准。其中,分层有助于选出基准波段中效果最优的波段,通过逐层将其他基准波段与最优基准波段进行配准,使得其他基准波段间的差异最小化,从而有助于数据整体的波段配准。

3.1 波段配准策略

3.1.1 波段影像分组并选取基准波段

线性渐进滤光高光谱数据所有波段反映的均为同一区域地物的灰度信息,高光谱数据连续波段图像之间相似性大,非相邻波段间的图像灰度差异较为明显,尤其是可见光与近红外谱段的图像灰度差异很大,甚至会出现同一地物灰度相反的情况,因此在配准过程中基准波段的选取将会对配准效果产生较大的影响。为取得最佳的配准效果需要兼顾多个波段之间的灰度联系,因此提出按照分组计算互信息,并取交点波段作为选取基准波段的方法。互信息表示一个图像中包含另外一个图像的信息量,若两个图像越相似,互信息也就越大。计算波段之间的互信息,并将所有互信息数据绘制成图,将图像交点按照就近原则取整即选出交点波段。对各个波段图像进行配准前,首先剔除效果较差的波段,避免个别质量较差的波段影响整体的配准效果,然后进行初步分组选取基准波段。

初步分组的原则是根据实际数据的灰度变化情况将波段按照顺序进行均匀分组,每组的波段数相同。考虑到需要选取交点波段作为基准波段,需保证每两组数据之间都有相同数量的重叠波段,组内前半部分波段与前一组重叠,组内后半部分波段与后一组重叠。在上述分组中,存在第1组的前半部分无交点,所以将第1组的前半部分波段再划分为一组,记为pre1组,与第1组的前半部分重叠。同理,最后1组的后半部分划分为一组,记为post1组,与最后1组的后半部分重叠。以本文数据为例,剔除瑕疵波段后共有128个波段,数据初步分组数为17,分组情况如图3所示。本文采用选取3层基准波段并逐层返回配准的方式。其中,第1层基准波段的选取过程如下:

1)将剔除瑕疵波段后的所有波段数据进行初步分组,每组的初始基准波段选取位于组内最中间位置的波段,其中,pre1组和post1组分别以第1个、最后1个波段为初始基准波段;

2)选取好初始基准波段后,利用SIFT算法将每个波段以组内的初始基准波段为基准进行配准,并计算互信息;

3)将所有计算好的互信息描点画图,根据就近原则选取交点波段作为第1层基准波段。

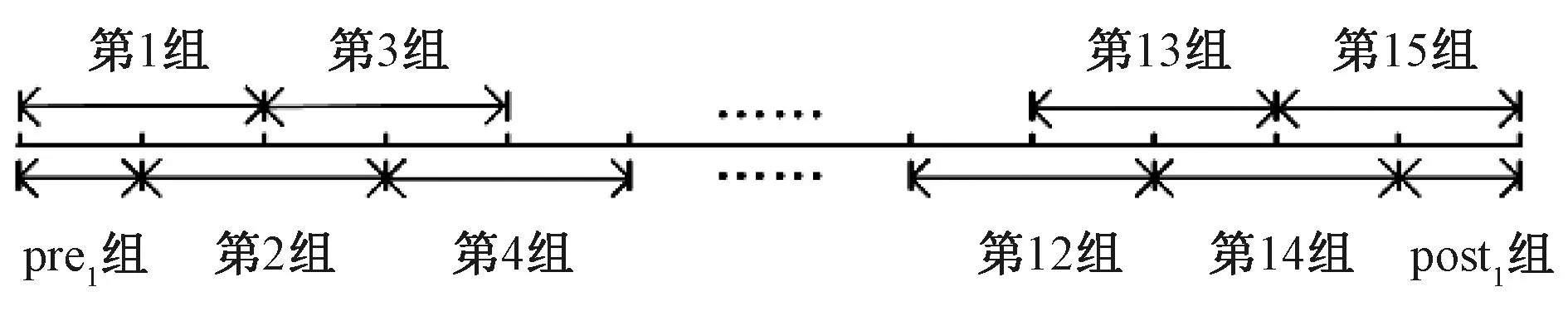
图3 初始分组图Fig.3 Initial grouping graph

以所有第1层基准波段作为第2层选取基准波段的初始数据,按照与第1层相同的原理,第2层分组数为3,按照顺序分别为pre2组、所有第1层基准波段组成的一组、post2组。最终从第1层基准波段中选取出2个第2层基准波段。随后2个第2层基准波段相互配准并计算互信息,比较以哪个波段作为基准计算出的互信息最大,以此选出一个第3层基准波段。

3.1.2 分组逐层返回配准

在选好3层基准波段后,开始对图像采取逐层返回的方式利用DS-SIFT算法进行配准。分组逐层返回配准的具体步骤如下:

1)以第3层基准波段为基准,将第2层基准波段中的另一个波段进行配准。

2)配准后的第2层基准波段作为第1层基准波段的基准,第1层的所有基准波段按照顺序均匀地分组,此时的分组之间不需要有重叠,以本文实验为例,第1层基准波段共有16个,以8个为一组分为2组,前1组以第2层基准波段中的前一个波段为基准进行配准,另1组以后一个波段为基准波段进行配准。

3)配准好的第1层基准波段作为基准,配准原图像,也是按照顺序均匀分组后进行配准。

3.2 DS-SIFT算法

SIFT算法为图像配准算法中的经典算法,它使用高斯差分金字塔来检测关键点,具有尺度不变性,且在平移、旋转、亮度变换保持不变形等方面具有鲁棒性[5,18]。但SIFT算法对于灰度差异明显的图像之间的配准并不鲁棒,因此本文提出双充分性SIFT算法——DS-SIFT算法对灰度变化明显的高光谱数据进行波段配准。DS-SIFT算法主要分为粗配准和精配准两部分进行,其中粗配准为利用SIFT算法进行配准,精配准为利用PSO-SIFT算法[13]进行配准,但考虑到PSO-SIFT算法所需运行时间较长,且存在部分区域配准效果差的特点,因此在PSO-SIFT算法中引入分块思想和结构相似性,提高了运行效率和配准精度。

1)PSO-SIFT算法

PSO-SIFT算法[13]提出新的梯度定义来克服图像对之间的灰度差异,通过使用原始输入图像构建最低级别的高斯金字塔,利用Sobel滤波器计算尺度空间的梯度幅度,使用类似于GLOH[19-20]的圆形邻域和对数极扇区来创建特征点描述符,梯度方向被划分为8个方向,共有136维的特征描述符;引入通过组合关键点的位置比例及方向来增强图像特征的匹配方法,这样可以增加正确匹配点的数量。

2)图像区域分块方法

考虑到高光谱数据波段数多,数据量大,需要提升算法的运行速度,因此在算法中引入分块思想。在保证粗配准精度的情况下,对PSO-SIFT算法损失少量精度,从而将整个算法的运行速度提升。将图像划分为5×5的子块,只对符合条件的子块进行特征点检测可以有效缩小检测范围,提高算法效率。高光谱影像多个波段进行配准容易出现部分区域配准效果好,而某些区域配准效果差的情况。根据以上两点,在图像粗配准的基础上,对图像进行分块,寻找特征较强但配准效果差的子块进行精配准。文献[21]提出一种基于图像区域分块的SIFT快速配准方法,但对于本文实验数据来说,此方法只能查找到特征丰富的子块,并不能改善图像部分区域配准效果差的问题。因此,不同于文献[21]所提出的区域分块方法,本文提出的分块方法不仅使用信息熵一个指标,通过引入结构相似性(SSIM)来查找配准效果差的子块,保证查找到的子块不仅纹理信息丰富,特征点较多,并且是配准效果差的子块,可以改善图像部分区域重影问题。SSIM是一种衡量两幅图像相似度的指标,其计算公式如下

(4)

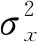
综合上述内容,本文采用的DS-SIFT算法具体步骤如下:

1)首先利用SIFT算法将待配准波段与基准波段进行粗配准,将粗配准后的波段与基准波段均匀地划分为5×5的子块,若边界无法被整除,可对边界部分像素重复计算。

2)计算经粗配准后波段的各子块与基准波段相应子块的SSIM和信息熵;

3)将每个子块的SSIM及信息熵与阈值进行比较,本文设置的SSIM阈值为0.7,信息熵阈值为6。将SSIM小于0.7且信息熵大于6的区域作为待检测区域。

4)对第3)步计算出的待检测区域以基准波段的相应子块为基准利用PSO-SIFT算法检测特征点并计算变换矩阵,其他区域不进行检测;

5)利用计算出的变换矩阵将粗配准后的波段进行精配准。

基于文献[21]的研究以及经过大量数据实验,本文精配准中信息熵的阈值为6,SSIM的阈值为0.7。2个参数阈值的确定主要是根据图像的信息量以及两图像之间的相似性确定的。若图像越平坦,信息熵的阈值要降低;两图像越相似,SSIM的阈值要增加。

4 实验结果及分析

正如第1节所介绍的,实验所用的高光谱相机采用的传感器属于线性渐进滤光,实验数据为2019年10月25日于天津飞行的数据。由于数据前64个波段质量较差,故从第65波段开始选取数据,到第192波段结束,共计128个波段。在下面叙述中,将第65波段按照第1波段进行叙述,剩下的波段以此类推,第192波段叙述为第128波段。

4.1 几何校正

渐进滤光型高光谱相机获得的原始影像数据如图4(a),这里以一个波段显示,可以看到原始影像上的地物尺寸比例与现实不符,很难分辨出地物。每5行提取1行数据后组成的未校正图像如图4(b),可以看到重新提取后的数据的可判读性有了很大的提升,但是地物仍存在扭曲、变形,且地物的方位与真实情况不符,使得对图像的判读仍受影响。对其进行几何校正后的图像如图4(c)所示,可以看到,原来扭曲的地物经几何校正后被较好地还原,地物恢复了原有的方位和形状,从局部细节放大图中可以看到道路和桥梁的线条流畅明朗,绿化区树木形状规则,说明几何校正效果较好。

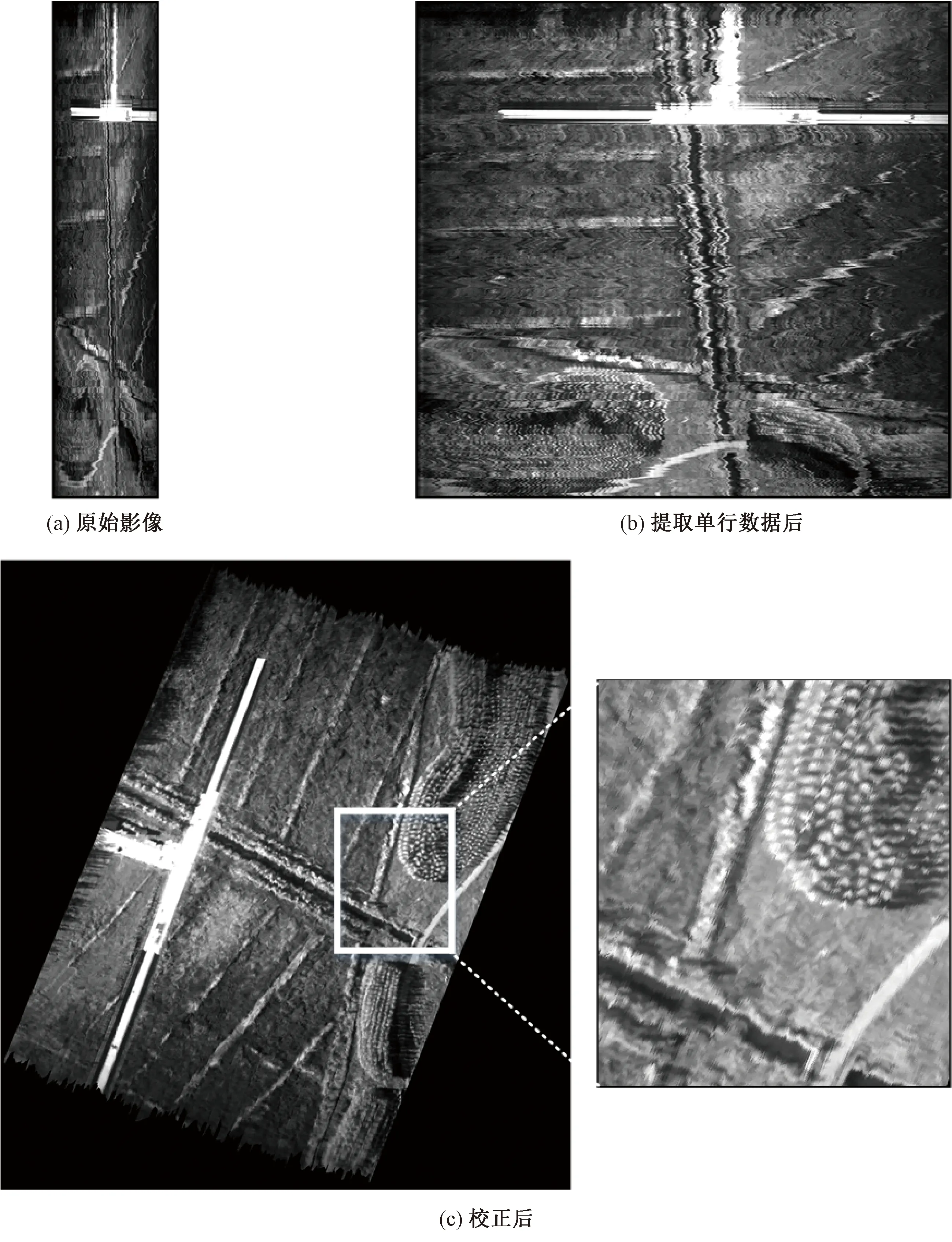
图4 线性渐进滤光成像的原始图像及校正前后对比(以波段36显示)Fig.4 Original image of linear progressive filter imaging and comparison before and after correction (band 36)

4.2 基准波段选择

经几何校正后,要对高光谱数据进行波段配准,首先选取基准波段。在3.1节的对128个波段进行初始分组之上,画出互信息图,如图5(a)所示,可以得到基准波段序号为4、12、20、29、36、43、52、59、68、75、83、93、101、107、116、123,以上波段作为第1层基准波段;对第1层基准波段画出互信息图,如图5(b)所示,可得到第2层基准波段序号为36、101;接着对第2层基准波段进行互信息的对比,可得到第3层基准波段序号为36。

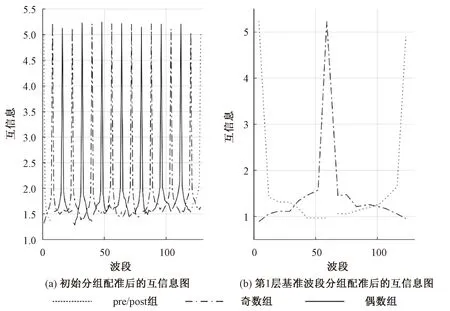
图5 初始分组配准后互信息图Fig.5 Mutual information map after initial grouping registration

4.3 图像配准结果评价

为证明本文算法的优越性,设置3组实验,其中第1组为几何精度验证实验,其余2组为互信息对比实验和时间优越性对比实验。

1)几何精度验证实验

为评价经DS-SIFT算法配准后的图像几何精度,利用均方根误差进行验证,图6为经DS-SIFT算法精配准后的均方根误差,可以看到误差已达到亚像元精度。

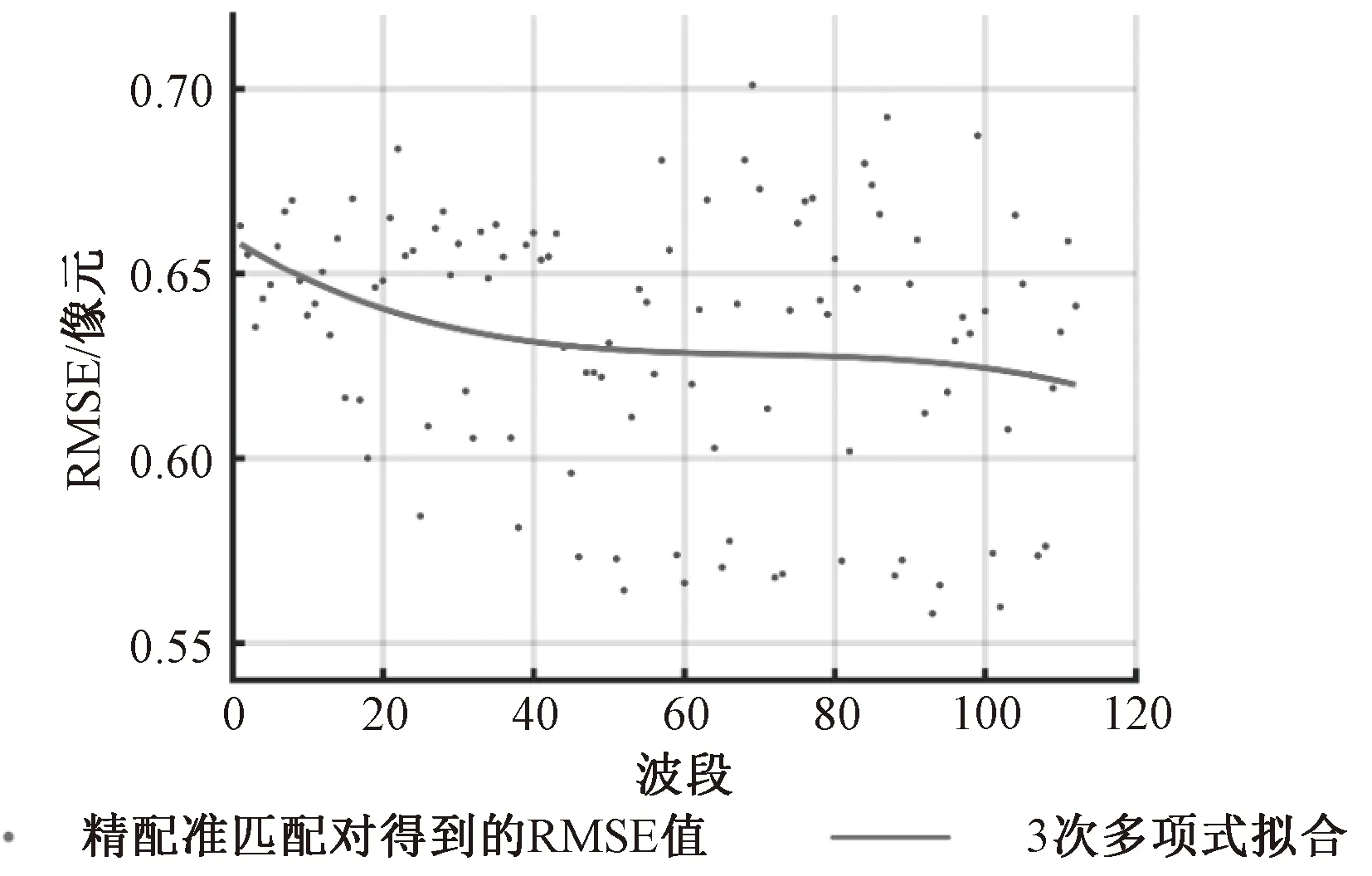
图6 均方根误差图Fig.6 Root mean square error plot

2)互信息对比实验

为验证DS-SIFT算法所带来的精度上的提升,将只对图像利用SIFT算法进行配准作为对比实验。采用互信息作为衡量配准后精度对比的指标,互信息计算公式为

(5)

其中:X,Y表示图像,x,y表示图像的像素,p(x,y)表示联合概率,p(x)和p(y)表示单个像素在图像中的概率。图7(a)为DS-SIFT算法和SIFT算法实验后得到的112个非基准波段的与配准之前互信息相减的差值图,可以看到数值均大于0。因此,相比于SIFT算法,经DS-SIFT算法配准后的波段之间的互信息更大,证明DS-SIFT算法的图像配准效果更好。

3)时间优越性对比实验

为证明本文提出的分块思想所带来的运行速度上的改进,同样利用SIFT算法进行粗配准,利用未分块的改进SIFT算法进行精配准,与本文提出的DS-SIFT算法进行对比实验,实验运行所需时间如图7(b)所示。可以看到,通过引入分块思想后,本文提出的算法加快了图像配准的运行速度。

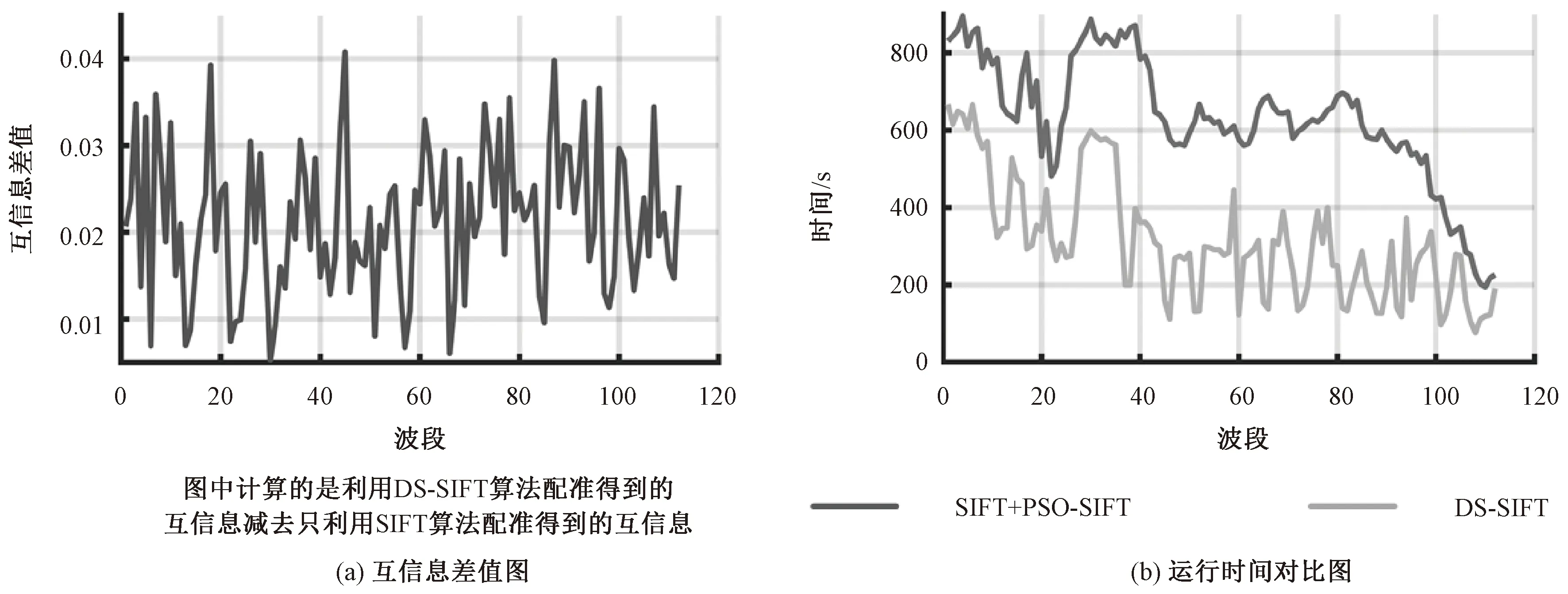
图7 2组对比实验结果图Fig.7 Comparison of the results of the two groups of experiments

图8 图像配准后结果图Fig.8 Result image after image registration

从上述2组对比实验可以看出,本文提出的DS-SIFT算法的精度要优于SIFT算法。在配准运行速度上,本文提出的算法相对于SIFT算法+PSO-SIFT算法的结合上有了很大改善,在保证精度的情况下使得运行速度有了提升。图8为最终波段配准后的结果图,这里随机选取3个波段进行合成,可以看到最终配准的效果较好,由于传感器性质导致图像内部会出现一些轻微重影。对于同一位置的地物,各波段获取的时间不一致,若为边界不明确或易受外界影响的地物,其在各波段上的成像极可能不完全一致,即使经过配准仍存在差异。对于边缘的重影部分,主要是由于经几何校正后每个波段的大小和边界都不相同。综上,DS-SIFT算法更适用于波段数量多、数据量大的高光谱数据的配准。

5 结论

本文研究基于线性渐进滤光成像的高光谱数据的波段配准方法。基于该传感器的成像特性,首先对各波段进行逐行几何校正,随后提出一种分组逐层返回配准的波段配准策略和DS-SIFT算法。首先利用信息熵交叉,得到基准波段;其次利用DS-SIFT算法进行波段配准,利用新的梯度定义适应图像对之间的灰度差异提高配准精度,利用信息熵和SSIM的阈值条件进行精配准之间配准矩阵的求解。实验结果表明,本文提出的DS-SIFT算法配准效率较高,算法整体精度优于SIFT算法。未来在进行相关实验时会在地面布设控制点,从而可对该图像配准算法进行进一步的精度验证。