基于谐波合成法模拟的脉动风速功率谱密度和相关性分析

张慧彬

（华杰工程咨询有限公司，北京 100029）

0 引言

近年来，我国对基础设施建设持续投入，跨越江河、海洋、峡谷的大跨度桥梁应用广泛。为满足通航需求，大跨度桥梁通常一跨或几跨跨越江河，主跨跨径已达千米级别，如主跨1018m 的香港昂船洲大桥，主跨1088m 的苏通长江公路大桥，沪苏通长江公铁大桥以及在建的常泰长江公铁大桥。大跨度桥梁主跨跨径增加、结构刚度变小、对风的敏感性增加，表现出轻、柔、高的特征。江河、海洋、峡谷地区风环境复杂，风荷载很容易引起桥梁较大的变形和振动，影响结构的可靠性和安全性。在进行时域风振响应分析时，风荷载已经成为大跨度桥梁结构设计的控制性荷载。因此，模拟桥梁结构的风荷载，进而对桥梁进行风致振动响应分析是大跨度桥梁设计中必须考虑的重要因素。

众多学者首先采用现场的风场实测或健康监测的方法，获取桥址区和桥梁结构自然风场的特性。一方面采集的风特性实测数据可以用于脉动风场数值模拟，另一方面可用于桥梁结构风洞试验。针对不同地区的气候特征、地形条件等因素，不同国家和地区制定了相应的规范，如美国建筑荷载规范（ASCE7-10）、加拿大国家建筑规范（NBCC）等。针对复杂地区的大跨度桥梁的风场特性分析，众多学者往往进行现场监测，补充桥梁结构所受来流风的实测数据。例如，王浩等[1]针对润扬大桥和苏通大桥的健康监测平台，采集了特殊气候条件下桥址区的风场特性；赵林等[2]利用台风经过西堠门大桥时的实测数据，分析了湍流强度和功率谱特性。

基于实测风场特性的分析结果，采用线性滤波法、谐波合成法和小波变换等方法，模拟桥梁结构的来流风，成为时域分析中的常用分析办法。例如，王浩等[3]基于润扬悬索桥的实测数据，对桥址区三维脉动风场进行了有效的数值模拟；宋玉鹏等[4]采用二维波数-频率域的非均匀离散策略，改善了谐波合成法的计算效率；李黎等[5]考虑了桥塔风效应，有效模拟了龙潭河特大桥施工最大双悬臂阶段的脉动风场；马俊等[6]结合谐波合成法和自回归方法的优点，提出高效高精度新型混合方法，计算精度显著提高；韩艳和陈政清[7]根据文献的数值方法，模拟洞庭湖大桥脉动风场；孙芳锦和顾明[8]应用小波分解方法，结合线性滤波法的向量过程自回归模型，给出了模拟空间脉动风场的一种新方法。

以规范幂指数、风速谱和相干函数为输入条件，采用谐波合成法数值模拟大跨度桥梁主梁位置处的脉动风速，对模拟的风速时程分析了功率谱特性，表明该模拟方法可以有效模拟桥梁结构所承受的来流风。

1 风速模拟

1.1 模拟参数

1.1.1 对数律

在一段具有均匀粗糙度的水平场地内，对数律可以较为准确地描述大气边界层100～200m 高度范围内的平均风速。平均风速沿高度变化规律可以用式（1）来描述：

式（1）中：z为高度；k为冯卡门常数，一般取值为0.4；U*为地表摩擦速度或流动剪切速度；z0为气动粗糙长度。

1.1.2 脉动风速谱

脉动风速谱反映了不同频率成分的涡对总能量的贡献，湍流运动能量从低频大涡逐渐传递到高频小涡。含有湍流绝大部分能量的大尺度涡范围称为含能尺度，湍流能耗散的小尺度涡范围称为耗散尺度，在远离含能尺度和耗散尺度的中间区域称为惯性子区。在风工程领域，应用较广的经验公式Kaimal 脉动风速谱表达式（2）如下：

Panofsky 脉动风速谱表达式（3）为：

横风向脉动风速谱表达式（4）为：

式（2）～式（4）中：x = nz/U(z)。Kaimal 脉动风速谱反映了高度对风谱的影响。横风向脉动风速功率谱相对于顺风向谱，谱值相对较小，因此在风振响应分析中一般应用较少。

在我国规范[9]中，顺风向和竖向脉动风速谱采用如公式（5）所示：

式（5）中：U为平均风速；n为频率；z为高度；Su和Sw分别为顺风向和竖向脉动风速谱函数；u*为摩擦速度。采用我国规范推荐的公式进行计算分析。

1.1.3 相干函数

空间两点的脉动风速相关性在频域中用相干函数来表示。Davenport 相干函数经验表达式为[10]：

其中：

式（6）～式（8）中：r为p1和p2两点间的距离；Coh(r,n)为相干函数（平方根）。Cy=16 和Cz=10。

式6 中的相干函数与频率有关，改进后的经验公式（9）如下：

式（9）中：Δ 为空间两点的距离；B为调整系数；U为两点的平均风速均值；C为指数衰减系数。

1.2 谐波合成法

基于上述参数，模拟作用全桥各个离散点的脉动风速时程。脉动风速时程近似为一个零均值多变量一维平稳随机过程，可以用式（10）进行模拟：

式（10）中：Δn = fs/N,fs为截止频率，N为数据长度；m为空间点数；M为离散频率点数，满足N≥2M；ψkl为均匀分布于[0,2π)区间的随机相位。

ωkl为双索引圆频率，Δω=2π×Δn，其定义为：

Hjk(wkl)为m点空间脉动风互谱矩阵S(wl)的Cholesky 分解矩阵：

θjk为Hjk(wkl)的相位，即

1.3 风速模拟算例

首先对全桥三维脉动风速场进行简化。模拟计算的主要参数和结果如下：主梁离地高度z=70m；模拟点数n=80；间距为28m。采样频率fs=10Hz；样本时间间隔△t=0.1s；模拟频率分量总数为3000。

主梁跨中模拟点的脉动风速时程曲线如图1所示。

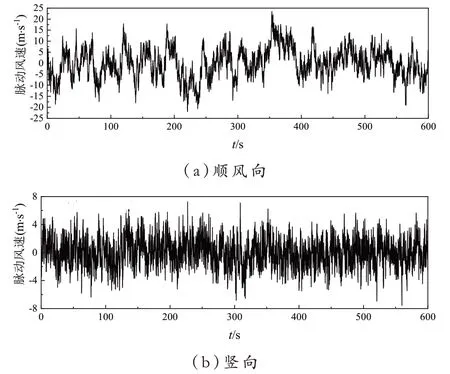
图1 主梁脉动风速时程

为了检验上述模拟点计算结果的可靠性，对脉动风速谱和相关函数进行验证分析。基于生成的风速样本，估计了主梁模拟点自功率谱，并与目标谱进行了比较。

主梁跨中脉动风速谱和目标谱如图2所示。对于顺风向脉动风速谱，在0.001～0.01Hz 低频段内模拟的脉动风速谱值较目标谱值低；在0.01～0.1Hz 频段内，略高于目标谱值；在0.09Hz 存在极小值，之后随着频率增大，模拟的谱值在目标谱上下波动。对于竖向脉动风速谱，在0.001～0.01Hz 低频段内模拟的脉动风速谱值较目标谱值低；在0.01～0.1Hz 频段内低于目标谱值；在0.05Hz 存在极小值，之后随着频率增大，模拟的谱值在目标谱上下波动。整体上看，模拟曲线在目标函数曲线上下波动，其模拟谱与目标谱均吻合较好，验证了模拟方法的有效性和可靠性，表明模拟结果合理。对于顺风向和竖向，主跨跨中模拟点在低频段顺风向谱密度明显大于竖向，在高频段谱密度均波动明显。

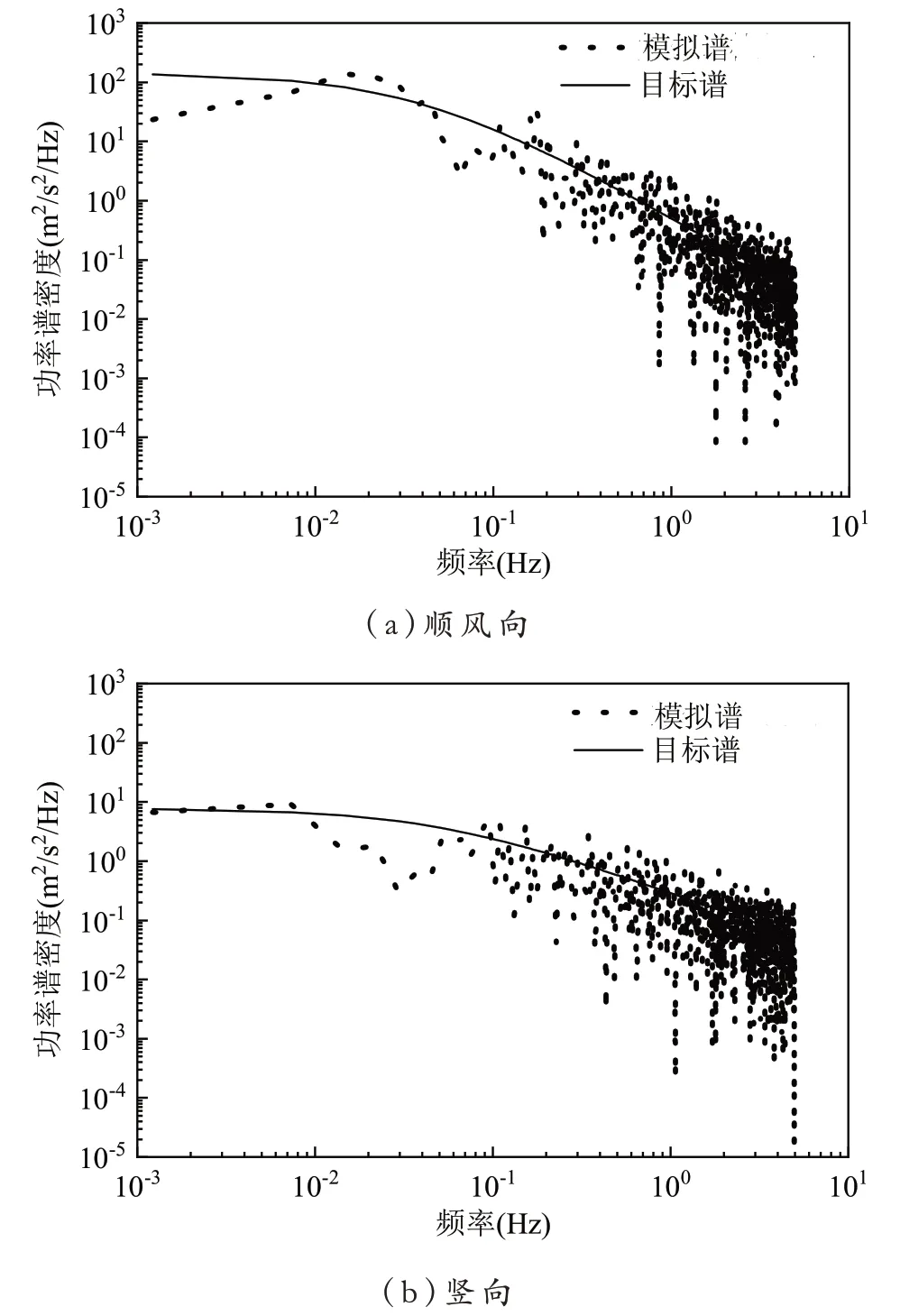
图2 主梁模拟脉动风速功率谱密度

无论是顺风向还是竖向脉动风速功率谱，均显示出低频（大涡）湍流脉动能量较大，谱值较高；在高频（小涡）段，脉动能量较小，谱值较低。这也符合脉动风在大尺度涡范围内，气流惯性力起主导作用，在惯性力作用下，能量从大涡传递到小涡，再由小涡传递到更小尺度的涡，湍流运动能逐渐被耗散成内能。

2 结语

其一，基于谐波合成法模拟不同位置处的脉动风速时程。以规范推荐值为输入参数，模拟得出主梁跨中顺风向脉动风速在25m/s 范围内波动，竖向脉动风速在8m/s 范围内波动。

其二，通过检验样本时程风速谱，对于顺风向脉动风速谱，在0.001～0.01Hz 低频段内模拟的脉动风速谱值较目标谱值低，在0.01～0.1Hz 频段内略高；对于竖风向脉动风速谱，在0.001～0.01Hz 低频段内模拟的脉动风速谱值与目标值相符，在0.01～0.1Hz频段内低于目标谱值。整体上，风速谱模拟曲线在目标函数曲线上下波动，其模拟谱与目标谱均吻合较好，验证了模拟方法的有效性和可靠性。