动态问题中的函数图象

薛丽

在求解动态问题中的函数图象相关问题的过程中，数形结合思想的运用至关重要.同学们要能根据函数图象的性质和图象上的数据分析得出函数的变化趋势，结合实际情况求解.

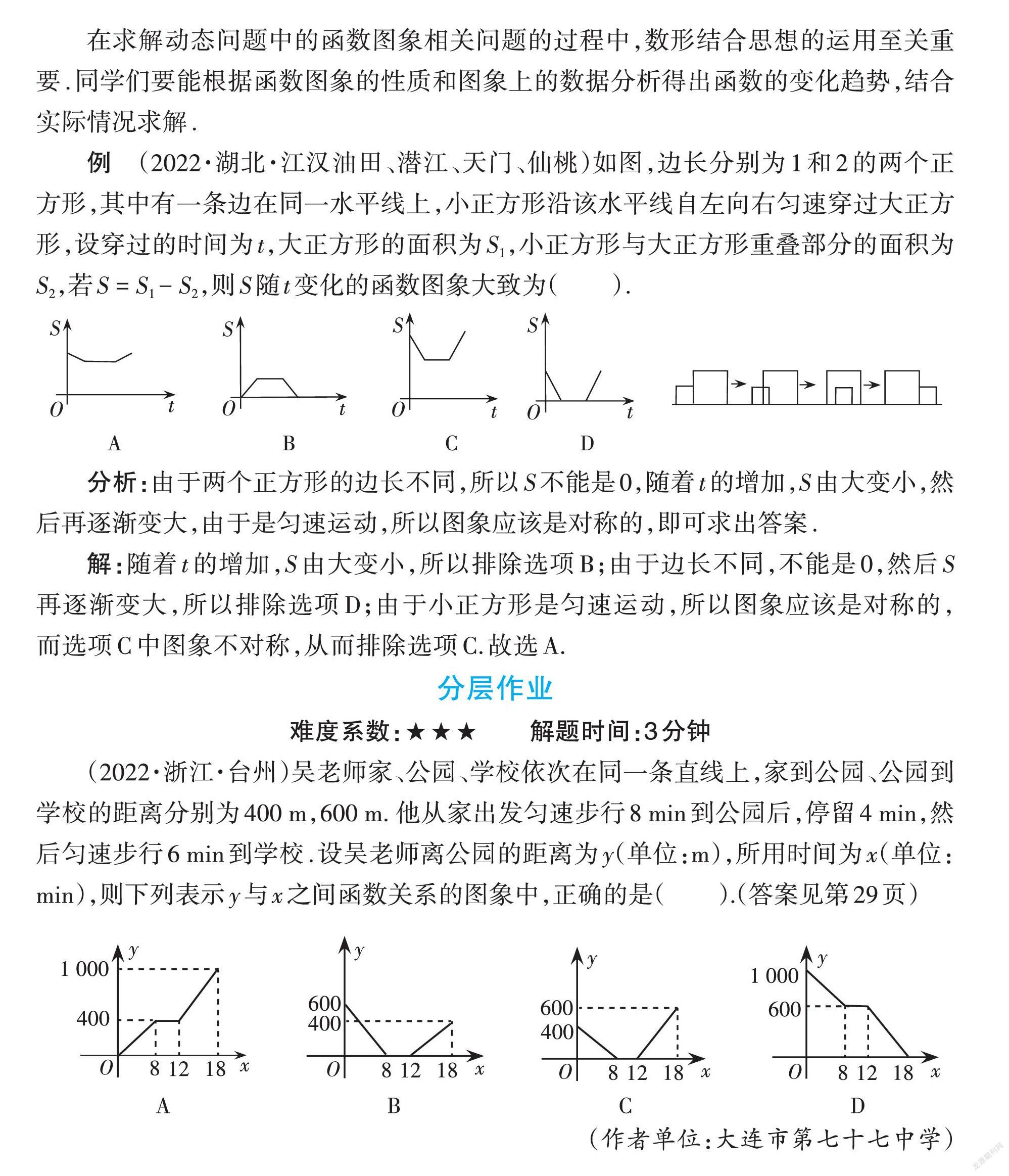
例 （2022·湖北·江汉油田、潜江、天门、仙桃）如图，边长分别为1和2的两个正方形，其中有一条边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t，大正方形的面积为S1，小正方形与大正方形重叠部分的面积为S2，若S = S1 - S2，则S随t变化的函数图象大致为（ ）．

分析：由于两个正方形的边长不同，所以S不能是0，随着t的增加，S由大变小，然后再逐渐变大，由于是匀速运动，所以图象应该是对称的，即可求出答案.

解：随着t的增加，S由大变小，所以排除选项B；由于边长不同，不能是0，然后S再逐渐变大，所以排除选项D；由于小正方形是匀速运动，所以图象应该是对称的，而选项C中图象不对称，从而排除选项C.故选A.

分层作业

難度系数：★★★ 解题时间：3分钟

（2022·浙江·台州）吴老师家、公园、学校依次在同一条直线上，家到公园、公园到学校的距离分别为400 m，600 m. 他从家出发匀速步行8 min到公园后，停留4 min，然后匀速步行6 min到学校.设吴老师离公园的距离为y（单位：m），所用时间为x（单位：min），则下列表示y与x之间函数关系的图象中，正确的是（ ）.（答案见第29页）

（作者单位：大连市第七十七中学）