这两道题很难吗

雷添淇

本栏目试题选自全国中小学数学创新应用大赛初赛、复赛试卷，由全国中小学数学创新应用大赛组委会供稿.

真题呈现

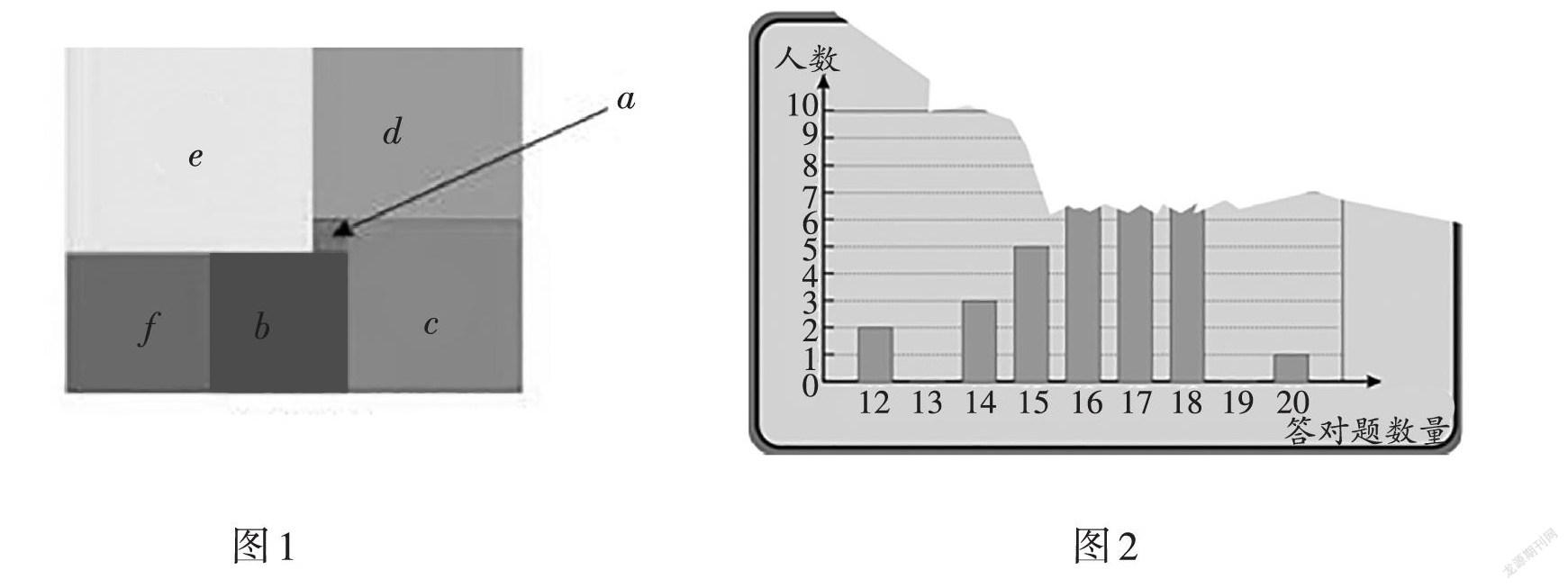
试题1 一个长方形如图1所示，恰分成六个正方形，已知下列（ ）条件，无法求得这个长方形的面积.

A. 已知a的面积            B. 已知b的周长            C. 已知c与d的面积差

D. 已知e与c的边长差      E. 已知e的面积

试题2 中位数是指将数据按大小顺序排列起来，形成一个数列，居于数列中间位置的那个数据，如图2，为某班35名学生参加数学创新应用大赛答对题目数量的条形图. 现条形图被部分损坏导致统计数据不完全，已知最少的答对了12题，最多的答对了20题，答对题目数量的中位数是17. 根据统计图，可以确定的有 .

①答对16题以下的人数    ②答对16题的人数      ③答对17题以下的人数

④答对17题的人数        ⑤ 答对18题的人数      ⑥答对19题以下的人数

试题1 设图1中正方形a，b，c，d，e，f 对应的边长分别为la，lb，lc，ld，le，lf，

由图1可得到如下关系：

[lb+la=lc，①lc+la=ld，②ld+la=le，③lb=lf ，④lb+lf-la=le，⑤][⇒][由①+②+③，得lb+3la=le.⑥将④代入⑤，得2lb-la=le.⑦][⇒][将⑥与⑦联立，  解得lb=4la.]

[⇒]求得[lb=4la，lc=5la，ld=6la，le=7la，lf=4la.]若已知正方形[a]的边长，则其他所有正方形的边长均可求出.

已知任意一个正方形的边长，则其他所有正方形的边长也均可求出.

由选项A，可求出a的边长；由选项B，可求出b的边长；

由选项D，可求出a的边长；由选项E，可求出e的边长；

只有选项C，无法求出任何一个正方形的边长. 故选C.

试题2 根据题意，可得表1，

设答对16题对应[x]人，

答对17题对应[y]人，

答对18题对应[z]人，x，y，z都大于6，

则[x+y+z+11=35]，

即[x+y+z=24] （人）.

（1）根据表1，答对16题以下的为2 + 0 + 3 + 5 = 10（人），则①可确定.

（2）因为全班一共35人，所以答对19题以下的为34人，则⑥可确定.

（3）因为答对题目数量的中位数是17，所以[10+x≤17]，则[x≤7]. 又因为[x>6]，[x]為整数，所以[x=7]，则②可确定.

（4）根据（1）与（3）可知，答对17题以下的人数为10 + 7 = 17（人），则③可确定.

（5）因为[x+y+z=24]，所以[y+z=17]，且[y+z>12]，

则[y=7，z=10]或[y=8，z=9]或[y=9，z=8]或[y=10，z=7.]

故④和⑤无法确定.

综上，根据图2，可以确定的有①②③⑥.  故填①②③⑥.