二倍角解题策略

夏明

大连嘉汇中学王超老师的直播课《二倍角问题解决策略探究》，选自辽宁教育学院“学到汇”公众服务平台“辽宁省初中数学学科周末名师公益课堂”，旨在贯彻落实国家“双减”政策，帮助广大师生自主学习和个性化提升。

王超老师的这节课重点在于把二倍角的条件转化成等角，进而用相似或勾股定理解决问题. 对于刚学完人教版八年级上册教材的同学们来说，将二倍角转化成等角，可为证明三角形全等提供条件.

基本模型

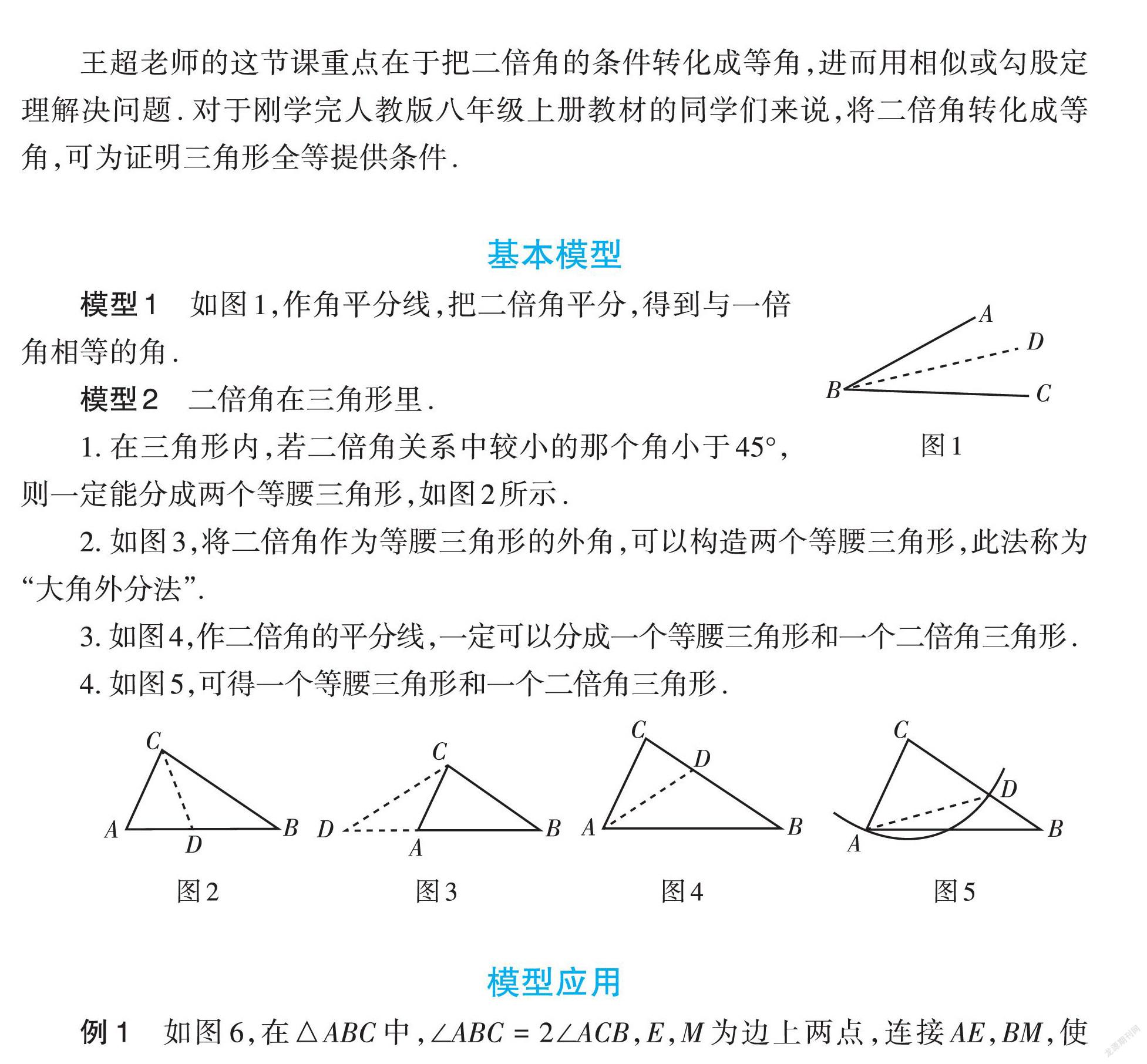
模型1 如图1，作角平分线，把二倍角平分，得到与一倍角相等的角.

模型2 二倍角在三角形里.

1. 在三角形内，若二倍角关系中较小的那个角小于[45°]，则一定能分成两个等腰三角形，如圖2所示.

2. 如图3，将二倍角作为等腰三角形的外角，可以构造两个等腰三角形，此法称为“大角外分法”.

3. 如图4，作二倍角的平分线，一定可以分成一个等腰三角形和一个二倍角三角形.

4. 如图5，可得一个等腰三角形和一个二倍角三角形.

模型应用

例1 如图6，在△ABC中，∠ABC = 2∠ACB，E，M为边上两点，连接AE，BM，使∠BNE = ∠ABC，作∠MFC = ∠AEB，若BC = AB，试判断BE，CF的数量关系并证明.

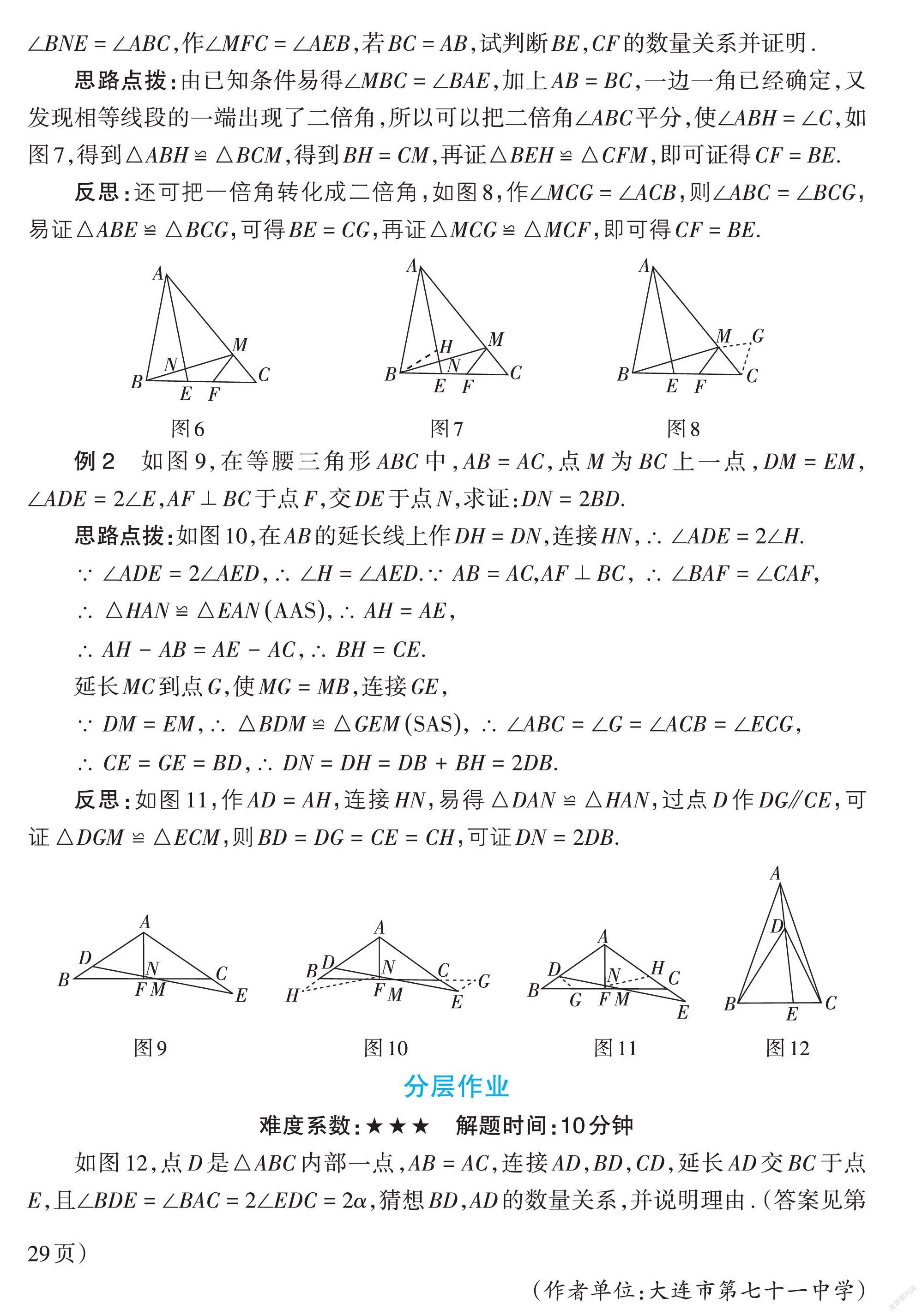
思路点拨：由已知条件易得∠MBC = ∠BAE，加上AB = BC，一边一角已经确定，又发现相等线段的一端出现了二倍角，所以可以把二倍角∠ABC平分，使∠ABH = ∠C，如图7，得到△ABH ≌ △BCM，得到BH = CM，再证△BEH ≌ △CFM，即可证得CF = BE.

反思：还可把一倍角转化成二倍角，如图8，作∠MCG = ∠ACB，则∠ABC = ∠BCG，易证△ABE ≌ △BCG，可得BE = CG，再证△MCG ≌ △MCF，即可得CF = BE.

例2 如图9，在等腰三角形[ABC]中，[AB=AC]，点[M]为[BC]上一点，[DM=EM]，[∠ADE=2∠E]，[AF⊥BC]于点[F]，交[DE]于点[N]，求证：[DN=2BD].

思路点拨：如图10，在AB的延长线上作[DH=DN]，连接HN，[∴∠ADE=2∠H].

[∵∠ADE=2∠AED]，[∴∠H=∠AED].[∵AB=AC，AF⊥BC]， [∴∠BAF=∠CAF，]

[∴△HAN≌△EANAAS]，[∴AH=AE]，

[∴AH-AB=AE-AC]，[∴BH=CE].

延长[MC]到点[G]，使[MG=MB]，连接GE，

[∵DM=EM]，[∴△BDM≌△GEMSAS]， [∴∠ABC=∠G=∠ACB=∠ECG]，

[∴CE=GE=BD]，[∴DN=DH=DB+BH=2DB].

反思：如图11，作[AD=AH]，连接HN，易得[△DAN ≌△HAN]，过点[D]作DG[⫽]CE，可证[△DGM ≌△ECM]，则[BD=DG=CE=CH]，可证[DN=2DB].  [M]

难度系数：★★★ 解题时间：10分钟

如图12，点D是△ABC内部一点，AB = AC，连接AD，BD，CD，延长AD交BC于点E，且∠BDE = ∠BAC = 2∠EDC = 2α，猜想BD，AD的数量关系，并说明理由. （答案见第29页）

（作者单位：大连市第七十一中学）